Determinação das Forças de Impacto em uma Placa Plana com o Método do Volume de Controle

Fonte: Ricardo Mejia-Alvarez e Hussam Hikmat Jabbar, Departamento de Engenharia Mecânica, Michigan State University, East Lansing, MI

O objetivo deste experimento é demonstrar forças nos corpos como resultado de mudanças no impulso linear do fluxo ao seu redor usando uma formulação de volume de controle [1, 2]. A análise do volume de controle se concentra no efeito macroscópico do fluxo nos sistemas de engenharia, em vez da descrição detalhada que poderia ser alcançada com uma análise diferencial. Cada uma dessas duas técnicas tem um lugar na caixa de ferramentas de um analista de engenharia, e devem ser consideradas abordagens complementares e não concorrentes. Em linhas gerais, a análise do volume de controle dará ao engenheiro uma ideia das cargas dominantes em um sistema. Isso lhe dará uma sensação inicial sobre qual caminho seguir ao projetar dispositivos ou estruturas, e deve ser o passo inicial a ser dados antes de buscar qualquer projeto ou análise detalhado através da formulação diferencial.

O princípio principal por trás da formulação do volume de controle é substituir os detalhes de um sistema exposto a um fluxo de fluido por um diagrama corpo livre simplificado definido por uma superfície fechada imaginária apelidada de volume de controle. Este diagrama deve conter todas as forças da superfície e do corpo, o fluxo líquido de impulso linear através dos limites do volume de controle, e a taxa de mudança de impulso linear dentro do volume de controle. Essa abordagem implica definir inteligentemente o volume de controle de maneiras que simplificam a análise ao mesmo tempo que capturam os efeitos dominantes no sistema. Esta técnica será demonstrada com um jato de avião em uma placa plana em diferentes ângulos. Usaremos a análise de volume de controle para estimar a carga aerodinâmica na placa, e compararemos nossos resultados com as medidas reais da força resultante obtida com um equilíbrio aerodinâmico.

Um volume de controle (CV) é definido por uma superfície fechada imaginária, apelidada de superfície de controle (CS), definida arbitrariamente para estudar o efeito do fluxo em torno de objetos e sistemas. A Figura 1 mostra um exemplo de um volume de controle contendo uma região de fluxo que gira em torno de um objeto sólido. O fluxo nas proximidades do objeto é altamente complexo, e gostaríamos de evitar essa complexidade para estimar o efeito global do fluxo sobre o elemento de suporte. Uma vez definido, o CV torna-se um diagrama corporal livre que captura as interações entre o fluxo e o objeto fechado que dão origem a cargas no sistema de suporte. Para isso, igualamos as forças da superfície e do corpo no CV com a mudança do momento linear do fluxo que passa pelo CV. As forças da superfície são pressão, cisalhamento induzido pelo fluxo, e quaisquer reações dos sólidos "cortados" pelo volume de controle. As forças do corpo são basicamente o peso de tudo contido no volume de controle, incluindo sólidos e fluidos, e qualquer outra força induzida por efeitos volumosos, como campos eletromagnéticos. A mudança no momento linear do fluxo é o efeito adicional do fluxo líquido de impulso através do CS e a taxa de mudança de impulso contida no CV. Todos esses efeitos podem ser resumidos na equação para conservação do momento linear na forma integral:

(1)

Aqui, estão as forças da superfície e são as forças do corpo. O primeiro termo no lado direito da equação (1) representa a taxa de mudança de dinâmica dentro do volume de controle, enquanto o segundo termo representa o fluxo líquido de impulso através da superfície de controle. A diferença vetorial é a velocidade relativa entre o CV e o fluxo, e o vetor é a unidade externa normal para o diferencial da área. O produto ponto entre a velocidade relativa e representa o componente de velocidade que cruza o CS, e a partir de agora contribui para a troca de impulso linear. O sinal deste produto ponto é negativo onde o fluxo de impulso é direcionado para o CV e positivo onde ele é direcionado para longe do CV. Nesta forma, a equação (1) é o equilíbrio do momento linear em relação a um quadro inercial de referência. Note que (1) é uma equação vetorial, o que significa que em geral tem três componentes independentes. Com isso em mente, o analista precisa ter cuidado ao estabelecer o conjunto de forças que equilibram mudanças no momento linear para cada coordenada.

Para a presente demonstração, temos a configuração mostrada na Figura 1, onde um CV fixo inclui uma placa que é exposta a um jato de avião. Como o fluxo de jato é constante, não há mudança de dinâmica dentro do CV, então o primeiro termo no lado direito da equação (1) desaparece. Além disso, o CV não se move, então . Assim, a soma das forças no CV equilibra-se com o fluxo líquido de impulso através do CS.

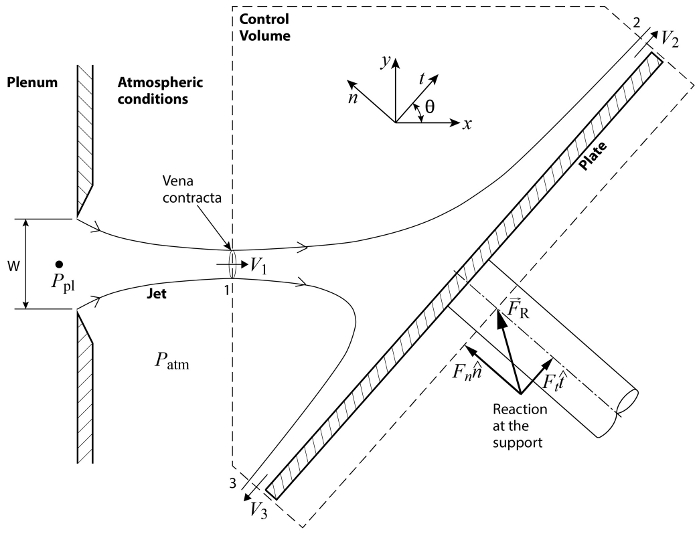
Figura 1. Esquema de configuração básica. Um jato de avião sai do plenário através de uma fenda de largura W. O jato se põe em uma placa inclinada e é desviado enquanto exerce uma carga na superfície.

Considerando a configuração na Figura 1, o impulso flui para o CV através da porta 1 e deixa o CV através das portas 2 e 3. O CV cruza o jato de entrada na vena contracta, (para mais informações, veja o vídeo "A Interação de Pressão e Velocidade: jato impinging em uma placa inclinada") que é o primeiro lugar em que as aerodinâmicas se tornam paralelas e, como resultado, a pressão estática através do jato torna-se homogênea e corresponde ao valor da pressão circundante, ou seja, pressão atmosférica. Da mesma forma, os portos 2 e 3 estão localizados longe o suficiente da região de impacto para permitir que as aerodinâmicas se tornem paralelas e a pressão para coincidir com a do entorno. Como resultado, a pressão em todos os lugares sobre o CS é igual à pressão atmosférica, . Em consequência, dado que a pressão é distribuída de forma homogênea ao redor do CS, sua força líquida no volume de controle é zero. Além disso, uma vez que o CS foi desenhado perpendicular para os fluxos de entrada e saída, não há qualquer carga de cisalhamento induzida pelo fluxo no CS. Em resumo, a equação (1) simplifica para a seguinte relação para o caso ilustrado na Figura 1

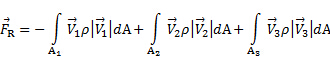(2)

Aqui, é a reação do sistema de suporte resultante da transmissão do carregamento aerodinâmico que o jato exerce sobre a placa. Como mostrado na Figura 1, esta reação está localizada na parte do volume de controle que "corta" através do sistema de suporte da placa. Isso é considerado uma força superficial no sentido de que este corte imaginário seria parte da superfície de controle. Como é a única interação com o volume de controle não associado ao fluxo de impulso, é o único termo no lado esquerdo das equações (1) e (2). Observe comparando essas equações entre si que os produtos de ponto dentro das integrais resultam simplesmente nas magnitudes dos vetores de velocidade correspondentes porque estão alinhados com os vetores da área. Além disso, como dito anteriormente, seu sinal diz se o fluxo de impulso é direcionado para o CV (-) ou longe dele (+). Se assumirmos ainda que a velocidade nos portos é aproximadamente homogênea, e que o fluxo é incompressível, as velocidades e densidades podem ser tomadas fora das integrações e equação (2) torna-se:

(3)

Rigorosamente falando, o perfil de velocidade nunca é perfeitamente homogêneo, e essa simplificação requer uma multiplicação por um coeficiente de correção, cujo valor depende dos detalhes do perfil de velocidade. Em uma determinada porta de fluxo, este coeficiente é definido como a razão entre o fluxo de impulso exato e o fluxo de impulso estimado a partir da velocidade média:

(4)

Em fluxos turbulentos este coeficiente é muito próximo de 1 porque o perfil de velocidade tende a ser próximo de homogêneo. Uma vez que este é o caso do presente experimento, a equação (3) é uma aproximação razoável para as medidas atuais. Mas se a taxa de fluxo fosse reduzida ou a posição da placa se movesse mais para baixo até atingir as condições de fluxo laminar, seria necessário resolver as integrais do lado direito da equação (2) sem aproximação. Com base na Figura 1, pode ser decomposto em suas coordenadas normais e tangentes para a placa . Onde 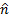e são os vetores da unidade em cada coordenada e 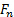são as magnitudes das projeções de cada coordenada. Assim, a equação (3) pode ser decomposta como:

(5)

Observe que o sinal de menos no componente normal desaparece porque a projeção do eixo normal é negativa. Queremos determinar a carga normal na placa com este estudo, pois ela tende a ser o componente mais relevante do ponto de vista estrutural. A partir da equação (4), obtemos a carga normal na placa:

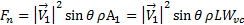(6)

Aqui, é o vão da placa e é a largura do jato na vena contracta. Em geral, a relação de contração entre a largura de saída do jato, e a vena contracta é muito próxima de [2, 3, 4]:

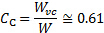(7)

Em resumo, a força normal na placa pode ser estimada a partir da seguinte relação:

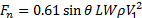(8)

Aqui, definimos para a simplicidade. Por outro lado, o valor do termo é determinado usando a equação de Bernoulli entre o plenário e o vena contracta (ver Figura 2 para referência). A velocidade dentro do plenário é considerada insignificante, e dado que o jato é horizontal, mudanças de altura entre o plenário e a vena contracta desaparecem. Assim, a equação de Bernoulli torna-se:

(9)

Lembre-se que a pressão na vena contracta corresponde à pressão circundante, que é atmosférica. Assim, a pressão dinâmica na vena contracta segue:

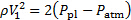(10)

A equação substitutivo (9) na equação (7) dá o resultado final para estimar a força normal na placa com base nas características do jato de avião:

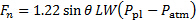(11)

Este resultado vem da análise de volume de controle da conservação do momento linear. Para ter uma avaliação de sua precisão, vamos comparar essas estimativas com medições diretas da força. Para este fim, os componentes horizontais ( 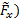e verticais ( da força total representada na Figura 2 são capturados por um equilíbrio aerodinâmico. Para determinar os componentes desta força medida no sistema de coordenadas, utilizamos a seguinte transformação coordenada:

(12)

(13)

Quando um tilde foi adicionado para enfatizar que essas forças são obtidas por medição direta com um equilíbrio aerodinâmico.

1. Definindo a instalação

1. Certifique-se de que não há fluxo na instalação.
2. Conecte a porta positiva do transdutor de pressão à torneira de pressão do plenário ( ).
3. Deixe a porta negativa do transdutor de pressão aberta à atmosfera ( ).
4. Registo do transdutor de Volts para Pascals ( ).
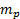5. Regisso da largura de saída do jato.
6. Registo o vão da placa.
7. Registo as constantes de conversão do equilíbrio de força de Volts para Newton (força horizontal: ; força vertical: ).
8. Configurar o sistema de aquisição de dados para amostrar a uma taxa de 100 Hz para um total de 1000 amostras (ou seja, 10s de dados).
9. Monte a placa de impacto no equilíbrio da força e ajuste suas saídas para zero.

2. Registro dos dados

1. Coloque o ângulo da placa em 90^o (ver Figura 2 para referência).
2. Ligue a instalação de fluxo.
3. Registo da leitura do transdutor de pressão em Volts, que corresponde à diferença de pressão entre o Plenário e a atmosfera ( ).
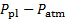4. Regissão os dados de força usando o sistema de aquisição de dados.
5. Multiplique os valores adquiridos (em Volts) pelos fatores de conversão de força ( e ) e digite os resultados na tabela 1.
6. Desligue a instalação de fluxo.
7. Mude o ângulo da placa.
8. Repetir as etapas 2.2 a 2.6 para os seguintes ângulos:

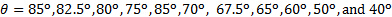
Figura 2 . Configuração experimental. (A): Detalhe do sistema de admissão para pressurizar o plenário sob pressão . (B): lado de descarga com placa de impacto. (C): Detalhe da fenda de descarga. Clique aqui para ver uma versão maior desta figura.

3. Análise de dados

1. Calcule a força normal medida pelo equilíbrio usando a equação(11) e grave-a na tabela 1.
2. Determine o valor teórico da força normal da equação (10) e registe-a na tabela 1.
3. Calcule a discordância entre os dois valores como um por cento.

Tabela 1 . Parâmetros básicos para estudo experimental.

Parâmetro	Valor
Largura do bocal do jato(W)	19,05 mm
Extensão da placa(L)	110,49 cm
Constante de calibração do transdutor (m_p)	141.3829 Pa/V
Equilibre o coeficiente horizontal (m_x)	22.2411 N/V
Coeficiente vertical de equilíbrio (m_y)	4.4482 N/V

A Figura 3 mostra uma comparação entre a carga normal na placa plana medida diretamente de um equilíbrio aerodinâmico e estimada a partir da conservação do momento linear. Em geral, a análise do momento linear capturou a tendência dominante das medições diretas à medida que o ângulo de impacto muda. As discrepâncias nessas medidas variaram não monotonicamente com o ângulo de impacto. Para ângulos de impacto na faixa 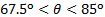, e para , as discrepâncias estão abaixo de 6%. São maiores para os outros ângulos, mas nunca superiores a 12,5%. Parece haver um cruzamento ao 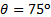redor, no qual a tendência de discrepâncias inverte: as medidas apresentam cargas normais mais altas do que a análise de impulso linear para 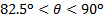. Essas diferenças nas tendências podem ser devidas ao fato de que a análise do momento linear assume mudanças inviscid, não dissipadoras, no momento linear, enquanto as medições diretas não podem evitar o efeito da viscosidade no fluxo. Para o intervalo, o componente da tesoura torna-se dominante e, portanto, efeitos turbulentos da camada de fronteira podem ser importantes. Neste caso, flutuações de velocidade normais da parede devido à turbulência podem ser responsáveis pelo aumento da carga normal. Por outro lado, a velocidade axial do jato experimenta uma redução significativa no alcance 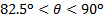enquanto ele se transforma em se tornar dominantemente tangente à parede. Esse efeito provavelmente permitirá que a viscosidade se dissipe a viscosidade devido a uma redução nos valores locais do número de Reynolds, e isso resultaria em valores reduzidos da carga normal.

Tabela 2. Resultados representativos.

θ	F י_x(N)	F י_y (N)	F י_n (N)	F_n (N)	ε
90o	15.257	9.034	15.257	16.773	9.9
85o	15.151	9.831	15.950	16.709	4.8
82,5o	15.035	10.231	16.242	16.630	2.4
80o	15.929	10.498	17.510	16.518	5.7
75o	14.248	10.453	16.468	16.202	1.6
70o	13.518	11.405	16.604	15.762	5.1
67,5o	13.100	11.294	16.425	15.496	5.7
65o	12.771	11.579	16.468	15.202	7.7
60o	11.881	11.863	16.221	14.526	10.5
50o	9.746	11.241	14.691	12.849	12.5
40o	6.357	9.444	11.320	10.782	4.8

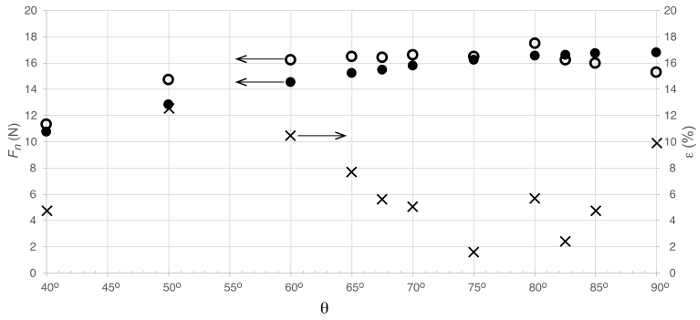
Figura 3. Resultados representativos. Carregue na placa como resultado de um jato em impacto. Os símbolos representam: : medição direta de carga; : estimativa da conservação do momento linear; : erro percentual entre medições experimentais e estimativa teórica. 

Demonstramos a aplicação da análise de volume de controle da conservação do impulso linear para determinar as forças exercidas por um jato que se ingi em uma placa plana. Esta análise mostrou-se simples de aplicar, e deu uma estimativa em massa satisfatória de cargas sem exigir conhecimento detalhado do padrão de fluxo ao redor da placa. Embora houvesse algumas discrepâncias (tanto em magnitude quanto em tendência) devido à suposição básica de transformação inviscida do momento, essa técnica oferece um meio de obter uma rápida estimativa do comportamento do sistema sem se aprofundar em um estudo detalhado do fluxo de fluidos. Portanto, esta é uma ferramenta poderosa para o analista de engenharia prever, por exemplo, a viabilidade de desenvolver um determinado sistema de engenharia com um investimento mínimo de tempo e recursos. Uma vez que esta primeira análise é realizada para determinar a viabilidade, o engenheiro pode passar para uma análise de fluxo mais detalhada usando, por exemplo, a dinâmica do fluido computacional.

Controlar a análise de volume de conservação do momento linear é uma poderosa ferramenta para a engenharia de fluidos. Encontra aplicação em uma ampla variedade de problemas para contornar métodos mais envolvidos, como análise diferencial. Alguns exemplos desta análise podem ser descritos:

Design da lâmina da turbina Pelton: em geral, uma lâmina de turbina Pelton deve ser projetada para converter a maior quantidade de impulso linear em torque. Isso é conseguido determinando a geometria da lâmina que maximiza a mudança no momento linear dos jatos d'água. Para isso, o resultado típico da análise do volume de controle é que o jato deve ser feito para virar em si mesmo, ou seja, 180^o. Este é, em geral, um desafio técnico para um dispositivo rotativo, mas dá ao analista uma orientação inicial para uma análise mais detalhada usando outras ferramentas.

Arrastar carga em estruturas civis: um dos desafios da engenharia civil é projetar estruturas que resistam à carga de vento. A fim de prever os efeitos do vento em uma estrutura em tamanho real, é possível realizar experimentos com um modelo em baixa escala em túneis de vento ou água. Para isso, é possível utilizar a análise de volume de controle da conservação do momento linear com base em medições de velocidade rio acima e rio abaixo do modelo para determinar a carga efetiva no protótipo. Esse método simplifica a campanha experimental e economiza tempo, esforço e dinheiro na preparação para a construção de uma estrutura em escala real.