Determinación de las fuerzas de impacto en una placa plana con el método del control del volumen
Visión general
Fuente: Ricardo Mejía-Alvarez y Hussam Hikmat Jabbar, Departamento de ingeniería mecánica, Universidad Estatal de Michigan, East Lansing, MI
El propósito de este experimento es demostrar las fuerzas en cuerpos como el resultado de cambios en el ímpetu linear del flujo alrededor de ellos usando una formulación del volumen de control [1, 2]. El análisis del volumen de control se centra en el efecto macroscópico de flujo en sistemas de ingeniería, en lugar de la descripción detallada que puede lograrse con un análisis diferencial. Cada una de estas dos técnicas tienen un lugar en la caja de herramientas de un analista de ingeniería, y deben considerarse complementarios en lugar de enfoques concurrentes. En términos generales, análisis del volumen control dará al ingeniero una idea de las cargas dominantes en un sistema. Esto le dará a él/ella una sensación inicial sobre qué ruta para dedicarse al diseño de dispositivos o estructuras y deberían idealmente ser el paso inicial antes de perseguir cualquier diseño detallado o análisis a través de la formulación diferencial.
El principio principal detrás de la formulación del volumen de control es cambiar los detalles de un sistema expuesto a un fluido por un diagrama de cuerpo libre simplificada definido por un imaginario cerrado superficie como del volumen de control. Este diagrama debe contener todas las fuerzas superficie y el cuerpo, el flujo neto de ímpetu linear a través de las fronteras del volumen de control y la tasa de cambio del ímpetu linear dentro del volumen de control. Este enfoque implica definir inteligentemente el volumen de control de manera que simplifican el análisis al mismo tiempo que captura los efectos dominantes en el sistema. Esta técnica se demostrará con un chorro de plano que inciden sobre una placa plana en diferentes ángulos. Utilizará el análisis del volumen control para estimar la carga aerodinámica en la placa y va a comparar nuestros resultados con las medidas reales de la fuerza resultante obtenida con un equilibrio aerodinámico.
Principios
Un volumen de control (CV) es definido por una superficie cerrada imaginaria, como la superficie de control (CS), definida arbitrariamente para estudiar el efecto del flujo alrededor de objetos y sistemas. La figura 1 muestra un ejemplo de un volumen de control que contiene una región de flujo alrededor de un objeto sólido. El flujo en la vecindad inmediata del objeto es muy complejo, y nos gustaría evitar esa complejidad con el fin de estimar el efecto global del flujo en el elemento de apoyo. Una vez definido, el CV se convierte en un diagrama de cuerpo libre que captura las interacciones entre el flujo y el objeto cerrado que dan lugar a cargas en el sistema de apoyo. Para ello, igualamos la superficie y las fuerzas del cuerpo en el CV con el cambio de ímpetu linear del flujo que pasa a través de la CV. Las fuerzas de superficie son presión, esfuerzo cortante inducido por el flujo y cualquier reacción de los sólidos "cortados" por el volumen de control. Las fuerzas de cuerpo son básicamente el peso de todo el contenido en el volumen de control, incluyendo sólidos, líquidos y cualquier otra fuerza inducida por efectos volumétricos tales como campos electromagnéticos. El cambio en ímpetu linear del flujo es el efecto añadido del flujo neto de ímpetu a través de la CS y la tasa de cambio del ímpetu en el CV. Todos estos efectos se pueden resumir en la ecuación para la conservación del ímpetu linear en forma integral:
 (1)
(1)
Aquí,  son las fuerzas de superficie y
son las fuerzas de superficie y  son las fuerzas de cuerpo. El primer término del lado derecho de la ecuación (1) representa la tasa de cambio del ímpetu interior del volumen de control, mientras que el segundo término representa el flujo neto de ímpetu a través de la superficie de control. La diferencia del vector
son las fuerzas de cuerpo. El primer término del lado derecho de la ecuación (1) representa la tasa de cambio del ímpetu interior del volumen de control, mientras que el segundo término representa el flujo neto de ímpetu a través de la superficie de control. La diferencia del vector  es la velocidad relativa entre el CV y el flujo y el vector de
es la velocidad relativa entre el CV y el flujo y el vector de  es la unidad hacia fuera normal que el diferencial de área. El producto escalar entre la velocidad relativa y
es la unidad hacia fuera normal que el diferencial de área. El producto escalar entre la velocidad relativa y  representa el componente de velocidad que cruza el CS y en lo sucesivo contribuye al intercambio de ímpetu linear. La muestra de este producto de punto es negativa donde se dirige el flujo de momentum en el CV y positivo donde se dirige lejos de la CV. De esta forma, la ecuación (1) es el balance de momentum lineal en relación a un marco inercial de referencia. Tenga en cuenta que (1) es una ecuación vectorial, que significa que en general consta de tres componentes independientes. Con esto en mente, el analista debe tener cuidado en establecer el conjunto de fuerzas que equilibrio cambios en ímpetu linear para cada coordenada.
representa el componente de velocidad que cruza el CS y en lo sucesivo contribuye al intercambio de ímpetu linear. La muestra de este producto de punto es negativa donde se dirige el flujo de momentum en el CV y positivo donde se dirige lejos de la CV. De esta forma, la ecuación (1) es el balance de momentum lineal en relación a un marco inercial de referencia. Tenga en cuenta que (1) es una ecuación vectorial, que significa que en general consta de tres componentes independientes. Con esto en mente, el analista debe tener cuidado en establecer el conjunto de fuerzas que equilibrio cambios en ímpetu linear para cada coordenada.
Para la presente manifestación, contamos con la configuración que se muestra en la figura 1, donde un currículum fijo incluye una placa que se expone a un chorro plano. Puesto que el flujo de chorro es constante, no hay ningún cambio del ímpetu en el CV, por lo que el primer término del lado derecho de la ecuación (1) desaparece. Además, el CV no se mueve, lo  . Por lo tanto, la sumatoria de fuerzas en el CV se equilibra con el flujo neto de ímpetu a través de la CS.
. Por lo tanto, la sumatoria de fuerzas en el CV se equilibra con el flujo neto de ímpetu a través de la CS.
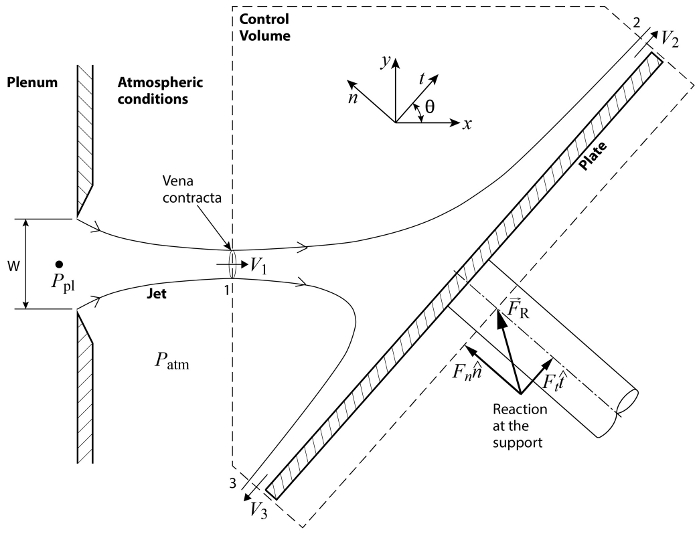
Figura 1 . Esquema de configuración básica. Un jet de avión sale el pleno a través de una rendija de anchura W. El chorro incide sobre una placa inclinada y es desviado y ejerciendo una carga en la superficie.
Teniendo en cuenta la configuración en la figura 1, impulso fluye en el CV a través del puerto 1 y deja el CV a través de los puertos 2 y 3. El CV cruza el chorro de entrada en la vena contracta, (para más información, por favor ver el video "la interrelación entre presión y velocidad: jet que inciden sobre una placa inclinada") que es el primer lugar en que las líneas se convierten en paralelo y, en consecuencia, la presión estática a través del chorro se vuelve homogénea y coincide con el valor de la presión circundante, es decir, la presión atmosférica  . Del mismo modo, los puertos 2 y 3 se encuentran lo suficientemente lejos de la región afectar para permitir que la optimiza para convertirse en paralelo y la presión para que coincida con la de los alrededores. Como resultado, la presión por todas partes en el CS es igual a la presión atmosférica,
. Del mismo modo, los puertos 2 y 3 se encuentran lo suficientemente lejos de la región afectar para permitir que la optimiza para convertirse en paralelo y la presión para que coincida con la de los alrededores. Como resultado, la presión por todas partes en el CS es igual a la presión atmosférica,  . En consecuencia, dado que la presión se distribuye homogéneamente en el CS, la fuerza neta en el volumen de control es cero. Además, puesto que el CS era dibujada perpendicular a los flujos de entrada y salida, no hay ninguna carga del esquileo inducido por el flujo en el CS. En Resumen, la ecuación (1) se simplifica a la siguiente relación para el caso ilustrado en la figura 1
. En consecuencia, dado que la presión se distribuye homogéneamente en el CS, la fuerza neta en el volumen de control es cero. Además, puesto que el CS era dibujada perpendicular a los flujos de entrada y salida, no hay ninguna carga del esquileo inducido por el flujo en el CS. En Resumen, la ecuación (1) se simplifica a la siguiente relación para el caso ilustrado en la figura 1
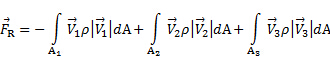 (2)
(2)
Aquí,  es la reacción del sistema de apoyo que resulta de la transmisión de la carga aerodinámica que ejerce el chorro sobre la placa. Como se muestra en la figura 1, esta reacción se encuentra en la porción del volumen de control que "atraviesa" el sistema de apoyo de la placa. Esto se considera una fuerza de superficie en el sentido que este imaginario sería parte de la superficie de control. Puesto que
es la reacción del sistema de apoyo que resulta de la transmisión de la carga aerodinámica que ejerce el chorro sobre la placa. Como se muestra en la figura 1, esta reacción se encuentra en la porción del volumen de control que "atraviesa" el sistema de apoyo de la placa. Esto se considera una fuerza de superficie en el sentido que este imaginario sería parte de la superficie de control. Puesto que  es la única interacción con el volumen de control no asociado con el flujo de momentum, es el único término en el lado izquierdo de las ecuaciones (1) y (2). Tenga en cuenta al comparar estas ecuaciones con los demás que los productos dentro de las integrales en las magnitudes de los vectores velocidad correspondientes porque se alinean con los vectores de la zona. También, como dije antes, su signo indica si el flujo de impulso se dirige en el CV (-) o fuera de él (+). Si además suponemos que la velocidad en los puertos es aproximadamente homogénea, y que el flujo es incompresible, la densidad y la velocidad pueden tomarse fuera de las integrales y se convierte en ecuación (2):
es la única interacción con el volumen de control no asociado con el flujo de momentum, es el único término en el lado izquierdo de las ecuaciones (1) y (2). Tenga en cuenta al comparar estas ecuaciones con los demás que los productos dentro de las integrales en las magnitudes de los vectores velocidad correspondientes porque se alinean con los vectores de la zona. También, como dije antes, su signo indica si el flujo de impulso se dirige en el CV (-) o fuera de él (+). Si además suponemos que la velocidad en los puertos es aproximadamente homogénea, y que el flujo es incompresible, la densidad y la velocidad pueden tomarse fuera de las integrales y se convierte en ecuación (2):
 (3)
(3)
Rigurosamente hablando, el perfil de velocidad no es perfectamente homogéneo, y esta simplificación requiere una multiplicación por un coeficiente de corrección,  , cuyo valor depende de los detalles del perfil de velocidad. En un puerto determinado flujo, este coeficiente se define como el cociente entre el flujo de impulso exacto y el flujo de impulso de la velocidad media:
, cuyo valor depende de los detalles del perfil de velocidad. En un puerto determinado flujo, este coeficiente se define como el cociente entre el flujo de impulso exacto y el flujo de impulso de la velocidad media:
 (4)
(4)
En flujos turbulentos este coeficiente es muy cercano a 1 porque el perfil de velocidad tiende a ser cerca de homogéneo. Ya que este es el caso para el presente experimento, la ecuación (3) es una aproximación razonable para las mediciones actuales. Pero si la tasa de flujo reducida o la posición de la placa se movió más lejos río abajo hasta llegar a condiciones de flujo laminar, sería necesario resolver las integrales del lado derecho de la ecuación (2) sin aproximación. Basado en la figura 1,  se puede descomponer en sus coordenadas normales y tangentes a la placa de
se puede descomponer en sus coordenadas normales y tangentes a la placa de  . Donde
. Donde 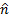 y
y  son los vectores de la unidad en cada coordenada y
son los vectores de la unidad en cada coordenada y 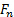 y
y 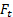 son las magnitudes de las proyecciones de
son las magnitudes de las proyecciones de  en cada coordenada. Por lo tanto, la ecuación (3) se puede descomponer como:
en cada coordenada. Por lo tanto, la ecuación (3) se puede descomponer como:
 (5)
(5)
Nota que el signo menos en el componente normal desaparece porque la proyección de  en el eje normal es negativo. Queremos determinar la carga normal de la placa con este estudio porque tiende a ser el componente más relevante desde el punto de vista estructural. De la ecuación (4), obtenemos la carga normal de la placa:
en el eje normal es negativo. Queremos determinar la carga normal de la placa con este estudio porque tiende a ser el componente más relevante desde el punto de vista estructural. De la ecuación (4), obtenemos la carga normal de la placa:
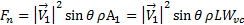 (6)
(6)
Aquí, 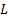 es la placa y
es la placa y 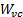 es el ancho del jet en la vena contracta. En general, la relación de contracción entre el chorro de salida ancho,
es el ancho del jet en la vena contracta. En general, la relación de contracción entre el chorro de salida ancho,  , y la vena contracta es muy cerca de [2, 3, 4]:
, y la vena contracta es muy cerca de [2, 3, 4]:
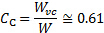 (7)
(7)
En Resumen, la fuerza normal en la placa puede estimarse de la siguiente relación:
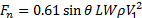 (8)
(8)
Aquí, definimos  para la simplicidad. Por otra parte, el valor del término
para la simplicidad. Por otra parte, el valor del término  se determina usando la ecuación de Bernoulli entre el pleno y la vena contracta (ver figura 2 para la referencia). La velocidad dentro de la cámara se considera insignificante, y dado que el jet es horizontal, cambios de altura entre el pleno y la vena contracta se desvanecen. Por lo tanto, se convierte la ecuación de Bernoulli:
se determina usando la ecuación de Bernoulli entre el pleno y la vena contracta (ver figura 2 para la referencia). La velocidad dentro de la cámara se considera insignificante, y dado que el jet es horizontal, cambios de altura entre el pleno y la vena contracta se desvanecen. Por lo tanto, se convierte la ecuación de Bernoulli:
 (9)
(9)
Hay que recordar que la presión en la vena contracta coincide con la presión circundante, que es atmosférica. Por lo tanto, sigue la presión dinámica en la vena contracta :
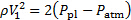 (10)
(10)
Sustituyendo la ecuación (9) en la ecuación (7) da el resultado final para calcular la fuerza normal en la placa según las características del chorro plano:
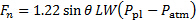 (11)
(11)
Este resultado proviene de lo análisis del volumen control de conservación del ímpetu linear. Para tener una evaluación de su precisión, vamos a comparar estas estimaciones para las mediciones de la fuerza. Con este fin, la horizontal (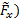 y vertical (
y vertical ( componentes de la fuerza total que se muestra en la figura 2 son capturados por un equilibrio aerodinámico. Determinar los componentes de esta medida fuerza en la
componentes de la fuerza total que se muestra en la figura 2 son capturados por un equilibrio aerodinámico. Determinar los componentes de esta medida fuerza en la  sistema de coordenadas, se utiliza la siguiente transformación de coordenadas:
sistema de coordenadas, se utiliza la siguiente transformación de coordenadas:
 (12)
(12)
 (13)
(13)
Donde un tilde se agregó para enfatizar que estas fuerzas se obtienen por medición directa con un equilibrio aerodinámico.
Procedimiento
1. configuración de la instalación
- Asegúrese de que no hay ningún flujo en la instalación.
- Conecte el puerto positivo del transductor de presión para la toma de presión plenum (
 ).
). - Deje el puerto negativo del transductor de presión abierta a la atmósfera (
 ).
). - Registrar el factor de conversión del transductor de voltios a pascales (
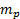 ).
). - Expediente de la anchura de salida del chorro.
- Registrar la duración de la placa.
- Registrar constantes de conversión de equilibrio de la fuerza de voltios a Newton (fuerza horizontal:
 ; vertical de la fuerza:
; vertical de la fuerza:  ).
). - Configurar el sistema de adquisición de datos a la muestra a una frecuencia de 100 Hz para un total de 1000 muestras (es decir, 10s datos).
- Montar la placa de impacto en el equilibrio de fuerza y ajuste sus salidas a cero.
2. grabación de los datos
- Ajuste el ángulo de la placa a 90o (ver figura 2 para la referencia).
- Encienda la facilidad de flujo.
- Registrar la lectura del transductor de presión en voltios, que corresponde a la diferencia de presión entre la cámara y la atmósfera (
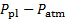 ).
). - Registrar los datos de fuerza usando el sistema de adquisición de datos.
- Multiplicar los valores adquiridos (en voltios) por los factores de conversión de fuerza (
 y
y  ) y escriba los resultados en la tabla 1.
) y escriba los resultados en la tabla 1. - Apague la facilidad de flujo.
- Cambiar el ángulo de la placa.
- Repita los pasos 2.2 a 2.6 para los siguientes ángulos:
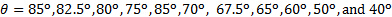

Figura 2. Ajuste experimental. (A): detalle del sistema de admisión para presurizar la cámara a presión  . (B): descarga lateral con placa de choque. (C): detalle de la abertura de descarga. Haga clic aquí para ver una versión más grande de esta figura.
. (B): descarga lateral con placa de choque. (C): detalle de la abertura de descarga. Haga clic aquí para ver una versión más grande de esta figura.
3. Análisis de los datos
- Calcular la fuerza normal medida por el saldo con equation(11) y regístrelo en la tabla 1.
- Determinar el valor teórico de la fuerza normal de la ecuación (10) y registrar en la tabla 1.
- Calcular el desacuerdo entre los dos valores como un porcentaje.
Tabla 1. Parámetros básicos para el estudio experimental.
| Parámetro | Valor |
| Ancho de boquilla de chorro (W) | 19.05 mm |
| Palmo de la placa (L) | 110,49 cm |
| Constante de calibración del transductor (m_p) | 141.3829 Pa/V |
| Coeficiente de equilibrio horizontal (m_x) | 22.2411 N/V |
| Coeficiente de equilibrio vertical (m_y) | 4.4482 N/V |
Resultados
La figura 3 muestra una comparación entre la carga normal sobre la placa plana como medidos directamente con un equilibrio aerodinámico y estimados de conservación del ímpetu linear. En general, el análisis del ímpetu linear capturó la tendencia dominante de medidas directas como los cambios de ángulo de choque. Las discrepancias en las mediciones no monótonamente varían con el ángulo de choque. Para ángulos de choque en la gama de 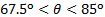 y
y  , las discrepancias son inferiores al 6%. Son mayores para los otros ángulos, pero nunca superior al 12,5%. Parece ser un cruce alrededor de
, las discrepancias son inferiores al 6%. Son mayores para los otros ángulos, pero nunca superior al 12,5%. Parece ser un cruce alrededor de 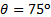 , en que invertir la tendencia de las discrepancias: mediciones presentan mayores cargas normales que análisis del ímpetu linear para
, en que invertir la tendencia de las discrepancias: mediciones presentan mayores cargas normales que análisis del ímpetu linear para  y menor
y menor 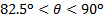 . Estas diferencias en las tendencias podrían ser debido a que el análisis del ímpetu linear supone no viscoso, no disipativos, cambios en ímpetu linear, mientras que mediciones directas no pueden evitar el efecto de la viscosidad sobre el flujo. Para la gama de
. Estas diferencias en las tendencias podrían ser debido a que el análisis del ímpetu linear supone no viscoso, no disipativos, cambios en ímpetu linear, mientras que mediciones directas no pueden evitar el efecto de la viscosidad sobre el flujo. Para la gama de  , el componente de cizallamiento se convierte en dominante y, por tanto, efectos de capa límite turbulento podrían ser importantes. En este caso, las fluctuaciones de la velocidad normal de la pared debido a la turbulencia podrían ser responsables del aumento de la carga normal. Por otro lado, la velocidad axial del chorro experimenta una reducción significativa en la gama
, el componente de cizallamiento se convierte en dominante y, por tanto, efectos de capa límite turbulento podrían ser importantes. En este caso, las fluctuaciones de la velocidad normal de la pared debido a la turbulencia podrían ser responsables del aumento de la carga normal. Por otro lado, la velocidad axial del chorro experimenta una reducción significativa en la gama 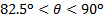 mientras que vuelve a convertirse en dominante tangente a la pared. Es probable que deje viscosidad viscosidad debido a una reducción en los valores locales del número de Reynolds de disipar este efecto, y eso daría lugar a valores reducidos de carga normal.
mientras que vuelve a convertirse en dominante tangente a la pared. Es probable que deje viscosidad viscosidad debido a una reducción en los valores locales del número de Reynolds de disipar este efecto, y eso daría lugar a valores reducidos de carga normal.
Tabla 2 . Resultados representativos.
| Θ | F ̃_x(N) | ̃_y de F (N) | ̃_n de F (N) | F_n (N) | Ε (%) |
| 90o | 15.257 | 9.034 | 15.257 | 16.773 | 9.9 |
| 85o | 15.151 | 9.831 | 15.950 | 16.709 | 4.8 |
| 82.5o | 15.035 | 10.231 | 16.242 | 16.630 | 2.4 |
| 80o | 15.929 | 10.498 | 17.510 | 16.518 | 5.7 |
| 75o | 14.248 | 10.453 | 16.468 | 16.202 | 1.6 |
| 70o | 13.518 | 11.405 | 16.604 | 15.762 | 5.1 |
| 67,5o | 13.100 | 11.294 | 16.425 | 15.496 | 5.7 |
| 65o | 12.771 | 11.579 | 16.468 | 15.202 | 7.7 |
| 60o | 11.881 | 11.863 | 16.221 | 14.526 | 10.5 |
| 50o | 9.746 | 11.241 | 14.691 | 12.849 | 12.5 |
| 40o | 6.357 | 9.444 | 11.320 | 10.782 | 4.8 |

Figura 3 . Resultados representativos. Carga en la placa como consecuencia afectando jet. Símbolos representan:  : directa medición carga;
: directa medición carga;  : estimación de conservación del ímpetu linear;
: estimación de conservación del ímpetu linear;  : error porcentual entre las medidas experimentales y la estimación teórica. Haga clic aquí para ver una versión más grande de esta figura.
: error porcentual entre las medidas experimentales y la estimación teórica. Haga clic aquí para ver una versión más grande de esta figura.
Aplicación y resumen
Hemos demostrado la aplicación del análisis del volumen control de conservación del ímpetu linear para determinar las fuerzas ejercidas por un jet que inciden sobre una placa plana. Este análisis resultó sencillo de aplicar y dio una estimación satisfactoria a granel de cargas sin necesidad de conocer en detalle el patrón de flujo alrededor de la placa. Aunque hubo algunas discrepancias (tanto en magnitud como en tendencia) debido a la asunción básica de transformación no viscoso de impulso, esta técnica ofrece un medio de obtener una rápida estimación del comportamiento del sistema sin profundizar en un estudio detallado de flujo de fluidos. Por lo tanto, esta es una poderosa herramienta para el analista ingeniería para, por ejemplo, predecir la viabilidad de desarrollar un sistema de ingeniería dado con una inversión mínima de tiempo y recursos. Una vez que este primer análisis se realizaron para determinar la viabilidad, el ingeniero puede mover en un análisis más detallado de flujo utilizando, por ejemplo, dinámica de fluidos computacional.
Análisis del volumen control de conservación del ímpetu linear es una poderosa herramienta para la ingeniería de fluidos. Encuentra aplicación en una amplia variedad de problemas para eludir más métodos como análisis diferencial. Unos pocos ejemplos de este análisis se pueden describir:
Diseño de la lámina de turbina Pelton: en general, una lámina de turbina Pelton será diseñada para convertir la mayor cantidad de ímpetu linear en par. Esto se logra mediante la determinación de la geometría de la hoja que maximiza el cambio en el ímpetu linear de chorros de agua. Con este fin, el resultado típico del análisis del volumen de control es que el jet se hagan para dar vuelta alrededor en sí mismo, es decir, 180o. Esto es en general un desafío técnico para un dispositivo giratorio, pero da al analista una orientación inicial para un análisis más detallado usando otras herramientas.
Arrastre de carga en estructuras civiles: uno de los retos de la ingeniería civil es diseñar estructuras que soporte la carga de viento. Para predecir los efectos del viento sobre una estructura de tamaño real, es posible llevar a cabo experimentos con un modelo de escala reducida en túneles de viento o agua. Para ello, es posible utilizar el análisis del volumen control de conservación del ímpetu linear basada en mediciones de velocidad aguas arriba y aguas abajo del modelo para determinar la carga efectiva sobre el prototipo. Este método simplifica la campaña experimental tanto ahorra tiempo, esfuerzo y dinero en preparación para la construcción de una estructura de escala real.
Referencias
- White, F. M. Fluid Mechanics, 7th ed., McGraw-Hill, 2009.
- Munson, B.R., D.F. Young, T.H. Okiishi. Fundamentals of Fluid Mechanics. 5th ed., Wiley, 2006.
- Buckingham, E. Note on contraction coefficients of jets of gas. Journal of Research,6:765-775, 1931.
- Lienhard V, J.H. and J.H. Lienhard IV. Velocity coefficients for free jets from sharp-edged orifices. ASME Journal of Fluids Engineering, 106:13-17, 1984.
Saltar a...
Vídeos de esta colección:

Now Playing
Determinación de las fuerzas de impacto en una placa plana con el método del control del volumen
Mechanical Engineering
26.0K Vistas

Flotabilidad y arrastre en cuerpos sumergidos
Mechanical Engineering
29.9K Vistas

Estabilidad de los buques flotantes
Mechanical Engineering
22.4K Vistas

Propulsión y empuje
Mechanical Engineering
21.6K Vistas

Redes de tuberías y pérdidas de presión
Mechanical Engineering
58.0K Vistas

Enfriamiento y ebullición
Mechanical Engineering
7.7K Vistas

Saltos hidráulicos
Mechanical Engineering
40.9K Vistas

Análisis del intercambiador de calor
Mechanical Engineering
28.0K Vistas

Introducción a la refrigeración
Mechanical Engineering
24.6K Vistas

Anemometría de hilo caliente
Mechanical Engineering
15.5K Vistas

Medición de flujos turbulentos
Mechanical Engineering
13.5K Vistas

Visualización de flujo más allá de un cuerpo no fuselado
Mechanical Engineering
11.8K Vistas

Jet que inciden sobre una placa inclinada
Mechanical Engineering
10.7K Vistas

Enfoque de conservación de la energía para el análisis de sistemas
Mechanical Engineering
7.4K Vistas

Conservación de masa y mediciones de tasa de flujo
Mechanical Engineering
22.6K Vistas
ACERCA DE JoVE
Copyright © 2025 MyJoVE Corporation. Todos los derechos reservados