Constantes de los materiales

Fuente: Roberto León, Departamento de Ingeniería Civil y ambiental, Virginia Tech, Blacksburg, VA

En contraste con la producción de coches o tostadoras, donde se realizan millones de copias idénticas y pruebas del prototipo extensa son posible, cada estructura de ingeniería civil es único y muy caro para la reproducción (Fig. 1). Por lo tanto, ingenieros civiles deben confiar ampliamente en modelado analítico para diseñar sus estructuras. Estos modelos son abstracciones simplificadas de la realidad y se utilizan para comprobar que no se violan los criterios de rendimiento, particularmente los relacionados con la resistencia y rigidez. Para cumplir con esta tarea, los ingenieros requieren dos componentes: (a) un conjunto de teorías que explicar cómo las estructuras responden a las cargas, es decir, cómo se relacionan las fuerzas y deformaciones y (b) una serie de constantes que diferencian dentro de estas teorías como materiales (acero y hormigón) difieren en su respuesta.

Figura 1: Centro de transporte de centro mundial de Comercio (NYC).

Diseño de ingeniería más hoy en día utiliza principios elástico lineales para calcular las fuerzas y deformaciones en estructuras. En la teoría de la elasticidad, varias constantes materiales son necesarios para describir la relación entre el estrés y la tensión. Estrés se define como la fuerza por unidad de área, mientras que la cepa se define como el cambio de dimensión cuando se somete a una fuerza dividida por la magnitud original de esa dimensión. Los dos más comunes de estas constantes son el módulo de elasticidad (E), que el estrés se relaciona con la tensión y relación de Poisson (ν), que es el cociente del lateral a la tensión longitudinal. Este experimento introduce el equipo típico usado en un laboratorio de materiales de construcción para medir la fuerza (o tensión) y deformación (o tensión) y usarlos para medir E y ν de una barra de aluminio típico.

El modelo más común utilizado para el análisis es elasticidad lineal (Ley de Hooke), que postula que los cambios en la fuerza (F) son directamente proporcionales a los cambios de dimensión (Δ). En su forma más simple en los casos de carga uniaxial, fuerza y deformación están relacionados por una única constante (E), o el módulo de elasticidad:

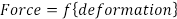(EC. 1)

(EC. 2)

(EC. 3)

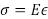(EC. 4)

Como se describe en las ecuaciones anteriores, la tensión y la tensión son ingeniería de cantidades, en comparación con las cantidades verdaderas. Cantidades verdadera requieren uno para medir los cambios en dimensiones locales que ocurren mientras que se aumentan las fuerzas pequeño pero finitos. Experimentalmente, esta hazaña es muy difícil de lograr, incluso con los avances recientes en tecnologías de medición sin contacto. Para estos cálculos, uno puede asumir que los cambios son insignificantes y utilizan el área original (₀) y longitud (L₀).

Para determinar el módulo de elasticidad de las ecuaciones anteriores, hay que tener una manera de determinar los cambios en fuerza y longitud como un espécimen es cargado. En un experimento crudo, uno podría utilizar una báscula de baño y una regla para realizar estas tareas. En primer lugar, uno podría tomar una gruesa banda de caucho, medir sus dimensiones y marcar dos puntos en el grupo separados por una pulgada. Luego, uno podría Coloque un recipiente abierto a escala y añadir agua hasta que la lectura es de diez libras. Entonces uno podría suspender el envase con la goma y medir cuánto se han separado las dos marcas. Esta medida nos dará todos los datos necesarios para el cálculo de E para el caucho ya que contamos con todos los valores necesarios para solucionar para E en Eqs. (2) a (4). Sin embargo, será muy grandes incertidumbres y errores asociados con la medición debido al dispositivo de medición muy crudo. Puesto que la magnitud de tensión necesita ser medido para construcción típica materiales son del orden de 1 x 10^-6, mucho más precisos medidores son necesarios para determinar constantes de material experimental. Para aplicaciones de ingeniería más comunes, estas mediciones se basan en medidores de tensión de resistencia eléctrica. Como estos dispositivos se utilizarán a lo largo de los siguientes videos, se dará a continuación una descripción de sus principios de funcionamiento.

Un medidor de tensión es un alambre largo enrollado incrustado en una matriz de soporte (Fig. 2). Las galgas extensiométricas se pegan al material sometido a prueba con un epoxy de alta resistencia. Cuando el material se deforma, cambian los cables de longitud y su resistencia cambia ligeramente como resultado. Cuando el medidor se inserta como parte de un circuito puente de Wheatstone, estos cambios pueden ser detectados como cambios en el voltaje. El advenimiento de sistemas de medición digital ha reducido considerablemente de ruido de fondo y otras fuentes de error dentro del circuito, mejorando la precisión en el voltaje de que cambios pueden medirse hoy. Las galgas extensiométricas se calibran utilizando una constante conocida como factor gage, por lo que su producción está relacionada linealmente con la tensión para un rango de tensión dado bajo una determinada tensión de entrada.

Un medidor de tensión mide la tensión en solamente una dirección. Para obtener el estado completo de la tensión en un punto sobre una superficie, una roseta protector gage, que se compone de tres medidores de tensión alineadas a 45 º a uno otro es necesario (Fig. 3). Con estas medidas en tres direcciones diferentes, todo el estado de tensión en una superficie se puede definir mediante el uso de principios como el círculo de Mohr para el cálculo de las tensiones y las tensiones principales máximas y mínimas.

Figura 2 : Galgas extensiométricas.

Figura 3 : Galgas extensiométricas roseta.

Las medidas de fuerza también se hacen con galgas de tensión; sin embargo, estas medidas se toman generalmente en una configuración de puente completo (es decir, las resistencias internas en un circuito de puente son sustituidos por medidores de activos externos de Wheatstone) dando por resultado un dispositivo llamado una célula de carga. La célula de carga es generalmente un cilindro grueso, de alta resistencia de acero con dos medidores instalados longitudinalmente y dos instalado transversalmente para eliminar los efectos de la relación de Poisson. La calibración de una célula de carga requiere utilizar pesos muertos para que la tensión de salida del circuito puede estar relacionada con una carga determinada. En los Estados Unidos, el Instituto Nacional de ciencia y tecnología (NIST) calibra células de carga hasta a 5 millones kN mediante mecanismos de palanca y pesos muertos. Todas las células de carga utilizadas en los Estados Unidos deben ser trazables a esta fuente de calibración. En la práctica, trazabilidad es decir A la célula de carga está calibrado por el NIST con pesos muertos, llevados a otros laboratorios e instalado en serie con la carga de la célula B. Por último, célula de carga B se calibra basado en comparar su producción a la salida de la célula de carga A. Todas las células de carga deben calibrarse periódicamente para garantizar que funcionan correctamente.

Normalmente, la célula de carga está instalada en una máquina de ensayos universal (UTM). Una UTM consta de un marco uno mismo-reaccionar con dos columnas de tornillo que se giran por un motor (Fig. 4). Un espécimen de la prueba de sujeción en los puños UTM y girando la columna de tornillo que la cruceta se mueve hacia arriba, las fuerzas de tracción se introducen en la muestra. La fuerza aplicada se mide por la célula de carga, que se instala en serie con la muestra. Por otro lado, si los rodillos están instalados en vez de apretones a la tracción y las columnas de tornillo se mueven hacia abajo, fuerzas de compresión se introduzcan la probeta (es decir, para probar cilindros de hormigón).

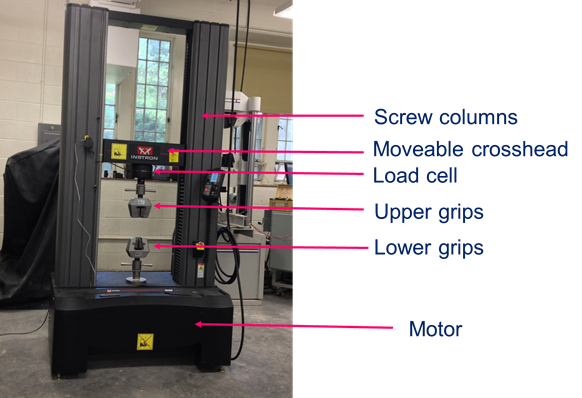
Figura 4 : Máquina de prueba universal.

Ahora que se ha demostrado cómo medir tensión y fuerza, se discutirá un tratamiento más general de la teoría de la elasticidad. Mirando una pieza genérica de una estructura sometida a cargas, se pueden escribir las ecuaciones de equilibrio para fuerzas y momentos a lo largo de los ejes.

Esto se traduce en una serie de ecuaciones para el normal (ε) y tensiones de corte (γ) de la forma:

(EC. 5)

(EC. 6)

Seis ecuaciones de este tipo, tres cepas normales (ε_xy ε_y ε_z) y tres para las cepas del esquileo (γ_xy,_yz γy γ_zx) son necesarios para establecer las deformaciones globales. Estas ecuaciones contienen tres materiales constantes: el módulo de elasticidad (E), relación de Poisson (ν) y el módulo de cizalladura (G). Como se muestra en la ecuación anterior, el módulo del esquileo es el cambio de deformación angular dado un esfuerzo cortante o tracción superficial. Cociente de Poisson se define como:

(EQ. 7)

Puede demostrarse:

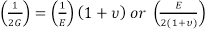= G (EC. 8)

Así, sólo dos de las tres constantes deben determinarse para definir los tres. Hay numerosas otras constantes derivadas que se utilizan en teoría de la elasticidad, que se pueden derivar de estas medidas. Por ejemplo, el módulo a granel (B), o el cambio relativo en el volumen de un cuerpo producido por una tensión de compresión o tracción de unidad actúa uniformemente sobre su superficie, es:

De Eqs. (5) y (6), uno puede determinar el estado de tensiones en una superficie si se realizan al menos tres medidas de tensión independiente. Si se utiliza un medidor de tensión de roseta, que cuenta con tres medidores a 45° a uno otro (Fig. 3) en lugar de un solo calibre longitudinal, entonces uno puede encontrar las tensiones principales máximas y mínimas (ε₁, ε₂) y el ángulo (Φ) entre las cepas medidos y las cepas principales del círculo de Mohr.

De una roseta rectangular galgas extensiométricas, como se muestra en la figura 3 donde los medidores están en 45 grados uno al otro:

(EC. 9)

Φ =

La gama de cepas que sostenga las relaciones elástico lineales es entre cero y el límite proporcional del material. En este experimento, que se utiliza de aluminio, la gama de cepas se mantendrá muy por debajo de ese límite.

Vamos a utilizar una viga cantilever sencilla equipada con medidores de tensión para ayudar a ilustrar los conceptos de tensión principal y las tensiones y el cálculo del módulo de Young (E) y cociente de Poisson (ν).  La viga voladiza se cargará progresivamente con un sistema de pesos y los correspondientes cambios en tensión registrada.  Las tensiones correspondientes pueden calcularse de la ecuación de tensión flexión simple:

(EC. 11)

donde M es el momento (o fuerza multiplicada por su brazo de palanca), c es la distancia desde el baricentro a la fibra extrema en la viga en toda su profundidad (), y es el momento de inercia, de donde b es el ancho de la viga y t es su espesor.

Módulo de elasticidad y de Poisson

Se asume aquí que los estudiantes han sido capacitados en el uso y precauciones de seguridad necesarias para operar la máquina de prueba universal.

1. Obtener un aluminio rectangular de la barra (12 pulg x 1 pulg x 1/4 en.); un aluminio 6061 T6xxx o más fuerte se recomienda. Debe perforarse un orificio de 1 pulgada del extremo de una viga para servir como un punto de carga.
2. Marcar una ubicación en la viga de 8,0 pulgadas desde el centro del agujero en la parte superior de la viga. Dibuja marcas de alineación para los medidores de tensión de roseta y asegúrese de que los ejes de la roseta están inclinados en un ángulo pequeño (aproximadamente 10° a 15°) al eje longitudinal de la viga.
3. Marcar una ubicación similar en la superficie inferior de la viga. Un solo galgas extensiométricas se instalará aquí y deben estar alineada con los ejes longitudinales de la viga.
4. Medir el ancho (b) y espesor (t) de la barra cuidadosamente usando pinzas. Realizar tres repeticiones en tres lugares diferentes para obtener un buen promedio de las dimensiones. De estas mediciones, calcular el momento de inercia (I) y la distancia desde el eje neutro a la fibra extrema de la barra (c = t/2).
5. Obtener un medidor de tensión de roseta con una red de detección de aproximadamente ¼ pulg. de largo por 1/8 mm de ancho en cada calibre y una sola tensión de similar calibre. Tenga en cuenta los factores de calibración (o factor gage) para todos los calibres.
6. Para instalar el medidor de tensión de roseta, primero desengrasar y limpiar la superficie con cuidado. lijar la superficie con papel de lija más fino progresivamente hasta obtener una superficie muy lisa; Limpie la superficie con un neutralizador; y las galgas extensiométricas según las especificaciones del fabricante del pegamento. Deje que el pegamento curar correctamente antes de proceder.
7. Probar la resistencia de los calibradores (típicamente 120 ohmios) y su corriente de fuga a la barra (resistividad, idealmente mayor de 5 Mohms) antes de proceder.
8. Repita los pasos del 1.5 a 1.7 para la gage solo ser instalado en la parte inferior.
9. Introduzca al espécimen en el aparato de voladizo y garantizar adecuadamente.
10. Conectar los medidores de tensión en un dispositivo de grabación, como un indicador de tensión de Vishay P3. Asegúrese que el cableado es correcto según las instrucciones del indicador de tensión y que sabes que canal corresponde a cada galgas extensiométricas.
11. Entre los factores de calibre apropiado para cada calibre en el indicador.
12. Comprobar la calibración del dispositivo introduciendo un voltaje conocido que resultará en una lectura de 5000με en un factor de calibre de 2.00.
13. Carga inicial de registros y variedades.
14. Lentamente Aplique 9 incrementos de 1,1 libras (0.5 kg) o similar en el extremo de la viga. Hacer una pausa en cada paso y permite mediciones se estabilice antes de registrar las lecturas.
15. Lentamente Aplique 9 decrementos de 1,1 libras (0.5 kg) o similar. Hacer una pausa en cada paso y permite mediciones se estabilice antes de registrar las lecturas.
16. Desconecte galgas extensiométricas de indicador de presión y apagar el indicador.
17. Trama de la cepa en el calibrador longitudinal frente a la cepa en el calibre transversal. La pendiente de esta recta corresponde al cociente de Poisson, v.
18. Determinar la pendiente de la mejor línea de ajuste de la trama de tensión vs deformación longitudinal, que es igual al módulo de Young, E.
19. Comparar los valores de E y v con valores previamente establecidos o publicados (en general, habrá un intervalo de valores en lugar de un único valor discreto).

Los datos deben importar o transcrito en una hoja de cálculo para fácil manipulación y graficar. Los datos recogidos se muestran en la tabla 1.

Como el calibrador de tensión de roseta no está alineado con los ejes principales de la viga, las cepas de roseta deban introducir en las ecuaciones para ε_1,2 (ecuación 9) y ε (EC. 10) para calcular las tensiones principales, dando por resultado los datos mostrados en la tabla 2. La tabla muestra que el ángulo entre la tensión medida y las tensiones principales es 0.239 radianes o 13,7 °. Tenga en cuenta que la tensión principal máxima es positiva, correspondiente a una gran tensión extensible longitudinalmente; la tensión principal mínima es negativa, correspondiente a una tensión a la compresión transversal más pequeña. La relación entre las cepas principales máximas y mínimas corresponde al cociente de Poisson, que se muestra en la última columna y promedios sobre 0.310.

	Carga	Calibre 1	Calibre 2	Calibre 3	Calibre 44
Paso	(Lbs)	ΜΕ	ΜΕ	ΜΕ	ΜΕ
1	0.00	1	1	1	0
2	1.10	83	56	-21	-87
3	2.21	163	115	-41	-171
4	3.31	243	171	-62	-254
5	4.42	325	228	-83	-338
6	5.52	400	280	-104	-423
7	6,62	485	338	-122	-501
8	7,73	557	386	-143	-589
9	8.83	634	442	-163	-665
10	9.93	714	502	-184	-741
11	8.83	637	445	-162	-664
12	7,73	561	391	-142	-584
13	6,62	483	335	-123	-506
14	5.52	406	281	-102	-423
15	4.42	323	227	-83	-339
16	3.31	245	171	-62	-256
17	2.21	164	115	-41	-170
18	1.10	83	56	-21	-87
19	0.00	1	0	1	2

Tabla 1: Tensiones en la barra de aluminio.

Gage Factor	1	2	3	Esfuerzo máximo Principal	Mínimo. Tensión principal	Ángulo de	Cociente de Poisson
Fase de carga	ΜΕ	ΜΕ	ΜΕ	(EC. 9)	(EC. 9)	(EC. 10)	(EQ. 7)
1	1	1	1	1	1	0	0
2	83	56	-21	89	-26	-0.223	0.297
3	163	115	-41	176	-55	-0.243	0,311
4	243	171	-62	263	-82	-0.242	0.312
5	325	228	-83	351	-109	-0.240	0,311
6	400	280	-104	432	-136	-0.240	0.314
7	485	338	-122	523	-160	-0.237	0.307
8	557	386	-143	600	-186	-0.236	0.310
9	634	442	-163	684	-213	-0.238	0.312
10	714	502	-184	773	-242	-0.242	0.314
11	637	445	-162	688	-213	-0.239	0.309
12	561	391	-142	605	-186	-0.237	0.308
13	483	335	-123	520	-161	-0.236	0.309
14	406	281	-102	437	-133	-0.234	0.303
15	323	227	-83	349	-109	-0.241	0.313
16	245	171	-62	264	-81	-0.238	0.308
17	56°	115	-41	177	-54	-0.239	0.302
18	83	56	-21	89	-26	-0.223	0.297
19	1	0	1	2	0	0.000	0.000
					Promedio	-0.239	0.310

Tabla 2: Principales cepas y el ángulo de inclinación.

Las cepas principales máximas y mínimas de la tabla 2 se representan gráficamente en la figura 5, que muestra tendencias muy lineales (R² = 0.999) para relación de Poisson. El valor obtenido para la relación de Poisson (0.31), que corresponde a la pendiente de la línea, está muy cerca de las 0.30 en la mayoría de las referencias para el aluminio y otros metales.

Figura 5 : Principal filtrar datos de la pendiente de la línea entre el esfuerzo principal máximo y mínimo, que corresponde al cociente de Poisson.

Una buena interpretación física dato roseta cepa gage puede obtenerse de trazar las principales cepas en un círculo de Mohr (Fig. 6). Nota que las tres medidas, se muestra a continuación para el caso de la carga máxima de 7,4 libras, corresponden a tres puntos en el círculo a 90 º, a partir de un ángulo de unos 27.4º (o 2Φ) en sentido antihorario desde el eje x.

Figura 6 : Significado físico de las lecturas de roseta de cepa se muestra en el círculo de Mohr para deformación.

La tabla 3 muestra las cargas, los resultados de la principal tensión extensible de gage solo en la parte inferior de la viga (Gage 4, que está en compresión), la relación entre la parte inferior y superior tensiones principales máximas, la tensión de módulo EC. (11) y de Young (E) como la relación de la tensión de la ecuación (11) dividida por la tensión de la ecuación (9). En la tabla 3, módulo de Young se calcula como ksi 10147 tomando el promedio de los módulos calculados para los 15 pasos de carga intermedia.

	Carga	Max. Principales. Cepa	Máximo Principal Stress	Tensión Principal de min	Tensión de flexión	Jóvenes ' módulo
Fase de carga	Libras.	ΜΕ	KSI	KSI	PSI	KSI
1	0.00	1	10	9	0	0
2	1.10	89	886	0	882	9945
3	2.21	176	1765	0	1763	9991
4	3.31	263	2630	0	2645	10058
5	4.42	351	3513	0	3526	10038
6	5.52	432	4324	0	4408	10195
7	6,62	523	5230	0	5290	10113
8	7,73	600	6001	0	6171	10283
9	8.83	684	6843	0	7053	10307
10	9.93	773	7726	0	7935	10269
11	8.83	688	6877	0	7053	10256
12	7,73	605	6051	0	6171	10198
13	6,62	520	5204	0	5290	10165
14	5.52	437	4368	0	4408	10091
15	4.42	349	3494	0	3526	10092
16	3.31	264	2644	0	2645	10004
17	2.21	177	1770	0	1763	9960
18	1.10	89	886	0	882	9945
19	0.00	2	19	0	0	0
					Promedio	10147

Tabla 3: Cálculo del módulo de elasticidad (E).

Los datos e también se grafica en la figura 7, que indica una excelente relación lineal (alta R²) entre la tensión y la tensión y una pendiente de aproximadamente 10.147 ksi. La diferencia entre el módulo de la tabla 3 y figura 6 se presenta debido a que los cálculos de la pendiente en la figura 6 requieren que la intercepción de pasar por cero. Las magnitudes comparan muy favorablemente (error menor al 1,5%) con valores publicados de E de aluminio 6061T6, que generalmente se da como 10.000 ksi.

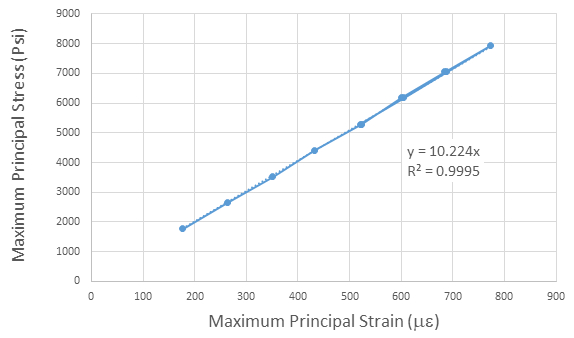
Figura 7 : Pendiente de la línea de tensión máxima y tensión máxima es módulo de Young.

Finalmente, por la refundición de las Eqs. (5) y (6) en:

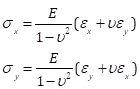(EC. 12)

podemos calcular las tensiones principales usando círculo de Mohr. Para el caso del paso correspondiente a 6,61 libras de carga, las principales cepas de (634,-189) conducen a tensiones principales de (7.34, 0.00) ksi (Fig. 8). Aunque aquí los cálculos se realizaron utilizando correctamente las expresiones para el esfuerzo, los resultados indican que a lo largo del eje principal, la tensión en la dirección perpendicular es cero (o muy cerca de ella), correspondiente al caso de carga uniaxial. Los valores de tensión en un ángulo de 2Φ = 0,40 radianes son (6.50, 2.82) ksi.

Figura 8 : Círculo de Mohr para esfuerzo plano para el caso de una carga de 7,34 libras.

En este experimento se midieron dos constantes materiales fundamentales: el módulo de elasticidad (E) y cociente de Poisson (v). Este experimento demuestra cómo medir estas constantes en un entorno de laboratorio usando un medidor de tensión de la roseta. Los valores obtenidos experimentalmente coincidir bien con los valores publicados de 10.000 ksi y 0.3, respectivamente. Estos valores son clave en la aplicación de la teoría de la elasticidad para diseño de ingeniería, y esta técnica experimental descrita son típicos de los que se utilizan para la obtención de constantes de materiales. Para obtener estos valores, gran debe tener cuidado tanto utilización de instrumentación de alta resolución y procedimientos de calibración trazable. En particular, el uso de cepa gage-dispositivos y sistemas de adquisición de datos digitales de 16 a 24 bits son parte integral para el éxito y la calidad de tales experimentos.

Hoy en día, hay otros métodos para determinar el módulo de Young de un material, incluyendo métodos de propagación de la onda (método de pulso eco ultrasónico) y nanoindentación. Una de las ventajas de utilizar la propagación de la onda es que es uno de los métodos no destructivos de medición módulo de Young, mientras que nanoindentación y uso de un medidor de tensión de roseta son métodos más invasivos.

El diseño de cualquier producto de ingeniería, desde una tostadora a un rascacielos, requiere el uso de modelos analíticos eficaces para mejorar y optimizar el diseño. La teoría de la elasticidad es la base de la mayoría de los modelos utilizados en el diseño de ingeniería civil y se basa en el establecimiento de varias constantes.

Los modelos analíticos son necesarios cuando se construirá sólo una simple (o muy pocos) repeticiones. Como el costo y el rendimiento de la estructura dependen el resultado de esos análisis, y esos análisis, a su vez, dependen de tener sólidos valores para las propiedades del material, pruebas como las descritas deben ejecutar para asegurar la calidad y control de calidad aseguramiento en el proceso de construcción. Por ejemplo:

• En la elección de una fachada de un edificio, el arquitecto debe tener cuidado diseñar un envolvente resistente al agua. La impermeabilidad de un fachada de ladrillo depende mantener el mortero entre los ladrillos sin fisuras, entre otros factores. Si se agrieta el mortero, agua penetran y causan problemas de humedad que serán muy costosos arreglar y corrosión. Para determinar cuánta fuerza puede resistir el mortero antes de las grietas, necesitamos una teoría y sus constantes asociados. El ingeniero estructural y arquitecto debe trabajar juntos para determinar qué cargas la voluntad fachada ver (uno mismo-peso, viento, conducción de la lluvia, etc.) y cómo cada opción de diseño llevará a cabo en esas condiciones. Sólo entonces puede un mortero con las características apropiadas debe ser elegido.
• En la construcción de un edificio, como el Burj Dubai, la constructora debe prestar mucha atención a mantener el nivel de pisos. Conforme avanza la construcción, si los tamaños de las columnas y las paredes son diferentes, algunos de estos elementos pueden acortar (tensión) más que otros como avanza la construcción y más peso (tensión) se agrega. Para obtener pisos planos en el final de la construcción, la constructora tendrá que hacer ajustes a la altura de las columnas y muros en los pisos inferiores - las plantas bajas no nivel durante las fases iniciales de la construcción pero deben ser plana en el extremo. Para calcular cómo hacer estos ajustes correctamente, la empresa constructora contratará un ingeniero estructural para proporcionar datos en columna diferencial y alturas de pared. El ingeniero deberá utilizar constantes materiales para realizar estos cómputos.
• En el diseño de una lata de soda, un fabricante debe reducir al mínimo el espesor de la pared de aluminio, como el aluminio es un material muy caro. Para optimizar la forma y dimensiones de las latas, el fabricante debe determinar qué condiciones de carga son importantes; condiciones de transporte y almacenamiento pueden ser más exigente que el consumidor beber de él. Muchas de estas condiciones será difícil y costoso de replicar dentro de un programa de pruebas experimental; el fabricante podrá optar por hacer un montón de análisis para optimizar las dimensiones de la lata antes de pasar a la fase de prototipo. Este procedimiento es lo que Boeing siguió en el desarrollo del Dreamliner de Boeing (Boeing 787). Para hacer estos estudios, propiedades de los materiales deben ser conocido y la teoría adecuada seleccionada.