Materialkonstanten

Quelle: Roberto Leon, Department of Civil and Environmental Engineering, Virginia Tech, Blacksburg, VA

Im Gegensatz zu der Produktion von Autos oder Toaster, wo Millionen identischer Kopien gemacht und umfangreiche Prototyp testen ist möglich, ist jeder hoch-und Tiefbau-Struktur einzigartig und sehr teuer (Abb. 1) zu reproduzieren. Daher müssen Bauingenieure ausgiebig auf analytische Modellierung, ihre Strukturen zu entwerfen verlassen. Diese Modelle sind vereinfachte Abstraktionen der Realität und dienen zur Überprüfung, dass die Leistungskriterien, insbesondere in Bezug auf Festigkeit und Steifigkeit, nicht verletzt werden. Um diese Aufgabe zu erfüllen, benötigen Ingenieure zwei Komponenten: (a) eine Reihe von Theorien, die machen Strukturen Lasten, d.h. die Reaktion auf, wie die Kräfte und Verformungen zusammenhängen und (b) eine Reihe von Konstanten, die innerhalb dieser Theorien zu unterscheiden wie Materialien (z.B. Stahl und Beton) unterscheiden sich in ihrer Antwort.

Abbildung 1: World Trade Center (NYC) Verkehrsknotenpunkt.

Die meisten Konstruktion verwendet heute lineare elastischen Prinzipien, um Kräfte und Verformungen in Strukturen zu berechnen. In der Theorie der Elastizität sind mehrere Materialkonstanten musste das Verhältnis zwischen Spannung und Dehnung zu beschreiben. Stress wird definiert als Kraft pro Flächeneinheit, während Belastung als die Veränderung der Dimension definiert ist bei einer Krafteinwirkung, geteilt durch die ursprüngliche Größe der Dimension Umkippen. Die beiden am häufigsten dieser Konstanten sind der Elastizitätsmodul (E), bezieht sich die Belastung auf die Belastung und Poisson Verhältnis (ν), die das Verhältnis der seitlichen längs belastet ist. Dieses Experiment wird die typische Ausrüstung in einem Bau-Materialien-Labor zur Messung der Kraft (oder Stress) einführen und Verformung (oder Belastung), und verwenden sie zum Messen von E und ν einer typischen Aluminium-Bar.

Das häufigste Modell für die Analyse ist lineare Elastizität (Hooke Gesetz), die postuliert, dass Änderungen in Kraft (F) Veränderungen der Dimension (Δ) direkt proportional sind. In seiner einfachsten Form bei einachsiger Belastung beziehen sich Kraft und Verformung von einer Konstante (E) oder der e-Modul:

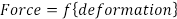(GL. 1)

(GL. 2)

(GL. 3)

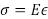(GL. 4)

Wie in den obigen Gleichungen beschrieben, sind die Belastungen Mengen, im Gegensatz zu echten Mengen engineering. Wahre Mengen erfordern eine kleinen, aber endlichen Änderungen in lokalen Dimensionen Messen, die auftreten, wenn die Kräfte erhöht werden. Dieses Kunststück ist experimentell, sehr schwer zu erreichen, auch mit der jüngsten Fortschritte in der berührungslosen Messtechniken. Für diese Berechnungen kann man davon ausgehen, diese Änderungen sind vernachlässigbar, und verwenden Sie die ursprüngliche Fläche (A₀) und Länge (L₀).

Um den Elastizitätsmodul aus den obigen Gleichungen zu ermitteln, muß man haben, eine Möglichkeit, die Änderungen in Kraft und Länge bestimmen, wie eine Probe geladen wird. In einem groben Experiment könnte man eine Personenwaage und ein Lineal verwenden, um diese Aufgaben zu erledigen. Man könnte zuerst ein dickes Gummiband nehmen, seine Dimensionen zu messen und markieren Sie zwei Punkte auf dem Band, getrennt durch einen Zoll. Man könnte als nächstes legen Sie einen offenen Behälter auf eine Waage und Wasser hinzufügen, bis die Lesung zehn Pfund ist. Man könnte dann unterbrechen den Behälter mit dem Gummiband und Messen, wie viel die beiden Marken getrennt haben. Diese Messung wird geben Sie uns die Daten, die zur Berechnung E für Kautschuk, da haben wir alle Werte für E in Eqs lösen musste. (2) bis (4). Es wird jedoch sehr große Unsicherheiten und Fehler in Verbindung mit der Messung aufgrund der sehr groben Messgerät. Da das Ausmaß der Belastung benötigt für gemessen werden typische Konstruktion sind Materialien in der Größenordnung von 1 x 10^-6, weit mehr präzise Messgeräte sind notwendig, um Materialkonstanten experimentell zu bestimmen. Für die gängigsten Anwendungen basieren diese Messungen auf elektrischen Widerstand Dehnungsmessstreifen. Da diese Geräte in den folgenden Videos verwendet werden, wird eine Beschreibung ihrer betrieblichen Grundsätze weiter gegeben.

DMS ist eine lange Schleife Draht eingebettet auf einer Trägermatrix (Abb. 2). DMS wird auf das Material getestet mit einem hochfesten Epoxy geklebt. Wenn das Material verformt ist, ändert sich die Drähte in der Länge und ihren Widerstand wird dadurch etwas ändern. Wenn die Gage als Teil einer Wheatstone-Brücke-Schaltung eingefügt wird, können diese Änderungen als Änderungen in der Spannung erkannt werden. Das Aufkommen der digitalen Messsystemen hat erheblich reduziert Hintergrundgeräusche und andere Fehlerquellen innerhalb der Schaltung, und verbessert die Präzision in welcher, die Spannung Änderungen heute gemessen werden können. DMS ist kalibriert mit eine Konstante bekannt als Gage Faktor, so dass seine Ausgabe linear zur Belastung für einen bestimmten Dehnungsbereich unter einen bestimmten Spannungseingang zusammenhängt.

DMS misst die Belastung nur in eine Richtung. Um den vollständigen Zustand der Spannung an einem Punkt auf einer Fläche zu erhalten, eine Rosette strain Gage, die aus drei Dehnungsmessstreifen ausgerichtet auf 45° zu einem anderen benötigt wird (Abb. 3). Mit diesen Messungen in drei verschiedene Richtungen kann der gesamte Staat von Stress auf einer Fläche definiert werden, durch den Einsatz von Prinzipien wie Mohrs Kreis, um maximal- und Minimalwerte hauptdehnungen und Spannungen zu berechnen.

Abbildung 2 : DMS.

Abbildung 3 : Rosette DMS.

Messungen von Gewalt sind auch mit Dehnungsmessstreifen vorgenommen; Allerdings sind in der Regel diese Messungen in einer Vollbrücke Konfiguration (d. h. die internen Widerstände in einer Wheatstone-Brückenschaltung werden durch externe aktive DMS ersetzt) wodurch ein Gerät namens eine Wägezelle. Die Wägezelle selbst ist in der Regel einen dicken, hochfeste Stahl Zylinder mit zwei DMS längs eingebaut und zwei quer installiert, um die Auswirkungen der Poisson Verhältnis zu beseitigen. Die Kalibrierung einer Wägezelle erfordert, dass Tote Gewichte verwendet werden, so dass die Ausgangsspannung der Schaltung auf eine gegebene Belastung bezogen werden kann. In den Vereinigten Staaten kalibriert die National Institute of Science and Technology (NIST) Wägezellen bis auf 5 Millionen kN mit Toten Gewichten und hebelmechanismen. Alle Wägezellen verwendet in den USA müssen auf diese Kalibrierung Quelle rückverfolgt werden können. In der Praxis ist Rückverfolgbarkeit bedeutet, die Zelle A laden vom NIST mit Toten Gewichten, an andere Laboratorien genommen und installiert in Serie mit Wägezelle B. kalibriert. Schließlich ist die Wägezelle B kalibriert basierend auf dem Vergleich der Ausgabe an den Ausgang der Wägezelle A. Alle Wägezellen müssen in regelmäßigen Abständen kalibriert werden, um sicherzustellen, dass sie einwandfrei funktionieren.

Die Wägezelle ist in der Regel auf einer Universalprüfmaschine (UTM) installiert. Eine UTM besteht aus einem selbst reagierenden Rahmen mit zwei Schrauben-Spalten, die von einem Motor (Abb. 4) aktiviert sind. Durch eine Probe in die UTM-Griffe Spann- und Drehen der Schraube-Spalte, so dass die Kreuzkopf bewegt sich nach oben, werden Zugkräfte in der Probe eingeführt. Die einwirkende Kraft wird durch die Wägezelle gemessen, die in Serie mit der Probe installiert ist. Auf der anderen Seite, wenn Platten anstelle von Zug-Griffe installiert sind und die Schraube Spalten werden nach unten verschoben, Druckkräfte werden eingeführt in den Prüfling (d. h. konkrete Zylinder zu testen).

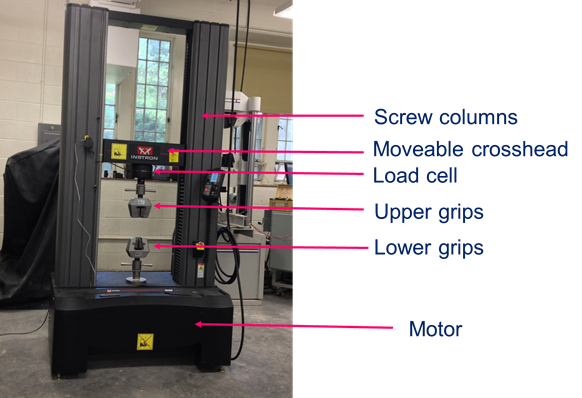
Abbildung 4 : Universalprüfmaschine.

Nun, wie Dehnung und Kraft messen nachgewiesen wurde, wird eine allgemeinere Behandlung der Theorie der Elastizität diskutiert werden. Blick auf eine generische Stück einer Struktur Belastungen ausgesetzt, kann man schreiben, Gleichungen des Gleichgewichts für Kräfte und Momente auf allen Achsen.

Daraus ergeben sich eine Reihe von Gleichungen für normale (ε) und Schere (γ) Stämme des Formulars:

(GL. 5)

(GL. 6)

Sechs Gleichungen dieser Art, drei für normale Belastungen (ε_Xund ε_y ε_Z) und drei für Scheren Stämme (γ_Xy, γ_Yz und γ_Zx) sind notwendig, um die globale Verformungen zu etablieren. Diese Gleichungen enthalten drei Materialkonstanten: der Elastizitätsmodul von Elastizität (E), Poisson Verhältnis (ν) und der Schubmodul (G). Wie in der obigen Gleichung dargestellt, ist der Schubmodul die Veränderung in eckigen Verformung einer Scherbeanspruchung oder Oberfläche Traktion gegeben. Poisson Verhältnis ist definiert als:

(GL. 7)

Es kann gezeigt werden, dass:

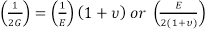= G (GL. 8)

Nur zwei der drei Konstanten müssen also ermittelt werden, um alle drei zu definieren. Es gibt zahlreiche andere abgeleiteten Konstanten, in Elastizitätstheorie, verwendet werden, die aus diesen Messungen abgeleitet werden können. Beispielsweise ist das Kompressionsmodul (B) oder die relative Änderung des Volumens eines Körpers durch eine Einheit Druck- oder Zugkräfte Stress handeln gleichmäßig über seine Oberfläche produziert:

Von Eqs. (5) und (6), man kann den Zustand von Stress und Belastung auf einer Fläche bestimmen, wenn mindestens drei unabhängige Dehnungsmessungen vorgenommen werden. Wenn Rosette DMS, hat drei DMS bei 45° zueinander (Abb. 3) anstelle einer einzigen längs Gage verwendet wird, dann findet die maximalen und minimalen hauptdehnungen (ε₁, ε-₂) und den Winkel (Φ) zwischen den gemessenen Stämmen man und die hauptdehnungen von Mohrs Kreis.

Für rechteckige Rosette DMS, wie gezeigt in Abb. 3 wo die DMS bei 45 Grad zueinander sind:

(GL. 9)

Φ =

Das Spektrum der Stämme über die linearen elastische Beziehungen halten liegt zwischen null und die proportionale Grenze des Materials. In diesem Experiment, das Aluminium verwendet wird, wird die Palette der Stämme deutlich unter dieser Grenze gehalten werden.

Wir verwenden eine einfache Auslegerbalken instrumentiert mit Dehnungsmessstreifen zur Veranschaulichung der Konzepte der wichtigsten Belastungen und Beanspruchungen und die Berechnung der Elastizitätsmodul (E) und Poisson Verhältnis (ν).  Die Auslegerbalken wird schrittweise mit einem Satz von Gewichten und die entsprechenden Änderungen in den Stamm aufgenommen geladen werden.  Die entsprechenden Spannungen können aus der einfachen Biegung Stress Gleichung berechnet werden:

(GL. 11)

wo M ist der Zeitpunkt (oder Kraft multipliziert mit der Hebelarm), c ist die Entfernung von den Schwerpunkt auf die extreme Faser in den Strahl über seine tiefe (), und ich ist das Trägheitsmoment, gegeben durch wo b ist die Lichtstrahlbreite und t ist seine Stärke.

E-Modul Elastizität und Poisson Verhältnis

Es wird hierin auszugehen, dass Studenten in der Nutzung und Sicherheitsvorkehrungen erforderlich, um eine universelle Prüfmaschine betreiben ausgebildet wurden.

1. Erhalten eine rechteckigen Aluminium bar (12 Zoll x 1 Zoll x ¼ in.); ein Aluminium 6061 T6xxx oder stärker wird empfohlen. Ein Loch gebohrt ca. 1 Zoll von einem Balkenende als eine Ladestelle dienen.
2. Markieren Sie eine Position auf dem Balken etwa 8,0 Zoll von der Mitte der Bohrung auf der Oberseite des Balkens. Zeichnen Sie Ausrichtungsmarken für die Rosette Dehnungsmessstreifen und stellen Sie sicher, dass die Achsen der Rosette zur Längsachse des Strahls in einem kleinen Winkel (etwa 10° bis 15°) geneigt sind.
3. Markieren Sie eine ähnliche Position auf der unteren Oberfläche des Trägers. Einzelnen DMS hier installiert werden und sollte mit der Längsachsen des Strahls ausgerichtet werden.
4. Messen Sie die Breite (b) und Dicke (t) der Bar sorgfältig mit Bremssättel. Führen Sie drei Wiederholungen an drei verschiedenen Standorten, einen guten Durchschnitt der Dimensionen zu erhalten. Aus diesen Messungen berechnen Sie das Trägheitsmoment (I) und der Abstand von der neutralen Achse an die extreme Faser des Balkens (c t/2 =).
5. Erhalten eine Rosette DMS mit einem Sensor Raster von ca. ¼ Zoll lang 1/8 mm breit auf jede Gage und eine ähnliche einzelne Belastung zu bewerten. Hinweis: die kalibrierfaktoren (oder Gage Faktor) für die DMS.
6. Um die Rosette DMS zu installieren, zuerst Entfetten Sie und reinigen Sie die Oberfläche sorgfältig; Schleifen Sie die Oberfläche mit immer feineren Schleifpapier, bis eine sehr glatte Oberfläche erzielt wird; Reinigen Sie die Oberfläche mit einem Neutralisator; und kleben Sie die DMS nach den Vorgaben des Herstellers. Lassen Sie den Kleber richtig zu heilen, bevor Sie fortfahren.
7. Testen Sie den Widerstand des DMS (in der Regel 120 Ohm) und ihre aktuelle Leckage an der Bar (idealerweise größer als 5 mOhm Widerstand), bevor Sie fortfahren.
8. Wiederholen Sie die Schritte 1.5 bis 1.7 für die einzelnen Gage auf der unteren Fläche installiert werden.
9. Legen Sie die Probe in der Cantilever-Apparat und entsprechend zu sichern.
10. Schließen Sie die Dehnungsmessstreifen an ein Aufnahmegerät, wie z. B. ein Vishay P3-Stamm-Indikator. Stellen Sie sicher, dass die Verdrahtung korrekt gemäß den Stamm-Indikator-Anweisungen ist und dass Sie wissen, welcher Kanal zu jeder DMS entspricht.
11. Geben Sie die entsprechende Gage Faktoren für jede Gage in der Anzeige.
12. Überprüfen Sie die Gerätekalibrierung durch Eingabe einer bekannten Spannung, die zu einer Lesung des 5000με mit dem Gage-Faktor von 2,00 führt.
13. Rekord anfangsbelastung und Stämme.
14. Langsam gelten 9 Schritten von 1,1 lbs (0,5 kg) oder ähnliches Ende Strahl. Anhalten bei jedem Schritt und Messungen zur Stabilisierung vor der Aufnahme der Messwerte zu ermöglichen.
15. Langsam gelten 9 dekrementiert 1,1 lbs (0,5 kg) oder ähnliches. Anhalten bei jedem Schritt und Messungen zur Stabilisierung vor der Aufnahme der Messwerte zu ermöglichen.
16. Stamm-Indikator trennen Sie DMS und schalten Sie die Anzeige aus.
17. Zeichnen Sie die Dehnung in der longitudinalen Gage vs. die Dehnung in der transversalen Gage. Die Steigung dieser Linie entspricht Poissons Verhältnis, V.
18. Bestimmen Sie die Steigung der beste Fit Linie vom Grundstück des Druckes vs. längs Stamm, der Elastizitätsmodul, E. entspricht
19. Vergleichen Sie Ihre Werte E und v mit bereits etablierten oder veröffentlichten Werte (in der Regel werden eine Reihe von Werten gegeben, anstatt einen diskreten Einzelwert).

Die Daten sollten importiert oder transkribiert in eine Tabellenkalkulation für einfache Handhabung und grafisch darzustellen. Die erhobenen Daten ist in Tabelle 1 dargestellt.

Weil die Rosette DMS nicht mit den Hauptachsen des Strahls ausgerichtet ist, müssen die Rosette Stämme in die Gleichungen für ε_1,2 (GL. 9) und ε (GL. 10) oben hauptdehnungen, wodurch die Daten in Tabelle 2 dargestellte Berechnung eingegeben werden. Die Tabelle zeigt, dass der Winkel zwischen der gemessenen Spannung und die Hauptspannungen 0,239 Bogenmaß oder 13,7 ° geht. Beachten Sie, dass die maximale Dehnung der wichtigsten positiven, längs, eine große Zugbelastung entspricht; die minimale wichtigste Sorte ist negativ, ein kleiner quer Druckspannung entspricht. Das Verhältnis zwischen der minimalen und maximalen hauptdehnungen entspricht Poisson Verhältnis, das auf die letzte Spalte angezeigt wird und im Durchschnitt über 0,310.

	Last	Gage 1	Gage 2	Gage 3	Gage 44
Schritt	(Lbs.)	ΜΕ	ΜΕ	ΜΕ	ΜΕ
1	0.00	1	1	1	0
2	1.10	83	56	-21	-87
3	2.21	163	115	-41	-171
4	3.31	243	171	-62	-254
5	4.42	325	228	-83	-338
6	5.52	400	280	-104	-423
7	6.62	485	338	-122	-501
8	7.73	557	386	-143	-589
9	8,83	634	442	-163	-665
10	9.93	714	502	-184	-741
11	8,83	637	445	-162	-664
12	7.73	561	391	-142	-584
13	6.62	483	335	-123	-506
14	5.52	406	281	-102	-423
15	4.42	323	227	-83	-339
16	3.31	245	171	-62	-256
17	2.21	164	115	-41	-170
18	1.10	83	56	-21	-87
19	0.00	1	0	1	2

Tabelle 1: Stämme in Aluminium Bar.

Gage-Faktor	1	2	3	Maximale Principal Belastung	Minimum reduziert. Principal-Stamm	Winkel	Poisson Verhältnis
Laststufe	ΜΕ	ΜΕ	ΜΕ	(GL. 9)	(GL. 9)	(GL. 10)	(GL. 7)
1	1	1	1	1	1	0	0
2	83	56	-21	89	-26	-0.223	0.297
3	163	115	-41	176	-55	-0.243	0.311
4	243	171	-62	263	-82	-0.242	0.312
5	325	228	-83	351	-109	-0.240	0.311
6	400	280	-104	432	-136	-0.240	0.314
7	485	338	-122	523	-160	-0.237	0.307
8	557	386	-143	600	-186	-0.236	0,310
9	634	442	-163	684	-213	-0.238	0.312
10	714	502	-184	773	-242	-0.242	0.314
11	637	445	-162	688	-213	-0.239	0.309
12	561	391	-142	605	-186	-0.237	0.308
13	483	335	-123	520	-161	-0.236	0.309
14	406	281	-102	437	-133	-0.234	0.303
15	323	227	-83	349	-109	-0.241	0.313
16	245	171	-62	264	-81	-0.238	0.308
17	164	115	-41	177	-54	-0.239	0.302
18	83	56	-21	89	-26	-0.223	0.297
19	1	0	1	2	0	0.000	0.000
					Durchschnitt	-0.239	0,310

Tabelle 2: Principal Stämme und Neigungswinkel.

Die maximalen und minimalen hauptdehnungen aus Tabelle 2 sind in Abb. 5 sehr linearen Trends zeigt geplottet (R² = 0,999) für Poissons-Verhältnis. Der Wert für die Poisson Verhältnis (0,31), das entspricht der Steigung der geraden ist sehr nah an die 0,30 gegeben in den meisten Referenzen für Aluminium und anderen Metallen.

Abbildung 5 : Principal belasten Daten zeigen die Steigung der Linie zwischen maximalen und minimalen wichtigste Sorte, die Poisson Verhältnis entspricht.

Eine gute körperliche Interpretation der Rosette Strain Gage Daten kann vom Plotten die hauptdehnungen auf einem Mohr-Kreis (Abb. 6) gewonnen werden. Beachten Sie, dass die drei Messungen, für den Fall der Maximallast von 7,4 Pfund hier gezeigten drei Punkte im Kreis an 90° zueinander entsprechen, beginnend in einem Winkel von ca. 27.4º (oder 2Φ) gegen den Uhrzeigersinn von der x-Achse.

Abbildung 6 : Physikalische Bedeutung der Sorte Rosette Lesungen auf Mohrs Kreis für Belastung gezeigt.

Tabelle 3 zeigt die Belastungen, die Ergebnisse für die wichtigsten Zugbelastung aus dem einzigen Gage auf der Unterseite des Balkens (Gage 4, die bei der Kompression ist), das Verhältnis zwischen der unteren und oberen maximale Hauptspannung, den Stress aus GL. (11) und Youngs Modulus (E) als das Verhältnis zwischen der Spannung von GL. (11) geteilt durch die Belastung von GL. (9). In Tabelle 3 ist des Elastizitätsmoduls als 10147 Ksi unter dem Durchschnitt der Moduli berechnet für die 15 mittlere Beladung Schritte berechnet.

	Last	Max. Wichtigsten. Stamm	Max Principal Stress	Min Haupt Stress	Biegespannung	Junge "Modulus
Laststufe	Lbs.	ΜΕ	ksi	ksi	PSI	ksi
1	0.00	1	10	9	0	0
2	1.10	89	886	0	882	9945
3	2.21	176	1765	0	1763	9991
4	3.31	263	2630	0	2645	10058
5	4.42	351	3513	0	3526	10038
6	5.52	432	4324	0	4408	10195
7	6.62	523	5230	0	5290	10113
8	7.73	600	6001	0	6171	10283
9	8,83	684	6843	0	7053	10307
10	9.93	773	7726	0	7935	10269
11	8,83	688	6877	0	7053	10256
12	7.73	605	6051	0	6171	10198
13	6.62	520	5204	0	5290	10165
14	5.52	437	4368	0	4408	10091
15	4.42	349	3494	0	3526	10092
16	3.31	264	2644	0	2645	10004
17	2.21	177	1770	0	1763	9960
18	1.10	89	886	0	882	9945
19	0.00	2	19	0	0	0
					Durchschnitt	10147

Tabelle 3: Berechnung der Elastizitätsmodul (E).

Die Daten für E ist auch in Abb. 7, kennzeichnet eine ausgezeichnete lineare Beziehung (hohe R²) zwischen Spannung und Dehnung und einer Neigung von ca. 10.147 Ksi aufgetragen. Der Unterschied zwischen der e-Modul aus Tabelle 3 und aus Abb. 6 entsteht, weil die Berechnungen für die Neigung in Abb. 6 verlangen, dass die Schnittkante durch Null zu gehen. Die Größen vergleichen sehr günstig (Fehler weniger als 1,5 %) mit veröffentlichten Werte von E für 6061T6 aus Aluminium, die in der Regel als 10.000 Ksi gegeben ist.

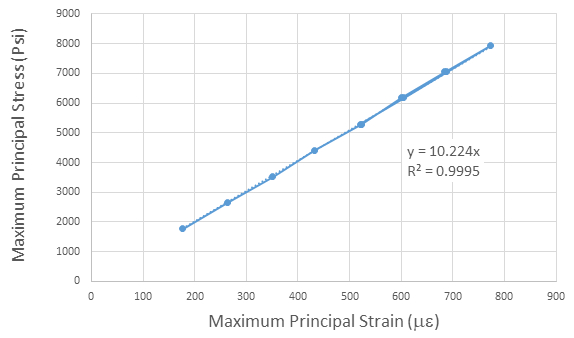
Abbildung 7 : Die Steigung der Linie der Maximalspannung vs. Maximale Dehnung ist des Elastizitätsmoduls.

Zu guter Letzt durch eine Neufassung Eqs. (5) und (6) in:

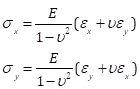(GL. 12)

Wir können die Hauptspannungen mit Mohrs Kreis berechnen. Für den Fall der Schritt entspricht 6,61 lbs der Last, die hauptdehnungen (634,-189) führen zu der Hauptspannungen (7.34, 0,00) Ksi (Abb. 8). Obwohl hier die Berechnungen durchgeführt werden mit den Ausdrücken für Flugzeug Stress, die Ergebnisse korrekt anzugeben, dass entlang der Hauptachse ist die Spannung in der senkrechten Richtung NULL (oder sehr nahe daran), entsprechende auf den Fall von einachsigen laden. Die Spannungswerte in einem Winkel von 2Φ = 0,40 Bogenmaß sind (6,50, 2,82) Ksi.

Abbildung 8 : Mohrs Kreis für Flugzeug-Stress für den Fall einer 7,34 lbs Last.

In diesem Experiment wurden zwei wesentliche Materialkonstanten gemessen: der Modul von Elastizität (E) und Poisson Verhältnis (V). Dieses Experiment zeigt, wie diese Konstanten in einer Laborumgebung mit Rosette DMS zu messen. Die experimentell ermittelten Werte entsprechen gut mit den veröffentlichten Werten von 10.000 Ksi und 0,3, beziehungsweise. Diese Werte sind der Schlüssel bei der Anwendung der Theorie der Elastizität für Konstruktion, und diese experimentelle Technik beschriebenen sind typisch für diejenigen für den Erhalt der Materialien Konstanten verwendet. Um diese Werte zu erhalten, müssen beide geachtet werden Nutzung der hochauflösenden Instrumentierung und nachvollziehbar Kalibrierverfahren. Insbesondere die Verwendung von Strain Gage-basierten Geräten und digitalen Datenerfassungssysteme von 16 auf 24 Bit sind ein integraler Bestandteil für den Erfolg und die Qualität solcher Experimente.

Heute gibt es andere Methoden zur Bestimmung des Elastizitätsmoduls eines Materials, einschließlich der Welle Ausbreitung Methoden (Ultraschall-Echo-Puls-Methode) und Nanoindentation. Ein Vorteil der Verwendung von Wellenausbreitung ist, dass es eines der Zerstörungsfreie Methoden zur Messung des Elastizitätsmoduls Nanoindentation und Einsatz von DMS Rosette mehr invasiven Methoden sind.

Das Design von technischen Produkten, aus ein Toaster, ein Hochhaus, erfordert die Verwendung von effektiven analytische Modelle zu verbessern und optimieren das Design. Die Theorie der Elastizität ist die Grundlage für die meisten Modelle in hoch-und Tiefbau-Design verwendet und basiert auf die Einrichtung von mehreren Konstanten.

Analytische Modelle sind erforderlich, wenn nur eine einzelne (oder wenige) Wiederholungen gebaut werden. Kosten und Leistung der Struktur das Ergebnis dieser Analysen hängt, und diese Analysen hängen wiederum mit robusten Werte für die Eigenschaften des Materialien müssen Tests wie hier beschrieben ausgeführt werden, um Qualitätskontrolle und Qualität zu gewährleisten Qualitätssicherung in den Bauprozess. Zum Beispiel:

• Bei der Auswahl einer Fassade eines Gebäudes, muss der Architekt eine wasserdichte Hülle Design achten. Die Wasserdichtigkeit der ein Backsteingebäude Fassade kann auf die Erhaltung des Mörtels zwischen den Steinen ungerissen, neben anderen Faktoren abhängen. Wenn der Mörtel Risse, wird Wasser eindringen und verursachen Korrosion und Feuchtigkeitsprobleme, die sehr teuer zu beheben sein werden. Um wie viel Kraft bestimmen der Mörtel widerstehen kann, bevor es Risse, brauchen wir eine Theorie und seine zugehörigen Konstanten. Der Architekt und strukturellen Ingenieur muss zusammenarbeiten, um festzustellen, was die Fassade wird geladen sehen (Eigengewicht, Wind, Regen usw. fahren) und wie jede Entwurfsoption unter diesen Bedingungen durchzuführen. Nur dann kann ein Mörtel mit den entsprechenden Merkmalen gewählt werden sollte.
• Die Baufirma muss bei der Konstruktion eines hohen Gebäudes, wie dem Burj Dubai, achten auf die Etagen-Niveau zu halten. Fortschreiten der Konstruktion wenn die Größen der Säulen und Wände unterscheiden, können einige dieser Elemente (Stamm) verkürzen mehr als andere als den Baufortschritt und mehr Gewicht (Stress) wird hinzugefügt. Um flache Böden am Ende der Konstruktion zu erhalten, müssen die Baufirma Anpassungen vornehmen, um die Höhe der Säulen und Wände in den unteren Etagen - den unteren Etagen möglicherweise nicht Ebene während der Anfangsphase des Baus sollte jedoch am Ende flach. Um wie richtig diese Anpassungen zu berechnen, wird die Baufirma einen Statiker auf differenzielle Spalte und wandhöhen Angaben einstellen. Der Ingenieur musst Materialkonstanten verwenden, um diese Berechnungen durchzuführen.
• Bei der Gestaltung von einer Cola-Dose muss ein Hersteller die Wanddicke Aluminium, minimieren, da Aluminium ein sehr teures Material ist. Um die Form und die Abmessungen der Dosen zu optimieren, muss der Hersteller zu bestimmen, welche Ladebedingungen wichtig sind; Transport-und Lagerbedingungen möglicherweise anspruchsvoller als des Verbrauchers daraus trinken. Viele dieser Bedingungen werden schwer und teuer, im Rahmen einer experimentellen Testprogramm zu replizieren; der Hersteller kann entscheiden, viel Analyse, können Dimensionen zu optimieren, bevor mit der Prototypen-Phase zu tun. Dieses Verfahren ist was Boeing bei der Entwicklung der Dreamliner (Boeing 787) folgte. Um diese Studien zu tun, müssen Materialeigenschaften bekannt und der entsprechenden Theorie ausgewählt werden.