Constantes de matériau

Source : Roberto Leon, département de génie Civil et environnemental, Virginia Tech, Blacksburg, VA

Contrairement à la production de voitures ou de grille-pains, où des millions d’exemplaires identiques sont faites et essais de prototypes étendue est possible, chaque ouvrage de génie civil est unique et très coûteux à reproduire (Fig.1). Par conséquent, ingénieurs civils doit s’appuyer largement sur la modélisation analytique pour la conception de leurs structures. Ces modèles sont des abstractions simplifiées de la réalité et sont utilisés pour vérifier que les critères de performance, en particulier ceux liés à la résistance et la rigidité, ne sont pas violés. Afin d’accomplir cette tâche, ingénieurs ont besoin de deux pièces : un ensemble de théories qui expliquent comment les structures répondent à des charges, c'est-à-dire, comment les forces et les déformations sont liées et (b) une série de constantes qui différencient dans ces théories comment matériaux (acier et béton) diffèrent dans leur réponse.

Figure 1 : Plaque tournante du transport World Trade Center (New York).

La plupart de conception technique utilise aujourd'hui des principes élastiques linéaires pour calculer les forces et les déformations dans les structures. Dans la théorie de l’élasticité, plusieurs constantes de matériau sont nécessaires pour décrire la relation entre le stress et la fatigue. Stress se définit comme la force par unité de surface, alors que la souche est définie comme le changement de dimension lorsqu’elle est soumise à une force divisée par la grandeur originale de cette dimension. Les deux plus courantes de ces constantes sont le module d’élasticité (E), qui concerne le stress la souche et coefficient de Poisson (ν), c'est-à-dire le rapport entre latéral à déformation longitudinale. Cette expérience va introduire l’équipement typique utilisé dans un laboratoire de matériaux de construction pour mesurer la force (ou stress) et déformation (ou souche) et utilisez-les pour mesurer E et ν d’une barre d’aluminium typique.

Le modèle le plus courant utilisé pour l’analyse est élasticité linéaire (Loi de Hooke), qui postule que les changements en vigueur (F) sont directement proportionnels aux changements de dimension (Δ). Dans sa forme la plus simple en cas d’uniaxiale, force et déformation sont liés par une constante seule (E) ou le module d’élasticité :

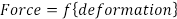(EQ. 1)

(EQ. 2)

(EQ. 3)

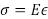(Équation 4)

Tel que décrit dans les équations ci-dessus, la stress et la fatigue sont des quantités, par opposition aux quantités vraies. Vraies quantités exigent un pour mesurer les modifications modestes mais finies dans des dimensions locales qui se produisent lorsque les forces sont augmentées. Expérimentalement, cet exploit est très difficile à accomplir, même avec les progrès récents dans les technologies de mesure sans contact. Pour ces calculs, on peut supposer ces changements sont négligeables et utilisent la zone d’origine (₀) et la longueur (L₀).

Afin de déterminer le module d’élasticité des équations ci-dessus, il faut avoir un moyen de déterminer les changements dans la force et la longueur comme un spécimen est chargé. Dans une expérience brute, on pourrait utiliser un pèse-personne et un dirigeant pour accomplir ces tâches. Tout d’abord, on pourrait prendre une bande de caoutchouc épaisse, mesurer ses dimensions et marquer deux points sur la bande séparés par un pouce. Ensuite, on pourrait placer un récipient ouvert sur une échelle et ajouter de l’eau jusqu'à ce que la lecture soit dix livres. On pourrait alors suspendre le récipient avec de l’élastique et mesurer combien les deux marques ont séparés. Cette mesure nous donnera toutes les données nécessaires pour calculer E pour caoutchouc puisque nous avons toutes les valeurs nécessaires pour résoudre pour E dans les égaliseurs. (2) à (4). Cependant, il y aura des très grandes incertitudes et erreur associée à la mesure en raison du dispositif de mesure très grossière. Étant donné l’ampleur de la déformation nécessaire à mesurer pour construction typique des matériaux sont de l’ordre des appareils de mesure précis 1 x 10^-6, beaucoup plus sont nécessaires pour déterminer les constantes matérielles expérimentalement. Pour les applications de mécanique plus courantes, ces mesures reposent sur des jauges de résistance électrique. Comme ces appareils seront utilisés dans les vidéos suivantes, aura une description de leurs principes de fonctionnement ensuite.

Un extensomètre est un fil long bouclé embarqué sur une matrice de support (Fig. 2). L’extensomètre est collé sur le matériel mis à l’essai avec un époxy de haute résistance. Lorsque le matériau est déformé, les fils vont changer de longueur et leur résistance sera légèrement modifiée en conséquence. Lorsque le gage est inséré dans le cadre d’un circuit en pont de Wheatstone, ces changements peuvent être détectés comme des variations de tension. L’avènement des systèmes de mesure numérique a considérablement réduit les bruits de fond et d’autres sources d’erreur dans le circuit, ce qui améliore la précision quelle tension de modifications peuvent être mesurées aujourd'hui. L’extensomètre est calibré à l’aide d’une constante connue comme un facteur de gage, afin que sa sortie est linéairement liée à la souche pour une gamme de souche quelconque sous une tension donnée d’entrée.

Un extensomètre mesure la souche dans un seul sens. Afin d’obtenir l’état complet du stress à un point sur une surface, une rosette strain gage, qui est composé de trois jauges alignés à 45º à un autre est nécessaire (Fig. 3). Avec ces mesures dans trois directions différentes, l’ensemble de l’état de stress sur une surface peut être défini en utilisant les principes comme cercle de Mohr pour calculer les contraintes et les déformations principales maximales et minimales.

Figure 2 : Extensomètre.

Figure 3 : Extensomètre rosette.

Mesures de force sont également faites avec jauges de contrainte ; Toutefois, ces mesures sont généralement faites dans une configuration en pont complet (c.-à-d., les résistances à l’intérieur dans un Wheatstone pont circuit sont remplacés par les mesureurs d’actifs externes) résultant dans un dispositif appelé un peson. Le peson lui-même est habituellement un cylindre en acier épais et de haute résistance avec deux jauges installés longitudinalement et deux installé transversalement afin d’éliminer les effets du coefficient de Poisson. L’étalonnage d’un peson exige que les poids morts servir afin que la tension nominale du circuit peut être liée à une certaine charge. Aux États-Unis, le National Institute of Science and Technology (NIST) calibre pesons place à kN 5 millions à l’aide de poids morts et mécanismes à levier. Toutes les cellules de pesage utilisés aux États-Unis doivent être traçables à cette source de calibration. Dans la pratique, des moyens de traçabilité qui se chargent de cellule A sont calibré par le NIST en utilisant des poids morts, prises aux autres laboratoires et installé en série avec peson B. Enfin, la cellule de pesage B est calibrée basée sur la comparaison de sa sortie à la sortie de la cellule de pesage A. Toutes les cellules de charge doivent être étalonnés périodiquement pour s’assurer qu’ils fonctionnent correctement.

En règle générale, la cellule de charge est installée sur une machine d’essai universelle (UTM). Un UTM comprend un châssis autonome faisant réagir avec deux colonnes de vis qui sont activées par un moteur (Fig. 4). En serrage une éprouvette dans les poignées de l’UTM et en tournant la colonne vis tels que le curseur se déplace vers le haut, les forces de traction sont introduits dans le spécimen. La force appliquée est mesurée par le capteur, qui est installé en série avec l’échantillon. En revanche, si les arbres sont installés au lieu de poignées de traction et les colonnes de vis sont déplacés vers le bas, les forces de compression sont introduits dans l’éprouvette (c.-à-d., pour tester des cylindres en béton).

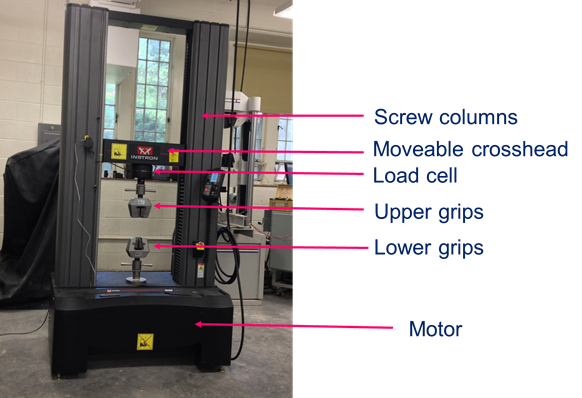
Figure 4 : Machine d’essai universelle.

Maintenant qu’il a été démontré comment mesurer la force et la souche, on discutera un traitement plus général de la théorie de l’élasticité. En regardant une pièce générique d’une structure soumis à des charges, on peut écrire les équations d’équilibre des forces et des moments sur tous les axes.

Cela se traduit par une série d’équations pour la normale (ε) et déformations de cisaillement (γ) du formulaire :

(EQ. 5)

(Équation 6)

Six équations de ce type, de trois souches normales (ε_x,_y de la εet ε_z) et de trois pour les souches de cisaillement (γ_xy, γ_yz et γ_zx) sont nécessaires pour établir les déformations globales. Ces équations contiennent trois constantes matérielles : le module d’élasticité (E), coefficient de Poisson (ν) et le module de cisaillement (G). Comme le montre l’équation ci-dessus, le module de cisaillement est la variation de la déformation angulaire donnée une contrainte de cisaillement ou de la surface de traction. Coefficient de poisson est défini comme :

(Équation 7)

Il peut être démontré que :

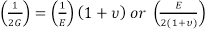= G (EQ. 8)

Ainsi, seulement deux des trois constantes nécessaire de déterminer afin de définir tous les trois. Il existe de nombreux autres constantes dérivées qui sont utilisés dans la théorie de l’élasticité, qui peuvent être tirés de ces mesures. Par exemple, le module volumique (B), ou la variation relative de volume d’un corps produit par une contrainte de traction ou de compression unitaire agissant uniformément sur toute sa surface, est :

Des égaliseurs. (5) et (6), on peut déterminer l’état de contrainte et de déformation sur une surface si au moins trois mesures de contraintes indépendantes sont effectuées. Si un extensomètre de rosette, qui a trois mesureurs à 45° vers un de l’autre (Fig. 3) est utilisé au lieu d’une seule gage longitudinale, alors on peut trouver les déformations principales minimales et maximales (ε₁, ε₂) et l’angle (Φ) entre les souches mesurées et les déformations principales du cercle de Mohr.

Pour une gage de souche rectangulaire rosette, telle que celle illustrée à la Fig. 3 où les gabarits sont à 45 degrés par rapport à l’autre :

(EQ. 9)

Φ =

La gamme de souches au cours de laquelle les relations linéaires élastiques tenir est comprise entre zéro et la limite proportionnelle du matériau. Dans cette expérience, qui utilisera l’aluminium, la gamme des souches resteront bien au-dessous de cette limite.

Nous utiliserons une poutre en porte-à-faux simple instrumentée avec des jauges de contrainte pour aider à illustrer les notions de contraintes et de déformation principale et le calcul du module de Young (E) et coefficient de Poisson (ν).  La poutre encastrée est chargée progressivement avec un ensemble de poids et les modifications correspondantes dans la souche enregistré.  Les contraintes correspondantes peuvent être calculées à partir de l’équation de contrainte flexion simple :

(EQ. 11)

où M est le moment (ou force multiplié par son bras de levier), c est la distance entre le centre de gravité et la fibre extrême du faisceau à travers sa profondeur (), et I est le moment d’inertie, donnée par où b est la largeur du faisceau et t est son épaisseur.

Module d’élasticité et coefficient de Poisson du rapport

On supposera ici que les élèves ont été formés dans les précautions d’utilisation et la sécurité nécessaires pour faire fonctionner la machine d’essai universelle.

1. Obtenir un aluminium rectangulaire bar (12 po x 1 po x ¼ po.) ; un aluminium 6061 T6xxx ou plus est recommandé. Un trou doit être percé environ 1 po de fin d’une poutre pour servir de point de chargement.
2. Marquer un emplacement sur le faisceau environ 8,0 po du centre du trou sur la surface supérieure de la poutre. Tracer des repères pour les jauges de rosette et s’assurer que les axes de la rosette sont enclins à un petit angle (environ 10° à 15°) à l’axe longitudinal de la poutre.
3. Marquer un endroit similaire sur la surface inférieure de la poutre. Un extensomètre unique sera installé ici et devrait être aligné avec l’axe longitudinal de la poutre.
4. Mesurer la largeur (b) et épaisseur (t) de la barre avec soin à l’aide d’étriers. Effectuer trois répétitions à trois endroits différents pour obtenir une bonne moyenne des dimensions. Ces mesures, de calculer le moment d’inertie (I) et la distance de l’axe neutre à la fibre extrême du bar (c = t/2).
5. Obtenir un extensomètre rosette avec une grille de détection d’environ ¼ po de long par 1/8 mm de largeur sur chaque gage et une seule souche similaire gage. Noter les facteurs d’étalonnage (ou facteur de gage) pour tous les gabarits.
6. Pour installer l’extensomètre rosette, tout d’abord dégraisser et nettoyer la surface avec soin ; poncer la surface à l’aide de papier abrasif progressivement plus fin jusqu'à l’obtention d’une surface très lisse ; nettoyer la surface avec un neutralisant ; puis collez l’extensomètre selon les spécifications du fabricant. Lorsque la colle soigner correctement avant de continuer.
7. Tester la résistance des jauges (typiquement 120 ohms) et de leur fuite de courant à la barre (résistivité, idéalement supérieure à 5 Mohms) avant de procéder.
8. Répétez les étapes 1,5 à 1,7 pour le seul gage doit être installé sur la surface inférieure.
9. Introduire l’échantillon dans l’appareil en porte-à-faux et sécuriser convenablement.
10. Connecter les jauges de contrainte à un appareil d’enregistrement, comme un indicateur de souche Vishay P3. Assurez-vous que le câblage est correct, conformément aux instructions d’indicateur de souche et que vous savez quel canal correspond à chaque extensomètre.
11. Entrez les facteurs appropriés de gage pour chaque gage dans l’indicateur.
12. Vérifier le calibrage de l’appareil en introduisant une tension connue qui se traduira par une lecture de 5000με à un facteur de gage de 2.00.
13. Chargement initial record et des souches.
14. Appliquer lentement 9 par incréments de 1 .1lbs (0,5 kg) ou similaire à la fin de la poutre. Pause à chaque étape et permettre des mesures stabiliser avant d’enregistrer des lectures.
15. Appliquer lentement 9 décrémente de 1 .1lbs (0,5 kg) ou similaire. Pause à chaque étape et permettre des mesures stabiliser avant d’enregistrer des lectures.
16. Débranchez extensomètre indicateur de souche et désactiver l’indicateur.
17. Tracer la souche dans le gage longitudinal vs la souche dans le gage transversal. La pente de cette droite correspond au coefficient de Poisson, v.
18. Déterminer la pente de la ligne meilleure ajustement de l’intrigue de stress par rapport à la déformation longitudinale, qui est égale au module de Young, E.
19. Comparer vos valeurs de E et v avec les valeurs précédemment établis ou publiés (en général, il y aura une gamme des valeurs de données plutôt qu’une seule valeur discrète).

Les données doivent être importées ou transcrit dans un tableur pour une manipulation facile et la représentation graphique. Les données recueillies sont indiquées dans le tableau 1.

Parce que l’extensomètre rosette n’est pas alignée sur les axes principaux de la poutre, les souches de rosette doivent être entrés dans les équations pour ε_{1, 2} (EQ. 9) et ε (équation 10) ci-dessus pour calculer les déformations principales, ayant pour résultat les chiffres indiqués dans le tableau 2. Le tableau montre que l’angle entre le stress mesuré et les contraintes principales à 0,239 13,7 ° degrés ou radians. Notez que la souche principale maximale est positive, correspondant à une forte contrainte de traction longitudinale ; la déformation principale minimale est négative, correspondant à une plus petite souche compression transversale. Le rapport entre les déformations principales minimales et maximales correspond au coefficient de Poisson, ce qui est indiqué sur la dernière colonne et en moyenne sur 0,310.

	Charge	Gage 1	Gage 2	Gage 3	44 de gage
Étape	(Lb.)	ΜΕ	ΜΕ	ΜΕ	ΜΕ
1	0.00	1	1	1	0
2	1.10	83	56	-21	-87
3	2.21	163	115	-41	-171
4	3.31	243	171	-62	-254
5	4.42	325	228	-83	-338
6	5.52	400	280	-104	-423
7	6.62	485	338	-122	-501
8	7.73	557	386	-143	-589
9	8.83	634	442	-163	-665
10	9.93	714	502	-184	-741
11	8.83	637	445	-162	-664
12	7.73	561	391	-142	-584
13	6.62	483	335	-123	-506
14	5.52	406	281	-102	-423
15	4.42	323	227	-83	-339
16	3.31	245	171	-62	-256
17	2.21	164	115	-41	-170
18	1.10	83	56	-21	-87
19	0.00	1	0	1	2

Tableau 1 : Les souches dans la barre d’aluminium.

Facteur de gage	1	2	3	Déformation maximale Principal	Minimum. Souche principale	Angle	Coefficient de poisson
Échelon de charge	ΜΕ	ΜΕ	ΜΕ	(EQ. 9)	(EQ. 9)	(Équation 10)	(Équation 7)
1	1	1	1	1	1	0	0
2	83	56	-21	89	-26	-0.223	0,297
3	163	115	-41	176	-55	-0.243	0.311
4	243	171	-62	263	-82	-0.242	0,312
5	325	228	-83	351	-109	-0.240	0.311
6	400	280	-104	432	-136	-0.240	0,314
7	485	338	-122	523	-160	-0.237	0,307
8	557	386	-143	600	-186	-0.236	0,310
9	634	442	-163	684	-213	-0.238	0,312
10	714	502	-184	773	-242	-0.242	0,314
11	637	445	-162	688	-213	-0.239	0,309
12	561	391	-142	605	-186	-0.237	0,308
13	483	335	-123	520	-161	-0.236	0,309
14	406	281	-102	437	-133	-0.234	0,303
15	323	227	-83	349	-109	-0.241	0,313
16	245	171	-62	264	-81	-0.238	0,308
17	164	115	-41	177	-54	-0.239	0,302
18	83	56	-21	89	-26	-0.223	0,297
19	1	0	1	2	0	0,000	0,000
					Moyenne	-0.239	0,310

Tableau 2 : Principales souches et angle d’inclinaison.

Les déformations principales minimales et maximales du tableau 2 sont tracées sur la Fig. 5, qui montre des tendances très linéaires (R² = 0,999) pour le coefficient de Poisson. La valeur obtenue pour le coefficient de Poisson (0,31), qui correspond à la pente de la droite, est très proche du 0.30 donnée dans la plupart des références pour l’aluminium et autres métaux.

Figure 5 : Principal souche données montrant la pente de la ligne entre la déformation principale minimale et maximale, qui correspond au coefficient de Poisson.

Une bonne interprétation physique des données rosette strain gage peut être obtenue de tracer les déformations principales sur un cercle de Mohr (Fig. 6). Remarque que les trois mesures, montrées ici dans le cas de la charge maximale de 7,4 lb, correspondent à trois points dans le cercle à 90 ° les uns des autres, en commençant à un angle d’environ 27.4º (ou 2Φ) vers la gauche de l’axe des abscisses.

Figure 6 : Signification physique des lectures de rosette de souche montré sur le cercle de Mohr pour souche.

Le tableau 3 montre les charges, les résultats de la déformation en traction principale de la gage unique sur la face inférieure de la poutre (Gage 4, qui est en compression), le ratio entre le fond et les contraintes principales maximales supérieurs, le stress de l’équation (11) et de Young module (E) comme le rapport de l’effort de l’équation (11) la déformation de l’équation (9). Dans le tableau 3, un module d’Young est calculé comme 10147 ksi en calculant la moyenne des modules calculés pour les 15 étapes de chargement intermédiaire.

	Charge	Max. Principal. Souche	Max principaux Stress	Min Principal Stress	Contrainte de flexion	Young' module
Échelon de charge	Lbs.	ΜΕ	ksi	ksi	lb/po2	ksi
1	0.00	1	10	9	0	0
2	1.10	89	886	0	882	9945
3	2.21	176	1765	0	1763	9991
4	3.31	263	2630	0	2645	10058
5	4.42	351	3513	0	3526	10038
6	5.52	432	4324	0	4408	10195
7	6.62	523	5230	0	5290	10113
8	7.73	600	6001	0	6171	10283
9	8.83	684	6843	0	7053	10307
10	9.93	773	7726	0	7935	10269
11	8.83	688	6877	0	7053	10256
12	7.73	605	6051	0	6171	10198
13	6.62	520	5204	0	5290	10165
14	5.52	437	4368	0	4408	10091
15	4.42	349	3494	0	3526	10092
16	3.31	264	2644	0	2645	10004
17	2.21	177	1770	0	1763	9960
18	1.10	89	886	0	882	9945
19	0.00	2	19	0	0	0
					Moyenne	10147

Tableau 3 : Calcul du module d’élasticité (E).

Les données pour E sont également tracées sur la Fig. 7, ce qui indique une excellente relation linéaire (haute R²) entre le stress et la fatigue et une pente d’environ 10 147 ksi. La différence entre le module du tableau 3 et celui de la Fig. 6 surgit parce que les calculs pour la pente à la Fig. 6 exigent que l’interception passent par zéro. Les amplitudes comparent très avantageusement (erreur inférieure à 1,5 %) avec les valeurs de E del ' aluminium 6061 t 6, qui est généralement donnée comme 10 000 ksi.

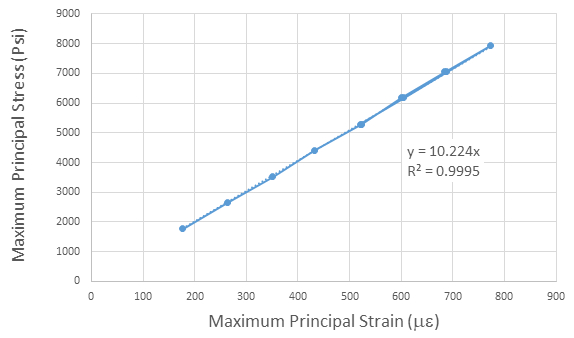
Figure 7 : Pente de la ligne de contrainte maximale contre la déformation maximale est le module d’Young.

Enfin, par la refonte des égaliseurs. (5) et (6) en :

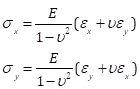(Équation 12)

Nous pouvons calculer les contraintes principales à l’aide du cercle de Mohr. Dans le cas de l’échelon correspondant à 6,61 lb de charge, les principales souches (634,-189) entraînent des contraintes principales de (7.34, 0.00) ksi (Fig. 8). Bien qu’ici, les calculs sont effectués en utilisant les expressions pour contraintes planes, les résultats correctement indiquent que le long de l’axe principal, la contrainte dans la direction perpendiculaire est zéro (ou très près de lui), ce qui correspond au cas d’uniaxiale. Les valeurs de contrainte à un angle de 2Φ = 0,40 radians sont (6.50, 2,82) ksi.

Figure 8 : Cercle de Mohr des contraintes planes dans le cas d’une charge de 7,34 lbs.

Dans cette expérience, on a mesuré les deux constantes de matières fondamentales : le module d’élasticité (E) et coefficient de Poisson (v). Cette expérience montre comment mesurer ces constantes dans un laboratoire à l’aide d’un extensomètre de rosette. Les valeurs obtenues expérimentalement correspondent bien avec les valeurs publiées de 10 000 ksi et 0,3, respectivement. Ces valeurs sont essentiels dans l’application de la théorie de l’élasticité pour la conception technique, et cette technique expérimentale décrite dans les présentes sont typiques de ceux utilisés pour l’obtention des constantes de matériaux. Pour obtenir ces valeurs, grand il faut tous les deux utilisant l’instrumentation de haute résolution et des procédures d’étalonnage traçable. En particulier, l’utilisation de la souche gage des équipements et systèmes d’acquisition de données numériques 16 à 24 bits font partie intégrante de la réussite et la qualité de ces expériences.

Aujourd'hui, il y a des autres méthodes de détermination d’Young d’un matériau, y compris les méthodes de propagation des ondes (méthode de l’écho-impulsion ultrasonique) et nanoindentation. Un des avantages de l’utilisation de propagation des ondes, c’est que c’est une des méthodes non destructives de mesurage d’Young, tandis que nanoindentation et l’utilisation d’un extensomètre rosette sont des méthodes plus invasives.

La conception de tout produit d’ingénierie, d’un grille-pain à un gratte-ciel, nécessite l’utilisation de modèles analytiques efficaces pour améliorer et optimiser la conception. La théorie de l’élasticité est le fondement de la plupart des modèles utilisés dans la conception du génie civil et repose sur la mise en place de plusieurs constantes.

Modèles analytiques sont requises pour seulement une réplique simple (ou très peu) sera construit. Comme le coût et le rendement de la structure dépendant du résultat de ces analyses et ces analyses, dépendent à leur tour, ayant de solides valeurs pour les propriétés des matériaux, essais tels que ceux décrits ici doivent être exécutés pour assurer la qualité et contrôle de la qualité assurance en cours de construction. Par exemple :

• En choisissant une façade d’un bâtiment, l’architecte doit être prudent concevoir une enveloppe imperméable à l’eau. L’étanchéité à l’eau d’un bâtiment de façade en briques peut dépendre de maintenir le mortier entre les briques résiduel, entre autres facteurs. Si le mortier fend, eau pénétrer et provoquer de la corrosion et les problèmes d’humidité qui seront très coûteux à corriger. Afin de déterminer quelle force le mortier peut résister avant il craque, il faut une théorie et ses constantes associées. L’ingénieur architecte et structurelles doit travailler ensemble pour déterminer ce qui charge la volonté de façade voir (poids propre, vent, conduisant à la pluie, etc.) et comment chaque option design se produira dans ces conditions. Alors seulement peut un mortier avec des caractéristiques appropriées doivent être choisi.
• Dans la construction d’un grand bâtiment, tels que la tour Burj Dubaï, la compagnie de construction a besoin d’être très attentif à maintenir le niveau des planchers. En cours de construction, si les tailles des colonnes et des murs sont différents, certains de ces éléments peuvent raccourcir (souche) plus que d’autres en cours de construction et plus de poids (stress) est ajouté. Pour obtenir un plancher plat à la fin de la construction, l’entreprise de construction devra faire des ajustements à la hauteur des colonnes et des murs dans les étages inférieurs - les étages inférieurs peuvent ne pas être de niveau durant les phases initiales de construction mais devraient être plat à la fin. Pour calculer comment faire correctement ces ajustements, la société de construction embauchera un ingénieur en structure de fournir des données sur la colonne différentiel et des hauteurs de mur. L’ingénieur devront utiliser des constantes matérielles pour effectuer ces calculs.
• Dans la conception d’une canette de soda, un fabricant doit réduire au minimum l’épaisseur de la paroi en aluminium, comme l’aluminium est un matériau très coûteux. Afin d’optimiser la forme et les dimensions des bidons, le fabricant doit déterminer quelles conditions de chargement sont importantes ; conditions de transport et de stockage peuvent être plus exigeant que le consommateur buvant à elle. Beaucoup de ces conditions sera difficile et coûteuse à reproduire dans un programme expérimental d’essais ; le constructeur peut choisir de faire beaucoup d’analyse afin d’optimiser les dimensions de la boîte avant de passer à la phase de prototype. Cette procédure est ce que Boeing a inspiré l’élaboration du Dreamliner (Boeing 787). Pour faire ces études, propriétés des matériaux doivent être connues et la théorie appropriée sélectionné.