材料常数

用于分析的最常见的模型是线性弹性 (胡克定律), 它假定力的变化 (F) 与尺寸 (Δ) 的变化成正比。在单轴载荷情况下最简单的形式, 力和变形是由一个常数 (E) 或弹性模量来关联的:

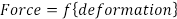(Eq 1)

(Eq 2)

(Eq 3)

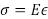(Eq 4)

正如上面的等式所描述的, 应力和应变是工程量, 而不是实际数量。真正的数量需要一个来测量局部尺寸的微小但有限的变化, 随着力的增加而发生。实验上, 即使在非接触测量技术的最新进展下, 这一壮举也很难完成。对于这些计算, 你可以假设这些变化是微不足道的, 并使用原来的面积 (₀) 和长度 (L₀)。

为了从上述方程中确定弹性模量, 必须有一种方法来确定试样加载时的力和长度的变化。在一个粗略的实验中, 人们可以使用卫生间秤和尺子来完成这些任务。首先, 你可以采取一个厚的橡皮筋, 测量其尺寸, 并标记两个点在带分开一英寸。接下来, 你可以放置一个开放的容器在一个规模, 并添加水, 直到读数是十英镑。然后, 你可以用橡皮筋将容器挂起, 并测量两个标记之间的分离程度。这项测量将给我们所有的数据, 以计算的橡胶 e, 因为我们有所有的价值, 以解决 e 在情商。(2) 通过 (4)。然而, 由于非常粗糙的测量装置, 测量结果会产生很大的不确定性和误差。由于典型建筑材料所需的应变量是按 1x10^-6的顺序计算的, 因此在实验中确定材料常数需要更精确的测量装置。对于大多数常见的工程应用, 这些测量是基于电阻应变计。由于这些设备将在整个后续视频中使用, 接下来将给出他们的操作原则的描述。

应变计是嵌入在载波矩阵上的长环形线 (图 2)。应变片粘附在用高强度环氧树脂测试的材料上。当材料变形时, 导线的长度会发生变化, 因此电阻会稍有变化。当测量器作为惠斯通电电桥电路的一部分插入时, 这些变化可以被检测为电压的变化。数字测量系统的出现大大减少了电路中的背景噪声和其他误差源, 从而提高了今天测量电压变化的精确度。应变片是用一个常数称为测量因子来校准的, 因此它的输出与给定的电压输入下给定应变范围的应变线性相关。

应变计只测量一个方向的应变。为了获得在表面上的一个点上的完整的应力状态, 需要一个玫瑰应变片, 由三应变计组成的45º对彼此是必要的 (图 3)。在三个不同方向的测量中, 表面应力的整个状态可以用摩尔的圆来计算最大和最小的主应变和应力来定义。

图 2: 应变计.

图 3: 玫瑰花应变计.

力的测量也用应变计进行;然而, 这些测量通常是在一个完整的桥配置 (即, 在惠斯通电桥电路内部电阻被外部有源测量器取代) 导致一个设备称为负载单元。负载单元本身通常是一个厚, 高强度的钢缸, 两个量具纵向安装和两个横向安装, 以消除泊松比的影响。负载单元的校准要求使用死重, 以便电路的电压输出可以与给定负载相关。在美国, 国家科学技术研究院 (NIST) 校准的负载细胞多达 500万 kN, 使用的是死重量和杠杆机制。所有在美国使用的负载单元必须可追溯到这个校准源。在实际操作中, 可追溯性意味着由 NIST 使用死重量校准负载单元 A, 并将其带到其他实验室, 并安装在带有负载单元 B 的系列中。最后, 对负载单元 B 进行了标定, 并将其输出与负载单元 A 的输出进行了比较。必须定期校准所有的负载单元格, 以确保它们正常工作。

通常, 负载单元格安装在通用测试机 (UTM) 上。一个 UTM 由一个自反应框架组成, 两个螺柱由马达转动 (图 4)。通过将测试标本夹入到该夹具中, 并转动螺钉柱, 使十字头向上移动, 将拉伸力引入试样中。所施加的力由荷载单元测量, 并与试样串联安装。另一方面, 如果安装了压台而不是拉紧手柄, 而螺钉柱向下移动, 则将压缩力引入试验试样 (即测试混凝土钢瓶)。

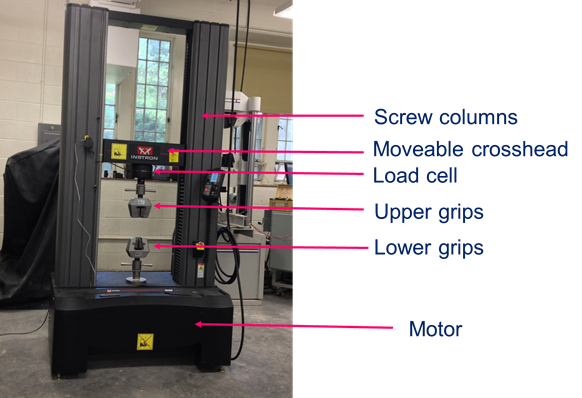
图 4: 万能试验机.

现在已经证明了如何测量应变和力, 对弹性理论的更一般的处理将被讨论。看着一个结构的一般片断受荷载, 你可以写平衡方程的力量和时刻沿所有轴。

这就形成了一系列等式 (ε) 和剪切 (γ) 应变的形式:

(Eq 5)

(Eq 6)

六个这种类型的等式, 三为正常菌株(ε_x, ε_y和ε_z) 和三为剪切菌株 (γ_xy, γ_yz和γ₎ , 需要建立全局变形。这些方程包含三物质常数: 弹性模量 (E)、泊松比 (ν) 和剪切模量 (G)。如上图所示, 剪切模量是由于剪切应力或表面牵引力而引起的角形变变化。泊松比定义为:

(Eq 7)

可以看出:

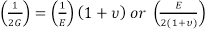= G (Eq 8)

因此, 为了定义所有三, 仅需要确定三个常量中的两个。在弹性理论中还有许多其他的派生常数, 所有这些常量都可以从这些测量中获得。例如, 体积模数 (B), 或在其表面上均匀作用的单位压缩或拉伸应力所产生的物体体积的相对变化是:

从情商。(5) 和 (6), 如果至少有三个独立的应变测量, 就可以确定表面的应力和应变状态。如果一个玫瑰应变计, 其中有三个量规在45°彼此 (图 3), 而不是一个单一的纵向测量, 然后你可以找到最大和最小的主要菌株 (ε₁, ε₂) 和角度 (Φ) 之间的测量菌株和摩尔的圆圈的主要菌株。

对于一个长方形的玫瑰应变计, 如图3所示的, 其中的量规是在45度, 以彼此:

(Eq 9)

Φ =

线性弹性关系所保持的应变范围介于零和材料的比例极限之间。在这个将使用铝的实验中, 菌株的范围将保持在这个极限之下。

我们将使用一个简单的悬臂梁的应变计, 以帮助说明主应变和应力的概念, 并计算杨氏模量 (E) 和泊松比 (ν)。 悬臂梁将以一组权重增量加载, 并记录应变的相应变化。 相应的应力可以从简单的弯曲应力方程计算出来:

(Eq 11)

当 M 是片刻 (或力量乘以它的杠杆胳膊), c 是距离从质心到极端纤维在横梁横跨它的深度 (), 并且我是惯性的时刻, 给由 b 是光束宽度和 t 是它的厚度。

数据应该导入或转录到电子表格中, 以便于操作和绘图。所收集的数据见表1。

由于莲座丛应变片不与梁的主轴相对准, 因此需要将莲座丛菌株输入到₁₂ (eq 9) 和上面的ε (eq 10) 的方程中, 以计算主应变, 从而产生表2中显示的数据。结果表明, 实测应力与主应力的夹角约为0.239 弧度或13.7°。注意最大主应变为正, 纵向对应大拉伸应变;最小主应变为负, 对应于较小的横向压缩应变。最小和最大主应变的比值对应于泊松比, 这在最后一列显示, 平均值约为0.310。

	负荷	量具1	量具2	量具3	量具44
步	(磅)	με	με	με	με
1	0.00	1	1	1	0
2	1.10	83	56	-21	-87
3	2.21	163	115	-41	-171
4	3.31	243	171	-62	-254
5	4.42	325	228	-83	-338
6	5.52	400	280	-104	-423
7	6.62	485	338	-122	-501
8	7.73	557	386	-143	-589
9	8.83	634	442	-163	-665
10	9.93	714	502	-184	-741
11	8.83	637	445	-162	-664
12	7.73	561	391	-142	-584
13	6.62	483	335	-123	-506
14	5.52	406	281	-102	-423
15	4.42	323	227	-83	-339
16	3.31	245	171	-62	-256
17	2.21	164	115	-41	-170
18	1.10	83	56	-21	-87
19	0.00	1	0	1	2

表 1: 铝棒中的应变。

量具系数	1	2	3	最大主应变	最低。主应变	角度	泊松比
加载步骤	με	με	με	(Eq 9)	(Eq 9)	(Eq 10)	(Eq 7)
1	1	1	1	1	1	0	0
2	83	56	-21	89	-26	-0.223	0.297
3	163	115	-41	176	-55	-0.243	0.311
4	243	171	-62	263	-82	-0.242	0.312
5	325	228	-83	351	-109	-0.240	0.311
6	400	280	-104	432	-136	-0.240	0.314
7	485	338	-122	523	-160	-0.237	0.307
8	557	386	-143	600	-186	-0.236	0.310
9	634	442	-163	684	-213	-0.238	0.312
10	714	502	-184	773	-242	-0.242	0.314
11	637	445	-162	688	-213	-0.239	0.309
12	561	391	-142	605	-186	-0.237	0.308
13	483	335	-123	520	-161	-0.236	0.309
14	406	281	-102	437	-133	-0.234	0.303
15	323	227	-83	349	-109	-0.241	0.313
16	245	171	-62	264	-81	-0.238	0.308
17	164	115	-41	177	-54	-0.239	0.302
18	83	56	-21	89	-26	-0.223	0.297
19	1	0	1	2	0	0.000	0.000
					平均	-0.239	0.310

表 2: 主要菌株和倾角。

表2中的最大和最小主要菌株绘制在图5中, 它显示了泊松比的线性趋势 (R² = 0.999)。所获得的泊松比 (0.31), 它对应于直线的斜率, 是非常接近0.30 所给出的大多数参考铝和其他金属。

图 5: 主应变数据显示最大和最小主应变线之间的斜率, 对应于泊松比.

通过绘制莫尔圆上的主要菌株 (图 6), 可以获得对玫瑰花应变片数据的良好物理解释。请注意, 三测量, 这里显示的情况下, 最大负荷7.4 磅, 对应到三点在90º之间的圆圈, 从一个角度约 27.4º (或2Φ) 逆时针从 x 轴。

图 6: 在摩尔的应变圆上显示的应变花环读数的物理意义.

表3显示了负载, 计算结果为主拉伸应变从梁底面上的单片 (压力计 4), 底部和最高最大主应力的比值, 从 Eq 的应力. (11), 杨氏模量 (E) 作为压力与 eq 的比值 (11) 除以 eq 的应变. (9)。在表3中, 将杨氏模量计算为 10147 ksi, 方法为15中间加载步骤计算的模数平均值。

	负荷	麦克斯。主要。应变	最大主应力	最小主应力	弯曲应力	杨氏模量
加载步骤	磅。	με	ksi	ksi	Psi	ksi
1	0.00	1	10	9	0	0
2	1.10	89	886	0	882	9945
3	2.21	176	1765	0	1763	9991
4	3.31	263	2630	0	2645	10058
5	4.42	351	3513	0	3526	10038
6	5.52	432	4324	0	4408	10195
7	6.62	523	5230	0	5290	10113
8	7.73	600	6001	0	6171	10283
9	8.83	684	6843	0	7053	10307
10	9.93	773	7726	0	7935	10269
11	8.83	688	6877	0	7053	10256
12	7.73	605	6051	0	6171	10198
13	6.62	520	5204	0	5290	10165
14	5.52	437	4368	0	4408	10091
15	4.42	349	3494	0	3526	10092
16	3.31	264	2644	0	2645	10004
17	2.21	177	1770	0	1763	9960
18	1.10	89	886	0	882	9945
19	0.00	2	19	0	0	0
					平均	10147

表 3: 弹性弹性模量的计算 (E)。

E 的数据也绘制在图7中, 它表示应力和应变之间的良好线性关系 (高 R²) 和一个大约 10147 ksi 的斜率。表3和图6中的模量之间的差异之所以出现, 是因为图6中的斜率计算要求拦截通过零。震级比较有利 (错误少于 1.5%) 与出版的价值 E 为6061T6 铝, 通常被给作为 1万 ksi。

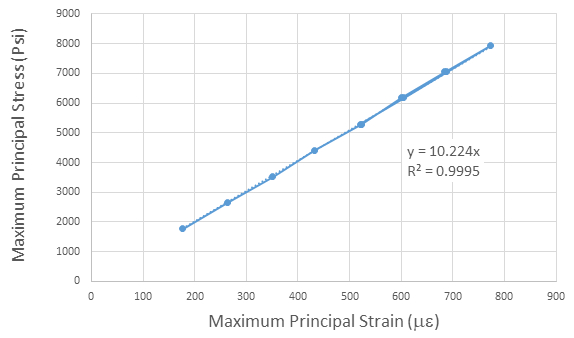
图 7: 最大应力线斜率与最大应变为杨氏模量.

最后, 通过重铸情商。(5) 和 (6) 进入:

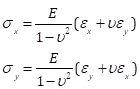(Eq 12)

我们可以用摩尔的圆来计算主应力。对于对应于6.61 磅负载的步骤, 主应变 (634、-189) 导致主应力 (7.34、0.00) ksi (图 8)。虽然这里的计算是用平面应力的表达式完成的, 但结果正确地表明沿主轴的垂直方向上的应力是零 (或非常接近), 对应于单轴加载的情况。重音值在2Φ的角度 = 0.40 弧度是 (6.50, 2.82) ksi。

图 8: 摩尔的圆为平面应力的情况下, 7.34 磅负荷.

在本实验中, 测量了两个基本材料常数: 弹性模量 (E) 和泊松比 (v)。本实验演示了如何使用玫瑰应变计测量实验室设置中的这些常数。实验所得的值分别与 1万 ksi 和0.3 的公布值吻合较好。这些值是应用弹性理论进行工程设计的关键, 本文所描述的实验技术是获取材料常数的典型方法。要获得这些值, 必须非常小心地使用高分辨率仪器和可追踪的校准程序。特别是, 使用基于应变仪的设备和16到24位数字数据采集系统是这类实验的成功和质量的组成部分。

今天, 还有其他方法来确定材料的杨氏模量, 包括波传播方法 (超声波回波脉冲法) 和纳米压痕。利用波传播的一个好处是, 它是测量杨氏模量的非破坏性方法之一, 而压痕和玫瑰花应变片的使用则是更具侵入性的方法。

任何工程产品的设计, 从烤箱到摩天大楼, 都需要使用有效的分析模型来改进和优化设计。弹性理论是土木工程设计中应用最多的模型的基础, 是建立几个常数的基础。

如果只生成单个 (或很少) 复制, 则需要分析模型。由于结构的成本和性能取决于这些分析的结果, 而这些分析反过来又依赖于具有可靠的材料性能值, 因此必须运行此处描述的测试, 以确保质量控制和质量施工过程中的保证。例如:

• 在为建筑物选择门面时, 建筑师必须小心设计防水信封。砖砌体立面的水密性可能取决于在砖无裂纹之间保持砂浆, 以及其他因素。如果砂浆开裂, 水就会穿透, 造成腐蚀和湿度的问题, 这将是非常昂贵的修复。为了确定砂浆在裂纹前能抵抗多少力, 我们需要一个理论及其相关常数。建筑师和结构工程师必须共同努力, 确定门面将看到什么 (自重, 风, 驾驶雨等), 以及每个设计选项将如何在这些条件下执行。只有这样, 才能选择具有适当特征的砂浆。
• 在建造一座高楼, 如迪拜塔, 建筑公司需要密切注意保持楼层水平。随着施工的进展, 如果柱和墙的尺寸不同, 这些元素中的一些可能会比其他的更短 (应变), 随着施工的进展和更多的重量 (应力) 增加。为了在施工结束时获得平坦的楼层, 建筑公司将需要对底层的柱子和墙的高度进行调整--底层在施工初期可能不是水平的, 但应该是平底的。为了计算如何正确地进行这些调整, 建筑公司将聘请一个结构工程师, 提供差异柱和墙高的数据。工程师将需要使用材料常数来进行这些计算。
• 在汽水罐的设计中, 制造商必须尽量减少铝壁的厚度, 因为铝是一种非常昂贵的材料。为了优化罐的形状和尺寸, 制造商需要确定哪些装货条件是重要的;运输和贮存条件可能比饮用它的消费者要求更高。在实验测试程序中, 许多这些条件将很难和昂贵的复制;制造商可以选择做大量的分析, 以优化的能力尺寸, 然后再移动到原型阶段。这一程序是波音公司在开发梦幻飞机 (波音 787) 之后所遵循的。要做这些研究, 材料属性必须是已知的和适当的理论选择。