재료 상수

분석에 사용되는 가장 일반적인 모델은 선형 탄성(Hooke's Law)으로, 힘(F)의 변화가 차원(Δ)의 변화에 직접적으로 비례한다고 추정합니다. 동축 적재의 경우 가장 간단한 형태로 힘과 변형은 단일 상수 (E) 또는 탄성의 계수에 의해 관련됩니다.

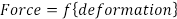(Eq. 1)

(Eq. 2)

(Eq. 3)

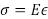(Eq. 4)

위의 방정식에 설명된 바와 같이, 응력과 변형은 실제 수량과 는 달리 엔지니어링 수량입니다. 실제 수량은 힘이 증가함에 따라 발생하는 로컬 차원의 작지만 유한한 변화를 측정해야 합니다. 이러한 위업은 최근 비접촉 측정 기술의 발전에도 불구하고 달성하기가 매우 어렵습니다. 이러한 계산의 경우 이러한 변경 내용을 무시할 수 있다고 가정하고 원래 영역(A₀₎및 길이(L_0)를사용할 수 있습니다.

위의 방정식으로부터 탄성의 계수를 결정하기 위해서는 시편이 로드됨에 따라 힘및 길이의 변화를 결정하는 방법이 있어야 한다. 조잡한 실험에서, 하나는 이러한 작업을 수행하기 위해 욕실 규모와 통치자를 사용할 수 있습니다. 첫째, 두꺼운 고무 밴드를 가지고 크기를 측정하고 1 인치로 분리 된 밴드에 두 점을 표시 할 수 있습니다. 다음으로, 하나는 규모에 열린 용기를 배치하고 독서가 10 파운드 가 될 때까지 물을 추가 할 수 있습니다. 그런 다음 고무 밴드로 컨테이너를 일시 중단하고 두 마크가 분리된 양을 측정할 수 있습니다. 이 측정은 Eqs에서 E를 해결하는 데 필요한 모든 값을 가지고 있기 때문에 고무에 대해 E를 계산하는 데 필요한 모든 데이터를 제공합니다. (2) 통해 (4). 그러나 매우 조잡한 측정 장치로 인해 측정과 관련된 매우 큰 불확실성과 오류가 있을 것입니다. 일반적인 건축 자재에 대해 측정해야 하는 균의 크기는^1x10-6의순서에 있기 때문에, 실험적으로 재료 상수를 결정하기 위해 훨씬 더 정확한 측정 장치가 필요합니다. 대부분의 일반적인 엔지니어링 응용 분야에서 이러한 측정은 전기 저항 변형 게이지를 기반으로 합니다. 이러한 장치는 후속 동영상에서 사용되기 때문에 운영 원칙에 대한 설명이 다음에 제공됩니다.

스트레인 게이지는 캐리어 매트릭스에 내장된 긴 루프 와이어(도 2)이다. 스트레인 게이지는 고강도 에폭시로 테스트되는 재료에 접착됩니다. 재료가 변형되면 와이어의 길이가 변경되고 그 저항은 결과적으로 약간 변경됩니다. 게이지가 휘트스톤 브리지 회로의 일부로 삽입되면 전압의 변화로 이러한 변화를 감지할 수 있습니다. 디지털 측정 시스템의 출현으로 회로 내의 배경 소음 및 기타 오류 소스가 상당히 감소하여 오늘날 전압 변화를 측정할 수 있는 정밀도를 향상시켰습니다. 스트레인 게이지는 게이지 계수로 알려진 상수를 사용하여 보정되므로 출력은 주어진 전압 입력하에서 지정된 변형 범위에 대한 변형과 선형적으로 관련이 있습니다.

스트레인 게이지는 한 방향으로만 변형을 측정합니다. 표면상의 한 지점에서 완전한 응력 상태를 얻기 위해서는 45º에서 서로 정렬된 3개의 스트레인 게이지로 구성된 로제트 스트레인 게이지(도 3)가 필요하다. 이러한 측정을 세 가지 방향으로 사용하면 Mohr의 원과 같은 원리를 사용하여 최대 및 최소 주균 및 응력을 계산하여 표면의 전체 스트레스 상태를 정의할 수 있습니다.

그림 2: 스트레인 게이지.

그림 3: 로제트 스트레인 게이지.

힘의 측정은 또한 변형 게이지로 이루어집니다; 그러나 이러한 측정은 일반적으로 전체 브리지 구성(즉, 휘트스톤 브리지 회로의 내부 저항이 외부 활성 게이지으로 대체됨)에서 수행되어 로드 셀이라고 하는 장치가 발생합니다. 로드 셀 자체는 일반적으로 두 개의 게이지가 세로로 설치되고 푸아송 비율의 영향을 제거하기 위해 두 개의 게이지가 횡적으로 설치된 두 개의 고강도 강철 실린더입니다. 로드 셀의 보정을 위해서는 회로의 전압 출력이 지정된 부하와 관련될 수 있도록 데드 웨이트를 사용해야 합니다. 미국에서는 국립 과학 기술 연구소(NIST)가 데드 웨이트와 레버 메커니즘을 사용하여 최대 500만 kN의 로드 셀을 교정합니다. 미국에서 사용되는 모든 로드 셀은 이 교정 소스로 추적할 수 있어야 합니다. 실제로 추적성은 로드 셀 A가 데드 웨이트를 사용하여 NIST에 의해 보정되고 다른 실험실로 이동하며 로드 셀 B와 함께 계열로 설치된다는 것을 의미합니다. 마지막으로 로드 셀 B는 출력을 로드 셀 A의 출력과 비교하여 보정됩니다. 모든 로드 셀은 제대로 작동하는지 확인하기 위해 주기적으로 보정되어야 합니다.

일반적으로 로드 셀은 범용 테스트 기계(UTM)에 설치됩니다. UTM은 모터로 회전하는 두 개의 나사 열이 있는 자체 반응 프레임으로 구성됩니다(도 4). 시험 표본을 UTM 그립으로 고정하고 크로스헤드가 위쪽으로 이동할 수 있도록 나사 컬럼을 돌리면 인장력이 시편에 도입됩니다. 적용된 힘은 시편과 연재된 로드 셀에 의해 측정됩니다. 반면에 인장 그립 대신 플라톤이 설치되고 나사 기둥이 아래로 이동하는 경우, 압축력이 시험 시편(즉, 콘크리트 실린더를 테스트하기 위해)에 도입된다.

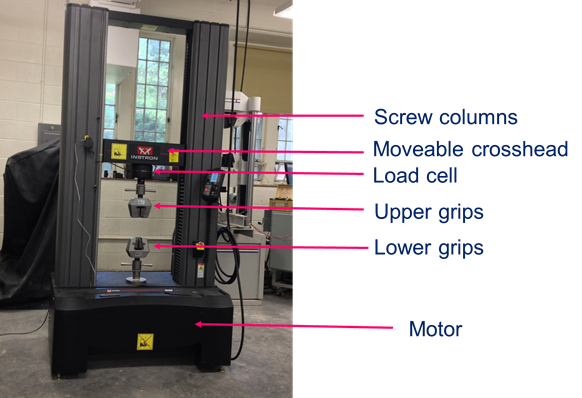
그림 4: 범용 테스트 기계.

이제 변형과 힘을 측정하는 방법을 입증되었으므로 탄성 이론에 대한 보다 일반적인 치료가 논의될 것입니다. 하중을 받는 구조의 일반적인 조각을 살펴보면 모든 축을 따라 힘과 모멘트에 대한 평형 방정식을 작성할 수 있습니다.

이렇게 하면 양식의 일반(ε)과 전단(γ) 균주에 대한 일련의 방정식이 생성됩니다.

(Eq. 5)

(Eq. 6)

이 유형의 여섯 방정식, 정상 균주에 대한 세(ε_x, ε_y 및 ε_z)및 전단 균주에 대한 세(γ_xy, γ_yz 및 γ_zx)는 글로벌 변형을 확립하는 데 필요합니다. 이러한 방정식에는 탄성(E), 푸아송의 비율(θ), 전단 계수(G)의 계수가 세 가지 재질 상수를 포함합니다. 위의 방정식에 나타난 바와 같이, 전단 변조기는 전단 응력 또는 표면 견인을 감안할 때 각 변형의 변화이다. 푸아송의 비율은 다음과 같이 정의됩니다.

(Eq. 7)

다음과 같은 것을 보여 주어질 수 있습니다.

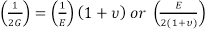= G (Eq. 8)

따라서 세 상수 중 2개만 결정하여 세 상수를 모두 정의해야 합니다. 탄성 이론에 사용되는 수많은 다른 파생 상수가 있으며, 이들 측정에서 파생될 수 있습니다. 예를 들어, 벌크 계수(B) 또는 표면에서 균일하게 작용하는 유닛 압축 또는 인장 응력에 의해 생성된 신체의 부피의 상대적 변화는 다음과 같이 다음과 같이 한다.

Eqs에서. (5) 및 (6), 적어도 3개의 독립적인 변형 측정이 이루어지면 표면에 응력 및 부담 상태를 결정할 수 있다. 45°에서 서로 3개의 게이지를 가지고 있는 로제트 스트레인 게이지(도 3)가 단일 세로 게이지 대신 사용되는 경우, 측정된 균주와 모어원의 주균 사이의 최대 및 최소 주체균(ε_1, ε_2)과각도(φ)를 찾을 수 있습니다.

직사각형 로제트 스트레인 게이지의 경우, 게이지는 서로 45도에 있는 도 3에 도시된 것과 같은:

(Eq. 9)

Φ =

선형 탄성 관계가 보유하는 균주 범위는 재료의 0과 비례 한계 사이입니다. 알루미늄을 사용하는이 실험에서 균주의 범위는 그 한계보다 훨씬 낮게 유지됩니다.

우리는 주 변형 과 스트레스의 개념과 영의 변조기 (E)와 푸아송의 비율 (θ)의 계산을 설명하는 데 도움이 변형 게이지와 계측 간단한 캔틸레버 빔을 사용합니다.  캔틸레버 빔은 가중치 집합과 그에 상응하는 변형 이기록으로 점진적으로 로드됩니다.  해당 응력은 간단한 굽힘 응력 방정식에서 계산할 수 있습니다.

(Eq. 11)

M이 모멘트(또는 레버 암에 곱한 힘)인 경우, c는 심도를 가로지르는 빔의 극한 섬유까지의 거리이며, b가 빔 폭이고 t가 두께인 곳에 주어진 관성의 순간이다.

쉽게 조작하고 그래프를 전송할 수 있는 데이터를 스프레드시트에 가져오거나 전사해야 합니다. 수집된 데이터는 표 1에 표시됩니다.

로제트 스트레인 게이지는 빔의 주축과 정렬되지 않기 때문에, 로제트 균주는 ε_1,2(Eq. 9) 및 ε(Eq. 10)에 대한 방정식에 입력하여 주균을 계산하여 표 2에 표시된 데이터를 생성한다. 표는 측정된 응력과 주응력 사이의 각도가 약 0.239 라디안 또는 13.7°임을 보여줍니다. 최대 주균은 큰 인장 균주에 세로로 대응하는 양수입니다. 최소 원주 균주는 더 작은 횡방향 압축 변형에 대응하는 음수입니다. 최소 및 최대 주체 사이의 비율은 마지막 열에 표시되고 평균 0.310에 표시되는 푸아송의 비율에 해당합니다.

	부하	게이지 1	게이지 2	게이지 3	게이지 44
걸음	(파운드)	με	με	με	με
1	0.00	1	1	1	0
2	1.10	83	56	-21	-87
3	2.21	163	115	-41	-171
4	3.31	243	171	-62	-254
5	4.42	325	228	-83	-338
6	5.52	400	280	-104	-423
7	6.62	485	338	-122	-501
8	7.73	557	386	-143	-589
9	8.83	634	442	-163	-665
10	9.93	714	502	-184	-741
11	8.83	637	445	-162	-664
12	7.73	561	391	-142	-584
13	6.62	483	335	-123	-506
14	5.52	406	281	-102	-423
15	4.42	323	227	-83	-339
16	3.31	245	171	-62	-256
17	2.21	164	115	-41	-170
18	1.10	83	56	-21	-87
19	0.00	1	0	1	2

표 1: 알루미늄 바의 균주.

게이지 팩터	1	2	3	최대 주체 변형	최소. 주 변형	각	푸아송의 비율
로드 스텝	με	με	με	(Eq. 9)	(Eq. 9)	(Eq. 10)	(Eq. 7)
1	1	1	1	1	1	0	0
2	83	56	-21	89	-26	-0.223	0.297
3	163	115	-41	176	-55	-0.243	0.311
4	243	171	-62	263	-82	-0.242	0.312
5	325	228	-83	351	-109	-0.240	0.311
6	400	280	-104	432	-136	-0.240	0.314
7	485	338	-122	523	-160	-0.237	0.307
8	557	386	-143	600	-186	-0.236	0.310
9	634	442	-163	684	-213	-0.238	0.312
10	714	502	-184	773	-242	-0.242	0.314
11	637	445	-162	688	-213	-0.239	0.309
12	561	391	-142	605	-186	-0.237	0.308
13	483	335	-123	520	-161	-0.236	0.309
14	406	281	-102	437	-133	-0.234	0.303
15	323	227	-83	349	-109	-0.241	0.313
16	245	171	-62	264	-81	-0.238	0.308
17	164	115	-41	177	-54	-0.239	0.302
18	83	56	-21	89	-26	-0.223	0.297
19	1	0	1	2	0	0.000	0.000
					평균의	-0.239	0.310

표 2: 주균 및 경사 각도.

표 2의 최대 및 최소 주균은 푸아송 의 비율에 대해 매우 선형 추세(R² = 0.999)를 표시하는 도 5에 플롯됩니다. 선의 경사에 해당하는 푸아송의 비율(0.31)에 대해 얻은 값은 알루미늄 및 기타 금속에 대한 대부분의 참조에서 주어진 0.30에 매우 가깝습니다.

그림 5: 푸아송의 비율에 해당하는 최대 및 최소 주 변형 사이의 선의 경사를 나타내는 주 변형 데이터입니다.

로제트 스트레인 게이지 데이터의 좋은 물리적 해석은 모어 원에 주균을 플로팅하여 얻을 수 있다(도 6). 7.4 lbs.의 최대 하중의 경우 여기에 표시된 세 가지 측정값은 x축에서 시계 반대 방향으로 약 27.4º (또는 2Φ)의각도로 시작하여 90º에서 서로 원의 3 점에 해당합니다.

그림 6: 변형에 대한 모어의 원에 표시된 변형 장미 값 판독의 물리적 중요성.

표 3은 빔의 밑면에 있는 단일 게이지로부터의 주인장 균주에 대한 결과(압축 중이지 4), 바닥과 최고 최대 주응사이의 비율, Eq.(11)의 응력 과 영의 변둘루스(E)의 응력 비율을 Eq로부터의 긴장비율로 나타낸다.(11). 표 3에서 영의 계수는 15개의 중간 로딩 단계에 대해 계산된 계골의 평균을 취하여 10147ksi로 계산됩니다.

	부하	최대. 교장. 거르다	최대 주체 스트레스	민 원스트레스	굽힘 응력	영'모둘루스
로드 스텝	파운드.	με	ksi	ksi	psi	ksi
1	0.00	1	10	9	0	0
2	1.10	89	886	0	882	9945
3	2.21	176	1765	0	1763	9991
4	3.31	263	2630	0	2645	10058
5	4.42	351	3513	0	3526	10038
6	5.52	432	4324	0	4408	10195
7	6.62	523	5230	0	5290	10113
8	7.73	600	6001	0	6171	10283
9	8.83	684	6843	0	7053	10307
10	9.93	773	7726	0	7935	10269
11	8.83	688	6877	0	7053	10256
12	7.73	605	6051	0	6171	10198
13	6.62	520	5204	0	5290	10165
14	5.52	437	4368	0	4408	10091
15	4.42	349	3494	0	3526	10092
16	3.31	264	2644	0	2645	10004
17	2.21	177	1770	0	1763	9960
18	1.10	89	886	0	882	9945
19	0.00	2	19	0	0	0
					평균의	10147

표 3: 탄성의 계수 계산(E).

E용 데이터는 또한 도 7에 플롯되어, 이는 응력과 스트레인 사이의 우수한 선형 관계(high^R2)와약 10,147 ksi의 경사를 나타낸다. 도 6의 경사면에 대한 계산은 요격이 0을 통과하도록 요구하기 때문에 표 3과 도 6의 계수의 차이가 발생합니다. 크기는 매우 호의적으로 비교됩니다(오류는 1.5% 미만) 일반적으로 10,000 ksi로 주어진 6061T6 알루미늄에 대한 E의 게시 값.

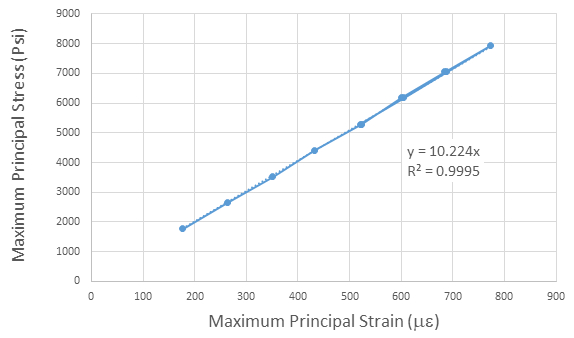
그림 7: 최대 응력 라인과 최대 균주의 경사는 영의 변성입니다.

마지막으로, Eqs를 다시 캐스팅하여. (5) 및 (6) 입력 :

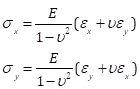(Eq. 12)

우리는 Mohr의 원을 사용하여 주 응력을 계산할 수 있습니다. 6.61 lbs.에 대응하는 단계의 경우, 주균(634, -189)의 주체는 (7.34, 0.00) ksi(도 8)의 주체응으로 이어집니다. 여기서 계산은 평면 응력에 대한 식을 사용하여 수행되지만, 결과는 주축을 따라 수직 방향의 응력이 0(또는 매우 가깝다)임을 나타내며, 이는 동축 적재의 경우에 해당합니다. 2Φ = 0.40 라디안의 각도로 응력 값은 (6.50, 2.82) ksi입니다.

그림 8: 7.34 파운드 부하의 경우 비행기 스트레스에 대한 모어의 원.

본 실험에서 탄성(E) 및 푸아송의비율(v)의계수를 측정하였다. 이 실험은 로제트 균주 게이지를 사용하여 실험실 환경에서 이러한 상수를 측정하는 방법을 보여줍니다. 획득한 값은 각각 10,000ksi 및 0.3의 게시된 값과 잘 일치합니다. 이러한 값은 엔지니어링 설계를 위한 탄성 이론을 적용하는 데 핵심적이며, 본원에 설명된 이 실험 기술은 재료 상수를 획득하는 데 사용되는 기술의 전형이다. 이러한 값을 얻으려면 고해상도 계측 및 추적 가능한 교정 절차를 활용하는 데 세심한 주의를 기울여야 합니다. 특히 스트레인 게이지 기반 장치와 16~24비트 디지털 데이터 수집 시스템의 사용은 이러한 실험의 성공과 품질에 필수적입니다.

오늘날, 파전파 방법(초음파 에코 펄스 방법) 및 나노 들여쓰기를 포함하여 영의 재료계수를 결정하는 다른 방법이 있습니다. 파도 전파를 활용하는 한 가지 이점은 영의 변조기를 측정하는 비파괴적 방법 중 하나이며, 나노핀덴션및 로제트 균주 게이지의 사용은 더 침습적인 방법이다.

토스터에서 마천루에 이르는 모든 엔지니어링 제품의 설계는 설계를 개선하고 최적화하기 위해 효과적인 분석 모델을 사용해야 합니다. 탄력이론은 토목 설계에 사용되는 대부분의 모델의 기초이며, 여러 상수의 설립을 기반으로합니다.

단일(또는 극소수의 복제) 복제만 빌드될 때 분석 모델이 필요합니다. 구조의 비용과 성능은 이러한 분석의 결과에 따라 달라지므로 이러한 분석은 재료 특성에 대한 강력한 값을 갖는 것에 따라 달라지므로 여기에 설명된 것과 같은 테스트는 시공 프로세스에서 품질 관리 및 품질 보증을 보장하기 위해 실행되어야 합니다. 예를 들어:

• 건물의 외관을 선택할 때, 건축가는 방수 봉투를 설계하는 데 주의해야합니다. 벽돌 건물 외관의 물 압박감은 다른 요인 들 중 균열되지 않은 벽돌 사이의 박격포를 유지하는 데 달려 있습니다. 박격포가 균열되면 물이 침투하여 부식 및 습도 문제를 일으켜 수정하기가 매우 비쌉습니다. 박격포가 균열되기 전에 저항할 수 있는 힘을 결정하기 위해서는 이론과 관련 상수가 모두 필요합니다. 건축가와 구조 엔지니어는 정면이 볼 수있는 부하 (자기 무게, 바람, 운전 비 등)와 각 설계 옵션이 이러한 조건에서 수행하는 방법을 결정하기 위해 함께 작동해야합니다. 그런 다음에야 적절한 특성을 가진 박격포를 선택해야 합니다.
• 버즈 두바이와 같은 고층 건물을 건설할 때 건설 회사는 바닥 층을 유지하는 데 세심한 주의를 기울여야 합니다. 시공이 진행됨에 따라, 기둥과 벽의 크기가 다른 경우, 이러한 요소 중 일부는 건설이 진행되고 더 많은 무게 (응력)가 추가됨에 따라 다른 요소들보다 더 단축 (균주)할 수 있습니다. 건설의 끝에 평면 바닥을 얻기 위해, 건설 회사는 낮은 층의 기둥과 벽의 높이에 조정해야합니다 - 낮은 층은 건설의 초기 단계에서 수준이 아닌 수 있지만 끝에 평평해야한다. 이러한 조정 방법을 제대로 계산하기 위해 건설 회사는 구조 엔지니어를 고용하여 차동 기둥과 벽 높이에 대한 데이터를 제공합니다. 엔지니어는 이러한 계산을 수행하기 위해 재료 상수를 사용해야 합니다.
• 소다 캔의 설계에서 제조업체는 알루미늄이 매우 비싼 재료이기 때문에 알루미늄 벽의 두께를 최소화해야합니다. 캔의 모양과 치수를 최적화하려면 제조업체가 중요한 로드 조건을 결정해야 합니다. 운송 및 보관 조건은 소비자의 음주보다 더 까다로운 일 수 있습니다. 이러한 조건의 대부분은 실험 테스트 프로그램 내에서 복제하기 어렵고 비용이 많이 들 것입니다. 제조업체는 프로토타입 단계로 이동하기 전에 캔 치수를 최적화하기 위해 많은 분석을 선택할 수 있습니다. 이 절차는 보잉이 드림라이너(보잉 787)를 개발하는 데 따랐습니다. 이러한 연구를 수행하려면 재료 특성을 알려야 하며 적절한 이론을 선택해야 합니다.