Dinámica de estructuras

Fuente: Roberto León, Departamento de Ingeniería Civil y ambiental, Virginia Tech, Blacksburg, VA

Hoy en día es raro que un año pasa sin un evento de terremoto causa estragos en algún lugar del mundo. En algunos casos, como el terremoto 2005 de Banda Ache en Indonesia, los daños involucrados grandes zonas geográficas y en las seis cifras de víctimas mortales. En general, el número y la intensidad de los terremotos no está aumentando, sin embargo, está aumentando la vulnerabilidad del entorno construido. Con el aumento de la urbanización no regulada en áreas sísmicamente activas, como el "cinturón de fuego," Circum-Pacífico Mar aumento en zona costera colocación bajo y aumentando las concentraciones de producción y distribución de energía y digital/telecomunicaciones nodos críticos de la red en zonas vulnerables, es claro que el diseño sismo-resistente es resiliencia comunitaria clave para el futuro.

Diseño de estructuras para resistir daños causados por terremotos ha progresado enormemente en los últimos 50 años, principalmente a través del trabajo en Japón tras el terremoto de Niigata de 1964 y en los Estados Unidos tras el terremoto del Valle de San Fernando de 1971. El trabajo ha avanzado a lo largo de tres vías paralelas: los trabajos experimentales encaminadas a desarrollar técnicas de construcción mejorado para minimizar el daño y la pérdida de la vida; (b) estudios analíticos basados en modelos materiales avanzados geométricos y no lineal; y, (c) síntesis de los resultados en (a) y (b) en disposiciones del código de diseño que mejoran la capacidad de las estructuras para resistir cargas inesperadas.

Pruebas sísmicas en un entorno de laboratorio es a menudo difícil y costoso. Prueba es sobre todo realizada utilizando las tres técnicas siguientes:

1. Prueba cuasi-estática (QST), donde partes de una estructura se prueban usando había aplicado lentamente y equivalente predeterminados deformaciones laterales con condiciones de contorno idealizadas. Esta técnica es particularmente útil para evaluar los efectos de detalles estructurales de la capacidad de resistencia y deformación de partes concretas de estructuras.
2. Prueba pseudo-dinámica de (PSDT), donde las cargas se aplican también lentamente, pero los efectos dinámicos se toman en cuenta resolviendo las ecuaciones de movimiento conforme avanza la prueba y mediante la utilización de prueba directa votos (sobre todo la rigidez instantánea) para evaluar la rigidez real y características de amortiguación de la estructura.
3. Sacuda las tablas, donde modelos a escala de estructuras completas son sometidos a movimientos con accionamiento hidráulico base o Fundación de entrada. Mesas de sacudidas representan un fiel más, prueba técnica, como la estructura artificial no es refrenada, la entrada es movimiento verdadero de la tierra y las fuerzas resultantes son realmente inercial, como era de esperar en un terremoto real. Sin embargo, las necesidades son enormes y sólo algunos sacudir tablas capaces de trabajar en casi a gran escala existen alrededor del mundo. Todo el mundo, hay sólo una tabla de sacudida grande capaz de llevar a cabo pruebas en las estructuras a gran escala, que es la mesa de sacudidas en las instalaciones de E-defensa de Japón, construido tras el terremoto de Kobe de 1985.

En este experimento, utilizamos un pequeño batido mesa modelo las estructuras y para estudiar las características de comportamiento dinámico de algunos modelos estructurales. Es estas características dinámicas, principalmente la frecuencia natural y amortiguamiento, así como la calidad de los detalles estructurales y la construcción, que hacen las estructuras más o menos vulnerable a los terremotos.

Hay una diferencia fundamental entre las habituales (uno mismo-peso) cargas gravitatorias que actúan sobre una estructura, que son cuasi-estático (es decir, cambian muy lentamente, o no con el tiempo) y los producidos por huracanes, explosiones y terremotos, que son extremadamente dinámico en la naturaleza. En el caso de los huracanes y otras cargas de viento, es posible modelar sus efectos como equivalente presiones estáticas en el laboratorio como la frecuencia de los vientos es muy largo comparada con la frecuencia natural fundamental de la estructura típica. Las excepciones a esto incluyen estructuras flexibles, como largo-palmo cable-permanecido, puentes colgantes, mástiles altos y estructuras de turbina de viento, donde la frecuencia natural de la estructura puede coincidir con las ráfagas de viento o recta vientos importantes. En el caso de los terremotos, las cargas son fundamentalmente inerciales como el suelo se mueve, y la estructura tiende a permanecer todavía. En este caso, la carga depende de la masa real, rigidez y amortiguamiento de la estructura, y las cantidades de interés son las aceleraciones, velocidades y desplazamientos alrededor de la estructura. Este segundo conjunto de cantidades es muy difícil reproducir con exactitud en el laboratorio si no se dispone de mesas de sacudidas.

Usando la física básica, como segunda ley de Newton, uno puede simplificar el problema del equilibrio de una estructura (como un puente o una estructura con viga rígida), que está sujeto a movimientos de tierra (u de_g), a la de una solo grado de libertad masa (m) rigidez (k) y características de amortiguación (c). Estos dos últimos pueden ser representado por un resorte en el cual la fuerza es proporcional al desplazamiento (u), así como un amortiguador en el que las fuerzas son proporcionales a la velocidad (v) (Figura 1). Estos componentes pueden combinarse en paralelo o en serie a diferentes configuraciones estructurales del modelo.

Rigidez se define como la fuerza requerida para deformar la estructura por un importe unitario. Supongamos que cargas un voladizo de la viga con una fuerza conocida (P) y medir su deformación elástica en la punta (). La rigidez se define como k = P /. Para el sistema voladizo elástico simple muestra, k = L³/3EI, donde L es la longitud del voladizo, es su momento de inercia, y E es módulo de Young para el material utilizado. A continuación, imaginar lo que sucede si uno quita la fuerza de repente, de tal modo permitiendo que el voladizo vibrar. Intuitivamente uno esperará la amplitud de las vibraciones para comenzar a disminuir en cada ciclo. Este fenómeno se denomina amortiguación y se refiere a una serie de complejos mecanismos internos, como la fricción, que tienden a reducir las oscilaciones. La cuantificación del amortiguamiento se describe más adelante en este laboratorio, pero es importante tener en cuenta que en este momento, no se sabe mucho acerca de estos mecanismos desde una perspectiva teórica o práctica. Un concepto útil es visualizar el coeficiente de amortiguamiento crítico (c_cr), que corresponde al caso donde el voladizo vendrá a descansar después de una oscilación completa.

Figura 1: Modelo de sistema único grado de libertad.

Escritura de una ecuación de equilibrio horizontal de fuerzas para el sistema mostrado en la figura 1 lleva a:

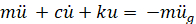(EC. 1)

Si nos fijamos en un caso más simple por un momento, donde podemos pasar por alto porque sus efectos son insignificantes, y no hay ninguna función de forzamiento externa de amortiguación, la ecuación 1 se convierte en la ecuación lineal homogénea de segundo orden diferencial:

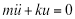(EC. 2)

cuya solución es de la forma:

(EC. 3)

Diferenciando dos veces nos dará:

(EC. 4)

Sustituyendo la ecuación 4 en la ecuación 2, produce:

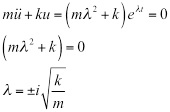(EC. 5)

La solución general es:

(EC. 6)

Donde es la frecuencia natural undamped del sistema.

Si este sistema se da un desplazamiento inicial () o una velocidad inicial (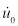), se convierte la ecuación 6:

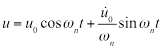(EQ. 7)

Si agregamos el efecto de amortiguación (c) y definir , la frecuencia natural amortiguada del sistema se convierte en y es el equivalente a la ecuación 7:

(EC. 8)

Para el caso de un desplazamiento inicial u₀, la figura 2 muestra el comportamiento de varios valores de .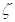

Figura 2: Efecto de amortiguación de las vibraciones libres: definición de amortiguamiento crítico (superior); cálculo del amortiguamiento de decremento logarítmico (inferior).

Si en la figura 2, se define , donde u_n y u_{n +}1 están el desplazamiento en ciclos sucesivos, entonces:

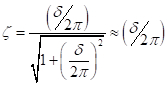(EC. 9)

Volviendo a la ecuación 1, si el movimiento de tierra se toma como la función sinusoidal 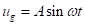, es el análogo de la ecuación 8:

(EC. 10)

Donde es el retraso de fase, y R_a es el factor de respuesta de amplificación, cuyas parcelas se ilustran en la figura 3. La figura 3 muestra que para valores bajos de amortiguación (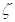 < 0,2), como la frecuencia de la función de forzamiento acerca a la frecuencia natural del sistema, la respuesta del sistema se vuelve inestable, un fenómeno que comúnmente se conoce como resonancia.

Figura 3: Respuesta de desplazamiento, velocidad y aceleración.

En este laboratorio, investigaremos experimentalmente los conceptos y derivaciones detrás de las ecuaciones 1 - 10 en el contexto de la dinámica de estructuras con una mesa vibradora.

1. modelos

1. Primero la construcción de varias estructuras de uso muy finos, fuertes, rectangulares, T6011 vigas de aluminio, 1/32 pulgadas de ancho y longitudes diferentes. Para construir el primer modelo, inserte una sola cantilever con longitud de 12 pulgadas para un bloque de madera muy rígido. Coloque una masa de 0,25 libras hasta la punta del voladizo.
2. Del mismo modo, construir otras estructuras modelo colocando ménsulas con diferentes longitudes en el mismo bloque de madera rígido. Coloque una masa de 0,25 libras hasta la punta de cada cantilever.
3. Preparar a dos otros especímenes simulando estructuras simples con columnas flexibles y pisos rígidos. Estos pueden ser construidos de finas placas de acero y diafragmas de piso de acrílico rígido. Una estructura será una historia de uno y otro serán dos historias. Los diafragmas de piso serán equipados con acelerómetros.

2. el aparato

Para estas demostraciones una pequeña mesa vibradora de tapa de tabla, multidisco, único grado de libertad se utilizará. El aparato consiste básicamente en una pequeña mesa metal cabalgando sobre dos rieles que es desplazada por un motor eléctrico. El desplazamiento es controlado digitalmente por un ordenador que puede de entrada periódicas (ondas sinusoidales) o aceleraciones aleatorias (preprogramada terremoto tierra de historias de tiempo de aceleración). Todo el control es a través de software propietario o software de tipo MatLab y Si mulLink. La entrada a función puede comprobarse comparando a la salida de un acelerómetro atado a la mesa.

3. procedimiento

1. Montar con cuidado el modelo con varios volados a la mesa de sacudidas, con pernos a base del modelo. Encienda la mesa vibradora y utilizando el software, incrementando lentamente la frecuencia hasta obtener la respuesta máxima de la estructura de cada cantilever. Tenga en cuenta que cada voladizo entra en resonancia a una frecuencia particular. Registrar en un cuaderno el valor de esta frecuencia. Seguir aumentando la frecuencia hasta que se reduzcan considerablemente los desplazamientos de los voladizos.
2. Montar la estructura del modelo de un piso a la mesa vibradora y repita el procedimiento. Poco a poco barrido a través de las frecuencias hasta que se alcanza la resonancia. Restablecer el software para ejecutar una historia suelo típico del tiempo aceleración (1940 El Centro) para mostrar los movimientos al azar que ocurren durante un terremoto.
3. Montar la estructura de dos pisos a la mesa vibradora y repita el procedimiento. Tenga en cuenta que dos frecuencias naturales se producen en este caso.

En primer lugar, determinar la frecuencia (ω) en el cual ocurrió el desplazamiento máximo para cada modelo. La original fórmula simple discutida arriba, 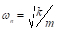, tiene que ser modificado porque la masa de la viga propia (m_b = W/g de_viga), que se distribuye sobre su altura, no es despreciable en comparación con la masa en la parte superior (m = W _bloque/g). La masa equivalente para el caso de una viga cantilever es (m + m 0,23_b), donde m es la masa en la parte superior y m_b es la masa distribuida de la viga. La rigidez k está dada por el recíproco de la deformación (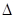) causados en la parte superior del voladizo por una fuerza de la unidad:

(EC. 11)

donde L es la longitud de la viga, E es el módulo de elasticidad, y es el momento de inercia . Da , donde b es el ancho y h es el espesor de la viga. Por lo tanto, es la frecuencia circular natural de una viga voladiza, incluyendo su uno mismo-peso:

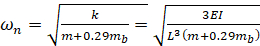(Eq.12)

Basado en esta ecuación, se calculan las frecuencias naturales previstas en la tabla 1.

De la viga número	Longitud (en)	Ancho (in.)	Espesor. (in.)	Me (in.4)	E (ksi)	Peso (libras)	Peso de la viga (lbs)	Masa efectiva (lbs-sec.2/en)	Frecuencia natural (ciclos por segundo)
1	12.0	1.002	0.124	1.59E-04	10200	0.147	0.149	4.70E-04	2.45
2	16.0	1.003	0.124	1.59E-04	10200	0,146	0.199	4.97E-04	1.55
3	20.0	1.002	0,125	1.63E-04	10200	0,146	0,251	5.28E-04	1.09
4	24.0	1.003	0,125	1.63E-04	10200	0.148	0.301	5.63E-04	0.80
5	28.0	1.001	0,125	1.63E-04	10200	0.144	0.350	5.82E-04	0.62
6	32.0	1.000	0.124	1.59E-04	10200	0,146	0.397	6.15E-04	0.49
7	36,0	1.002	0.126	1.67E-04	10200	0.147	0.455	6.52E-04	0,41
8	40.00	1.000	0,125	1.63E-04	10200	0.148	0.500	6.81E-04	0.34

Tabla 1: Frecuencias naturales de las vigas del voladizo probaron.

La medida y los valores teóricos de la frecuencia normal de nuestros sistemas modelo se comparan en la tabla 2. Se calcularon las frecuencias naturales reales cuidadosamente desplazando la viga voladiza por 1 pulgada y luego mirando el desplazamiento vs tiempo de respuesta. La comparación que más abajo se hacen en términos de períodos (T_d, en seg.) como estos se determinaron a partir de T_d = u₀u -₁, como se muestra en la figura 2(b). Esto requiere atención y paciencia para obtener resultados fiables. Las manifestaciones que se muestra sólo estaban destinadas a dar una ilustración general del comportamiento del sistema.

De la viga número	Frecuencia natural (ciclos por segundo)	Período previsto (seg.)	Período real (seg.)	Error (%)
1	2.45	2.56	2.65	-3.33%
2	1.55	4.06	4.23	-4.22%
3	1.09	5,78	6.79	-17.52%
4	0.80	7.84	8.04	-2.54%
5	0.62	10.06	10.63	-5.70%
6	0.49	12.79	13.04	-1,97%
7	0,41	15.32	16,78	-9.50%
8	0.34	18.59	20,56	-10.59%

Tabla 2. Comparación de los resultados.

Las diferencias se derivan principalmente del hecho de que las vigas no están rígidamente vinculadas a la base de madera, y la mayor flexibilidad en la base aumenta el período de la estructura. Otra fuente de error es que la amortiguación no correspondió en los cálculos, porque la amortiguación es muy difícil de medir y depende de la amplitud.

A continuación, de cada uno de desplazamiento vs historias de tiempo, extraer el máximo valor para cada frecuencia y trazar así la magnitud del desplazamiento vs frecuencia normalizada en la figura 3. Un ejemplo se muestra en la figura 4, donde hemos normalizado la frecuencia versus la primera frecuencia natural (rayo número 1) y trazar el desplazamiento máximo de la viga cuando la tabla de la sacudida fue sometida a una deformación variable sinusoidal con una amplitud de en 1.

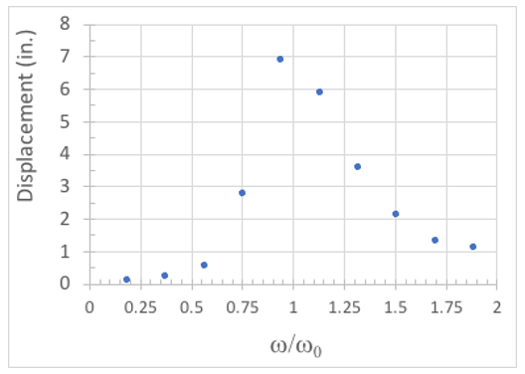
Figura 4 : Deformación de la viga #1 vs frecuencia normalizada tabla.

Inicialmente, cuando la relación de ω de ω/_n es pequeña, no hay mucha respuesta como la energía de entrada de la propuesta de mesa no excita el modelo. Como ω/ω_n se acerca a 1, hay un aumento muy significativo en la respuesta, con las deformaciones cada vez bastante grande. La respuesta máxima se alcanza cuando ω/ω_n está muy cerca de 1. A medida que la frecuencia normalizada aumenta más allá de ω/ω_n = 1, la respuesta dinámica comienza a morir; Cuando ω/ω_n se hace grande nos encontramos en una situación donde la carga se aplica muy lentamente con respecto a la frecuencia natural de la estructura, y la deformación debe ser igual a la de una carga estática aplicada.

El propósito de estos experimentos es principalmente mostrar los cambios en el comportamiento cualitativo, como se muestra en las manifestaciones de las dos estructuras. Obteniendo resultados similares a los de las figuras 3 y 4 requiere gran cuidado y paciencia como fuentes de fricción y similares afectará la cantidad de amortiguación y así cambiar las curvas similares a las de la figura 3(c) a la izquierda o derecha como real amortiguado frecuencia, 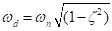, cambios.

En este experimento, la frecuencia natural y amortiguamiento de un sistema voladizo simple fueron medidos usando mesas de sacudidas. Aunque el contenido de frecuencia de un terremoto es aleatorio y cubre un gran ancho de banda de frecuencias, espectros de frecuencia se pueden desarrollar por traducir la historia de tiempo de aceleración en el dominio de la frecuencia mediante el uso de transformaciones de Fourier. Si las frecuencias predominantes del movimiento del suelo coincide con la de la estructura, es probable que la estructura sufrirá gran desplazamiento y por lo tanto estar expuesta a gran daño o incluso colapso. Diseño sísmico mira la forma espera que los niveles de aceleración un terremoto en un lugar determinado, basado en registros históricos, distancia a la fuente del terremoto, el tipo y tamaño de la fuente del terremoto, y la atenuación de la superficie y el cuerpo las ondas para determinar un razonable nivel de aceleración para diseño.

Lo que el público en general a menudo no se da cuenta es que las disposiciones actuales de diseño sísmico sólo sirven para minimizar la probabilidad de colapso y pérdida de vidas en el caso de que un terremoto máximo creíble se produce a un nivel aceptable (alrededor 5% a 10% en la mayoría casos). Mientras que los diseños estructurales para obtener menor probabilidades de fracaso son posibles, empiezan a ser antieconómico. Minimizando las pérdidas y mejorar la capacidad de recuperación después de un evento tan no explícitamente consideran hoy en día, aunque tales consideraciones se vuelven más comunes, como muchas veces el contenido de un edificio y su funcionalidad puede ser mucho más importante que su seguridad. Consideremos por ejemplo el caso de una planta de energía nuclear (como Fukushima en el 2011 el gran terremoto de Kanto), un edificio de diez pisos residencial en Los Angeles o un chip de ordenador de fabricación en Silicon Valley y su exposición y vulnerabilidad sísmica eventos.

En el caso de la planta de energía nuclear, puede ser conveniente diseñar la estructura para reducir al mínimo cualquier daño dado que la consecuencia de incluso un mínimo error puede tener consecuencias muy graves. En este caso, debemos intentar ubicar esta instalación lo más lejos posible de fuentes de terremoto para minimizar la exposición, ya que minimiza la vulnerabilidad hasta el nivel deseado es muy difícil y costoso. La realidad es que es prohibitivamente costoso hacerlo dado el deseo del público para evitar no solo un incidente tipo de Fukushima, pero también incluso una más limitada, como el desastre nuclear de Three Mile Island.

Para los varios pisos del edificio en Los Ángeles, es más difícil minimizar la exposición debido a una gran red de fallas sísmicas con periodos de retorno algo desconocidos está cerca, incluyendo la falla de San Andrés. En este caso, el énfasis debe estar en un diseño robusto y de detalle para minimizar la vulnerabilidad de la estructura; los propietarios de las residencias deben ser conscientes de que está tomando un riesgo significativo si ocurriera un terremoto. No deben esperar el edificio colapso, pero el edificio puede ser una pérdida completa si el terremoto es un suficiente magnitud.

Para la planta de chip de ordenador, los problemas pueden ser totalmente diferentes porque la estructura puede ser bastante flexible y fuera de la gama de frecuencias del terremoto. Así, la estructura no sufra ningún daño; sin embargo, puede dañarse severamente su contenido (equipamiento para la fabricación del chip), y podría interrumpirse la producción de la viruta. Según el conjunto específico de chips fabricados en la planta, el daño económico para el propietario de la instalación y a la industria como un todo puede ser tremendo.

Estos tres ejemplos ilustran por qué uno tiene que desarrollar estrategias de diseño resistente para nuestra infraestructura. Para alcanzar este objetivo necesitamos entender la entrada (movimiento de tierra) y la salida (respuesta estructural). Este problema sólo puede ser abordado a través de un enfoque combinado de analítico y experimental. El primero se refleja en las ecuaciones mencionadas, mientras que este último sólo puede lograrse mediante el trabajo experimental que se realiza a través de cuasi-estático, pseudo dinámico y agita tabla enfoques.