קבועי חומרים

המודל הנפוץ ביותר המשמש לניתוח הוא גמישות ליניארית (חוק הוק), אשר מניח כי שינויים בכוח (F) הם פרופורציונליים ישירות לשינויים בממד (Δ). בצורתו הפשוטה ביותר במקרים של טעינה חד-סקסית, כוח ו עיוות קשורים על ידי קבוע יחיד (E), או מודולוס של גמישות:

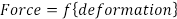(א"ק 1)

(א"ק 2)

(א"ק 3)

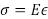(א"ק 4)

כפי שתואר במשוואות לעיל, הלחץ והמתח הם כמויות הנדסיות, בניגוד לכמויות אמיתיות. כמויות אמיתיות דורשות למדוד את השינויים הקטנים אך הסופיים בממדים המקומיים המתרחשים ככל שהכוחות גדלים. באופן ניסיוני, הישג זה קשה מאוד לביצוע, אפילו עם ההתקדמות האחרונה בטכנולוגיות מדידה ללא מגע. עבור חישובים אלה, ניתן להניח ששינויים אלה זניחים ומשתמשים באזור המקורי (A₀) ובאורך (L₀).

על מנת לקבוע את מודולוס האלסטיות מהמשוואות לעיל, יש צורך לקבוע את השינויים בכוח ובאורך כמו דגימה נטענת. בניסוי גס, אפשר להשתמש בקנה מידה אמבטיה וסרגל כדי לבצע משימות אלה. ראשית, אפשר לקחת גומייה עבה, למדוד את ממדיה ולסמן שתי נקודות על הרצועה המופרדת על ידי סנטימטר אחד. לאחר מכן, אפשר למקם מיכל פתוח על קנה מידה ולהוסיף מים עד הקריאה היא עשרה קילוגרמים. לאחר מכן ניתן להשעות את המיכל עם הגומייה ולמדוד כמה שני הסימנים הפרידו. מדידה זו תיתן לנו את כל הנתונים הדרושים לחישוב E עבור גומי שכן יש לנו את כל הערכים הדרושים כדי לפתור עבור E ב- Eqs. (2) עד (4). עם זאת, יהיו אי ודאויות גדולות מאוד ושגיאה הקשורים למדידה בגלל מכשיר המדידה הגס מאוד. מאז גודל המתח צריך להימדד עבור חומרי בנייה טיפוסיים הם בסדר גודל של 1x10^-6, מכשירי מדידה מדויקים בהרבה נחוצים כדי לקבוע קבועי חומר באופן ניסיוני. עבור רוב היישומים ההנדסיים הנפוצים, מדידות אלה מבוססות על בדיחות מאמץ התנגדות חשמלית. מכיוון שמכשירים אלה ישמשו לאורך הסרטונים הבאים, יינתן תיאור של עקרונות ההפעלה שלהם בהמשך.

גייג' זן הוא חוט לולאה ארוך המוטבע במטריצה נושאת (איור 2). גייג' המתח מודבק לחומר הנבדק עם אפוקסי בעל חוזק גבוה. כאשר החומר מעוות, החוטים ישתנו באורך והתנגדותם תשתנה מעט כתוצאה מכך. כאשר gage מוכנס כחלק ממעגל גשר Wheatstone, שינויים אלה ניתן לזהות כמו שינויים במתח. הופעתן של מערכות מדידה דיגיטליות הפחיתה במידה ניכרת את רעשי הרקע ומקורות שגיאה אחרים בתוך המעגל, ובכך שיפרה את הדיוק שבו ניתן למדוד את שינויי המתח כיום. gage המתח מכויל באמצעות קבוע המכונה גורם gage, כך הפלט שלה קשורה ליניארית למתח עבור טווח מאמץ נתון תחת קלט מתח נתון.

גייג' זן מודד את המתח בכיוון אחד בלבד. על מנת להשיג את מצב הלחץ המלא בנקודה על משטח, יש צורך בזן רוזט, המורכב משלושה בדיחות מאמץ המיושרות ב-45 מעלות זו לזו (איור 3). עם מדידות אלה בשלושה כיוונים שונים, ניתן להגדיר את כל מצב הלחץ על פני השטח באמצעות עקרונות כמו המעגל של מור לחישוב זנים עיקריים מקסימליים ומינימליים.

איור 2:זן גייג'.

איור 3: גייג' זן רוזט.

מדידות של כוח נעשות גם עם בדיחות מתח; עם זאת, מדידות אלה נלקחות בדרך כלל בתצורת גשר מלאה (כלומר, ההתנגדות הפנימית במעגל גשר וויטסטון מוחלפות על ידי בדיחות פעילות חיצוניות) וכתוצאה מכך התקן הנקרא תא עומס. תא העומס עצמו הוא בדרך כלל גליל פלדה עבה וחזק עם שתי בדיחות מותקנות לאורך ושניים מותקנים לרוחב כדי לחסל את ההשפעות של היחס של פואסון. הכיול של תא עומס דורש שימוש במשקלים מתים, כך שפלט המתח של המעגל יכול להיות קשור לעומס נתון. בארצות הברית, המכון הלאומי למדע וטכנולוגיה (NIST) מכייל תאי עומס של עד 5 מיליון קק"ל באמצעות משקולות מתות ומנגנוני ידית. כל תאי העומס המשמשים בארה"ב חייבים להיות ניתנים למעקב למקור כיול זה. בפועל, עקיבות פירושה שתא עומס A מכויל על-ידי NIST באמצעות משקולות מתות, נלקח למעבדות אחרות ומותקן בסדרה עם תא עומס B. לבסוף, תא עומס B מכויל בהתבסס על השוואת הפלט שלו לפלט של תא עומס A. יש לכייל מעת לעת את כל תאי הטעינה כדי לוודא שהם פועלים כראוי.

בדרך כלל, תא העומס מותקן במחשב בדיקה אוניברסלי (UTM). UTM מורכב ממסגרת תגובה עצמית עם שני עמודי בורג המופנים על ידי מנוע (איור 4). על ידי הידוק דגימת בדיקה לאחיזות UTM והפיכת עמוד הבורג כך שהראש הצולב נע כלפי מעלה, כוחות מתיחה מוחדרים לתוך הדגימה. הכוח המוחל נמדד על-ידי תא העומס, המותקן בסדרה עם הדגימה. מצד שני, אם מותקנים לוחות במקום ידיות מתיחה ועמודי הבורג מועברים כלפי מטה, כוחות דחיסה נכנסים לדגימה הבדיקה (כלומר, כדי לבדוק צילינדרים בטון).

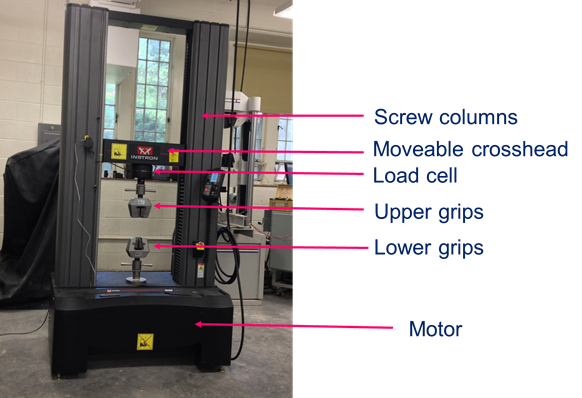
איור 4: מכונת בדיקה אוניברסלית.

כעת, לאחר שהוכח כיצד למדוד מתח וכוח, יידונו טיפול כללי יותר בתיאוריית האלסטיות. כשמסתכלים על פיסת מבנה כללית הנתינה לעומסים, אפשר לכתוב משוואות של שיווי משקל לכוחות ורגעים לאורך כל הצירים.

התוצאה היא סדרה של משוואות לזנים רגילים (ε) וגיסה (γ) של הצורה:

(א"ק 5)

(א"ק 6)

שש משוואות מסוג זה, שלוש לזנים רגילים (ε_x, ε_y ו- ε_z) ושלוש לזני גזוזים (γ_xy, γ_yz ו- γ_zx) נדרשים כדי לבסס את העיוותים הגלובליים. משוואות אלה מכילות שלושה קבועי חומר: מודולוס האלסטיות (E), היחס של פואסון (ν) ומודולוס הגניסה (G). כפי שמוצג במשוואה לעיל, מודולוס הגימור הוא השינוי בעיוות זוויתי בהתחשב בלחץ גיסת או מתיחה על פני השטח. היחס של פואסון מוגדר כ:

(א"ק 7)

ניתן להראות כי:

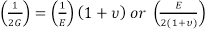= G (Eq. 8)

לפיכך, רק שניים מתוך שלושת הקבועים צריכים להיקבע, כדי להגדיר את כל השלושה. ישנם קבועים נגזרים רבים אחרים המשמשים בתורת האלסטיות, שכולם יכולים להיגזר ממדידות אלה. לדוגמה, מודולוס בתפזורת (B), או השינוי היחסי בנפח של גוף המיוצר על ידי יחידה דחיסה או מתח מתיחה מתנהג באופן אחיד על פני השטח שלה, הוא:

מאיקס. (5) ו -(6), ניתן לקבוע את מצב הלחץ והמתח על משטח אם מתבצעות לפחות שלוש מדידות זן עצמאיות. אם זן רוזט gage, אשר יש שלוש בדיחות ב 45 ° זה לזה (איור 3) משמש במקום gage אורך אחד, אז אפשר למצוא את הזנים העיקריים המרביים והמינימליים (ε₁, ε₂) ואת הזווית (Φ) בין הזנים הנמדדים ואת הזנים העיקריים מהמעגל של מור.

עבור גייג זן רוזט מלבני, כגון זה המוצג בתאנה 3 שבו הבדיחות הן ב 45 מעלות זה לזה:

(א"ק 9)

Φ =

טווח הזנים שעליהם מחזיקים יחסי האלסטיים הליניאריים הוא בין אפס לגבול היחסי של החומר. בניסוי זה, אשר ישתמש אלומיניום, מגוון הזנים יישמר הרבה מתחת לגבול זה.

נשתמש בקרן cantilever פשוטה עם בדיחות מאמץ כדי לעזור להמחיש את המושגים של מתח עיקרי ולחצים ואת החישוב של מודולוס של יאנג (E) ואת היחס של פואסון (ν).  קרן הקנטילוור תיטען בהדרגה עם סט משקולות והשינויים המתאימים בזן שנרשמו.  ניתן לחשב את הלחצים המתאימים ממשוואת הלחץ הפשוטה:

(א"ק 11)

כאשר M הוא הרגע (או הכוח המוכפל על ידי זרוע הידית שלו), c הוא המרחק מהמרכז לסיבים הקיצוניים בקורה על פני עומקו ( ), ואני רגע האינרציה, שניתן על ידי שבו b הוא רוחב הקרן ו- t הוא עוביו.

יש לייבא או לתמלל את הנתונים לגיליון אלקטרוני לצורך מניפולציה וגרף קלים. הנתונים שנאספו מוצגים בטבלה 1.

מכיוון שזן הרוזט אינו מיושר עם הצירים העיקריים של הקרן, זני הרוזט צריכים להיות קלט למשוואות עבור ε_1,2 (Eq. 9) ו- ε (Eq. 10) לעיל כדי לחשב זנים עיקריים, וכתוצאה מכך הנתונים המוצגים בטבלה 2. הטבלה מראה כי הזווית בין הלחץ הנמדד לבין הלחצים העיקריים היא על 0.239 רדיאנים או 13.7°. שים לב כי הזן העיקרי המרבי הוא חיובי, המתאים זן מתיחה גדול אורך; המתח העיקרי המינימלי הוא שלילי, המתאים לזן דחיסה רוחבי קטן יותר. היחס בין הזנים העיקריים המינימליים למקסימום מתאים ליחס של פואסון, המוצג בעמודה האחרונה וממוצע של כ-0.310.

	טען	גייג' 1	גייג' 2	גייג' 3	גייג' 44
צעד	(ק"ג)	με	με	με	με
1	0.00	1	1	1	0
2	1.10	83	56	-21	-87
3	2.21	163	115	-41	-171
4	3.31	243	171	-62	-254
5	4.42	325	228	-83	-338
6	5.52	400	280	-104	-423
7	6.62	485	338	-122	-501
8	7.73	557	386	-143	-589
9	8.83	634	442	-163	-665
10	9.93	714	502	-184	-741
11	8.83	637	445	-162	-664
12	7.73	561	391	-142	-584
13	6.62	483	335	-123	-506
14	5.52	406	281	-102	-423
15	4.42	323	227	-83	-339
16	3.31	245	171	-62	-256
17	2.21	164	115	-41	-170
18	1.10	83	56	-21	-87
19	0.00	1	0	1	2

טבלה 1: זנים בבר אלומיניום.

פקטור גייג'	1	2	3	מאמץ עיקרי מרבי	מינימום. זן עיקרי	פינה	היחס של פואסון
שלב טעינה	με	με	με	(א"ק 9)	(א"ק 9)	(א"ק 10)	(א"ק 7)
1	1	1	1	1	1	0	0
2	83	56	-21	89	-26	-0.223	0.297
3	163	115	-41	176	-55	-0.243	0.311
4	243	171	-62	263	-82	-0.242	0.312
5	325	228	-83	351	-109	-0.240	0.311
6	400	280	-104	432	-136	-0.240	0.314
7	485	338	-122	523	-160	-0.237	0.307
8	557	386	-143	600	-186	-0.236	0.310
9	634	442	-163	684	-213	-0.238	0.312
10	714	502	-184	773	-242	-0.242	0.314
11	637	445	-162	688	-213	-0.239	0.309
12	561	391	-142	605	-186	-0.237	0.308
13	483	335	-123	520	-161	-0.236	0.309
14	406	281	-102	437	-133	-0.234	0.303
15	323	227	-83	349	-109	-0.241	0.313
16	245	171	-62	264	-81	-0.238	0.308
17	164	115	-41	177	-54	-0.239	0.302
18	83	56	-21	89	-26	-0.223	0.297
19	1	0	1	2	0	0.000	0.000
					ממוצע	-0.239	0.310

טבלה 2: זנים עיקריים וזווית נטייה.

הזנים העיקריים המקסימליים והמינימליים מטבלה 2 משורטטים בתאנה 5 המציגה מגמות ליניאריות מאוד (R² = 0.999) ליחס של פואסון. הערך המתקבל עבור היחס של פואסון (0.31), התואם את השיפוע של הקו, קרוב מאוד ל-0.30 שניתן ברוב ההתייחסויות לאלומיניום ומתכות אחרות.

איור 5: נתוני המתח העיקריים המראים את שיפוע הקו בין זן עיקרי מרבי למינימום, התואם ליחס של פואסון.

ניתן להשיג פרשנות פיזית טובה לנתוני זן הרוזט מתווית הזנים העיקריים במעגל מור (איור 6). שים לב ששלוש המדידות, המוצגות כאן עבור המארז של העומס המרבי של 7.4 ליברות, תואמות לשלוש נקודות במעגל ב- 90 מעלות זו לזו, החל מזווית של כ- 27.4º (או 2Φ)נגד כיוון השעון מהציר x.

איור 6: משמעות פיזית של קריאות רוזט מאמץ המוצגות במעגל של מור למתח.

טבלה 3 מציגה את העומסים, את התוצאות של זן המתיחה העיקרי מהג'יאג' היחיד בחלק התחתון של הקרן (Gage 4, שנמצא בדחיסה), את היחס בין הלחצים העיקריים התחתונים והמקסימליים העליונים, הלחץ מ- Eq. (11) ומודולוס של יאנג (E) כיחס הלחץ מ- Eq. (11) חלקי הזן מ- Eq ( 9). בטבלה 3, מודולוס של יאנג מחושב כ- 10147 ksi על ידי לקיחת הממוצע של המודולי המחושב עבור 15 שלבי הטעינה הבינוניים.

	טען	מקסימום, מנהל. זן	מקסימום מתח עיקרי	מינימום מתח עיקרי	מתח כיפוף	מודולוס הצעיר
שלב טעינה	ליברות.	με	ksi	ksi	פסאיי	ksi
1	0.00	1	10	9	0	0
2	1.10	89	886	0	882	9945
3	2.21	176	1765	0	1763	9991
4	3.31	263	2630	0	2645	10058
5	4.42	351	3513	0	3526	10038
6	5.52	432	4324	0	4408	10195
7	6.62	523	5230	0	5290	10113
8	7.73	600	6001	0	6171	10283
9	8.83	684	6843	0	7053	10307
10	9.93	773	7726	0	7935	10269
11	8.83	688	6877	0	7053	10256
12	7.73	605	6051	0	6171	10198
13	6.62	520	5204	0	5290	10165
14	5.52	437	4368	0	4408	10091
15	4.42	349	3494	0	3526	10092
16	3.31	264	2644	0	2645	10004
17	2.21	177	1770	0	1763	9960
18	1.10	89	886	0	882	9945
19	0.00	2	19	0	0	0
					ממוצע	10147

טבלה 3: חישוב מודולוס של גמישות (E).

הנתונים עבור E מתווים גם ב- Fig. 7, המצביעה על קשר ליניארי מצוין (R^{גבוה 2}) בין מתח למתח ושיפוע של כ -10,147 ksi. ההבדל בין המודולוס משולחן 3 לבין זה מתוך איור 6 נובע משום שהחישובים עבור השיפוע ב- 6 דורשים שהיירוט יעבור דרך אפס. סדרי הגודל משווים לטובה רבה (שגיאה פחות מ-1.5%) עם ערכים שפורסמו של E עבור אלומיניום 6061T6, אשר ניתנת בדרך כלל כ- 10,000 ksi.

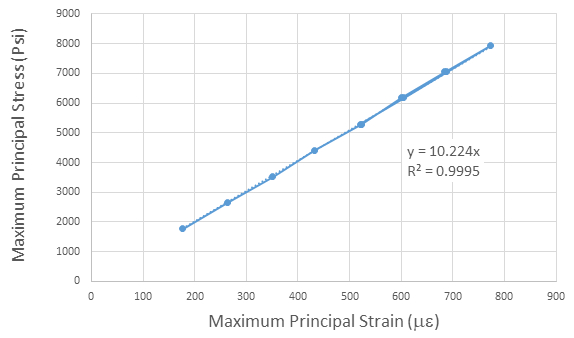
איור 7: שיפוע של קו הלחץ המרבי לעומת מקסימום המתח הוא המודולוס של יאנג.

לבסוף, על ידי ליהוק מחדש של Eqs. (5) ו-(6) לתוך:

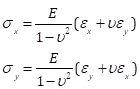(א"ק 12)

אנחנו יכולים לחשב את הלחצים העיקריים באמצעות המעגל של מור. במקרה של השלב המתאים ל 6.61 ק"ג של עומס, הזנים העיקריים של (634, -189) להוביל ללחצים עיקריים של (7.34, 0.00) ksi (איור 8). למרות החישובים כאן נעשים באמצעות הביטויים עבור מתח מישור, התוצאות מצביעות כראוי כי לאורך הציר העיקרי הלחץ בכיוון הניצב הוא אפס (או קרוב מאוד אליו), המתאים למקרה של טעינה חד-כיוונית. ערכי הלחץ בזווית של 2Φ = 0.40 רדיאנים הם (6.50, 2.82) ksi.

איור 8: המעגל של מוהר ללחץ מטוסים במקרה של עומס של 7.34 ק"ג.

בניסוי זה נמדדו שני קבועי חומר בסיסיים: מודולוס האלסטיות (E) והיחס של פואסון (v). ניסוי זה מדגים כיצד למדוד את הקבועים האלה בסביבת מעבדה באמצעות גייג זן רוזט. הערכים המתקבלים באופן ניסיוני תואמים היטב לערכים שפורסמו של 10,000 ksi ו- 0.3, בהתאמה. ערכים אלה הם המפתח ליישום תורת האלסטיות לתכנון הנדסי, וטכניקה ניסיונית זו המתוארת כאן אופיינית לאלה המשמשים להשגת קבועי חומרים. כדי להשיג ערכים אלה, יש לנקוט זהירות רבה הן בשימוש במכשור ברזולוציה גבוהה והן בהליכי כיול הניתנים למעקב. בפרט, השימוש במכשירים מבוססי gage זן ומערכות רכישת נתונים דיגיטליים 16 עד 24 סיביות הם חלק בלתי נפרד ההצלחה והאיכות של ניסויים כאלה.

כיום, ישנן שיטות אחרות לקביעת מודולוס של יאנג של חומר, כולל שיטות הפצת גל (שיטת הד-פולס קולי) ו nanoindentation. אחד היתרונות של ניצול התפשטות גלים הוא שזו אחת השיטות הלא הרסניות למדידת המודולוס של יאנג, בעוד ננו-אינפנטציה ושימוש בזן רוזט הם שיטות פולשניות יותר.

העיצוב של כל מוצר הנדסי, טוסטר לגורד שחקים, דורש שימוש במודלים אנליטיים יעילים כדי לשפר ולייעל את העיצוב. תורת האלסטיות היא הבסיס של רוב הדגמים המשמשים בתכנון ההנדסה האזרחית, והיא מבוססת על הקמתם של מספר קבועים.

מודלים אנליטיים נדרשים כאשר רק שכפול יחיד (או מעט מאוד) ייבנה. כמו העלות והביצועים של המבנה תלויים בתוצאה של ניתוחים אלה, ניתוחים אלה, בתורו, תלויים בערכים חזקים עבור המאפיינים החומריים, בדיקות כגון אלה המתוארות כאן חייבות להיות מופעלות כדי להבטיח בקרת איכות ואבטחת איכות בתהליך הבנייה. לדוגמה:

• בבחירת חזית לבניין, על האדריכל להקפיד על תכנון מעטפה עמידה למים. לחץ המים של חזית בניין לבנים עשוי להיות תלוי בשמירה על המרגמה בין הלבנים uncracked, בין היתר. אם המרגמה נסדקת, המים יחדרו ויגרמו לבעיות קורוזיה ולחות אשר יהיה יקר מאוד לתקן. על מנת לקבוע כמה כוח המרגמה יכולה להתנגד לפני שהיא נסדקת, אנחנו צריכים גם תיאוריה וגם הקבועים הקשורים אליה. האדריכל ומהנדס המבנים חייבים לעבוד יחד כדי לקבוע אילו עומסים אראה החזית (משקל עצמי, רוח, גשם נהיגה וכו ') וכיצד כל אפשרות עיצוב תתבצע בתנאים אלה. רק אז ניתן לבחור מרגמה עם המאפיינים המתאימים.
• בבניית בניין גבוה, כגון בורג 'דובאי, חברת הבנייה צריכה לשים לב היטב לשמירה על מפלס הקומות. ככל שהבנייה מתקדמת, אם גדלי העמודים והקירות שונים, חלק מהאלמנטים האלה עשויים לקצר (זן) יותר מאחרים ככל שהבנייה מתקדמת ומתווסף משקל רב יותר (מתח). כדי להשיג קומות שטוחות בסוף הבנייה, חברת הבנייה תצטרך לבצע התאמות לגובה העמודים והקירות בקומות התחתונות - הקומות התחתונות לא יכול להיות ברמה בשלבים הראשונים של הבנייה אבל צריך להיות שטוח בסוף. כדי לחשב כיצד לבצע כראוי התאמות אלה, חברת הבנייה תשכור מהנדס מבנים כדי לספק נתונים על עמודים דיפרנציאליים וגבהים בקיר. המהנדס יצטרך להשתמש בקבועי חומרים כדי לבצע חישובים אלה.
• בעיצוב של פחית סודה, יצרן חייב למזער את עובי קיר האלומיניום, כמו אלומיניום הוא חומר יקר מאוד. כדי למטב את הצורה והממדים של הפחיות, היצרן צריך לקבוע אילו תנאי טעינה חשובים; תנאי ההובלה והאחסון עשויים להיות תובעניים יותר מאשר הצרכן שותה ממנו. רבים מתנאים אלה יהיו קשים ויקרים לשכפול בתוך תוכנית ניסויים; היצרן עשוי לבחור לעשות הרבה ניתוח כדי לייעל את ממדי הפחית לפני המעבר לשלב אב הטיפוס. הליך זה הוא מה בואינג בעקבות בפיתוח דרימליינר (בואינג 787). כדי לבצע מחקרים אלה, תכונות חומריות חייבות להיות ידועות ואת התיאוריה המתאימה שנבחרה.