在多个方向向量
Overview
资料来源: 尼古拉斯 · 蒂蒙斯、 Asantha 库雷博士、 物理系 & 天文,物理科学学院,加利福尼亚大学,加利福尼亚州欧文市
本实验演示如何向量加法和减法在多个方向。目标将是解析计算加法或减法的多个向量,然后通过实验证实了计算。
一个向量是具有大小和方向的对象。矢量,简称长度,虽然通常由它与x轴的角度明确了方向。因为部队是向量,可以作为载体的物理表现。通过设置力系,找到哪些额外的力量将创造力量之间的平衡,可以实验验证系统的向量。
Principles
在图 1中显示的矢量 ,以及x和y轴和角度 θ,
,以及x和y轴和角度 θ, 与x-轴。
与x-轴。

图 1.
若要添加或减去两个向量,是有用来描述其x和y的成分向量。X-组件是指向x 轴方向,数学上表示为向量数目:
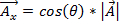 .(方程 1)
.(方程 1)
Y-组件表示为:
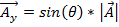 .(公式 2)
.(公式 2)
大小 被定义为:
被定义为:
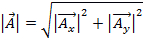 .(方程 3)
.(方程 3)
若要添加或减去两个向量,请简单向量分解成其x和y的组件然后添加或分别减去相应的组件。
例如,如果向量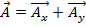 和矢量
和矢量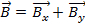 ,然后两个向量的加法
,然后两个向量的加法 。
。
若要确定一个向量所作出的关于x轴的夹角 θ,请使用以下公式:
 .(方程 4)
.(方程 4)
因为向量具有大小和方向,乘以两个向量是不简单,两个数字相乘。有两种方式,矢量乘法: 点积和叉积。点产品可以写成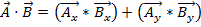 或
或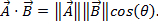 在这里,θ 是两个向量之间的夹角。结果仅有大小,又不有方向。点积在物理中应用是工作 (W),在那里工作定义为时间距离力
在这里,θ 是两个向量之间的夹角。结果仅有大小,又不有方向。点积在物理中应用是工作 (W),在那里工作定义为时间距离力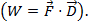 两个向量的叉积可以写成
两个向量的叉积可以写成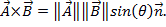 虽然相似点产品,跨产品包含词
虽然相似点产品,跨产品包含词 ,这定义为一个向量是垂直于两个向量的数值 1
,这定义为一个向量是垂直于两个向量的数值 1 和
和 。跨产品的结果是一个向量。物理学中的叉乘积的一个例子是扭矩
。跨产品的结果是一个向量。物理学中的叉乘积的一个例子是扭矩 ,这是一种力量的结果乘以半径
,这是一种力量的结果乘以半径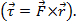
向量是物理学中有用的因为像重力或摩擦的部队可以表示为向量。在这个实验中,重力的作用用于展示的矢量性质的部队,这些部队在多个方向中的添加。在地球表面上的重力是写成:
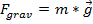 (方程 5)
(方程 5)
在 是质量的对象,而
是质量的对象,而 是靠近地球表面 (9.8 m/s2) 重力加速度。
是靠近地球表面 (9.8 m/s2) 重力加速度。
Procedure
1.平衡力量。
- 在力桌上,建立了两个滑轮与相同的质量面临着相反的方向 (角度 180 ° 差异)。
- 每个力将等于
 。检查两个部队是否平等和相反通过检查在力表,不应将移动的中心环。
。检查两个部队是否平等和相反通过检查在力表,不应将移动的中心环。 - 注意,是否添加的组件与这些部队有联系的向量的外力的矢量将有零级。这是如何确定所有力量都处于平衡状态。
2.分析计算。
- 这个实验室将包括三种力量的平衡。将已知两股力量,而第三个将会发现第一解析,使用理论的向量,然后通过实验。本实验中,为保持
 在 0 ° 的持续时间。
在 0 ° 的持续时间。 - 请注意,如果
 和
和 已知和
已知和 ,当添加到系统,原因两种力量处于平衡状态,然后
,当添加到系统,原因两种力量处于平衡状态,然后 是相等的巨大但方向相反的总和 (
是相等的巨大但方向相反的总和 ( +
+  )。
)。 - 计算的大小
 和
和 。使用这一事实,
。使用这一事实, 和 1 牛顿 (N) 是一个单位的力等于
和 1 牛顿 (N) 是一个单位的力等于 。
。 - 使用的载体,理论计算什么震级
 如果是总和会 (
如果是总和会 ( +
+  )。
)。 - 用的载体,理论计算什么角
 如果是总和会 (
如果是总和会 ( +
+  )。
)。
3.实验。
- 值如下表 1的第一行
 和
和 ,建立了力桌上的两股力量。记住要保持
,建立了力桌上的两股力量。记住要保持 在 0 °。
在 0 °。 - 建立了第三种力量,
 ,通过添加权重和改变角度,直到达到平衡。在表 2中记录这些值。
,通过添加权重和改变角度,直到达到平衡。在表 2中记录这些值。 - 每个四例重复步骤 3.2。
- 通过计算来确定从分析结果的差异百分比
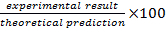 。完成这些计算值与表 2 。
。完成这些计算值与表 2 。
Results
实验室的结果所示表 1和表 2。
表 1。安装程序。
| 设置 # | A | B | ||
| 质量 | 角度 | 质量 | 角度 | |
| 1 | 100 | 0 | 100 | 20 |
| 2 | 100 | 0 | 150 | 40 |
| 3 | 200 | 0 | 150 | 60 |
| 4 | 200 | 0 | 250 | 80 |
表 2。分析的结果。
| 设置 # | 震级 (N) |
震级 (N) |
角度 (°) |
震级 (N) |
角度 (°) |
| 1 | 0.98 | 0.98 | 20 | 1.93 | 10 |
| 2 | 0.98 | 1.47 | 40 | 2.31 | 24 |
| 3 | 1.96 | 1.47 | 60 | 2.98 | 25 |
| 4 | 1.96 | 2.45 | 80 | 3.39 | 45 |
表 3。实验的结果。
| 设置 # | 实验规模 (N) |
分析震级 (N) |
差异 (%) |
实验的角度 (°) |
分析视角 (°) |
差异 (%) |
| 1 | 2.1 | 1.93 | 9 | 11 | 10 | 10 |
| 2 | 2.2 | 2.31 | 5 | 26 | 24 | 8 |
| 3 | 2.8 | 2.98 | 6 | 28 | 25 | 12 |
| 4 | 3.5 | 3.39 | 3 | 43 | 45 | 5 |
实验的结果相一致的分析计算。可以使用1 5 方程计算的两个向量和它们之间的角度总和。方程是有效的物理载体,如力的计算。
Application and Summary
在棒球外的野手已经了解向量,以在移动接球。如果外场手只知道球的速度,他可能会跑到右边而不是谈和错失良机。如果他只知道命中的方向,他可能会收取费用,只看球飞过他的头。如果他了解向量,然后尽快打了球,他可以考虑的大小和方向以估计球的去向他合理捕捞时。
当一架飞机在天空中,其速度和方向都可以写成一个向量中。时一阵大风,风矢量将添加到飞机给合成系统向量的向量。例如,如果一架飞机飞入风,综合矢量的大小将初始大小小于。这对应于飞机慢时进入的风,它产生的直观感觉。
当两个对象发生碰撞并粘在一起时,他们最终的动量矩 (矢量) 可以近似为两个初始动量向量的总和。这是一种简化,在现实世界中,碰撞的两个对象具有额外的因素要考虑,比如热或从碰撞变形。动量是只是其速度乘以物体的质量。如果两名选手在旅行中不同的方向和速度不同的冰上碰撞并紧紧抓住彼此,可以估计部分他们最终的方向和速度根据其初始向量组件。
在这个实验中,部队的矢量性质是检查,测量。向量加在一起,和合力的大小和方向,确定了分析和实验研究。
Tags
跳至...
此集合中的视频:

Now Playing
在多个方向向量
Physics I
182.3K Views

牛顿的运动定律
Physics I
75.7K Views

力和加速度
Physics I
79.1K Views

运动学和抛体运动
Physics I
72.6K Views

牛顿的万有引力定律
Physics I
190.9K Views

动量守恒
Physics I
43.3K Views

摩擦
Physics I
52.9K Views

胡克的法律和简谐运动
Physics I
61.3K Views

平衡和自由体图
Physics I
37.3K Views

扭矩
Physics I
24.4K Views

转动惯量
Physics I
43.5K Views

角动量
Physics I
36.2K Views

能源和工作
Physics I
49.7K Views

焓
Physics I
60.4K Views

熵
Physics I
17.6K Views
版权所属 © 2025 MyJoVE 公司版权所有,本公司不涉及任何医疗业务和医疗服务。