Fonte: Alexander S Rattner, Sanjay Adhikari e Mahdi Nabil; Departamento de Engenharia Mecânica e Nuclear, Universidade Estadual da Pensilvânia, Parque Universitário, PA

O aquecimento controlado seguido de resfriamento rápido é um elemento importante de muitas aplicações de processamento de materiais. Este procedimento de tratamento térmico pode aumentar a dureza do material, que é importante para cortar ferramentas ou superfícies em ambientes de alto desgaste. O estágio de resfriamento rápido é chamado de saciamento, e muitas vezes é realizado por materiais imersos em um banho fluido (muitas vezes água ou óleo). A saciação da transferência de calor pode ocorrer devido à convecção forçada - quando a ação do material em movimento rápido através do refrigerante impulsiona o processo de transferência de calor, e devido à convecção livre - quando a densidade reduzida de fluido quente perto da superfície do material causa circulação orientada pela flutuação e transferência de calor. Em altas temperaturas materiais, o refrigerante pode ferver, levando a um aumento da eficácia da transferência de calor. No entanto, quando materiais extremamente quentes são extintos, eles podem ser cobertos em vapor de refranhante de condutividade térmica relativamente baixa, levando à má transferência de calor.

Neste experimento, a transferência de calor será medida para um cilindro de cobre aquecido, que representa pequenas peças tratadas pelo calor. O perfil de temperatura da amostra transitória será medido durante a extinção e comparado com os resultados teóricos para transferência gratuita de calor de convecção. Fenômenos de ebulição também serão investigados qualitativamente.

O processo de saciar a transferência de calor é fundamentalmente transitório. Em geral, a distribuição da temperatura pode variar no espaço e no tempo dentro de uma amostra de material resfriado. No entanto, se a resistência térmica de condução interna for pequena em comparação com a resistência térmica externa da superfície da amostra ao fluido circundante (convecção), a amostra pode ser assumida como ter temperatura quase uniforme em qualquer instante, simplificando a análise. Essa condição pode ser expressa em termos do número Biot (Bi), que compara a resistência à condução interna à resistência à convecção externa. Geralmente, quando Bi < 0,1, a resistência à transferência interna de calor pode ser assumida insignificante em comparação com a resistência à transferência de calor externa.

(1)

Aqui, h é o coeficiente de convecção externa, k_s é a condutividade térmica da amostra, e L_c é uma escala de comprimento característica da amostra. h pode ser previsto usando modelos de transferência de calor e ajustes de curva publicados na literatura para diferentes condições e fluidos. Neste experimento, h será medido e comparado com os resultados previstos com os modelos publicados (ver seção Resultados Representativos).

Para o cilindro de cobre considerado aqui (k = 390 W m^-1 K^-1, diâmetro D = 9,53 mm, comprimento L = 24 mm), a escala de comprimento característico é D/2 = 4,8 mm. Assumindo um coeficiente máximo de convecção de h = 5000 W m^-2 K^-1, o número máximo de Biot seria de 0,06. Como este número é pequeno (< 0,1), é razoável supor que as resistências de condução interna são insignificantes, e a amostra tem temperatura uniforme. Em valores bi mais elevados, é necessária uma análise mais complicada que explica a variação de temperatura no material.

Assumindo uma amostra de temperatura uniforme, a taxa de transferência de calor pode ser modelada equilibrando a perda de energia interna da amostra com a taxa de remoção de calor convectiva da lei de resfriamento de Newton. Esta abordagem é chamada de análise de capacitância agrupada.

(2)

Aqui, m é a massa amostral (15 g), c é o calor específico do material amostral (385 J kg^-1 K^-1 para cobre), T_s é a temperatura amostral, As é a área_da superfície amostral (8,6 × 10^-4 m²), e é a temperatura do fluido circundante.

Para prever a taxa de resfriamento (dT s/dt) durante a extinção, o coeficiente de convecção (h) também deve ser previsto. Se a amostra estiver abaixo da temperatura de ebulição do fluido e mantida estacionária em uma piscina de refrigerante, então o calor é removido principalmente por convecção gratuita. Neste modo, a circulação e o resfriamento são produzidos pelo aumento de fluido aquecido perto da amostra. Maiores diferenças de temperatura amostra-fluido resultam em aumento das taxas de circulação.

Se a temperatura da amostra estiver acima do ponto de ebulição, o vapor pode ser gerado na superfície, resultando em taxas de resfriamento significativamente mais altas. Durante a ebulição, bolhas de vapor se formam e crescem a partir de pequenas imperfeições (locais de nucleação) na superfície quente. Em temperaturas superficiais mais altas, mais locais de nucleação se tornam ativos, resultando em maior coeficientes de convecção e maiores taxas de transferência de calor. No entanto, a temperaturas muito altas, o vapor de condutividade relativamente baixo não pode ser removido rápido o suficiente. Isso resulta na crise de ebulição,na qual o resfriamento da superfície é limitado devido ao isolamento de vapor, reduzindo a taxa de transferência de calor.

NOTA: Este experimento usa aquecimento de chamas. Certifique-se de que um extintor de incêndio está à mão e que nenhum material inflamável está perto do experimento. Siga todas as precauções padrão para a segurança contra incêndios.

1. Fabricação de amostra para saciar (ver fotografia, Fig. 1)

1. Corte um pequeno comprimento (~24 mm) de 9,53 mm de altura da haste de cobre. Faça dois pequenos furos (1,6 mm de diâmetro) a meio caminho da haste perto das duas extremidades. Esses buracos serão os poços termopar. Como os buracos e termoparles são relativamente pequenos, podemos supor que eles têm um efeito mínimo sobre o comportamento geral de transferência de calor.
2. Use epóxi de alta temperatura (por exemplo,JB Kwik) para fixar sondas termopar de alta temperatura nos dois orifícios. Certifique-se de que as pontas da sonda termoparple são pressionadas no centro da amostra de cobre à medida que os conjuntos epóxi.
3. Coloque um recipiente de água como um banho de saciamento. Insira um terceiro termopar de referência no banho perto de onde a amostra será saciada.
4. Conecte os três termopares a um sistema de aquisição de dados. Configure um programa (no LabVIEW, por exemplo) para registrar medições transitórias de temperatura em uma planilha.

Figura 1: a. Fotografia de amostra de cobre instrumentada no banho de água de resfriamento.b. Amostra de cobre aquecedor.

2. Realizar experimentos

1. Posicione um queimador de Bunsen ou um recipiente de combustível chafing ao lado do banho de saciamento. Acenda a chama.
2. A partir de uma distância segura de retenção, aqueça gradualmente a amostra sobre a chama (até ~50°C recomendado para o primeiro experimento). A amostra pode ser mantida pelos condutores termopar (Fig. 1b).
3. Comece a registrar os dados do termopar para arquivar e mergulhe a amostra no banho de saciamento. Mantenha a amostra estável para que a transferência de calor de convecção forçada seja mínima. Pare de registrar dados de temperatura assim que a amostra se aproximar dentro de alguns graus da temperatura do banho.
4. Repita este procedimento para temperaturas amostrais iniciais progressivamente mais altas (até ~300°C). Para casos acima de 100°C, observe o comportamento de ebulição após a saciação da amostra.

3. Análise de dados

1. Para as medidas de temperatura registradas, registo da temperatura média da amostra em cada momento como a média aritmética das duas leituras termopar incorporadas.
2. Calcule a taxa de resfriamento da amostra a cada hora registrada j as 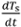= (T_s,j+1-T_s,j)/(t_j+1-t_j) (os valores serão negativos). Aqui, t_j é o tempo de cada leitura registrada. Pode ser útil suavizar essas curvas de taxa de resfriamento realizando uma média de funcionamento com uma janela de amostra de 2-3 leituras.
3. Calcule os coeficientes experimentais de transferência de calor h com Eqn. 2 utilizando a taxa de resfriamento da Etapa 3.2, e banho medido(T_∞) e temperaturas amostrais(T_s). Como esses coeficientes de transferência de calor se comparam com os valores previstos (Eqn. 4, ver Resultados)?
4. Para um caso com temperatura inicial abaixo de 100°C, use a medição inicial de temperatura experimental e integre numericamente Eqn. 2 para prever o resfriamento ao longo do tempo. Use Eqn. 4 para prever o coeficiente de convecção a cada momento. Compare esta curva com valores medidos. Para tamanho de etapa de tempo numérico Δt (por exemplo,0,1 s), a temperatura pode ser integrada como:
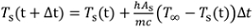   (3)

Fotografias de ebulição a diferentes temperaturas iniciais da amostra(T_s,0) são apresentadas em Fig. 2. Em T_s,0 = Bolhas de vapor de 150°C formam-se e permanecem presas à amostra. Em T_s,0 = bolhas de 175°C se desprendem e flutuam na água. A 200°C, mais bolhas são geradas, e aumentos adicionais são observados em temperaturas mais altas. Eventos do tipo crise de ebulição (por exemplo,amostras inteiras sendo cercadas por vapor persistente) não são observados devido à baixa temperatura do fluido a granel (~22°C).

Quando a temperatura da amostra estiver abaixo da temperatura de ebulição do refrigerante (100°C), modelos de convecção sem fase única podem ser aplicados para prever o coeficiente de convecção. A taxa de transferência de calor de convecção gratuita depende do número de Prandtl fluido (Pr), que é a razão da viscosidade à difusividade térmica (Pr = 6,6 para água à temperatura ambiente) e o número de Rayleigh (Ra), que é uma medida de transporte de convecção natural:

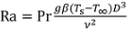(4)

Aqui, g é a aceleração gravitacional (9,81 m s^-2), β é o coeficiente de expansão térmica do fluido (mudança relativa na densidade com temperatura, 2,28 × 10^-4 K^-1 para água), e é o fluido viscosidade cinemática (9,57 × 10^-7 m² s^-1 para água). Como exemplo, para a amostra de 9,5 mm de diâmetro em T_s = 75°C em água em T_∞ = 22°C, o número de Rayleigh é Ra = 7,44 × 10⁵.

Para um cilindro horizontal em transferência de calor de convecção livre em fase única, uma fórmula de convecção amplamente utilizada (baseada em curvas se encaixa em dados empíricos) é apresentada na Equação 4.

(5)

Aqui, k é a condutividade térmica fluida (0,60 W m^-1 K^-1 para água). A fórmula dá o número Nusselt (Nu), o coeficiente de transferência de calor de convecção azíltico. Pode ser convertido ao coeficiente de transferência de calor dimensional (h nas unidades W m^-2 K^-1) multiplicando-se por k/D. Para o exemplo com Ra = 7,44 × 10⁵, este modelo prevê Nu = 16,4 e h = 1040 W m^-2 K^-1.

Na Fig. 3, os coeficientes de convecção instantâneo medidos são comparados com os valores teóricos de convecção livre da Equação 4. A concordância qualitativamente próxima é observada em temperaturas superficiais mais baixas(T_s-T_∞ < 80 K). Em temperaturas amostrais mais altas, ocorre esbulição e valores medidos de coeficiente de transferência de calor excedem significativamente as previsões de convecção livre de fase única. O coeficiente de convecção aumenta acentuadamente com a temperatura da amostra em condições de ebulição. Esse aumento deve-se ao maior número de locais de nucleação ativa em temperaturas superficiais mais altas.

Na Fig. 4, curvas de resfriamento de amostras medidas e previstas são apresentadas para um caso com temperatura inicial de 42,5°C. Inicialmente, a curva experimental de temperatura decai mais rápido. Isso pode ser devido a efeitos de convecção forçada de inserir a amostra no banho. Com o tempo, pequenas oscilações na curva medida são observadas, possivelmente devido ao movimento da pessoa que segura a amostra. Mais tarde, as curvas de temperatura experimentais e previstas combinam bem.

Figura 2: Fotografias de fenômenos de ebulição na amostra saciada a uma temperatura inicial aumentada (T₀)

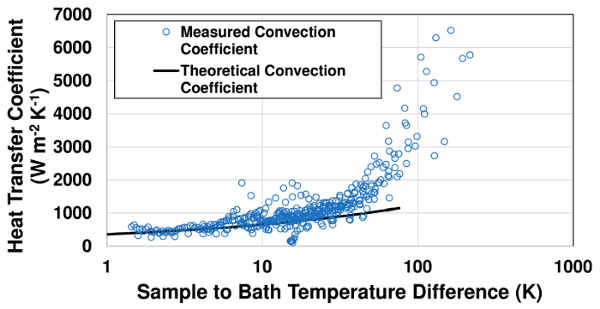
Figura 3: Comparação de convecção livre medida e coeficientes de convecção fervente com valores teóricos de convecção livre

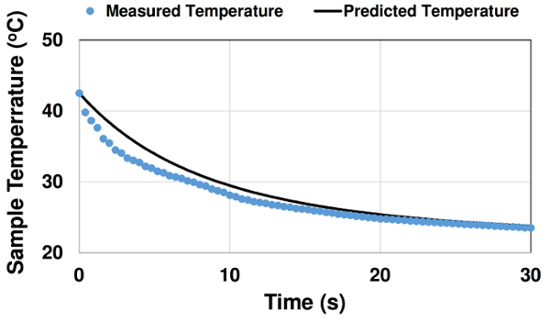
Figura 4: Comparação da curva de resfriamento medida e prevista para caso com temperatura inicial T₀ = 42,5°C

Este experimento demonstrou o processo de transferência de calor transitório durante a extinção. A temperatura de uma amostra de material foi rastreada, pois foi rapidamente resfriada em um banho de água. Os coeficientes de convecção e os perfis de temperatura ao longo do tempo foram comparados com valores teóricos para resfriamento gratuito de convecção. Fenômenos de ebulição também foram discutidos e observados para altas temperaturas iniciais da amostra. Informações de tais experimentos e abordagens de modelagem demonstradas podem ser aplicadas para entender e projetar processos de transferência de calor para fabricação e tratamento de calor de materiais.

O resfriamento rápido é frequentemente empregado em ferramentas de tratamento térmico. Certas ligas de aço podem ser enlatadas (aquecidas e gradualmente resfriadas) para reduzir a dureza para usinagem e trabalho. Eles podem então ser aquecidos e rapidamente resfriados para obter alta dureza para cortar outros materiais (por exemplo,arquivos, lâminas de serra) ou em aplicações de alto desgaste(por exemplo,cabeças de martelo, socos). Operações adicionais de tratamento térmico podem melhorar a dureza para evitar falhas frágeis.

De forma mais geral, o aquecimento e o resfriamento transitórios rápidos são encontrados em muitas aplicações. Por exemplo, os processadores de computador aquecem rapidamente ao executar programas computacionalmente intensivos. Esse aumento de temperatura muitas vezes provoca aumento da velocidade dos ventiladores e resfriamento rápido. Quando as usinas são acionadas, os tubos geradores de vapor experimentam um aquecimento rápido. Em ambos os casos, a previsão e a caracterização das taxas de aquecimento e resfriamento são importantes para evitar que os materiais falam devido ao superaquecimento e fadiga. As análises transitórias de transferência de calor, como demonstrado nesta investigação, são fundamentais para a engenharia dessas tecnologias.