Conservación del momento

Fuente: Nicolás Timmons, Asantha Cooray, PhD, Departamento de física & Astronomía, Facultad de ciencias física, Universidad de California, Irvine, CA

El objetivo de este experimento es poner a prueba el concepto de la conservación del ímpetu. Estableciendo una superficie con muy poca fricción, se pueden estudiar colisiones entre objetos en movimiento, incluyendo sus ímpetus iniciales y finales.

La conservación del ímpetu es una de las leyes más importantes en la física. Cuando algo se conserva en la física, el valor inicial es igual al valor final. Impulso, esto significa que el ímpetu inicial total de un sistema será igual al ímpetu total final. Segunda ley de Newton establece que la fuerza sobre un objeto será igual al cambio en el ímpetu del objeto con el tiempo. Este hecho, combinado con la idea de que el impulso se conserva, sustenta el funcionamiento de la mecánica clásica y es una poderosa herramienta para resolver problemas.

Impulso se define como la masa de un objeto veces su velocidad :

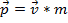. (Ecuación 1)

Uno puede también definir impulso en términos de las fuerzas que actúan sobre un objeto (la segunda ley de Newton):

. (Ecuación 2)

Aquí, 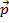es el impulso inicial y es el impulso final, con la misma Convención utilizada por vez y . La suma de las fuerzas que actúan sobre un objeto es igual al cambio en el ímpetu del objeto con el tiempo. Por lo tanto, si hay no hay fuerza neta actuando sobre un objeto, el cambio en el ímpetu será cero. Dicho de otra forma, en un sistema cerrado con ninguna fuerza externa, el impulso inicial será igual que el impulso final.

Este concepto se entiende más fácilmente en el contexto de colisiones unidimensionales y bidimensionales. Colisiones unidimensionales, un objeto con masa e inicial velocidad choca con otro objeto con masa e inicial velocidad 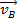. En estas colisiones, asumimos las fuerzas externas a ser demasiado pequeño para tener un efecto. En el laboratorio, una pista de aire se utiliza para reducir la cantidad de fricción, una fuerza externa, en los planeadores. Si el impulso inicial es igual al impulso final, entonces:

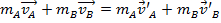, (Ecuación 3)

donde las velocidades cebadas representan que velocidades finales y las velocidades no cebadas representan las velocidades iniciales.

Figura 1 . Disposición experimental.

1. entender el temporizador fotopuerta.

1. Utilización de una balanza, medir y registrar la masa de cada vela.
2. Colocar una vela en la pista con un temporizador fotopuerta.
3. Ajustar el temporizador fotopuerta a la posición de "puerta".
4. Cuando la vela pasa a través de la fotopuerta, registrará el tiempo en que la bandera por encima de la vela pasa a través de la puerta. En un viaje de regreso, la fotopuerta no mostrará un nuevo tiempo. Interruptor de la palanca para "leer" para que mostrará el tiempo inicial más el tiempo de la segunda pasa por la puerta.
5. La bandera es de 10 cm de largo; determinar la velocidad de la vela con el hecho de que la velocidad es distancia dividida por tiempo.
6. Enviar el planeador a través de la fotopuerta varias veces, incluyendo los viajes de vuelta después de que ha rebotado de la pared y medir las velocidades con el fin de familiarizarse con el equipo. Recuerda que la velocidad tiene una dirección. Que la dirección de la velocidad inicial representan positivo y sentido contrario representan valores de velocidad negativa.

2. dos velas de igual masa.

1. Colocar dos planeadores y dos temporizadores fotopuerta en la pista, como en la figura 1.
2. Utilizar la ecuación 3 para determinar la expresión para la velocidad final. En esta parte del experimento, planeador B comenzará del resto.
3. Planeador de dar una cierta velocidad inicial para ello chocarán con vela B. registro la velocidad inicial de vela A, así como las velocidades finales de cada vela. Hacer esto tres veces, registre sus resultados y compararlos con la predicción teórica.

3. dos planeadores de masa desigual.

1. Añadir 4 pesos a planeador B, que serán el doble de su masa. Repita los pasos 2.1-2.3.

4. iguales masas, no a partir de resto

1. Retire el peso del planeador B.
2. Repita los pasos 2.1-2.3, pero Dale planeador B una velocidad inicial, en la dirección de vela A.

Tabla 1. Resultados de dos planeadores de igual masa.

Planeador (ensayo)	(cm/s)	(cm/s)	(cm/s)	(cm/s)	Diferencia (%)
UN (1)	72,5	-0.2	-	-	-
B (1)	0.0	67.1	72,5	66.9	8
A (2).	35,6	0.3	-	-	-
B (2)	0.0	37.4	35,6	37.7	6
(3)	47.4	0.0	-	-	-
B (3)	0.0	47.8	47.4	47.8	1

Tabla 2. Resultados de dos planeadores de masa desigual.

Planeador (ensayo)	(cm/s)	(cm/s)	(kg cm/s)	(kg cm/s)	Diferencia (%)
UN (1)	52.9	-10.7	-	-	-
B (1)	0.0	37.7	52.9	64.7	22
A (2).	60.2	-13.2	-	-	-
B (2)	0.0	41.5	60.2	69.8	16
(3)	66.2	-12.0	-	-	-
B (3)	0.0	45.9	66.2	79.7	20

Tabla 3. Resultados de masas iguales, no a partir de resto.

Planeador (ensayo)	(cm/s)	(cm/s)	(cm/s)	(cm/s)	Diferencia (%)
UN (1)	48.8	-29.9	-	-	-
B (1)	-42.4	39.8	6.4	9.9	55
A (2).	38.6	-25.2	-	-	-
B (2)	-33.4	32.8	5.2	7.6	46
(3)	38.9	-43.1	-	-	-
B (3)	-48.5	36.3	-9.6	-6.8	41

Los resultados de los pasos 2, 3 y 4 confirman las predicciones de la ecuación 3. En el paso 2, el modelo A viene a una parada casi total después de chocar con vela B. Por lo tanto, casi todo su impulso se transfiere al planeador B. En el paso 3, Ala A no viene a una parada después de chocar con la vela mayor B. En su lugar, devuelve en la dirección opuesta después de impartir algún impulso a Ala B. En el paso 4, el ímpetu total del sistema sigue siendo el mismo, a pesar de los cambios de dirección de dos planeadores. El hecho de que, en algunos casos, el ímpetu total parece aumentar y las velocidades de ambos planeadores disminución se relaciona con el hecho de que hay error experimental y las colisiones ellos mismos no son totalmente elásticas. Sonido y el calor que desprenden las colisiones pueden tomar energía del sistema. El hecho de que la pista de aire puede no ser totalmente nivel puede cambiar el comportamiento de las velocidades de los planeadores. Si la pista está un poco inclinada, la velocidad aumentará en esa dirección debido a la gravedad. Todavía, los resultados muestran que el ímpetu total del sistema, independientemente de la velocidad inicial, permanece constante.

Sin conservación del ímpetu, cohetes nunca dejaría la tierra. Cohetes no realmente empujar contra algo-cuentan con empuje a levante. Inicialmente, el combustible de un cohete y el cohete sí mismo son inmóvil y tienen cero ímpetu. Al lanzamiento, el cohete propulsa combustible gastado hacia fuera muy rápidamente. Este combustible tiene masa y momentum. Si el impulso final debe ser igual al impulso inicial (cero) entonces debe ser un impulso en la dirección opuesta del combustible desechado. Así, el cohete se propulsa hacia arriba.

Cualquier persona que nunca ha disparado un arma de fuego comprende la conservación del ímpetu. Como el sistema de combustible del cohete desde arriba, arma/munición también se inicia el sistema en reposo. Cuando la munición de la pistola a una velocidad tremenda, debe ser un impulso en la dirección opuesta para cancelar hacia fuera el impulso de la bala de exceso de velocidad. Esto se conoce como retroceso y pueden ser muy poderosos.

El adorno de escritorio popular que consiste en varias bolas de metal colgando de cuerdas se llama "cuna de Newton" por una buena razón. Es otro ejemplo de la conservación del ímpetu. Cuando una bola se levantó y se suelta, golpea a su vecino, transfiriendo su impulso. El impulso viaja abajo de la línea hasta la última bola tiene el impulso de la primera, haciendo que se mueva hacia afuera. Esto iría para siempre, si no por fuerzas externas, tales como pérdida de la resistencia y la energía del aire debido a las colisiones.

En este experimento, la ley de conservación del ímpetu se verificó al considerar la colisión de dos planeadores en una pista cerca sin fricción. Esta ley fundamental es quizás más importante debido a su poder para resolver problemas. Si alguien sabe los ímpetus iniciales, entonces ella sabe los ímpetus finales y viceversa.