Conservation du mouvement

Source : Nicholas Timmons, Antonella Cooray, Ph.d., département de physique & astronomie, école de Sciences physique, University of California, Irvine, CA

L’objectif de cette expérience est de tester le concept de la conservation de la quantité de mouvement. En mettant en place une surface avec très peu de friction, collisions entre les objets en mouvement peuvent être étudiées, y compris leurs moments initiaux et finaux.

La conservation de la quantité de mouvement est une des lois plus importantes en physique. Quand quelque chose est conservée en physique, la valeur initiale est égale à la valeur finale. Pour le moment, cela signifie que l’élan initial total d’un système sera égale à l’élan final total. Deuxième loi de Newton stipule que la force sur un objet sera égale à la variation dans l’élan de l’objet avec le temps. Ce fait, combiné avec l’idée que le momentum est conservée, sous-tend le fonctionnement de la mécanique classique et est un puissant outil de résolution de problèmes.

Élan est défini comme la masse d’un objet fois sa vitesse :

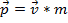. (Équation 1)

On peut aussi définir l’élan en ce qui concerne les forces agissant sur un objet (seconde loi de Newton) :

. (Équation 2)

Ici, 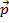est l’élan initial et est l’élan final, avec la même convention utilisée pour temps et . La somme des forces agissant sur un objet est égale à la variation dans l’élan de l’objet avec le temps. Par conséquent, s’il n’y a aucune force nette agissant sur un objet, le changement dans l’élan sera zéro. Dit autrement, dans un système fermé avec aucune force extérieure, l’élan initial sera égale à la quantité de mouvement finale.

Ce concept est plus facilement compréhensible dans le contexte des collisions unidimensionnels et bidimensionnels. Lors d’une collision unidimensionnelle, un objet avec la masse et paraphera vitesse entre en collision avec un autre objet dont la masse et paraphera vitesse 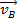. Lors de ces collisions, les forces externes seront assumés pour être trop petit pour avoir un effet. Dans le laboratoire, une voie d’air est utilisée pour réduire la quantité de friction, une force extérieure, sur les planeurs. Si l’élan initial est égal à l’élan final, puis :

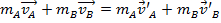, (Équation 3)

où les vitesses apprêtées représentent que les vitesses finales et les vitesses désamorcés représentent les vitesses initiales.

Figure 1 . Montage expérimental.

1. comprendre la minuterie photogate.

1. Utilisation d’une balance, mesurer et noter la masse de chaque aile.
2. Placez un planeur sur la piste avec une seule horloge de photogate.
3. Réglez le minuteur de photogate sur le réglage de la « porte ».
4. Lorsque le planeur traverse le photogate, il enregistrera le temps au cours de laquelle le drapeau au-dessus de l’aile passe à travers la porte. Sur un voyage de retour, la photogate n’affiche pas une nouvelle fois. Interrupteur de la bascule à « lire » afin qu’il affiche le temps initial plus le temps de la seconde passent par la porte.
5. Le drapeau est de 10 cm de long ; déterminer la vitesse du planeur en utilisant le fait que la vitesse est distance divisée par temps.
6. Envoyer l’aile par l’intermédiaire de la photogate plusieurs fois, y compris les allers et retours, après que qu’il a rebondi sur le mur du fond et de mesurer les vitesses afin de se familiariser avec l’équipement. N’oubliez pas que la vitesse a une direction. Laisser la direction de la vitesse initiale représentent positive et la direction opposée qui représentent les valeurs de vitesse négative.

2. deux planeurs de masse égale.

1. Placez les deux planeurs et deux timers de photogate sur la piste, comme dans la Figure 1.
2. Équation 3 permet de déterminer l’expression de la vitesse finale. Dans cette partie de l’expérience, le planeur B partira du reste.
3. Planeur de donner une certaine vitesse initiale afin qu’elle est en collision avec le planeur B. compte rendu la vitesse initiale de planeur A, ainsi que la vitesse finale de chaque aile. Faire cela trois fois, consignez vos résultats et comparez-les à la prédiction théorique.

3. deux planeurs de masse inégal.

1. Ajouter 4 caractères pour planeur B, qui vont doubler sa masse. Répétez les étapes 2.1 à 2.3.

4. égales masses ne pas à partir de repos

1. Retirer les poids de l’aile B.
2. Répétez les étapes 2.1 à 2.3, mais donner le planeur B une vitesse initiale de plus, dans le sens de planeur A.

Le tableau 1. Résultats de deux planeurs de masse égale.

Planeur (version d’essai)	(cm/s)	(cm/s)	(cm/s)	(cm/s)	Différence (%)
UN (1)	72,5	-0,2	-	-	-
B (1)	0.0	67,1	72,5	66.9	8
A (2).	35,6	0,3	-	-	-
B (2)	0.0	37,4	35,6	37,7	6
(3)	47,4	0.0	-	-	-
B (3)	0.0	47,8	47,4	47,8	1

Le tableau 2. Résultats de deux planeurs de masse inégal.

Planeur (version d’essai)	(cm/s)	(cm/s)	(kg cm/s)	(kg cm/s)	Différence (%)
UN (1)	52,9	-10,7	-	-	-
B (1)	0.0	37,7	52,9	64,7	22
A (2).	60.2	-13,2	-	-	-
B (2)	0.0	41,5	60.2	69,8	16
(3)	66,2	-12,0	-	-	-
B (3)	0.0	45,9	66,2	79,7	20

Tableau 3. Résultats de masses égales ne commençant pas du reste.

Planeur (version d’essai)	(cm/s)	(cm/s)	(cm/s)	(cm/s)	Différence (%)
UN (1)	48,8	-29.9	-	-	-
B (1)	-42.4	39,8	6.4	9,9	55
A (2).	38,6	-25.2	-	-	-
B (2)	-33.4	32,8	5.2	7.6	46
(3)	38,9	-43.1	-	-	-
B (3)	-48.5	36,3	-9,6	-6,8	41

Les résultats des étapes 2, 3 et 4 confirment les prédictions faites par l’équation 3. À l’étape 2, le planeur A vient à un arrêt presque complet après une collision avec aile B. Par conséquent, presque tout son élan est transféré au planeur B. À l’étape 3, planeur A ne vient pas à l’arrêt après une collision avec le planeur lourd B. Au contraire, elle retourne dans la direction opposée après avoir donner un élan à l’aile B. À l’étape 4, l’impulsion totale du système reste le même, malgré les changements de direction de deux planeurs. Le fait que, dans certains cas, la quantité de mouvement totale semble s’accroître et les vitesses des deux planeurs diminution est liée au fait qu’il y a des erreurs expérimentales et les collisions elles-mêmes ne sont pas complètement élastiques. Sonore et la chaleur dégagée par les collisions peuvent prendre l’énergie de ce système. Le fait que la voie d’air n’est peut-être pas totalement niveau peut modifier le comportement des vitesses des planeurs. Si la piste est même légèrement inclinée, la vitesse augmentera dans cette direction en raison de la gravité. Les résultats montrent encore que l’impulsion totale du système, indépendamment des vitesses initiales, reste constante.

Sans conservation du moment, fusées ne laisserait jamais le sol. Fusées ne poussent pas réellement sur quoi que ce soit-ils s’appuient sur le sien de décoller. Au départ, le carburant d’une fusée et la fusée elle-même sont immobile et impulsion zéro. Lors du lancement, la fusée propulse de combustible usé à très rapidement. Ce combustible usé a la masse et l’impulsion. Si l’élan final doit être égale à l’élan initial (zéro), puis il doit y avoir un élan dans le sens opposé du carburant mis au rebut. Ainsi, la fusée est propulsée vers le haut.

Quiconque a jamais tiré une arme à feu comprend la conservation de la quantité de mouvement. Comme le système de carburant de fusée / d’en haut, le système d’arme à feu et munitions commence aussi au repos. Lorsque les munitions sont tirée hors de la carabine à une vitesse vertigineuse, il doit y avoir un élan dans le sens inverse pour annuler l’élan de la balle en accélérant. Ceci est connu comme le recul et peuvent être très puissants.

L’ornement populaire Bureau qui est composé de plusieurs boules de métal suspendu à des chaînes est appelée un « berceau de Newton » pour une bonne raison. C’est un autre exemple de la conservation de la quantité de mouvement. Quand une balle est levée et libérée, il frappe son voisin, le transfert de son élan. L’élan se déplace le long de la ligne jusqu'à la dernière balle a l’élan de la première, en faisant pivoter vers l’extérieur. Cela irait à jamais, sinon pour les forces extérieures, comme la perte de résistance et de l’énergie d’air due à des collisions.

Dans cette expérience, la Loi de la conservation du moment a été vérifiée en tenant compte de la collision de deux planeurs sur une piste de près sans frottement. Cette loi fondamentale est peut-être plus important à cause de son pouvoir pour résoudre les problèmes. Si quelqu'un connaît les impulsions initiales, elle sait les impulsions finales et vice versa.