שימור המומנטום

מומנטום מוגדר כמסה של אובייקט כפול המהירות שלו :

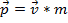. (משוואה 1)

אפשר גם להגדיר מומנטום במונחים של הכוחות הפועלים על אובייקט (החוק השני של ניוטון):

. (משוואה 2)

הנה, 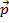הוא המומנטום הראשוני והוא המומנטום הסופי, עם אותה מוסכמה המשמשת לזמן ו . סכום הכוחות הפועלים על אובייקט שווה לשינוי בתנופה של האובייקט עם הזמן. לכן, אם אין כוח נטו הפועל על אובייקט, השינוי בתנופה יהיה אפס. אמר דרך אחרת, במערכת סגורה ללא כוחות חיצוניים, המומנטום הראשוני יהיה שווה למומנטום הסופי.

מושג זה מובן בקלות רבה בהקשר של התנגשויות חד ממדיות ודו-ממדיות. בהתנגשויות חד-ממדיות, עצם עם מסה ומהירות התחלתית מתנגש עם עצם אחר עם מסה ומהירות התחלתית 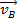. בהתנגשויות אלה, נניח שכוחות חיצוניים קטנים מכדי להשפיע. במעבדה, מסלול אווירי משמש כדי להפחית את כמות החיכוך, כוח חיצוני, על דאונים. אם המומנטום הראשוני שווה למומנטום הסופי, אז:

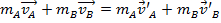(משוואה 3)

כאשר המהירויות המוכנות מייצגות את המהירויות הסופיות והמהירויות הלא-מנוצלות מייצגות את המהירויות ההתחלתיות.

איור 1. התקנה ניסיונית.

טבלה 1. תוצאות של שני דאונים של מסה שווה.

דאון (משפט)	(ס"מ/ש')	(ס"מ/ש')	(ס"מ/ש')	(ס"מ/ש')	הבדל (%)
א' (1)	72.5	-0.2	-	-	-
ב( 1)	0.0	67.1	72.5	66.9	8
א( 2)	35.6	0.3	-	-	-
ב( 2)	0.0	37.4	35.6	37.7	6
א' (3)	47.4	0.0	-	-	-
ב( 3)	0.0	47.8	47.4	47.8	1

טבלה 2. תוצאות משני דאונים של מסה לא שוויונית.

דאון (משפט)	(ס"מ/ש')	(ס"מ/ש')	(ק"ג/ש')	(ק"ג/ש')	הבדל (%)
א' (1)	52.9	-10.7	-	-	-
ב( 1)	0.0	37.7	52.9	64.7	22
א( 2)	60.2	-13.2	-	-	-
ב( 2)	0.0	41.5	60.2	69.8	16
א' (3)	66.2	-12.0	-	-	-
ב( 3)	0.0	45.9	66.2	79.7	20

טבלה 3. תוצאות מגושים שווים שלא מתחילים ממנוחה.

דאון (משפט)	(ס"מ/ש')	(ס"מ/ש')	(ס"מ/ש')	(ס"מ/ש')	הבדל (%)
א' (1)	48.8	-29.9	-	-	-
ב( 1)	-42.4	39.8	6.4	9.9	55
א( 2)	38.6	-25.2	-	-	-
ב( 2)	-33.4	32.8	5.2	7.6	46
א' (3)	38.9	-43.1	-	-	-
ב( 3)	-48.5	36.3	-9.6	-6.8	41

התוצאות עבור שלבים 2, 3 ו- 4 מאשרות את התחזיות של משוואה 3. בשלב 2, דאון A מגיע לעצירה כמעט מוחלטת לאחר התנגשות עם דאון B. לכן, כמעט כל המומנטום שלה מועבר לדאון ב '. בשלב 3, דאון A לא מגיע לעצירה לאחר התנגשות עם דאון כבד B. במקום זאת, הוא חוזר בכיוון ההפוך לאחר שהעניק תנופה כלשהי לדאון B. בשלב 4, התנף הכולל של המערכת נשאר זהה, למרות שינויי הכיוון של שני דאונים. העובדה שבמקרים מסוימים, נראה כי התנום הכולל גדל והמהירויות של שני הדאון פוחתות קשורה לעובדה שיש טעות ניסיונית וההתנגשויות עצמן אינן אלסטיות לחלוטין. קול וחום הנתון על ידי ההתנגשויות יכול לקחת אנרגיה מהמערכת. העובדה שמסלול האוויר לא יכול להיות לגמרי מאוזן יכולה לשנות את ההתנהגות של המהירויות של הדאון. אם המסלול נוטה אפילו מעט, המהירויות יגדלו בכיוון זה עקב כוח המשיכה. התוצאות עדיין מראות כי התנחם הכולל של המערכת, ללא קשר למהירויות ההתחלתיות, נשאר קבוע.

ללא שימור מומנטום, רקטות לעולם לא יעזבו את הקרקע. רקטות לא באמת לדחוף נגד שום דבר - הם מסתמכים על דחף להמריא. בתחילה, הדלק של רקטה והרקטה עצמה הם ללא תנועה ויש להם אפס מומנטום. בעת השיגור, מנועי הרקטות הוציאו דלק במהירות רבה. לדלק המושקע הזה יש מסה ותנופה. אם המומנטום הסופי חייב להיות שווה למומנטום הראשוני (אפס) אז חייב להיות מומנטום בכיוון ההפוך של הדלק שנזרק. לכן, הרקטה נדחף כלפי מעלה.

כל מי שאי פעם ירה באקדח מבין את שימור המומנטום. כמו מערכת הרקטות / דלק מלמעלה, גם מערכת האקדח / התחמושת מתחילה במנוחה. כאשר התחמושת נורתה מהאקדח במהירות עצומה, חייב להיות מומנטום בכיוון ההפוך כדי לבטל את התנע של הכדור במהירות מופרזת. זה ידוע בשם רזון והוא יכול להיות חזק מאוד.

קישוט השולחן הפופולרי המורכב ממספר כדורי מתכת התלויים על חוטים נקרא "עריסת ניוטון" מסיבה טובה. זוהי דוגמה נוספת לשימור המומנטום. כאשר כדור מורם ומשוחרר, הוא מכה את שכנו, ומעביר את המומנטום שלו. המומנטום נע לאורך הקו עד שהכדור האחרון יש את המומנטום של הראשון, גורם לו להתנדנד החוצה. זה יימשך לנצח אלמלא כוחות חיצוניים, כמו התנגדות אווירית ואובדן אנרגיה עקב ההתנגשויות.

בניסוי זה, חוק שימור המומנטום אומת על ידי התחשבות בהתנגשות של שני דאונים במסלול כמעט ללא חיכוך. חוק יסוד זה הוא אולי החשוב ביותר בשל כוחו לפתור בעיות. אם מישהו יודע את הרגעה הראשונית, אז היא יודעת את הרגע האחרון, ולהיפך.