זרימה גלילית צולבת: מדידת התפלגות לחץ והערכת מקדמי גרירה

מקדם הלחץ הלא ממדי, C_p, למיקום שרירותי בתורת הזרימה הפוטנציאלית האידיאלית בכל תנוחה זוויתית, θ, על פני השטח של גליל מעגלי ניתנת על ידי המשוואה הבאה:

מקדם הלחץ C_p מוגדר כ:

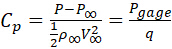
כאשר P הוא הלחץ המוחלט, P_∞ הוא לחץ הזרם החופשי ללא הפרעה, P_gage = P − P_∞ הוא לחץ gage, והוא הלחץ הדינמי, המבוסס על צפיפות הזרם החופשי, ρ_∞, ואת המהירות האווירית, V_∞.

תבנית הזרימה החזויה על ידי תורת הזרימה הפוטנציאלית האידיאלית מוצגת באיור 1. הזרימה היא סימטרית, ולכן יש אפס כוח גרירה נטו. זה נקרא הפרדוקס של ד'אלמבר [1].

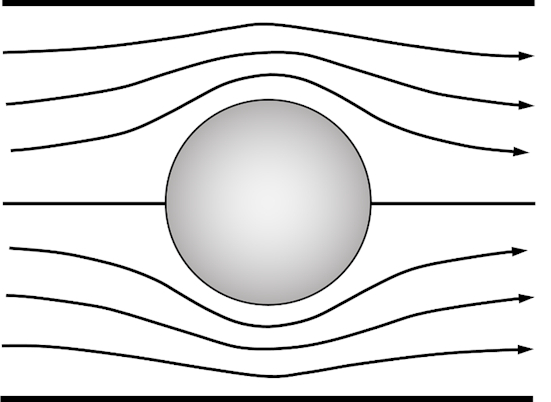
איור 1. תבנית זרימה של זרימה חוצת גליליות אידיאלית במנהרת רוח.

עם זאת, כוח גרירה אפס נטו אינו צפוי בתנאי זרימה אמיתיים. כוח הגרירה של צילינדר, F_D, לכל אורך יחידה של הגליל עקב הבדלי לחץ ניתן על ידי:

האינטגרציה נלקחת לאורך היקף הגליל.

בניסוי זה, מדידות לחץ gage נאספים מ 24 יציאות לחץ לאורך הגליל. לאחר מכן, ניתן להעריך את המשוואה לעיל באופן מספרי באמצעות לחץ gage הנמדד כדלקמן:

כאשר P_gagei הוא לחץ gage במיקום של θ_i, θ_i הוא המיקום הזוויתי, r הוא הרדיוס של הגליל, ו 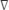θ הוא המרחק הזוויתי בין יציאות סמוכות, שהוא 15 °. לחץ הגייג' נקבע באמצעות לוח מנורה מבטאים עם 24 עמודות עצמאיות, לחץ הגייג' נקבע באמצעות המשוואה הבאה:

כאשר Δh הוא הפרש הגובה של המנומטר בהתייחס ללחץ הזרם החופשי, ρ_L הוא צפיפות הנוזל במנומטר, ו- g הוא התאוצה עקב כוח המשיכה. לאחר קבלת כוח הגרירה, ניתן לקבוע את מקדם הגרירה הלא ממדי C_D באמצעות:

כאשר d = 2r הוא הקוטר של הגליל.

כזכור הפרדוקס של ד'אלמבר, כוח הגרירה נובע מההשפעות המוזנחות של צמיגות. ראשית, שכבת גבול מתפתחת לאורך הגליל כתוצאה מכוחות צמיגים. כוחות צמיגים אלה גורמים לגרירת חיכוך עור. שנית, הגליל הוא אובייקט בלוף (לא יעיל). זה יוצר הפרדת זרימה והתעוררות בלחץ נמוך מאחוריו וגורם לכוח גרירה גדול יותר בשל הפרש הלחץ. איור 2 מציג מספר דפוסי זרימה אופייניים שנצפים באופן ניסיוני. דפוסי זרימה אמיתיים מסתמכים על מספר ריינולדס, Re, המוגדר כ:

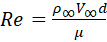
כאשר הפרמטר μ הוא הצמיגות הדינמית של הנוזל.

איור 2. סוגים שונים של דפוסי זרימה מעל גליל.

תוצאות ניסוי עבור צילינדר נקי ומופרע מוצגים שולחנות 1 ו 2, בהתאמה. ניתן להתוות את הנתונים בגרף של מקדם הלחץ C_p, לעומת מיקום זוויתי, θ, לזרימה אידיאלית ואמיתית כפי שמוצג באיור 6.

יציאת לחץ #	זווית מיקום q (°)	Pgage מקריאות מנורמטר (ב. מים)	מקדם לחץ מחושב Cp
0	0	1.7	1.00
1	15	1.4	0.83
2	30	0.0	0.01
3	45	-1.7	-0.98
4	60	-2.7	-1.57
5	75	-3.7	-2.15
6	90	-3.3	-1.92
7	105	-3.0	-1.74
8	120	-3.2	-1.86
9	135	-3.2	-1.86
10	150	-3.3	-1.92
11	165	-3.5	-2.03
12	180	-3.4	-1.97

טבלה 1. תוצאות ניסוי לצילינדר הנקי. בשל סימטריה, מוצגים רק נתונים עבור יציאות מספר 0-12.

יציאת לחץ #	זווית מיקום q (°)	Pgage מקריאות מנורמטר (ב. מים)	מקדם לחץ מחושב Cp
0	0	1.8	1.05
1	15	1.6	0.93
2	30	0.6	0.35
3	45	-1.3	-0.73
4	60	-2.9	-1.69
5	75	-4.0	-2.31
6	90	-4.0	-2.33
7	105	-1.7	-0.99
8	120	-1.5	-0.89
9	135	-1.4	-0.84
10	150	-1.4	-0.84
11	165	-1.5	-0.87
12	180	-1.4	-0.84

טבלה 2. תוצאות ניסוי לצילינדר המופרע. בשל סימטריה, מוצגים רק נתונים עבור יציאות מספר 0-12.

איור 6. התפלגות מקדם לחץ, C_p, לעומת מיקום זוויתי, θ, בין זרימה אידיאלית לזרימה אמיתית.

בנקודת הקיפאון, θ = 0°, C_p מגיע לערך המרבי של C_p = 1. עבור θ < 60°, התפלגות מקדם הלחץ דומה עבור כל שלוש העקומות. כאן זרימת שכבת הגבול למינארית מחוברת לפני השטח של הגליל. עבור θ > 60°, שני דפוסי הזרימה הניסיוניים לסטות מן הזרימה האידיאלית; הם יוצרים אזור בלחץ נמוך בחלק האחורי של הגליל, אשר מלא מערבולות סוערות אדי. זהו אזור ההשכה שנקרא. זה הפרש הלחץ בין הקדמי לחלק האחורי של הגליל שגורם גרירה גדולה כי הוא ציין בזרימה גלילית צולבת.

למרות הדמיון בדפוסי הזרימה בין הגליל הנקי לצילינדר מופרע, יש גם הבדלים. הזרימה המופרעת נוטה לעטוף את הגליל יותר לפני הפרדת הזרימה, ויש לה גם לחץ גב גבוה יותר. פעולה זו גורמת פחות גרירה, אשר מאומת על-ידי חישובי גרירה. זה קורה כי זרימת למינאר בחלק הקדמי של הגליל יש נטייה לזרום ישר וקשה עבור הזרימה לעטוף סביב הגליל. עבור הגליל המופרע, הזרימה מיד עוברת לזרימה סוערת ובכך יכולה לעטוף סביב הגליל יותר מאשר הצילינדר הנקי.

תצורות זרימה	גרור מקדם, CD
1. גליל נקי	1.68
2. צילינדר מופרע	0.78

טבלה 4. גרור מקדם, C_D (מספר ריינולדס Re = 1.78 x 10⁵).

מקדם הגרירה C_D לצילינדר נקי במהירות אווירית של 60 קמ"ש או Re = 178,000 הוערך באופן ניסיוני והוא בערך 1.5 [2], שהוא קרוב לערך של 1.68 שהושג בניסוי זה עבור צילינדר נקי.

מתוצאות ניסוי קודמות [2], מקדם הגרירה C_D יורד ב- Re = 3 x 10⁵. הסיבה לכך היא שהמעבר מזרימה למינארית לזרימה סוערת מתרחש באופן טבעי אפילו עם צילינדר חלק. בניסוי, מעבר הזרימה הסוער נצפה פשוט על ידי הדבקת מחרוזת בקוטר 1 מ"מ לפני השטח של הגליל. לכן, מקדם גרירה נמוך יותר C_D של 0.78 בלבד מתקבל עבור הצילינדר המופרע.

זרימה גלילית צולבת נחקרה באופן תיאורטי וניסיוני מאז המאה ה -18. מציאת הפערים בין השניים מאפשרת לנו להרחיב את הבנתנו את דינמיקת הנוזלים ולחקור מתודולוגיות חדשות. תורת זרימת שכבת הגבול פותחה על ידי פראנדל [3] בתחילת המאה ה-20, והיא דוגמה טובה להרחבת הזרימה העיקשת לתורת הזרימה הקרבית בפתרון הפרדוקס של ד'אלמבר.

בניסוי זה, הזרימה הגלילית הצולבת נחקרה במנהרת רוח ו-24 יציאות של מדידת לחץ נעשו כדי למצוא את התפלגות הלחץ לאורך פני השטח של הגליל. מקדם הגרירה חושב והוא מסכים היטב עם מקורות אחרים. המניפולציה של הזרימה כדי לעורר זרימת גבול סוערת במספר ריינולדס נמוך יחסית הודגמה גם.