Flujo cilíndrico transversal: medición de la distribución de la presión y estimación de los coeficientes de arrastre
Visión general
Fuente: David Guo, College of Engineering, Technology, and Aeronautics (CETA), Southern New Hampshire University (SNHU), Manchester, New Hampshire
Las distribuciones de presión y las estimaciones de arrastre para el flujo cilíndrico cruzado se han investigado durante siglos. Mediante la teoría de flujo potencial inviscida ideal, la distribución de la presión alrededor de un cilindro es verticalmente simétrica. La distribución de presión aguas arriba y aguas abajo del cilindro también es simétrica, lo que resulta en una fuerza de arrastre de red cero. Sin embargo, los resultados experimentales producen patrones de flujo, distribuciones de presión y coeficientes de arrastre muy diferentes. Esto se debe a que la teoría potencial inviscida ideal asume el flujo irrotacional, lo que significa que la viscosidad no se considera ni se tiene en cuenta al determinar el patrón de flujo. Esto difiere significativamente de la realidad.
En esta demostración, se utiliza un túnel de viento para generar una velocidad de aire especificada, y se utiliza un cilindro con 24 puertos de presión para recopilar datos de distribución de presión. Esta demostración ilustra cómo la presión de un fluido real que fluye alrededor de un cilindro circular difiere de los resultados predichos en función del flujo potencial de un fluido idealizado. El coeficiente de arrastre también se estimará y se comparará con el valor predicho.
Principios
El coeficiente de presión no dimensional, Cp, para una posición arbitraria en la teoría de flujo potencial ideal en cualquier posición angular, s, en la superficie de un cilindro circular se da por la siguiente ecuación:

El coeficiente de presión Cp se define como:
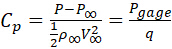
donde P es la presión absoluta, Pes la presión de flujo libre no perturbada,  el medidor P a P es la presión del medidor, y es la presión dinámica, que se basa en la densidad de la corriente libre, ,y la velocidad del aire, V.
el medidor P a P es la presión del medidor, y es la presión dinámica, que se basa en la densidad de la corriente libre, ,y la velocidad del aire, V.
El patrón de flujo predicho por la teoría de flujo potencial ideal se muestra en la Figura 1. El flujo es simétrico y, por lo tanto, no hay fuerza de arrastre neta cero. Esto se llama Paradoja de D'Alembert [1].
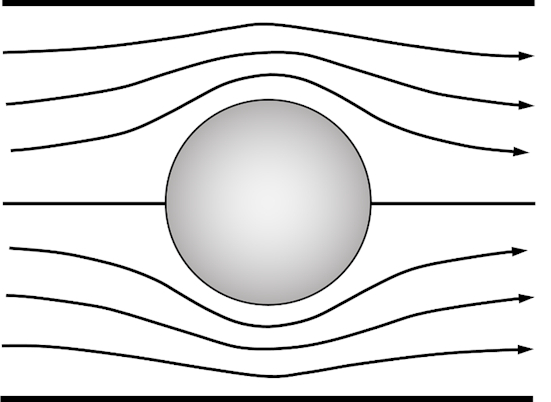
Figura 1. Patrón de flujo de un flujo intercilíndrico ideal en un túnel de viento.
Sin embargo, no se espera una fuerza de arrastre cero neto en condiciones de flujo reales. La fuerza de arrastre de un cilindro, FD, por unidad de longitud del cilindro debido a las diferencias de presión se da por:

La integración se lleva a lo largo del perímetro del cilindro.
En este experimento, las mediciones de presión del medidor se recogen de 24 puertos de presión a lo largo del cilindro. A continuación, la ecuación anterior se puede evaluar numéricamente utilizando la presión del medidor medida de la siguiente manera:

donde El medidor Pi es la presión del medidor en la ubicación de i , i es la posición angular, r es el radio del cilindro, y 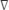 es la distancia angular entre adyacente puertos, que es de 15o. La presión del medidor se determina mediante un panel manómetro con 24 columnas independientes, la presión del medidor se determina utilizando la siguiente ecuación:
es la distancia angular entre adyacente puertos, que es de 15o. La presión del medidor se determina mediante un panel manómetro con 24 columnas independientes, la presión del medidor se determina utilizando la siguiente ecuación:

dondeh es la diferencia de altura del manómetro en referencia a la presión de flujo libre, L es la densidad del líquido en el manómetro, y g es la aceleración debido a la gravedad. Una vez obtenida la fuerza de arrastre, el coeficiente de arrastre no dimensional CD se puede determinar a través de:

donde d á 2r es el diámetro del cilindro.
Recordando la Paradoja de D'Alembert, la fuerza de arrastre se debe a los efectos descuidados de la viscosidad. En primer lugar, una capa límite se desarrolla a lo largo del cilindro como resultado de fuerzas viscosas. Estas fuerzas viscosas causan resistencia a la fricción de la piel. En segundo lugar, el cilindro es un objeto de farol (no aerodinámico). Esto crea separación de flujo y una estela de baja presión detrás de él y causa una fuerza de arrastre más grande debido al diferencial de presión. La Figura 2 muestra varios patrones de flujo típicos que se observan experimentalmente. Los patrones de flujo reales se basan en el número de Reynolds, Re, que se define como:
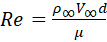
donde el parámetro es la viscosidad dinámica del fluido.

Figura 2. Varios tipos de patrones de flujo sobre un cilindro.
Procedimiento
1. Medición de la distribución de la presión alrededor de un cilindro
- Retire la cubierta superior de la sección de prueba de un túnel de viento y monte un cilindro de aluminio limpio (d 4 pulg.) con 24 puertos incorporados en un plato giratorio(Figura 3). Instale el cilindro de modo que el puerto cero esté orientado aguas arriba(Figura 4a).
- Vuelva a colocar la cubierta superior y conecte los 24 tubos de presión etiquetados 0 - 23 a los puertos correspondientes en el panel del manómetro. El panel del manómetro debe llenarse con aceite de color pero marcado en el agua en graduaciones (Figura 5).
- Encienda el túnel de viento y corra a 60 mph. Registre las 24 mediciones de presión leyendo el manómetro. A esta velocidad, el número de Reynolds es 1.78 x 105. El patrón de flujo esperado se muestra en la Figura 2d.
- Una vez grabadas todas las mediciones, apague el túnel de viento y tape dos cuerdas (d x 1 mm) verticalmente en el cilindro para crear el cilindro perturbado. Tape una cadena entre los puertos 3 y 4 (a 52,5o) y la otra entre los puertos 20 y 21 (a 307,5o). Asegúrese de que los puertos cercanos no estén bloqueados por la cinta, como se muestra en la figura 4b.
- Encienda el túnel de viento y repita el paso 3. Registre todas las mediciones de presión.

Figura 3. Disposición de medición de presión de medición de medición de flujo cilíndrico cruzado.

Figura 4. Configuración del cilindro en el túnel de viento (los puertos de presión están en el centro del cilindro).

Figura 5. Panel del manómetro.
Resultados
Los resultados experimentales del cilindro limpio y perturbado se muestran en las Tablas 1 y 2,respectivamente. Los datos se pueden trazar en un gráfico del coeficiente de presión, Cp, frente a la posición angular, para un flujo ideal y real como se muestra en la Figura 6.
| Puerto de presión # | Angulo de posición q (o) | Pmedidor de lecturas del manómetro (in. agua) | Coeficiente de presión calculado Cp |
| 0 | 0 | 1.7 | 1.00 |
| 1 | 15 | 1.4 | 0.83 |
| 2 | 30 | 0.0 | 0.01 |
| 3 | 45 | -1.7 | -0.98 |
| 4 | 60 | -2.7 | -1.57 |
| 5 | 75 | -3.7 | -2.15 |
| 6 | 90 | -3.3 | -1.92 |
| 7 | 105 | -3.0 | -1.74 |
| 8 | 120 | -3.2 | -1.86 |
| 9 | 135 | -3.2 | -1.86 |
| 10 | 150 | -3.3 | -1.92 |
| 11 | 165 | -3.5 | -2.03 |
| 12 | 180 | -3.4 | -1.97 |
Tabla 1. Resultados experimentales para el cilindro limpio. Debido a la simetría, solo se muestran los datos de los puertos del número 0-12.
| Puerto de presión # | Angulo de posición q (o) | Pmedidor de lecturas del manómetro (in. agua) | Coeficiente de presión calculado Cp |
| 0 | 0 | 1.8 | 1.05 |
| 1 | 15 | 1.6 | 0.93 |
| 2 | 30 | 0.6 | 0.35 |
| 3 | 45 | -1.3 | -0.73 |
| 4 | 60 | -2.9 | -1.69 |
| 5 | 75 | -4.0 | -2.31 |
| 6 | 90 | -4.0 | -2.33 |
| 7 | 105 | -1.7 | -0.99 |
| 8 | 120 | -1.5 | -0.89 |
| 9 | 135 | -1.4 | -0.84 |
| 10 | 150 | -1.4 | -0.84 |
| 11 | 165 | -1.5 | -0.87 |
| 12 | 180 | -1.4 | -0.84 |
Cuadro 2. Resultados experimentales para el cilindro perturbado. Debido a la simetría, solo se muestran los datos de los puertos del número 0-12.

Figura 6. Distribución del coeficiente de presión, Cp, vs posición angular, o, entre el flujo ideal y real.
En el punto de estancamiento, a 0o, Cp alcanza su valor máximo de Cp a 1. Para el grado de < 60o, la distribución del coeficiente de presión es similar para las tres curvas. Aquí es donde el flujo de capa límite laminar se une a la superficie del cilindro. Para el valor de > 60o, los dos patrones de flujo experimentales se desvían del flujo ideal; forman una región de baja presión en la parte posterior del cilindro, que está llena de vórtices y remolinos turbulentos. Esta es la región llamada wake. Es la diferencia de presión entre la parte delantera y la parte posterior del cilindro lo que provoca el gran arrastre que se observa en el flujo cilíndrico cruzado.
A pesar de la similitud en los patrones de flujo entre el cilindro limpio y el cilindro perturbado, también hay diferencias. El flujo perturbado tiende a envolver alrededor del cilindro más antes de la separación del flujo, y también tiene una mayor contrapresión. Esto provoca menos arrastre, que se verifica mediante los cálculos de arrastre. Esto ocurre porque el flujo laminar en la parte delantera del cilindro tiene una tendencia a fluir recto y es difícil para el flujo envolver alrededor del cilindro. Para el cilindro perturbado, el flujo pasa inmediatamente en flujo turbulento y por lo tanto puede envolver alrededor del cilindro más que el cilindro limpio.
| Configuraciones de flujo | Coeficiente de arrastre, CD |
| 1. Limpie el cilindro | 1.68 |
| 2. Cilindro perturbado | 0.78 |
Cuadro 4. Coeficiente de arrastre, CD (número de Reynolds Re á 1,78 x 105).
El coeficiente de arrastre CD para cilindros limpios a 60 mph de velocidad de aire o Re a 178.000 ha sido evaluado experimentalmente y es de aproximadamente 1,5 [2], que es cercano al valor de 1,68 que se obtuvo en este experimento para un cilindro limpio.
A partir de los resultados experimentales anteriores [2], el coeficiente de arrastre CD cae en Re 3 x 105. Esto se debe a que la transición del flujo laminar al flujo turbulento se produce naturalmente incluso con un cilindro liso. En el experimento, la transición del flujo turbulento se observa simplemente pegando una cuerda de 1 mm de diámetro a la superficie del cilindro. Por lo tanto, se obtiene un coeficiente de arrastre CD inferior de sólo 0,78 para el cilindro perturbado.
Aplicación y resumen
El flujo cilíndrico cruzado se ha investigado teórica y experimentalmente desde el siglo XVIII. Encontrar las discrepancias entre los dos nos permite ampliar nuestra comprensión de la dinámica de fluidos y explorar nuevas metodologías. La teoría del flujo de capa límite fue desarrollada por Prandtl [3] a principios del siglo XX, y es un buen ejemplo de la extensión del flujo invinfectado a la teoría del flujo viscid en la resolución de la Paradoja de D'Alembert.
En este experimento, el flujo cilíndrico transversal se investigó en un túnel de viento y se hicieron los 24 puertos de medición de presión para encontrar la distribución de presión a lo largo de la superficie del cilindro. El coeficiente de arrastre se calculó y está bien de acuerdo con otras fuentes. También se demostró la manipulación del flujo para desencadenar un flujo límite turbulento en un número de Reynolds muy bajo.
Referencias
- d'Alembert, Jean le Rond (1752), Essai d'une nouvelle théorie de la résistance des fluides
- John D. Anderson (2017), Fundamentals of Aerodynamics, 6th Edition, ISBN: 978-1-259-12991-9, McGraw-Hill
- Prandtl, Ludwig (1904), Motion of fluids with very little viscosity, 452, NACA Technical Memorandum
Saltar a...
Vídeos de esta colección:

Now Playing
Flujo cilíndrico transversal: medición de la distribución de la presión y estimación de los coeficientes de arrastre
Aeronautical Engineering
16.1K Vistas

Rendimiento aerodinámico en un modelo de avión: El DC-6B
Aeronautical Engineering
8.3K Vistas

Caracterización de la hélice: Variaciones en el paso, el diámetro y el número de palas en el rendimiento
Aeronautical Engineering
26.2K Vistas

Comportamiento de la superficie aerodinámica: Distribución de la presión en un ala Clark Y-14
Aeronautical Engineering
21.0K Vistas

Rendimiento del ala Clark Y-14: Despliegue de dispositivos de elevación alta (Flaps y Slats)
Aeronautical Engineering
13.3K Vistas

Método esfera de turbulencia: Evaluación de la calidad del flujo del túnel de viento
Aeronautical Engineering
8.7K Vistas

Análisis de boquillas: variaciones en el número de Mach y la presión a lo largo de una boquilla convergente y una convergente-divergente
Aeronautical Engineering
37.9K Vistas

Fotografías de Schlieren: Una técnica para visualizar las características del flujo supersónico
Aeronautical Engineering
11.4K Vistas

Visualización del flujo en un túnel de agua: Observación del vórtice en el borde de ataque sobre un ala Delta
Aeronautical Engineering
8.0K Vistas

Visualización del flujo de tinte superficial: Un método cualitativo para observar los patrones de las líneas del tramo en un flujo supersónico
Aeronautical Engineering
4.9K Vistas

Tubo Pitot-estático: Un dispositivo para medir la velocidad del flujo de aire
Aeronautical Engineering
48.7K Vistas

Anemometría de temperatura constante:Uuna herramienta para estudiar el flujo de capa de límite turbulenta
Aeronautical Engineering
7.2K Vistas

Transductor de presión: Calibración mediante un tubo de Pitot estático
Aeronautical Engineering
8.5K Vistas

Control de vuelo en tiempo real: calibración de sensores integrados y adquisición de datos
Aeronautical Engineering
10.2K Vistas

Aerodinámica de multicópteros: Caracterización del empuje en un hexacóptero
Aeronautical Engineering
9.1K Vistas
ACERCA DE JoVE
Copyright © 2025 MyJoVE Corporation. Todos los derechos reservados