Querzylindrische Strömung: Messung der Druckverteilung und Einschätzung des Strömungswiderstandskoeffizient
Überblick
Quelle: David Guo, College of Engineering, Technology, and Aeronautics (CETA), Southern New Hampshire University (SNHU), Manchester, New Hampshire
Die Druckverteilungen und Zugabschätzungen für den kreuzzylindrischen Fluss werden seit Jahrhunderten untersucht. Durch die ideale inviszide Potentialflusstheorie ist die Druckverteilung um einen Zylinder vertikal symmetrisch. Die Druckverteilung vor und nach dem Zylinder ist ebenfalls symmetrisch, was zu einer Null-Netto-Luftwiderstandskraft führt. Experimentelle Ergebnisse liefern jedoch sehr unterschiedliche Strömungsmuster, Druckverteilungen und Luftwiderstandskoeffizienten. Dies liegt daran, dass die ideale inviszide Potentialtheorie einen irrotationalen Fluss voraussetzt, was bedeutet, dass die Viskosität bei der Bestimmung des Strömungsmusters nicht berücksichtigt oder berücksichtigt wird. Das unterscheidet sich deutlich von der Realität.
In dieser Demonstration wird ein Windkanal verwendet, um eine bestimmte Fluggeschwindigkeit zu erzeugen, und ein Zylinder mit 24 Druckanschlüssen wird verwendet, um Druckverteilungsdaten zu sammeln. Diese Demonstration zeigt, wie sich der Druck einer realen Flüssigkeit, die um einen Kreisförmigen Zylinder fließt, von den vorhergesagten Ergebnissen unterscheidet, basierend auf dem potenziellen Fluss einer idealisierten Flüssigkeit. Der Luftwiderstandskoeffizient wird ebenfalls geschätzt und mit dem vorhergesagten Wert verglichen.
Grundsätze
Der nichtdimensionale Druckkoeffizient Cpfür eine beliebige Position in idealer Potentialflusstheorie an jeder Winkelposition, , auf der Oberfläche eines kreisförmigen Zylinders wird durch die folgende Gleichung angegeben:

Der Druckkoeffizient Cp ist definiert als:
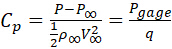
wobei P der absolute Druck ist, P- der ungestörte Freistromdruck, Pgage = P - P- der Gagedruck ist, und  ist der dynamische Druck, der auf der Freistromdichte basiert, -und Fluggeschwindigkeit, V.
ist der dynamische Druck, der auf der Freistromdichte basiert, -und Fluggeschwindigkeit, V.
Das durch die ideale Potentialflusstheorie vorhergesagte Strömungsmuster ist in Abbildung 1dargestellt. Der Durchfluss ist symmetrisch, und daher gibt es null Netto-Drag-Force. Dies wird D'Alemberts Paradox [1] genannt.
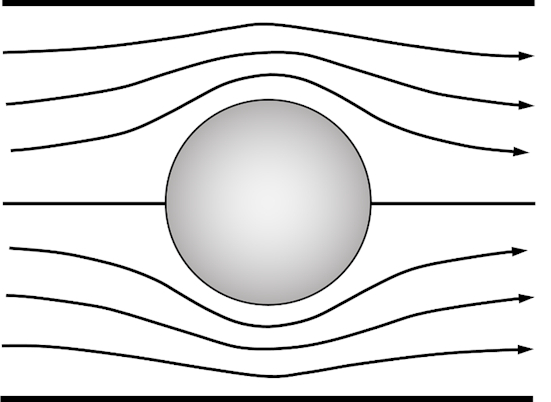
Abbildung 1. Strömungsmuster eines idealen querzylindrischen Durchflusses in einem Windkanal.
Eine Netto-Null-Drag-Force ist jedoch unter realen Strömungsbedingungen nicht zu erwarten. Die Durchzugskraft eines Zylinders, FD, pro Längeneinheit des Zylinders aufgrund von Druckunterschieden wird angegeben durch:

Die Integration erfolgt entlang des Zylinderumfangs.
In diesem Experiment werden Messdruckmessungen aus 24 Druckanschlüssen entlang des Zylinders gesammelt. Dann kann die obige Gleichung mit dem gemessenen Messdruck wie folgt numerisch ausgewertet werden:

wobei Pgagei der Gage-Druck an der Stelle von i ist, i die Winkelposition, r der Radius des Zylinders und  der Winkelabstand zwischen benachbarten 15°. Der Messdruck wird mit einem Manometer-Panel mit 24 unabhängigen Säulen bestimmt, der Messdruck wird mit der folgenden Gleichung bestimmt:
der Winkelabstand zwischen benachbarten 15°. Der Messdruck wird mit einem Manometer-Panel mit 24 unabhängigen Säulen bestimmt, der Messdruck wird mit der folgenden Gleichung bestimmt:

wobei der Höhenunterschied des Manometers in Bezug auf den Freistromdruck ,,L" die Dichte der Flüssigkeit im Manometer und g die Beschleunigung aufgrund der Schwerkraft ist. Sobald die Zugkraft erreicht ist, kann der nicht dimensionale Ziehkoeffizient CD bestimmt werden durch:

wobei d = 2r der Zylinderdurchmesser ist.
Erinnert an D'Alemberts Paradoxon, ist die Zugkraft auf die vernachlässigten Auswirkungen der Viskosität zurückzuführen. Zunächst entwickelt sich entlang des Zylinders eine Grenzschicht als Folge von viskosen Kräften. Diese zähflüssigen Kräfte verursachen Hautreibungswiderstand. Zweitens ist der Zylinder ein Bluff-Objekt (nicht stromlinienförmig). Dies erzeugt eine Strömungstrennung und einen Niederdruckwecker dahinter und verursacht durch die Druckdifferenz eine größere Zugkraft. Abbildung 2 zeigt mehrere typische Strömungsmuster, die experimentell beobachtet werden. Reale Flussmuster basieren auf der Reynolds-Nummer Re, die wie folgt definiert ist:
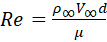
wobei der Parameter n die dynamische Viskosität der Flüssigkeit ist.

Abbildung 2. Verschiedene Arten von Strömungsmustern über einem Zylinder.
Verfahren
1. Messung der Druckverteilung um einen Zylinder
- Entfernen Sie die obere Abdeckung des Prüfabschnitts eines Windkanals, und montieren Sie einen sauberen Aluminiumzylinder (d = 4 in) mit 24 eingebauten Anschlüssen an einem Drehteller (Abbildung 3). Installieren Sie den Zylinder so, dass Port Zero vorgelagert ist (Abbildung 4a).
- Ersetzen Sie die obere Abdeckung, und schließen Sie die 24 Druckrohre mit der Bezeichnung 0 - 23 an die entsprechenden Anschlüsse auf dem Manometerpanel an. Das Manometer-Panel sollte mit farbigem Öl gefüllt werden, aber in Wasser in markiert werden. Graduierungen (Abbildung 5).
- Schalten Sie den Windkanal ein und führen Sie ihn mit 60 mph. Zeichnen Sie alle 24 Druckmessungen auf, indem Sie das Manometer lesen. Bei dieser Fluggeschwindigkeit ist die Reynolds-Zahl 1,78 x 105. Das erwartete Strömungsmuster ist in Abbildung 2ddargestellt.
- Sobald alle Messungen aufgezeichnet wurden, schalten Sie den Windkanal aus und banden zwei Saiten (d = 1 mm) vertikal auf den Zylinder, um den gestörten Zylinder zu erzeugen. Band eine Schnur zwischen den Ports 3 und 4 (- = 52,5°) und die andere zwischen den Ports 20 und 21 (s = 307,5°). Stellen Sie sicher, dass die Ports in der Nähe nicht durch das Band blockiert sind, wie in Abbildung 4bgezeigt.
- Schalten Sie den Windkanal ein, und wiederholen Sie Schritt 3. Zeichnen Sie alle Druckmessungen auf.

Abbildung 3. Gage-Druckmesslayout des querzylindrischen Durchflusses.

Abbildung 4. Aufbau des Zylinders im Windkanal (Druckanschlüsse befinden sich in der Mitte des Zylinders).

Abbildung 5. Manometer-Panel.
Ergebnisse
Die Experimentellen Ergebnisse für den sauberen und gestörten Zylinder sind in den Tabellen 1 bzw. 2dargestellt. Die Daten können in einem Diagramm des Druckkoeffizienten Cpim Vergleich zur Winkelstellung, b, für einen idealen und realen Durchfluss dargestellt werden, wie in Abbildung 6dargestellt.
| Druckanschluss # | Positionswinkel q (°) | Pgage aus Manometer-Messungen (in Wasser) | Berechneter Druckkoeffizient Cp |
| 0 | 0 | 1.7 | 1.00 |
| 1 | 15 | 1.4 | 0.83 |
| 2 | 30 | 0.0 | 0.01 |
| 3 | 45 | -1.7 | -0.98 |
| 4 | 60 | -2.7 | -1.57 |
| 5 | 75 | -3.7 | -2.15 |
| 6 | 90 | -3.3 | -1.92 |
| 7 | 105 | -3.0 | -1.74 |
| 8 | 120 | -3.2 | -1.86 |
| 9 | 135 | -3.2 | -1.86 |
| 10 | 150 | -3.3 | -1.92 |
| 11 | 165 | -3.5 | -2.03 |
| 12 | 180 | -3.4 | -1.97 |
Tabelle 1. Experimentelle Ergebnisse für den sauberen Zylinder. Aufgrund der Symmetrie werden nur Daten für die Ports Nummer 0-12 angezeigt.
| Druckanschluss # | Positionswinkel q (°) | Pgage aus Manometer-Messungen (in Wasser) | Berechneter Druckkoeffizient Cp |
| 0 | 0 | 1.8 | 1.05 |
| 1 | 15 | 1.6 | 0.93 |
| 2 | 30 | 0.6 | 0.35 |
| 3 | 45 | -1.3 | -0.73 |
| 4 | 60 | -2.9 | -1.69 |
| 5 | 75 | -4.0 | -2.31 |
| 6 | 90 | -4.0 | -2.33 |
| 7 | 105 | -1.7 | -0.99 |
| 8 | 120 | -1.5 | -0.89 |
| 9 | 135 | -1.4 | -0.84 |
| 10 | 150 | -1.4 | -0.84 |
| 11 | 165 | -1.5 | -0.87 |
| 12 | 180 | -1.4 | -0.84 |
Tabelle 2. Experimentelle Ergebnisse für den gestörten Zylinder. Aufgrund der Symmetrie werden nur Daten für die Ports Nummer 0-12 angezeigt.

Abbildung 6. Druckkoeffizientenverteilung, Cp,Vs Winkelposition, b, zwischen idealem und realem Durchfluss.
An der Stagnationsstelle , n = 0°, erreicht Cp seinen Maximalwert von Cp = 1. Bei < 60° ist die Druckkoeffizientenverteilung für alle drei Kurven ähnlich. Hier wird der laminare Grenzschichtfluss an der Zylinderoberfläche befestigt. Bei einem Wert von > 60° weichen die beiden experimentellen Strömungsmuster vom idealen Durchfluss ab; sie bilden einen Niederdruckbereich im hinteren Teil des Zylinders, der mit turbulenten Wirbeln und Wirbeln gefüllt ist. Dies ist die so genannte Wake-Region. Es ist der Druckunterschied zwischen der Vorder- und Rückseite des Zylinders, der den großen Luftwiderstand verursacht, der bei der querzylindrischen Strömung beobachtet wird.
Trotz der Ähnlichkeit der Strömungsmuster zwischen dem sauberen Zylinder und dem gestörten Zylinder gibt es auch Unterschiede. Der gestörte Durchfluss neigt dazu, den Zylinder vor der Strömungstrennung mehr umzuwickeln, und er hat auch einen höheren Gegendruck. Dies führt zu weniger Luftwiderstand, der durch die Ziehberechnungen überprüft wird. Dies geschieht, weil der laminare Fluss in der Vorderseite des Zylinders eine Tendenz hat, gerade zu fließen und es für den Durchfluss schwierig ist, sich um den Zylinder zu wickeln. Für den gestörten Zylinder übergeht der Durchfluss sofort in einen turbulenten Durchfluss und kann so mehr um den Zylinder wickeln als der saubere Zylinder.
| Flow-Konfigurationen | Ziehkoeffizient, CD |
| 1. Sauberer Zylinder | 1.68 |
| 2. Gestörter Zylinder | 0.78 |
Tabelle 4. Luftwiderstandskoeffizient, CD (Reynoldszahl Re = 1,78 x 105).
Der Luftwiderstandskoeffizient CD für einen sauberen Zylinder mit einer Fluggeschwindigkeit von 60 mph oder Re = 178.000 wurde experimentell ausgewertet und liegt bei etwa 1,5 [2], was in der Nähe des Wertes von 1,68 liegt, der in diesem Experiment für einen sauberen Zylinder ermittelt wurde.
Aus früheren Experimentellen Ergebnissen [2] fällt der Luftwiderstandskoeffizient CD bei Re = 3 x 105. Denn der Übergang vom laminaren Fluss zum turbulenten Fluss erfolgt natürlich auch bei einem glatten Zylinder. Im Experiment wird der turbulente Strömungsübergang durch einfaches Kleben einer 1-mm-Durchmesserschnur an der Zylinderoberfläche beobachtet. Somit wird für den gestörten Zylinder ein niedrigerer Luftwiderstandskoeffizient CD von nur 0,78 ermittelt.
Anwendung und Zusammenfassung
Der kreuzzylindrische Fluss wird seit dem 18. Jahrhundert theoretisch und experimentell untersucht. Die Diskrepanzen zwischen den beiden zu finden, ermöglicht es uns, unser Verständnis der Strömungsdynamik zu erweitern und neue Methoden zu erforschen. Die Theorie des Grenzschichtflusses wurde von Prandtl [3] Anfang des 20. Jahrhunderts entwickelt und ist ein gutes Beispiel für die Ausdehnung des invisziden Flusses auf die viszide Strömungstheorie bei der Lösung von D'Alemberts Paradoxon.
In diesem Experiment wurde der kreuzzylindrische Fluss in einem Windkanal untersucht und die 24 Druckmessöffnungen wurden durchgeführt, um die Druckverteilung entlang der Zylinderoberfläche zu finden. Der Luftwiderstandskoeffizient wurde berechnet und stimmt gut mit anderen Quellen überein. Die Manipulation des Flusses, um einen turbulenten Grenzfluss bei relativ niedriger Reynoldszahl auszulösen, wurde ebenfalls demonstriert.
Referenzen
- d'Alembert, Jean le Rond (1752), Essai d'une nouvelle théorie de la résistance des fluides
- John D. Anderson (2017), Fundamentals of Aerodynamics, 6th Edition, ISBN: 978-1-259-12991-9, McGraw-Hill
- Prandtl, Ludwig (1904), Motion of fluids with very little viscosity, 452, NACA Technical Memorandum
pringen zu...
Videos aus dieser Sammlung:

Now Playing
Querzylindrische Strömung: Messung der Druckverteilung und Einschätzung des Strömungswiderstandskoeffizient
Aeronautical Engineering
16.1K Ansichten

Aerodynamisches Verhalten eines Modellflugzeugs: Die DC-6B
Aeronautical Engineering
8.3K Ansichten

Charakterisierung von Propellern: Variationen von Pitch, Durchmesser und Blattzahl, und deren Einfluss auf die Leistung
Aeronautical Engineering
26.2K Ansichten

Verhalten der Tragflächen: Druckverteilung über einem Clark Y-14-Flügel
Aeronautical Engineering
21.0K Ansichten

Clark Y-14 Tragflächenleistung: Einsatz von Hochauftriebsvorrichtungen (Klappen und Vorflügel)
Aeronautical Engineering
13.3K Ansichten

Turbulence Sphere-Methode: Bewertung der Strömungsqualität im Windkanal
Aeronautical Engineering
8.7K Ansichten

Analyse einer Düse: Variationen in Machzahl und Druck entlang einer konvergierenden und einer konvergierend-divergierenden Düse
Aeronautical Engineering
37.9K Ansichten

Schlieren-Imaging: Eine Technik zur Visualisierung der Eigenschaften von Überschallströmungen
Aeronautical Engineering
11.4K Ansichten

Strömungsvisualisierung in einem Wassertunnel: Beobachtung des Vorderkantenwirbels über einem Deltaflügel
Aeronautical Engineering
8.0K Ansichten

Surface Dye Flow Visualisierung: Eine qualitative Methode zur Beobachtung von Stromlinien in Überschallströmungen
Aeronautical Engineering
4.9K Ansichten

Pitotrohr: Ein Gerät zur Messung der Luftströmungsgeschwindigkeit
Aeronautical Engineering
48.7K Ansichten

Konstant-Temperatur-Anemometrie: Ein Werkzeug zur Untersuchung der turbulenten Grenzschichtströmung
Aeronautical Engineering
7.2K Ansichten

Druckwandler: Kalibrierung mit einem Pitotrohr
Aeronautical Engineering
8.5K Ansichten

Echtzeit-Flugsteuerung: Eingebettete Sensorkalibrierung und Datenerfassung
Aeronautical Engineering
10.2K Ansichten

Multicopter-Aerodynamik: Charakterisierung der Schubkraft bei einem Hexacopter
Aeronautical Engineering
9.1K Ansichten
Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten