Fluxo Cilíndrico Cruzado: Medição da Distribuição de Pressão e Estimando os Coeficientes de Arrasto
Visão Geral
Fonte: David Guo, College of Engineering, Technology, and Aeronautics (CETA), Southern New Hampshire University (SNHU), Manchester, New Hampshire
As distribuições de pressão e estimativas de arrasto para o fluxo cilíndrico cruzado têm sido investigadas há séculos. Pela teoria ideal do fluxo potencial inviscid, a distribuição de pressão em torno de um cilindro é verticalmente simétrica. A distribuição de pressão rio acima e rio abaixo do cilindro também é simétrica, o que resulta em uma força de arrasto de rede zero. No entanto, os resultados experimentais produzem padrões de fluxo muito diferentes, distribuições de pressão e coeficientes de arrasto. Isso ocorre porque a teoria potencial inviscida ideal assume o fluxo irrotacional, o que significa que a viscosidade não é considerada ou levada em conta ao determinar o padrão de fluxo. Isso difere significativamente da realidade.
Nesta demonstração, um túnel de vento é utilizado para gerar uma velocidade de ar especificada, e um cilindro com 24 portas de pressão é usado para coletar dados de distribuição de pressão. Esta demonstração ilustra como a pressão de um fluido real fluindo em torno de um cilindro circular difere dos resultados previstos com base no fluxo potencial de um fluido idealizado. O coeficiente de arrasto também será estimado e comparado com o valor previsto.
Princípios
O coeficiente de pressão não dimensional, Cp, para uma posição arbitrária na teoria ideal do fluxo potencial em qualquer posição angular, φ, na superfície de um cilindro circular é dado pela seguinte equação:

O coeficientede pressão C p é definido como:
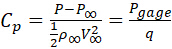
onde P é a pressão absoluta, P∞ é a pressão de fluxo livre não perturbada, Pgage = P − P∞ é a pressão de gárage, e  é a pressão dinâmica, que é baseada na densidade de fluxo livre, ρ∞, e airspeed, V∞.
é a pressão dinâmica, que é baseada na densidade de fluxo livre, ρ∞, e airspeed, V∞.
O padrão de fluxo previsto pela teoria ideal do fluxo potencial é mostrado na Figura 1. O fluxo é simétrico e, portanto, não há força de arrasto líquido zero. Isso se chama Paradoxo de D'Alembert [1].
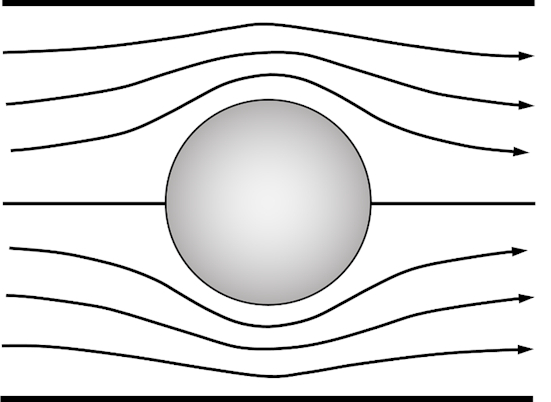
Figura 1. Padrão de fluxo de um fluxo transversal ideal em um túnel de vento.
No entanto, uma força de arrasto zero líquida não é esperada em condições reais de fluxo. A força de arrasto de um cilindro, FD,por comprimento unitário do cilindro devido a diferenças de pressão é dada por:

A integração é tomada ao longo do perímetro do cilindro.
Neste experimento, as medidas de pressão de gagem são coletadas de 24 portas de pressão ao longo do cilindro. Em seguida, a equação acima pode ser avaliada numericamente usando a pressão de gárage medida da seguinte forma:

onde Pgagei é a pressão de gárage na localização de φi, φi é a posição angular, r é o raio do cilindro, e 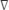 φ é a distância angular entre as portas adjacentes, que é de 15°. A pressão de gálagem é determinada usando um painel de manômetro com 24 colunas independentes, a pressão de gagem é determinada usando a seguinte equação:
φ é a distância angular entre as portas adjacentes, que é de 15°. A pressão de gálagem é determinada usando um painel de manômetro com 24 colunas independentes, a pressão de gagem é determinada usando a seguinte equação:

onde Δh é a diferença de altura do manômetro em referência à pressão de fluxo livre, ρL é a densidade do líquido no manômetro, e g é a aceleração devido à gravidade. Uma vez obtida a força de arrasto, o coeficiente de arrasto não-dimensional CD pode ser determinado através de:

onde d = 2r é o diâmetro do cilindro.
Lembrando o Paradoxo de D'Alembert, a força drag é devido aos efeitos negligenciados da viscosidade. Primeiro, uma camada de fronteira se desenvolve ao longo do cilindro como resultado de forças viscosas. Essas forças viscosas causam o arrasto de atrito na pele. Em segundo lugar, o cilindro é um objeto blefe (não simplificado). Isso cria a separação do fluxo e uma vigília de baixa pressão atrás dele e causa uma força de arrasto maior devido ao diferencial de pressão. A Figura 2 exibe vários padrões típicos de fluxo que são observados experimentalmente. Padrões de fluxo reais dependem do número de Reynolds, Re, que é definido como:
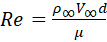
onde o parâmetro μ é a viscosidade dinâmica do fluido.

Figura 2. Vários tipos de padrões de fluxo sobre um cilindro.
Procedimento
1. Medir a distribuição de pressão em torno de um cilindro
- Remova a tampa superior da seção de teste de um túnel de vento e monte um cilindro de alumínio limpo (d = 4 in) com 24 portas embutidas em um toca-discos(Figura 3). Instale o cilindro para que a porta zero esteja voltada para cima(Figura 4a).
- Substitua a tampa superior e conecte os 24 tubos de pressão rotulados de 0 a 23 às portas correspondentes no painel do manômetro. O painel do manômetro deve ser preenchido com óleo colorido, mas marcado em água em.
- Ligue o túnel de vento e corra a 100 km/h. Registo todas as 24 medidas de pressão lendo o manômetro. Nesta velocidade, o número de Reynolds é 1,78 x 105. O padrão de fluxo esperado é mostrado na Figura 2d.
- Uma vez que todas as medidas tenham sido gravadas, desligue o túnel de vento e tape duas cordas (d = 1 mm) verticalmente no cilindro para criar o cilindro perturbado. Fita uma corda entre as portas 3 e 4 (φ = 52,5°) e a outra entre as portas 20 e 21 (φ = 307,5°). Certifique-se de que as portas próximas não estão bloqueadas pela fita, como mostrado na Figura 4b.
- Ligue o túnel de vento e repita o passo 3. Registo todas as medidas de pressão.

Figura 3. Layout de medição de pressão gárica do fluxo cilíndrico cruzado.

Figura 4. Instalação do cilindro no túnel de vento (as portas de pressão estão no meio do cilindro).

Figura 5. Painel de manômetro.
Resultados
Os resultados experimentais para o cilindro limpo e perturbado são mostrados nas Tabelas 1 e 2, respectivamente. Os dados podem ser plotados em um gráfico do coeficiente de pressão, Cp, versus posição angular, φ, para fluxo ideal e real, como mostrado na Figura 6.
| Porta de pressão # | Ângulo de posição q (°) | Pgage de leituras de manômetro (em. água) | Coeficiente de pressão calculado Cp |
| 0 | 0 | 1.7 | 1.00 |
| 1 | 15 | 1.4 | 0.83 |
| 2 | 30 | 0.0 | 0.01 |
| 3 | 45 | -1.7 | -0.98 |
| 4 | 60 | -2.7 | -1.57 |
| 5 | 75 | -3.7 | -2.15 |
| 6 | 90 | -3.3 | -1.92 |
| 7 | 105 | -3.0 | -1.74 |
| 8 | 120 | -3.2 | -1.86 |
| 9 | 135 | -3.2 | -1.86 |
| 10 | 150 | -3.3 | -1.92 |
| 11 | 165 | -3.5 | -2.03 |
| 12 | 180 | -3.4 | -1.97 |
Mesa 1. Resultados experimentais para o cilindro limpo. Devido à simetria, apenas dados para portas número 0-12 são mostrados.
| Porta de pressão # | Ângulo de posição q (°) | Pgage de leituras de manômetro (em. água) | Coeficiente de pressão calculado Cp |
| 0 | 0 | 1.8 | 1.05 |
| 1 | 15 | 1.6 | 0.93 |
| 2 | 30 | 0.6 | 0.35 |
| 3 | 45 | -1.3 | -0.73 |
| 4 | 60 | -2.9 | -1.69 |
| 5 | 75 | -4.0 | -2.31 |
| 6 | 90 | -4.0 | -2.33 |
| 7 | 105 | -1.7 | -0.99 |
| 8 | 120 | -1.5 | -0.89 |
| 9 | 135 | -1.4 | -0.84 |
| 10 | 150 | -1.4 | -0.84 |
| 11 | 165 | -1.5 | -0.87 |
| 12 | 180 | -1.4 | -0.84 |
Mesa 2. Resultados experimentais para o cilindro perturbado. Devido à simetria, apenas dados para portas número 0-12 são mostrados.

Figura 6. Distribuição do coeficiente de pressão, Cp, vs posição angular, φ, entre fluxo ideal e real.
No ponto de estagnação, φ = 0°, Cp atinge seu valor máximo de Cp = 1. Para φ < 60°, a distribuição do coeficiente de pressão é semelhante para as três curvas. É aqui que o fluxo da camada de limite laminar é anexado à superfície do cilindro. Para φ > 60°, os dois padrões experimentais de fluxo se desviam do fluxo ideal; eles formam uma região de baixa pressão na parte de trás do cilindro, que é preenchido com vórtices turbulentos e redemoinhos. Esta é a chamada região de vigília. É a diferença de pressão entre a frente e a parte de trás do cilindro que causa o grande arrasto que é observado no fluxo cilíndrico cruzado.
Apesar da semelhança nos padrões de fluxo entre o cilindro limpo e o cilindro perturbado, também há diferenças. O fluxo perturbado tende a envolver o cilindro mais antes da separação do fluxo, e também tem uma pressão mais alta nas costas. Isso causa menos arrasto, o que é verificado pelos cálculos de arrasto. Isso ocorre porque o fluxo laminar na frente do cilindro tem uma tendência a fluir em linha reta e é difícil para o fluxo envolver em torno do cilindro. Para o cilindro perturbado, o fluxo imediatamente transita para um fluxo turbulento e, assim, pode envolver o cilindro mais do que o cilindro limpo.
| Configurações de fluxo | Coeficiente de arrasto, CD |
| 1. Cilindro limpo | 1.68 |
| 2. Cilindro perturbado | 0.78 |
Mesa 4. Coeficiente de arrasto, CD (reynolds número Re = 1,78 x 105).
O coeficiente de arrasto CD para cilindro limpo a velocidade de ar de 60 mph ou Re = 178.000 foi avaliado experimentalmente e é aproximadamente 1,5 [2], o que é próximo do valor de 1,68 que foi obtido neste experimento para um cilindro limpo.
Dos resultados experimentais anteriores [2], o coeficiente de arrasto CD cai em Re = 3 x 105. Isso ocorre porque a transição do fluxo laminar para o fluxo turbulento ocorre naturalmente mesmo com um cilindro liso. No experimento, a transição de fluxo turbulenta é observada simplesmente gravando uma corda de 1 mm de diâmetro na superfície do cilindro. Assim, um coeficiente de arrasto menor CD de apenas 0,78 é obtido para o cilindro perturbado.
Aplicação e Resumo
O fluxo cilíndrico cruzado tem sido investigado teoricamente e experimentalmente desde o século XVIII. Encontrar as discrepâncias entre os dois nos permite expandir nossa compreensão da dinâmica dos fluidos e explorar novas metodologias. A teoria do fluxo de camadas de fronteira foi desenvolvida por Prandtl [3] no início do século XX, e é um bom exemplo da extensão do fluxo inviscid para a teoria do fluxo viscid na resolução do Paradoxo de D'Alembert.
Neste experimento, o fluxo cilíndrico cruzado foi investigado em um túnel de vento e as 24 portas de medição de pressão foram feitas para encontrar a distribuição de pressão ao longo da superfície do cilindro. O coeficiente de arrasto foi calculado e concorda bem com outras fontes. A manipulação do fluxo para desencadear o fluxo de fronteira turbulento no número relativo baixo de Reynolds também foi demonstrada.
Referências
- d'Alembert, Jean le Rond (1752), Essai d'une nouvelle théorie de la résistance des fluides
- John D. Anderson (2017), Fundamentals of Aerodynamics, 6th Edition, ISBN: 978-1-259-12991-9, McGraw-Hill
- Prandtl, Ludwig (1904), Motion of fluids with very little viscosity, 452, NACA Technical Memorandum
Pular para...
Vídeos desta coleção:

Now Playing
Fluxo Cilíndrico Cruzado: Medição da Distribuição de Pressão e Estimando os Coeficientes de Arrasto
Aeronautical Engineering
16.1K Visualizações

Desempenho Aerodinâmico de um Aeromodelo: O DC-6B
Aeronautical Engineering
8.3K Visualizações

Caracterização da hélice: variações no passo, diâmetro e número de pás no desempenho
Aeronautical Engineering
26.2K Visualizações

Comportamento do aerofólio: Distribuição de pressão sobre uma asa Clark Y-14
Aeronautical Engineering
21.0K Visualizações

Desempenho da asa Clark Y-14: Implantação de dispositivos de alta sustentação (Flaps e Slats)
Aeronautical Engineering
13.3K Visualizações

Método da esfera de turbulência: avaliando a qualidade do fluxo do túnel de vento
Aeronautical Engineering
8.7K Visualizações

Análise de bocais: variações no número de Mach e na pressão ao longo de um bocal convergente e convergente-divergente
Aeronautical Engineering
37.9K Visualizações

Imageamento de Schlieren: uma técnica para visualizar recursos de fluxo supersônico
Aeronautical Engineering
11.4K Visualizações

Visualização de fluxo em um túnel de água: observando o vórtice de ponta sobre uma asa delta
Aeronautical Engineering
8.0K Visualizações

Visualização de fluxo com corante de superfície: um método qualitativo para observar padrões de estrias em fluxo supersônico
Aeronautical Engineering
4.9K Visualizações

Tubo Pitot-estático: um dispositivo para medir a velocidade do fluxo de ar
Aeronautical Engineering
48.7K Visualizações

Anemometria de temperatura constante: uma ferramenta para estudar o fluxo em camada limite turbulenta
Aeronautical Engineering
7.2K Visualizações

Transdutor de Pressão: Calibração Usando um Tubo Pitot-estático
Aeronautical Engineering
8.5K Visualizações

Controle de Voo em Tempo Real: Calibração de Sensor Incorporado e Aquisição de Dados
Aeronautical Engineering
10.2K Visualizações

Aerodinâmica de Multicópteros: Caracterizando o Empuxo em um Hexacóptero
Aeronautical Engineering
9.1K Visualizações
Copyright © 2025 MyJoVE Corporation. Todos os direitos reservados