Flusso cilindrico incrociato: misurazione della distribuzione della pressione e stima dei coefficienti di resistenza
Panoramica
Fonte: David Guo, College of Engineering, Technology, and Aeronautics (CETA), Southern New Hampshire University (SNHU), Manchester, New Hampshire
Le distribuzioni di pressione e le stime di resistenza per il flusso cilindrico incrociato sono state studiate per secoli. Secondo la teoria del flusso potenziale inviscido ideale, la distribuzione della pressione attorno a un cilindro è verticalmente simmetrica. Anche la distribuzione della pressione a monte e a valle del cilindro è simmetrica, il che si traduce in una forza di resistenza netta zero. Tuttavia, i risultati sperimentali producono modelli di flusso, distribuzioni di pressione e coefficienti di resistenza molto diversi. Questo perché la teoria del potenziale inviscido ideale presuppone un flusso irrotazionale, il che significa che la viscosità non viene considerata o presa in considerazione quando si determina il modello di flusso. Questo differisce significativamente dalla realtà.
In questa dimostrazione, una galleria del vento viene utilizzata per generare una velocità dell'aria specificata e un cilindro con 24 porte di pressione viene utilizzato per raccogliere i dati di distribuzione della pressione. Questa dimostrazione illustra come la pressione di un fluido reale che scorre attorno a un cilindro circolare differisca dai risultati previsti in base al flusso potenziale di un fluido idealizzato. Anche il coefficiente di resistenza aerodinamica sarà stimato e confrontato con il valore previsto.
Principi
Il coefficiente di pressione non dimensionale, Cp, per una posizione arbitraria nella teoria del flusso potenziale ideale in qualsiasi posizione angolare, θ, sulla superficie di un cilindro circolare è dato dalla seguente equazione:

Il coefficiente di pressione Cp è definito come:
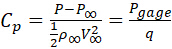
dove P è la pressione assoluta, P∞ è la pressione a flusso libero indisturbata, Pgage = P − P∞ è la pressione del misuratore, ed  è la pressione dinamica, che si basa sulla densità del flusso libero, ρ∞, e velocità dell'aria, V∞.
è la pressione dinamica, che si basa sulla densità del flusso libero, ρ∞, e velocità dell'aria, V∞.
Il modello di flusso previsto dalla teoria del flusso potenziale ideale è mostrato nella Figura 1. Il flusso è simmetrico e quindi non vi è alcuna forza di resistenza netta. Questo è chiamato Paradosso di D'Alembert [1].
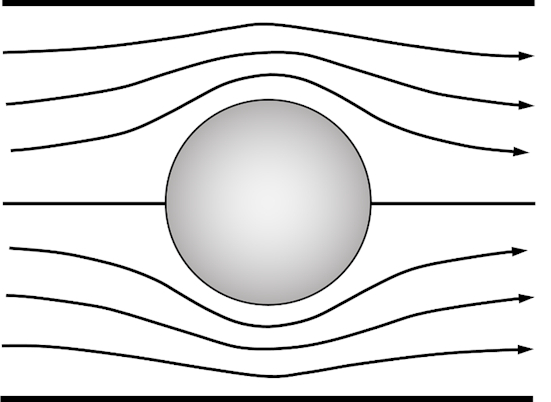
Figura 1. Modello di flusso di un flusso cilindrico incrociato ideale in una galleria del vento.
Tuttavia, non è prevista una forza di resistenza netta zero in condizioni di flusso reali. La forza di trascinamento di un cilindro, FD,per unità di lunghezza del cilindro dovuta alle differenze di pressione è data da:

L'integrazione viene presa lungo il perimetro del cilindro.
In questo esperimento, le misurazioni della pressione del misuratore vengono raccolte da 24 porte di pressione lungo il cilindro. Quindi, l'equazione di cui sopra può essere valutata numericamente utilizzando la pressione misurata come segue:

dove P gage i è la pressione del misuratore nella posizione di θi, θi è la posizione angolare, r è il raggio del cilindro e  θ è la distanza angolare tra le porte adiacenti, che è 15°. La pressione del misuratore viene determinata utilizzando un pannello manometro con 24 colonne indipendenti, la pressione del misuratore viene determinata utilizzando la seguente equazione:
θ è la distanza angolare tra le porte adiacenti, che è 15°. La pressione del misuratore viene determinata utilizzando un pannello manometro con 24 colonne indipendenti, la pressione del misuratore viene determinata utilizzando la seguente equazione:

dove Δh è la differenza di altezza del manometro in riferimento alla pressione del flusso libero, ρL è la densità del liquido nel manometro e g è l'accelerazione dovuta alla gravità. Una volta ottenuta la forza di trascinamento, il coefficiente di resistenza non dimensionale CD può essere determinato attraverso:

dove d = 2r è il diametro del cilindro.
Ricordando il Paradosso di D'Alembert, la forza di trascinamento è dovuta agli effetti trascurati della viscosità. In primo luogo, uno strato limite si sviluppa lungo il cilindro a causa di forze viscose. Queste forze viscose causano la resistenza all'attrito della pelle. In secondo luogo, il cilindro è un oggetto bluff (non aerodinamico). Ciò crea una separazione del flusso e una scia a bassa pressione dietro di esso e provoca una forza di resistenza maggiore a causa del differenziale di pressione. Nella Figura 2 vengono visualizzati diversi modelli di flusso tipici osservati sperimentalmente. I modelli di flusso reali si basano sul numero di Reynolds, Re, che è definito come:
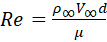
dove il parametro μ è la viscosità dinamica del fluido.

Figura 2. Vari tipi di modelli di flusso su un cilindro.
Procedura
1. Misurare la distribuzione della pressione attorno a un cilindro
- Rimuovere il coperchio superiore della sezione di prova di una galleria del vento e montare un cilindro di alluminio pulito (d = 4 pollici) con 24 porte integrate su un giradischi (Figura 3). Installare il cilindro in modo che la porta zero sia rivolta a monte (Figura 4a).
- Sostituire il coperchio superiore e collegare i 24 tubi di pressione etichettati 0 - 23 alle porte corrispondenti sul pannello del manometro. Il pannello manometro deve essere riempito con olio colorato ma contrassegnato in acqua in. graduazioni (Figura 5).
- Accendi la galleria del vento e corri a 60 mph. Registra tutte le 24 misurazioni della pressione leggendo il manometro. A questa velocità dell'aria, il numero di Reynolds è 1,78 x 105. Il modello di flusso previsto è illustrato nella Figura 2d.
- Una volta registrate tutte le misurazioni, spegnere la galleria del vento e incollare due stringhe (d = 1 mm) verticalmente sul cilindro per creare il cilindro disturbato. Nastro una stringa tra le porte 3 e 4 (θ = 52,5°) e l'altra tra le porte 20 e 21 (θ = 307,5°). Assicurarsi che le porte vicine non siano bloccate dal nastro, come illustrato nella Figura 4b.
- Accendere la galleria del vento e ripetere il passaggio 3. Registrare tutte le misurazioni della pressione.

Figura 3. Layout di misurazione della pressione del misuratore di flusso cilindrico incrociato.

Figura 4. Configurazione del cilindro nella galleria del vento (le porte di pressione sono al centro del cilindro).

Figura 5. Pannello manometro.
Risultati
I risultati sperimentali per il cilindro pulito e disturbato sono mostrati rispettivamente nelle tabelle 1 e 2. I dati possono essere tracciati in un grafico del coefficiente di pressione, Cp, contro posizione angolare, θ, per il flusso ideale e reale come mostrato in Figura 6.
| Porta di pressione # | Angolo di posizione q (°) | Misuratore P dalleletture del manometro (in. acqua) | Coefficiente di pressione calcolato Cp |
| 0 | 0 | 1.7 | 1.00 |
| 1 | 15 | 1.4 | 0.83 |
| 2 | 30 | 0.0 | 0.01 |
| 3 | 45 | -1.7 | -0.98 |
| 4 | 60 | -2.7 | -1.57 |
| 5 | 75 | -3.7 | -2.15 |
| 6 | 90 | -3.3 | -1.92 |
| 7 | 105 | -3.0 | -1.74 |
| 8 | 120 | -3.2 | -1.86 |
| 9 | 135 | -3.2 | -1.86 |
| 10 | 150 | -3.3 | -1.92 |
| 11 | 165 | -3.5 | -2.03 |
| 12 | 180 | -3.4 | -1.97 |
Tabella 1. Risultati sperimentali per il cilindro pulito. A causa della simmetria, vengono visualizzati solo i dati per le porte numero 0-12.
| Porta di pressione # | Angolo di posizione q (°) | Misuratore P dalleletture del manometro (in. acqua) | Coefficiente di pressione calcolato Cp |
| 0 | 0 | 1.8 | 1.05 |
| 1 | 15 | 1.6 | 0.93 |
| 2 | 30 | 0.6 | 0.35 |
| 3 | 45 | -1.3 | -0.73 |
| 4 | 60 | -2.9 | -1.69 |
| 5 | 75 | -4.0 | -2.31 |
| 6 | 90 | -4.0 | -2.33 |
| 7 | 105 | -1.7 | -0.99 |
| 8 | 120 | -1.5 | -0.89 |
| 9 | 135 | -1.4 | -0.84 |
| 10 | 150 | -1.4 | -0.84 |
| 11 | 165 | -1.5 | -0.87 |
| 12 | 180 | -1.4 | -0.84 |
Tabella 2. Risultati sperimentali per il cilindro disturbato. A causa della simmetria, vengono visualizzati solo i dati per le porte numero 0-12.

Figura 6. Distribuzione del coefficiente di pressione, Cp, vs posizione angolare, θ, tra flusso ideale e reale.
Nel punto di ristagno, θ = 0°, Cp raggiunge il suo valore massimo di Cp = 1. Per θ < 60°, la distribuzione del coefficiente di pressione è simile per tutte e tre le curve. È qui che il flusso dello strato limite laminare è attaccato alla superficie del cilindro. Per θ > 60°, i due modelli di flusso sperimentali si discostano dal flusso ideale; formano una regione di bassa pressione nella parte posteriore del cilindro, che è piena di vortici e vortici turbolenti. Questa è la cosiddetta regione della scia. È la differenza di pressione tra la parte anteriore e posteriore del cilindro che causa la grande resistenza che si osserva nel flusso cilindrico incrociato.
Nonostante la somiglianza nei modelli di flusso tra il cilindro pulito e il cilindro disturbato, ci sono anche differenze. Il flusso disturbato tende ad avvolgere il cilindro più prima della separazione del flusso e ha anche una ripressione più elevata. Ciò causa meno trascinamento, che viene verificato dai calcoli di trascinamento. Ciò si verifica perché il flusso laminare nella parte anteriore del cilindro ha la tendenza a fluire dritto ed è difficile per il flusso avvolgere il cilindro. Per il cilindro disturbato, il flusso passa immediatamente in un flusso turbolento e quindi può avvolgere il cilindro più del cilindro pulito.
| Configurazioni di flusso | Coefficiente di resistenza, CD |
| 1. Cilindro pulito | 1.68 |
| 2. Cilindro disturbato | 0.78 |
Tabella 4. Coefficiente di resistenza, CD (numero di Reynolds Re = 1,78 x 105).
Il coefficiente di resistenza CD per cilindro pulito a 60 mph di velocità dell'aria o Re = 178.000 è stato valutato sperimentalmente ed è di circa 1,5 [2], che è vicino al valore di 1,68 che è stato ottenuto in questo esperimento per un cilindro pulito.
Dai precedenti risultati sperimentali [2], il coefficiente di resistenza CD scende a Re = 3 x 105. Questo perché il passaggio dal flusso laminare al flusso turbolento avviene naturalmente anche con un cilindro liscio. Nell'esperimento, la transizione del flusso turbolento viene osservata semplicemente nastrando una corda di 1 mm di diametro alla superficie del cilindro. Pertanto, si ottiene un coefficiente di resistenza inferiore CD di solo 0,78 per il cilindro disturbato.
Applicazione e Riepilogo
Il flusso cilindrico incrociato è stato studiato teoricamente e sperimentalmente dal 18 ° secolo. Trovare le discrepanze tra i due ci consente di espandere la nostra comprensione della fluidodinamica ed esplorare nuove metodologie. La teoria del flusso dello strato limite è stata sviluppata da Prandtl [3] all'inizio del 20 ° secolo, ed è un buon esempio dell'estensione del flusso inviscido alla teoria del flusso viscido nella risoluzione del paradosso di D'Alembert.
In questo esperimento, il flusso cilindrico incrociato è stato studiato in una galleria del vento e sono state effettuate le 24 porte di misurazione della pressione per trovare la distribuzione della pressione lungo la superficie del cilindro. Il coefficiente di resistenza aerodinamica è stato calcolato e concorda bene con altre fonti. È stata anche dimostrata la manipolazione del flusso per innescare un flusso limite turbolento a un numero di Reynolds relativamente basso.
Riferimenti
- d'Alembert, Jean le Rond (1752), Essai d'une nouvelle théorie de la résistance des fluides
- John D. Anderson (2017), Fundamentals of Aerodynamics, 6th Edition, ISBN: 978-1-259-12991-9, McGraw-Hill
- Prandtl, Ludwig (1904), Motion of fluids with very little viscosity, 452, NACA Technical Memorandum
Vai a...
Video da questa raccolta:

Now Playing
Flusso cilindrico incrociato: misurazione della distribuzione della pressione e stima dei coefficienti di resistenza
Aeronautical Engineering
16.1K Visualizzazioni

Prestazioni aerodinamiche di un aeromodello: il DC-6B
Aeronautical Engineering
8.3K Visualizzazioni

Caratterizzazione dell'elica: variazioni di passo, diametro e numero di pale sulle prestazioni
Aeronautical Engineering
26.1K Visualizzazioni

Comportamento del profilo alare: distribuzione della pressione su un'ala Clark Y-14
Aeronautical Engineering
21.0K Visualizzazioni

Clark Y-14 Wing Performance: implementazione di dispositivi ad alto sollevamento (flap e lamelle)
Aeronautical Engineering
13.3K Visualizzazioni

Metodo della sfera di turbolenza: valutazione della qualità del flusso nella galleria del vento
Aeronautical Engineering
8.7K Visualizzazioni

Analisi degli ugelli: variazioni del numero di Mach e della pressione lungo un ugello convergente e un ugello convergente-divergente
Aeronautical Engineering
37.8K Visualizzazioni

Schlieren Imaging: una tecnica per visualizzare le caratteristiche del flusso supersonico
Aeronautical Engineering
11.4K Visualizzazioni

Visualizzazione del flusso in un tunnel d'acqua: osservazione del vortice di estremità su un'ala delta
Aeronautical Engineering
8.0K Visualizzazioni

Visualizzazione del flusso di colorante superficiale: un metodo qualitativo per osservare le linee di flusso nel flusso supersonico
Aeronautical Engineering
4.9K Visualizzazioni

Tubo Pitot-statico: un dispositivo per misurare la velocità del flusso d'aria
Aeronautical Engineering
48.7K Visualizzazioni

Anemometria a temperatura costante: uno strumento per studiare il flusso turbolento dello strato limite
Aeronautical Engineering
7.2K Visualizzazioni

Trasduttore di pressione: calibrazione mediante tubo statico Pitot
Aeronautical Engineering
8.5K Visualizzazioni

Controllo di volo in tempo reale: calibrazione del sensore incorporato e acquisizione dati
Aeronautical Engineering
10.1K Visualizzazioni

Aerodinamica multirotore: caratterizzazione della spinta su un esacottero
Aeronautical Engineering
9.1K Visualizzazioni