דינמיקה של מבנים

יש הבדל מהותי בין עומסי הכבידה הרגילים (משקל עצמי) הפועלים על מבנה, שהם מעין-סטטיים (כלומר, הם משתנים לאט מאוד, או בכלל לא עם הזמן), לבין אלה המיוצרים על ידי הוריקנים, פיצוצים ורעידות אדמה, שהם דינמיים מאוד בטבע. במקרה של הוריקנים ועומסי רוח אחרים, ניתן לדגמן את השפעותיהם כלחץ סטטי שווה ערך במעבדה שכן תדירות הרוחות ארוכה מאוד בהשוואה לתדירות הטבעית הבסיסית של המבנה הטיפוסי. חריגים חשובים לכך כוללים מבנים גמישים, כגון גשרים ארוכי טווח שהותו בכבלים ומתלים, תרנים גבוהים ומבני טורבינות רוח, שבהם התדירות הטבעית של המבנה יכולה להתאים לזה של משבי הרוח או הרוחות הישרות. במקרה של רעידות אדמה, העומסים הם בעיקר אינרציאליים כמו הקרקע נעה, והמבנה נוטה להישאר עדיין. במקרה זה, הטעינה תלויה במסה בפועל, נוקשות ושיכוך המבנה, וכמויות העניין הן התאוצות, המהירויות והתזוזות סביב המבנה. קבוצה שנייה זו של כמויות קשה מאוד לשחזר במדויק במעבדה אם שולחנות לנער אינם זמינים.

באמצעות פיזיקה בסיסית, כמו החוק השני של ניוטון, ניתן לפשט את בעיית שיווי המשקל של מבנה (כגון גשר או מסגרת עם קרן נוקשה), הכפופה לתנועות קרקעיות (u_g), לזו של מסה אחת של דרגת חופש (מ ')עם נוקשות (k) ומאפייני שיכוך (c). שני האחרונים יכולים להיות מיוצגים על ידי קפיץ שבו הכוח פרופורציונלי לעקירה (u) וכן נקודה שבה הכוחות פרופורציונליים למהירות (v) (איור 1). ניתן לשלב רכיבים אלה במקביל ו/או סדרה כדי לדגמן תצורות מבניות שונות.

נוקשות מוגדרת ככוח הנדרש כדי לעוות את המבנה על ידי כמות יחידה. נניח שאדם טוען קרן cantilever עם כוח ידוע (P) ומודד את העיוות האלסטי שלה בקצה ( 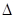). הנוקשות מוגדרת כ- k = P / 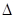. עבור מערכת הקנטילוור האלסטית הפשוטה המוצגת, k = L³/3EI, כאשר L הוא אורך הקנטילוור, אני רגע האינרציה שלו, ו- E הוא מודולוס של יאנג לחומר המשמש. לאחר מכן, תארו לעצמכם מה קורה אם אחד מסיר את הכוח פתאום, ובכך מאפשר הקנטילוור לרטוט. אחד באופן אינטואיטיבי יצפה משרעת של תנודות להתחיל לרדת עם כל מחזור. תופעה זו נקראת שיכוך ומתייחסת לסדרה של מנגנונים פנימיים מורכבים, כגון חיכוך, הנוטים להפחית את התנודות. הכימות של שיכוך מתואר מאוחר יותר במעבדה זו, אבל חשוב לציין כי בשלב זה, לא הרבה ידוע על מנגנונים אלה מנקודת מבט תיאורטית או מעשית. מושג שימושי הוא לדמיין את מקדם שיכוך קריטי (c_cr), אשר מתאים למקרה שבו cantilever יבוא לנוח לאחר תנודה מלאה אחת בלבד.

איור 1: מודל מערכת חופש מדרגה אחת.

כתיבת משוואה של שיווי משקל אופקי של כוחות למערכת המוצגת באיור 1 מובילה ל:

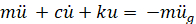(א"ק 1)

אם נסתכל לרגע על מקרה פשוט יותר, שבו נוכל להתעלם מההשפעות שלו זניחות, ואין פונקציית כפייה חיצונית, משוואה 1 הופכת למשוואה הדיפרנציאלית ההומוגנית הליניארית מסדר שני:

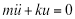(א"ק 2)

שהפתרון שלו הוא של הטופס:

(א"ק 3)

הבחנה פעמיים תיתן לנו:

(א"ק 4)

החלפת משוואה 4 במשוואה 2, תשואות:

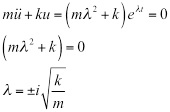(א"ק 5)

הפתרון הכללי הוא:

(א"ק 6)

איפה התדר הטבעי הלא מפות של המערכת.

אם מערכת זו מקבלת תזוזה ראשונית ( ) ו/או מהירות התחלתית ( 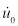), משוואה 6 הופכת:

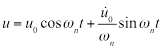(א"ק 7)

אם נוסיף את ההשפעה של שיכוך (c) ולהגדיר, התדירות הטבעית הפגומה של המערכת הופכת שווה ערך למשוואה 7 היא:

(א"ק 8)

במקרה של תזוזה ראשונית u₀, איור 2 מציג את אופן הפעולה עבור מספר ערכים של .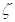

איור 2: השפעת שיכוך על תנודות חופשיות: הגדרת שיכוך קריטי (עליון); חישוב שיכוך מצו לוגריתמי (נמוך יותר).

אם באיור 2, אחד מגדיר , כאשר u_n ו- u_n+1 הם ההעתק במחזורים רצופים, אז:

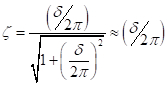(א"ק 9)

חוזר למשוואה 1, אם תנועת הקרקע נלקחת כפונקציה סינוסואידלית 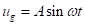, האנלוגי של משוואה 8 הוא:

(א"ק 10)

איפה הפיגור של הפאזה, ו-R_a הוא גורם התגובה להגברה, שהעלילות שלו מודגמות באיור 3. איור 3 מראה כי עבור ערכים נמוכים של שיכוך 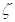(<0.2), כאשר תדירות פונקציית הכפייה מתקרבת לתדירות הטבעית של המערכת, תגובת המערכת הופכת לבלתי יציבה, תופעה המכונה בדרך כלל תהודה.

איור 3: תגובת תזוזה, מהירות ותאוצה.

במעבדה זו, נחקור באופן ניסיוני את המושגים והנגזרים שמאחורי משוואות 1-10 בהקשר של הדינמיקה של מבנים המשתמשים בטבלת ניעור.

ראשית, קבע את התדירות (ω) שבה אירעה ההעתקה המרבית עבור כל דגם. הנוסחה הפשוטה המקורית שנידונה לעיל, 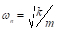צריכה להשתנות מכיוון שמסת הקרן עצמה (m_b = W_beam/g),המופצת על גובהה, אינה זניחה בהשוואה למסה בחלק העליון (m = W_block/g). המסה המקבילה למקרה של קרן cantilever היא (m +0.23m_b),כאשר m הוא המסה בחלק העליון ו m_b היא המסה המבוזרת של הקרן. הנוקשות k ניתנת על ידי ההדדיות של העיוות ( 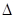) הנגרמת בחלק העליון של הקנטילוור על ידי כוח יחידה:

(א"ק 11)

כאשר L הוא אורך הקרן, E הוא מודולוס של גמישות, ואני הרגע של אינרציה. אני ניתן על ידי , שבו b הוא הרוחב ו h הוא עובי הקרן. לפיכך, התדירות המעגלית הטבעית של קרן cantilever, כולל המשקל העצמי שלה היא:

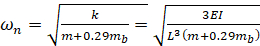(א"ק 12)

בהתבסס על משוואה זו, התדרים הטבעיים החזויים מחושבים בטבלה 1.

מספר קרן	אורך (ב)	רוחב (ב.)	עבה. (ב.)	אני (ב.4)	E (ksi)	משקל (ק"ג)	משקל קרן (ק"ג).	מסה יעילה (ליברות שניה.2/אינץ')	תדירות טבעית (מחזורים לשניה)
1	12.0	1.002	0.124	1.59E-04	10200	0.147	0.149	4.70E-04	2.45
2	16.0	1.003	0.124	1.59E-04	10200	0.146	0.199	4.97E-04	1.55
3	20.0	1.002	0.125	1.63E-04	10200	0.146	0.251	5.28E-04	1.09
4	24.0	1.003	0.125	1.63E-04	10200	0.148	0.301	5.63E-04	0.80
5	28.0	1.001	0.125	1.63E-04	10200	0.144	0.350	5.82E-04	0.62
6	32.0	1.000	0.124	1.59E-04	10200	0.146	0.397	6.15E-04	0.49
7	36.0	1.002	0.126	1.67E-04	10200	0.147	0.455	6.52E-04	0.41
8	40.00	1.000	0.125	1.63E-04	10200	0.148	0.500	6.81E-04	0.34

טבלה 1: תדרים טבעיים של קורות הקנטילוור שנבדקו.

הערכים הנמדדים והתיאורטיים של התדר הרגיל עבור מערכות המודל שלנו מועווים בטבלה 2. התדרים הטבעיים בפועל חושבו על ידי תזוזה זהירה של קרן הקנטילוור ב-1 אינץ' ואז התבוננות בתזוזה לעומת תגובת הזמן. ההשוואה שלהלן נעשית במונחים של תקופות (T_{d ,} ב sec.) כפי שנקבעו מ- T_d = u₀-u₁, כפי שמוצג באיור 2(ב). זה דורש טיפול וסבלנות כדי להשיג תוצאות אמינות. ההפגנות שהוצגו נועדו רק לתת המחשה כוללת להתנהגות המערכת.

מספר קרן	תדירות טבעית (מחזורים לשניה)	תקופה צפויה (שניה)	תקופה בפועל (שניה)	שגיאה (%)
1	2.45	2.56	2.65	-3.33%
2	1.55	4.06	4.23	-4.22%
3	1.09	5.78	6.79	-17.52%
4	0.80	7.84	8.04	-2.54%
5	0.62	10.06	10.63	-5.70%
6	0.49	12.79	13.04	-1.97%
7	0.41	15.32	16.78	-9.50%
8	0.34	18.59	20.56	-10.59%

טבלה 2. השוואת תוצאות.

ההבדלים נובעים בעיקר מהעובדה כי הקורות אינן מחוברות בקשיחות לבסיס העץ, והגמישות הנוספה בבסיס מגדילה את תקופת המבנה. מקור שגיאה נוסף הוא כי שיכוך לא היה בחשבון בחישובים, כי שיכוך קשה מאוד למדוד משרעת תלויה.

לאחר מכן, מכל אחת מההיסטוריה של ההעתקה לעומת היסטוריה של זמן, חלצו את הערך המרבי של כל תדר והתוו את גודל ההעתק לעומת תדר מנורמל כמו זה באיור 3. דוגמה לכך מוצגת באיור 4, שבו יש לנו תדר מנורמל לעומת התדר הטבעי הראשון (Beam Number 1) והתוותנו את ההעתקה המרבית של קרן זו כאשר שולחן השייק היה נתון לעיוות סינוסואידי משתנה עם משרעת של 1 ב.

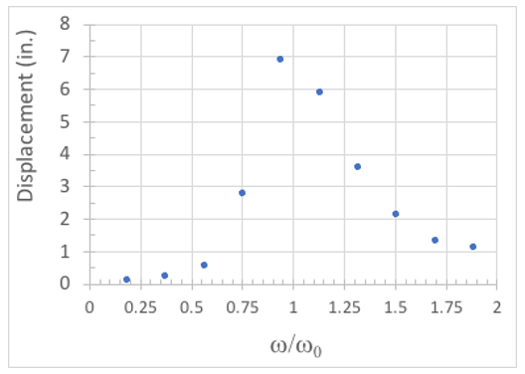
איור 4: עיוות של #1 קרן לעומת תדר טבלה מנורמל.

בתחילה, כאשר היחס של ω/ω_n קטן, אין הרבה תגובה כמו קלט האנרגיה מתנועת השולחן אינו מרגש את המודל. ככל ש- ω/ω_n מתקרב 1, יש עלייה משמעותית מאוד בתגובה, עם העיוותים הופכים גדולים למדי. התגובה המרבית מגיעה כאשר ω/ω_n קרוב מאוד ל- 1. ככל שהתדירות המנורמלת גדלה מעבר ל- ω/ω_n = 1, התגובה הדינמית מתחילה למות; כאשר ω/ω_n הופך להיות גדול אנחנו נמצאים במצב שבו העומס מוחל לאט מאוד ביחס לתדירות הטבעית של המבנה, ואת העיוות צריך להיות שווה לזה מעומס מיושם סטטית.

מטרת הניסויים הללו היא בעיקר להראות את השינויים בהתנהגות באופן איכותי, כפי שניתן לראות בהפגנות עבור שני מבני המסגרות. השגת תוצאות דומות לאלה באיורים 3 ו-4 דורשת טיפול וסבלנות רבה כמקורות חיכוך ודומה ישפיעו על כמות העיקולים ובכך יעבירו את העקומות בדומה לאלו באיור 3(ג) שמאלה או ימינה כתדירות הפגועה בפועל, 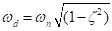משתנה.

בניסוי זה, התדירות הטבעית והשיכוך של מערכת cantilever פשוטה נמדדו באמצעות שולחנות לנער. למרות שתוכן התדירות של רעידת אדמה הוא אקראי ומכסה רוחב פס גדול של תדרים, ספקטרום תדרים יכול להתפתח על ידי תרגום היסטוריית זמן ההאצה לתחום התדרים באמצעות התמרת פורייה. אם התדרים השולטים של התנועה הקרקעית תואמים את זה של המבנה, סביר להניח כי המבנה יעבור עקירה גדולה וכתוצאה מכך ייחשף לנזק רב או אפילו לקריסתו. עיצוב סייסמי בוחן את רמות התאוצה הצפויות מרעידת אדמה במיקום נתון בהתבסס על תיעוד היסטורי, מרחק למקור רעידת האדמה, סוג וגודל מקור רעידת האדמה, וההאצה של גלי פני השטח והגוף כדי לקבוע רמה סבירה של תאוצה שתשמש לתכנון.

מה שהציבור הרחב לעתים קרובות לא מבין הוא שהוראות העיצוב הסיסמי הנוכחי נועדו רק למזער את ההסתברות לקריסה ואובדן חיים במקרה שרעידת אדמה אמינה מקסימלית מתרחשת לרמה מקובלת (בסביבות 5% עד 10% ברוב המקרים). בעוד שעיצובים מבניים כדי להשיג הסתברויות נמוכות יותר לכישלון אפשריים, הם מתחילים להיות לא-קומיים. צמצום הפסדים ושיפור החוסן לאחר אירוע כזה אינם נחשבים כיום במפורש, אם כי שיקולים כאלה הופכים נפוצים יותר, שכן פעמים רבות התוכן של בניין ופונקציונליותו עשויים להיות חשובים הרבה יותר מאשר הבטיחות שלו. קחו למשל את המקרה של תחנת כוח גרעינית (כמו פוקושימה ברעידת האדמה הגדולה של קאנטו ב-2011), בניין מגורים בן עשר קומות בלוס אנג'לס, או מתקן לייצור שבבי מחשב בעמק הסיליקון ואת חשיפתם ופגיעותם לאירועים סיסמיים.

במקרה של תחנת הכוח הגרעינית, רצוי לתכנן את המבנה כדי למזער כל נזק בהתחשב בכך שלתוצאה של אפילו כשל מינימלי יכולות להיות השלכות חמורות מאוד. במקרה זה, עלינו לנסות לאתר מתקן זה רחוק ככל האפשר ממקורות רעידת אדמה כדי למזער את החשיפה, כי מזעור הפגיעות לרמה הרצויה הוא קשה מאוד ויקר. המציאות היא שזה יקר מאוד לעשות את זה בהתחשב ברצון של הציבור להימנע לא רק תקרית מסוג פוקושימה, אלא גם אחד מוגבל יותר, כמו האסון הגרעיני על האי שלושה קילומטרים.

עבור הבניין הרב קומות בלוס אנג'לס, קשה יותר למזער את החשיפה מכיוון שרשת גדולה של תקלות סייסמיות עם תקופות החזרה לא ידועות במקצת נמצאת בקרבת מקום, כולל שבר סן אנדריאס. במקרה זה, הדגש צריך להיות על תכנון ופרטים חזקים כדי למזער את הפגיעות של המבנה; בעלי המגורים צריכים להיות מודעים לכך שהם לוקחים סיכון משמעותי אם מתרחשת רעידת אדמה. הם לא צריכים לצפות שהבניין יקרוס, אבל הבניין עשוי להיות אובדן מוחלט אם רעידת האדמה היא בסדר גודל מספיק גדול.

עבור מפעל שבב המחשב, הבעיות עשויות להיות שונות לחלוטין מכיוון שהמבנה עצמו עשוי להיות גמיש למדי ומחוץ לטווח התדרים של רעידת האדמה. לכן, המבנה לא יכול לסבול כל נזק; עם זאת, תכולתו (ציוד לייצור שבבים) עלולה להיפגע קשות, וייצור השבבים עלול להיפגע. בהתאם למערך השבבים הספציפי המיוצר במתקן, הנזק הכלכלי הן לבעל המתקן והן לתעשייה כולה יכול להיות עצום.

שלוש דוגמאות אלה ממחישות מדוע יש לפתח אסטרטגיות תכנון עמידות עבור התשתית שלנו. כדי להגיע למטרה זו עלינו להבין הן את הקלט (תנועת הקרקע) והן את הפלט (תגובה מבנית). ניתן לטפל בבעיה זו רק באמצעות גישה אנליטית וניסוי משולבת. הראשון משתקף במשוואות המפורטות לעיל, בעוד שהאחרון יכול להיות מושג רק באמצעות העבודה הניסיונית שנעשתה באמצעות גישות שולחן מעין-סטטיות, פסאודו-דינמיות ומנערות שולחן.