Dynamique des structures

Source : Roberto Leon, département de génie Civil et environnemental, Virginia Tech, Blacksburg, VA

Il est rare de nos jours qu’une année entière se passe sans qu’un événement de tremblement de terre majeur des ravages quelque part dans le monde entier. Dans certains cas, comme le tremblement de terre 2005 de Banda Ache en Indonésie, les dommages impliqués de vastes régions géographiques et nombre de victimes dans les six chiffres. En général, le nombre et l’intensité des tremblements de terre n’augmente pas, cependant, augmente la vulnérabilité de l’environnement bâti. Avec l’urbanisation non réglementée autour des zones sismiquement actives, telles que la « ceinture de feu, » Circum-Pacifique mer passant en zone côtière pose de basse et l’augmentation des concentrations de production/distribution d’énergie et numérique/télécommunication nœuds critiques du réseau dans les zones vulnérables, il est clair que la conception parasismique est résilience communautaires clés pour le futur.

Conception de structures de résister à tremblement de terre a progressé considérablement au cours des 50 dernières années, principalement par le biais de travaux au Japon après le séisme de Niigata de 1964 et aux Etats-Unis après le séisme de San Fernando Valley de 1971. Le travail a avancé le long de trois voies parallèles : (a) travail expérimental visant à en développement techniques de construction améliorée pour minimiser les dégâts et pertes en vies humaines ; (b) des études analytiques basées sur des modèles matériels avancés géométriques et non linéaire ; et, (c) synthèse des résultats (a) et (b) dans les dispositions de code de conception qui améliorent la capacité des structures à résister aux charges inattendues.

La prospection sismique en laboratoire est souvent difficile et coûteuse. Essais sont effectués principalement à l’aide de trois techniques suivantes :

1. Tests de quasi statique (TVQ), où les parties d’une structure sont testés à l’aide d’appliqué lentement et prédéterminés de manière équivalente les déformations latérales avec conditions aux limites idéalisées. Cette technique est particulièrement utile pour évaluer les effets des détails structurels sur la capacité de résistance et de déformation des parties particulières des structures.
2. Tests de Pseudo-dynamique (PSDT), où les charges sont appliquées aussi lentement, mais les effets dynamiques sont pris en compte en résolvant les équations du mouvement en cours de test et en utilisant le test direct de rétroactions (principalement la rigidité instantanée) pour évaluer la rigidité réelle et caractéristiques de l’amortissement de la structure.
3. Secouer les tables, où les modèles réduits de structures complètes sont soumis pour entrer des requêtes à l’aide d’une commande hydraulique de base ou de la Fondation. Les tables de Shake représentent une plus fidèle technique de test, car la structure n’est pas restreint artificiellement, l’entrée est vrai mouvement et forces qui en résultent sont vraiment inertiel, comme on pourrait s’attendre à un véritable tremblement de terre. Cependant, les besoins en puissance sont énormes et seulement quelques-uns secouer tables capable de travailler à presque grandeur nature existent dans le monde entier. Globalement, il y a qu’une seule table de vibration grandes capables de réaliser des tests sur les structures à grande échelle, qui est la table de vibration à l’installation de E-Defense au Japon, construit après le séisme de Kobe de 1985.

Dans cette expérience, nous utiliserons une petite secousse table et modèle de structures afin d’étudier les caractéristiques du comportement dynamique de certains modèles structurels. C’est ces caractéristiques dynamiques, principalement la fréquence et l’amortissement, ainsi que la qualité des détails structurels et construction, qui font des structures plus ou moins vulnérable aux tremblements de terre.

Il y a une différence fondamentale entre l’habituel (poids propre) charges de gravité qui agissent sur une structure, qui sont quasi statique (c'est-à-dire, ils changent très lentement ou pas du tout avec le temps) et celles produites par les ouragans, les explosions et les tremblements de terre, qui sont extrêmement dynamiques par nature. Dans le cas des ouragans et autres charges dues au vent, il est possible de modéliser leurs effets sous des pressions statiques équivalentes en laboratoire que la fréquence des vents est très long par rapport à la fréquence naturelle fondamentale de la structure typique. Important d’exceptions à cette règle incluent des structures souples, tels que la longue travée haubanée et ponts suspendus, grands mâts et structures de turbine de vent, où la fréquence naturelle de la structure peut correspondre à celui des rafales de vent ou vent de droite. Dans le cas de tremblements de terre, les charges sont principalement inertiels que le sol se déplace, et la structure tend à rester encore. Dans ce cas, le chargement dépend de la masse réelle, la rigidité et l’amortissement de la structure, et les quantités d’intérêt sont les accélérations et vitesses de déplacements autour de la structure. Cette deuxième série de quantités est très difficile de reproduire avec précision en laboratoire si shake tables ne sont pas disponibles.

À l’aide de la physique fondamentale, comme la seconde loi de Newton, on peut simplifier le problème de l’équilibre d’une structure (par exemple un pont ou un cadre à poutre rigide), qui est soumis à des mouvements du sol (u,_g), à celle d’une seule masse de degrés de liberté (m) avec rigidité (k) et (c) caractéristiques de l’amortisseur. Les deux derniers peuvent être représentées par un ressort où la force est proportionnelle au déplacement (u) ainsi qu’un amortisseur dans lequel les forces sont proportionnelles à la vitesse (v) (Figure 1). Ces composants peuvent être combinés en parallèle ou série pour modéliser les différentes configurations structurelles.

Rigidité est définie comme la force nécessaire pour déformer la structure par un montant unitaire. Supposons que l'on charge un cantilever poutre avec une force connue (P) et de mesurer sa déformation élastique à l’extrémité (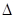). La rigidité est définie comme k = P /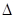. Pour le système de levier élastique simple illustré, k = /3EI³L, où L est la longueur du levier, I est son moment d’inertie, et E est le module de Young pour le matériel utilisé. Ensuite, imaginez ce qui se passe si on supprime la force tout à coup, ce qui permet le cantilever à vibrer. On attendra intuitivement à l’amplitude des vibrations de commencer à diminuer à chaque cycle. Ce phénomène s’appelle amortissement et se réfère à une série de mécanismes internes complexes, comme la friction, qui tendent à réduire les oscillations. La quantification de l’amortissement est décrite ultérieurement dans ce laboratoire, mais il est important de noter qu’à ce stade, pas beaucoup est connu au sujet de ces mécanismes du point de vue théorique ou pratique. Un concept utile consiste à visualiser le coefficient d’amortissement critique (c_cr), qui correspond au cas où le cantilever vient reposer après juste une oscillation complète.

Figure 1 : Modèle de système seul degré de liberté.

Écrire une équation d’équilibre horizontal des forces pour le système illustrée en Figure 1 conduit à :

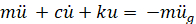(EQ. 1)

Si nous examinons un cas plus simple pour un moment, où nous pouvons ignorer parce que ses effets sont négligeables, et il n’y a aucune fonction de forçage externe d’amortissement, l’équation 1 devient l’équation différentielle homogène linéaire de second ordre :

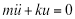(EQ. 2)

dont la solution est de la forme :

(EQ. 3)

Différencier les deux fois nous donnera :

(Équation 4)

Son remplacement par l’équation 4 dans l’équation 2, on obtient :

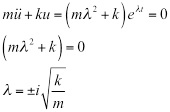(EQ. 5)

La solution générale est :

(Équation 6)

Où est la fréquence naturelle non amortie du système.

Si ce système est donné à un déplacement initial () et/ou une vitesse initiale (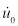), 6 de l’équation devient :

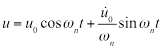(Équation 7)

Si on ajoute l’effet d’amortissement (c) et définir , la fréquence naturelle amortie du système devient et l’équivalent à l’équation 7 est :

(EQ. 8)

Dans le cas d’un déplacement initial u₀, la Figure 2 illustre le comportement pour plusieurs valeurs de .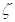

Figure 2 : Effet d’amortissement sur les vibrations libres : définition de l’amortissement critique (en haut) ; calcul de l’amortissement de décrément logarithmique (en bas).

Si dans la Figure 2, on définit , où u_n et u_{n +}1 sont le déplacement en cycles successifs, puis :

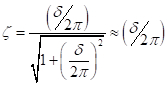(EQ. 9)

Revenir à l’équation 1, si le mouvement du sol est considéré comme la fonction sinusoïdale 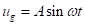, est l’analogue de l’équation 8 :

(Équation 10)

Où est le décalage de phase, et R_un est le facteur de réponse d’amplification, dont les parcelles sont illustrées à la Figure 3. La figure 3 montre que, pour de petites valeurs d’amortissement (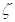 < 0,2), alors que la fréquence de la fonction de forçage approche la fréquence propre du système, la réponse du système devient instable, un phénomène qui est communément appelé résonance.

Figure 3 : Réponse de déplacement, de vitesse et d’accélération.

Dans cet atelier, nous étudierons expérimentalement les concepts et les dérivations derrière les équations 1 - 10 dans le cadre de la dynamique des structures à l’aide d’une table de vibration.

1. modèles

1. Tout d’abord construire plusieurs structures à l’aide de très minces, fortes, rectangulaires, T6011 poutres en aluminium, 1/32 po de largeur et ayant des longueurs différentes. Pour construire le premier modèle, insérez un porte-à-faux unique avec une longueur de 12 po à un bloc de bois très rigide. Placer une masse de 0,25 lb à l’extrémité du levier.
2. De même, construire des autres structures de modèle en attachant des poutres en porte-à-faux avec différentes longueurs pour le même bloc de bois rigide. Attacher un poids de 0,25 lb à l’extrémité de chaque cantilever.
3. Préparer deux autres spécimens simulant des structures d’armature simple avec colonnes flexibles et rigides planchers. Ceux-ci peuvent être construits de minces plaques d’acier et des diaphragmes de sol acrylique rigide. Une structure sera un seul étage et l’autre sera deux histoires. Les diaphragmes de plancher seront instrumentés avec accéléromètres.

2. les appareils

Pour ces manifestations une petite, il servira de table de vibration autocentreur, électriquement actionné, un degré de liberté. L’appareil se compose essentiellement d’une petite table métallique à cheval sur deux rails de guidage qui est déplacée par un moteur électrique. Le déplacement est contrôlé numériquement par un ordinateur qui peut entrée périodiques (ondes sinusoïdales) ou accélérations aléatoires (préprogrammée de tremblement de terre au sol histoires de temps d’accélération). Toute la commande est par le biais de logiciel propriétaire ou logiciel de type mulLink MatLab et Si. L’entrée en fonction de forçage peut être vérifiée en la comparant à la sortie d’un accéléromètre, attaché à la table.

3. mode opératoire

1. Soigneusement monter le modèle avec différents leviers à la table de vibration, à l’aide de boulons attachés à la base du modèle. Tourner sur la table de vibration et en utilisant le logiciel, augmentez lentement la fréquence jusqu'à obtention de la réponse maximale de la structure pour chaque cantilever. Notez que chaque cantilever pénètre par résonance à une fréquence particulière. Consigner dans un cahier de la valeur de cette fréquence. Continuer d’augmenter la fréquence jusqu'à ce que les déplacements de tous les leviers réduisent de manière significative.
2. Monter la structure du modèle d’un étage à la table de vibration et répéter la procédure. Balayez lentement sur des fréquences jusqu'à ce que la résonance est atteint. Réinitialiser le logiciel à une histoire de temps en accélération sol typique (1940 El Centro), pour montrer les mouvements aléatoires qui se produisent pendant un tremblement de terre.
3. Monter la structure de deux étages à la table de vibration et répéter la procédure. Notez que les deux fréquences naturelles se produisent dans ce cas.

Tout d’abord, déterminez la fréquence (ω) auquel le déplacement maximal s’est produite pour chaque modèle. La formule simple originale, nous l’avons vu, 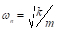, doit être modifié car la masse de la poutre elle-même (m_b = Wfaisceau/g), qui est distribué sur toute sa hauteur, n’est pas négligeable par rapport à la masse en haut (m = W _bloc/g). La masse équivalente pour le cas d’une poutre encastrée est (m + 0,23 m_b), où m est la masse en haut et en _b de la m est la masse distribuée de la poutre. La raideur k est donnée par l’inverse de la déformation (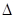) causé à la partie supérieure du levier par une force de l’unité :

(EQ. 11)

où L est la longueur de la poutre, E est le module d’élasticité et I est le moment d’inertie. J’ai est donnée par , où b est la largeur et h est l’épaisseur de la poutre. Ainsi, la fréquence naturelle circulaire d’une poutre encastrée, y compris son poids propre est :

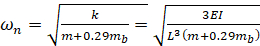(Eq.12)

Selon cette équation, les fréquences naturelles prédites sont calculés dans le tableau 1.

Nombre de faisceau	Longueur (en)	Largeur (en).	Épaisse. (en).	J’ai (in.4)	E (ksi)	Poids (lbs)	Poids de la poutre (lb.)	Masse effective (lbs-sec.2/en)	Fréquence propre (cycles par seconde)
1	12.0	1.002	0,124	1.59E-04	10200	0,147	0,149	4.70E-04	2.45
2	16,0	1,003	0,124	1.59E-04	10200	0,146	0.199	4.97E-04	1.55
3	20,0	1.002	0,125	1.63E-04	10200	0,146	0,251	5.28E-04	1.09
4	24,0	1,003	0,125	1.63E-04	10200	0,148	0,301	5.63E-04	0.80
5	28,0	1.001	0,125	1.63E-04	10200	0,144	0,350	5.82E-04	0,62
6	32,0	1.000	0,124	1.59E-04	10200	0,146	0,397	6.15E-04	0,49
7	36,0	1.002	0,126	1.67E-04	10200	0,147	0,455	6.52E-04	0,41
8	40,00	1.000	0,125	1.63E-04	10200	0,148	0.500	6.81E-04	0,34

Tableau 1 : Fréquences propres des poutres en porte-à-faux testés.

Le mesurées et les valeurs théoriques de la fréquence normale pour nos systèmes de modèles sont comparés dans le tableau 2. Les fréquences naturelles réelles ont été calculés par le déplacement soigneusement la poutre encastrée par 1 pouce et puis en regardant le déplacement vs temps de réponse. La comparaison ci-dessous sont faits en termes de périodes (T_d, s), comme elles ont été déterminées de T_d = u₀-u₁, comme illustré à la Figure 2(b). Cela nécessite des soins et patience pour obtenir des résultats fiables. Les manifestations montrées étaient uniquement destinées à donner une illustration globale le comportement de système.

Nombre de faisceau	Fréquence propre (cycles par seconde)	Période prévue (sec.)	Durée effective (sec.)	Erreur (%)
1	2.45	2,56	2.65	-3,33 %
2	1.55	4.06	4.23	-4,22 %
3	1.09	5.78	6.79	-17,52 %
4	0.80	7.84	8.04	-2,54 %
5	0,62	10.06	10.63	-5,70 %
6	0,49	12.79	13.04	-1,97 %
7	0,41	15.32	16.78	-9,50 %
8	0,34	18.59	20,56	-10,59 %

Le tableau 2. Comparaison des résultats.

Les différences tiennent principalement au fait que les poutres ne sont pas fixés de façon rigide à la base en bois, et la flexibilité supplémentaire à la base augmente la durée de la structure. Une autre source d’erreur est que l’amortissement ne faisaient pas dans les calculs, car l’amortissement est très difficile à mesurer et à amplitude dépendant.

Ensuite, chacun du déplacement vs temps, tirer le maximum de valeur pour chaque fréquence et tracer l’ampleur du déplacement par rapport à la fréquence normalisée comme ça à la Figure 3. Un exemple est illustré à la Figure 4, où nous avons normalisé de fréquence par rapport à la première fréquence naturelle (faisceau numéro 1) et tracer le déplacement maximal de cette poutre lorsque la table de vibration a été soumise à une déformation variable sinusoïdale d’amplitude de 1 po.

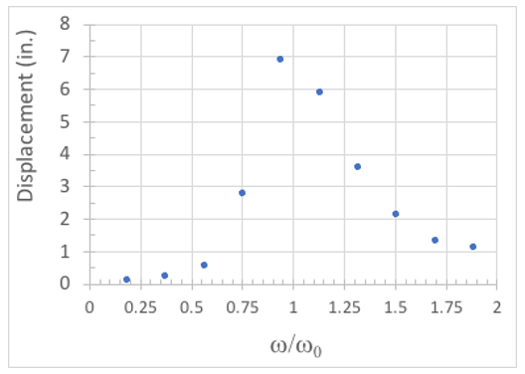
Figure 4 : Déformation du faisceau #1 vs fréquence normalisée table.

Au début, lorsque le ratio ω ω/_n est petit, il n’est pas réponse bien que l’énergie d’entrée de la requête de table n’excite pas le modèle. Comme ω/ω_n 1 s’approche, il y a une augmentation très significative dans la réponse, avec les déformations deviennent assez grandes. La réponse maximale est atteinte lorsque ω ω/_n est très proche de 1. Comme la fréquence normalisée augmente au delà de ω/ω_n = 1, la réponse dynamique commence à mourir vers le bas ; Lorsque ω/ω_n devient grand nous sommes dans une situation où la charge est appliquée très lentement en ce qui concerne la fréquence naturelle de la structure, et la déformation devienne égale à celle d’une charge statique appliquée.

Ces expériences vise principalement à montrer les changements dans le comportement qualitatif, comme indiqué dans les manifestations pour les structures de deux châssis. Obtenir des résultats semblables à ceux dans les Figures 3 et 4 nécessite beaucoup de soin et de la patience comme sources de friction et semblables affecteront le montant d’amortissement et donc décaler les courbes semblables à ceux de la Figure 3(c) à gauche ou à droite comme le réel amortie fréquence, 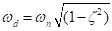, modifications.

Dans cette expérience, la fréquence et l’amortissement d’un système en porte-à-faux simple ont été mesurées à l’aide de tables de secousse. Bien que le contenu de la fréquence d’un séisme est aléatoire et couvre une large bande de fréquences, les spectres de fréquence peuvent être développées en traduisant l’histoire de temps d’accélération dans le domaine des fréquences grâce à l’utilisation des transformées de Fourier. Si les fréquences prédominantes des mouvements du sol correspond à celle de la structure, il est probable que la structure fera l’objet d’importants déplacements et par conséquent exposée à beaucoup de dégâts ou même l’effondrement. Conception parasismique ressemble à la forme de niveaux attendus d’accélération, un tremblement de terre à un endroit donné, basé sur des documents historiques, distance à la source du tremblement de terre, le type et la taille de la source du tremblement de terre, et l’atténuation de la surface et le corps des ondes pour déterminer un niveau raisonnable de l’accélération à utiliser pour la conception.

Ce que le grand public souvent ne réalise pas est que les dispositions actuelles de conception parasismique sont utilisés exclusivement pour minimiser la probabilité d’effondrement et de perte de vie dans le cas où un séisme maximal prévisible se produit à un niveau acceptable (environ 5 à 10 % dans la plupart cas). Alors que les concepts de structures pour obtenir bas probabilités de défaillance sont possibles, ils commencent à devenir rentable. Minimiser les pertes et améliorer la résilience après un tel événement explicitement ne constituent pas aujourd'hui, bien que ces considérations sont devenues plus fréquentes, comme autant de fois le contenu d’un bâtiment et ses fonctionnalités peuvent être beaucoup plus importante que son innocuité. Prenons par exemple le cas d’une centrale nucléaire (comme Fukushima dans le grand séisme de Kanto de 2011), un immeuble résidentiel de dix étages à Los Angeles ou une puce d’ordinateur fabrication installation dans la Silicon Valley et de leur exposition et la vulnérabilité sismique événements.

Dans le cas de la centrale nucléaire, il peut être souhaitable pour concevoir la structure pour réduire au minimum tout dommage compte tenu du fait que la conséquence de défaillance même minime peut être très lourd de conséquences. Dans ce cas, nous devrions essayer de localiser cet établissement aussi loin que possible des sources de tremblement de terre pour minimiser l’exposition, parce que réduire la vulnérabilité au niveau désiré est très difficile et coûteux. La réalité est qu’il est trop coûteux de le faire étant donné le désir du public pour éviter non seulement un incident de Fukushima-type, mais aussi encore plus limité un, comme la catastrophe nucléaire de Three Mile Island.

Pour multi-l’histoire bâtiment à Los Angeles, il est plus difficile minimiser l’exposition parce qu’un vaste réseau de failles sismiques avec des périodes de retour un peu inconnus se trouve à proximité, notamment la faille de San Andreas. Dans ce cas, l’accent doit être sur une conception robuste et les détails afin de minimiser la vulnérabilité de l’ouvrage ; les propriétaires des résidences devraient être conscients qu’ils prennent un risque important en cas de tremblement de terre. Ils ne doivent pas s’attendre du bâtiment s’effondrer, mais le bâtiment peut être une perte totale si le tremblement de terre est d’une grande assez grandeur.

Pour l’usine de puce d’ordinateur, les problèmes peut être complètement différentes parce que la structure elle-même peut être assez souple et à l’extérieur de la bande passante du tremblement de terre. Ainsi, la structure ne peut-être pas souffrir aucun dommage ; Toutefois, son contenu (matériel de fabrication de puce) peut-être être gravement endommagés, et production de copeaux pourrait être perturbée. Selon l’ensemble spécifique de puces en cours de fabrication à l’installation, les dommages économiques tant pour le propriétaire de l’installation et à l’industrie dans son ensemble peuvent être énorme.

Ces trois exemples illustrent la raison pour laquelle on a besoin élaborer des stratégies de conception résiliente pour notre infrastructure. Pour atteindre cet objectif, que nous devons comprendre l’entrée (mouvement du sol) et la sortie (réponse). Cette question peut seulement être traitée grâce à une approche analytique et expérimentale. Le premier se reflète dans les équations ci-dessus, alors que ce dernier ne peut être atteint grâce au travail expérimental effectué par le biais de quasi statique, Pseudo-dynamiques et secouer les approches de la table.