Analyse einer Düse: Variationen in Machzahl und Druck entlang einer konvergierenden und einer konvergierend-divergierenden Düse

Quelle: Shreyas Narsipur, Maschinenbau und Luft- und Raumfahrttechnik, North Carolina State University, Raleigh, NC

Eine Düse ist ein Gerät, das aufgrund seines unterschiedlichen Querschnitts häufig verwendet wird, um den Fluss zu beschleunigen oder zu verlangsamen. Düsen sind weit verbreitet in Luft- und Raumfahrt-Antriebssystemen verwendet. Bei Raketen wird das aus der Kammer ausgestoßene Treibmittel durch eine Düse beschleunigt, um eine Reaktionskraft zu erzeugen, die das System antreibt. In Strahltriebwerken wird eine Düse verwendet, um Energie aus einer Hochdruckquelle in kinetische Energie des Auspuffs umzuwandeln, um Schub zu erzeugen. Das isentrope Modell entlang der Düse ist ausreichend für eine Erstordnungsanalyse, da der Durchfluss in einer Düse sehr schnell (und damit adiabatisch zu einer ersten Annäherung) mit sehr geringen Reibungsverlusten ist (weil der Durchfluss fast eindimensional mit einem günstigen Druck ist Gradient, außer wenn sich Schockwellen bilden und Düsen relativ kurz sind).

In diesem Experiment werden zwei Düsentypen auf einem Düsenprüfstand montiert, und ein Druckfluss wird mit einer Druckluftquelle erzeugt. Die Düsen werden für verschiedene Rückdruckeinstellungen ausgeführt, um den internen Fluss in den Düsen unter unterschiedlichen Strömungsbedingungen zu analysieren, die verschiedenen Strömungsregime zu identifizieren und die Daten mit theoretischen Vorhersagen zu vergleichen.

Eine Düse beginnt an der Stelle, an der der Kammerdurchmesser zu abnehmen beginnt. Es gibt zwei Hauptarten von Düsen: die konvergierende Düse und die konvergierende-divergierende Düse. Eine der regierenden isentropen Beziehungen zwischen Mach-Zahl (M), Düsenbereich (A) undGeschwindigkeit (u) wird durch die folgendeGleichung dargestellt:

(1)

wobei u die Geschwindigkeit, A der Düsenbereich und M die Mach-Zahl ist. Basierend auf Gleichung 2,

1. Bei M = 0 ist der Durchfluss statisch, d.h. es besteht eine Nicht-Flow-Bedingung
2. Bei 0 < M < 1 wird bei abnehmender Fläche eine proportionale Zunahme der Strömungsgeschwindigkeit beobachtet
3. Bei M 1 führt jede Flächenerhöhung zu einer proportionalen Erhöhung der Geschwindigkeit

Konvergierende Düsen, wie in Abbildung 1dargestellt, sind Rohre mit einem Bereich, der vom Düseneingang zum Ausgang (oder Hals) der Düse abnimmt. Wenn der Düsenbereich abnimmt, nimmt die Strömungsgeschwindigkeit zu, wobei die maximale Strömungsgeschwindigkeit an der Düsenkehle auftritt. Wenn die Einlassströmungsgeschwindigkeit erhöht wird, steigt die Strömungsgeschwindigkeit an der Düsenkehle weiter an, bis sie Mach 1 erreicht. An diesem Punkt wird der Fluss an der Kehle erstickt, was bedeutet, dass jede weitere Erhöhung der Einlassströmungsgeschwindigkeit die Strömungsgeschwindigkeit am Hals nicht erhöht. Aus diesem Grund werden konvergierende Düsen verwendet, um Flüssigkeiten im Unterschall-Flussregime allein zu beschleunigen und können häufig auf allen kommerziellen Jets (mit Ausnahme der Eintracht) gefunden werden, da sie mit Unterschallgeschwindigkeiten reisen.

Abbildung 1. Schemat einer konvergierenden Düse. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

Für Fahrzeuge wie Raketen und Militärflugzeuge, die mit und über der Schallgeschwindigkeit fahren müssen, wird eine konvergierende, divergierende Düse verwendet, wie in Abbildung 2dargestellt. In einer konvergierenden, divergierenden Düse folgt auf den konvergierenden Abschnitt ein divergierender Düsenabschnitt und ist so ausgelegt, dass der Durchfluss an der Kehle des konvergierenden Abschnitts erstickt wird, wodurch die Massendurchflussrate im System fixiert wird. Der Fluss wird dann entropisch erweitert, um Überschall-Mach-Zahlen im divergierenden Abschnitt zu erreichen. Die im Divergenzabschnitt eingestellten Überschallfungsgeschwindigkeiten sind eine Funktion der Düsenflächenverhältnisse nach der Kehle. Basierend auf dem Design der konvergierenden, divergierenden Düse kann die Strömungsgeschwindigkeit nach dem Düsenhals entweder: (i) auf Unterschallgeschwindigkeiten abnehmen, (ii) Überschall werden, einen normalen Schock verursachen und dann auf Unterschallgeschwindigkeiten am Düsenausgang abnehmen, oder (iii) überschall über den divergierenden Abschnitt bleiben. Die Schubmenge, die von der Düse erzeugt wird, hängt von der Austrittsgeschwindigkeit und dem Druck und der Massendurchflussrate durch die Düse ab.

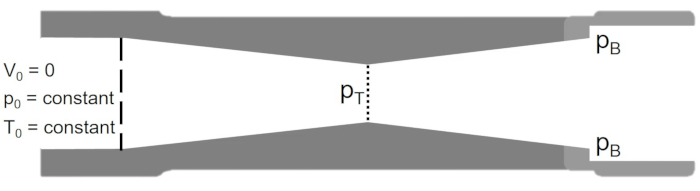
Abbildung 2. Schemat einer konvergierenden, divergierenden Düse. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

Der Gegendruck (p_B) ist der Antriebsfaktor, der die Strömungsbedingung in der Düse bestimmt. Wenn der Stagnationsdruck, p_O = p_B, gibt es keinen Fluss durch die Düse. Wenn p_B reduziert wird, erhöht sich die Mach-Zahl an der Kehle (p_T) bis der Durchfluss erstickt ist (M_T = 1). Der Zustand, in dem erstickter Fluss auftritt, kann mit der isentropen Beziehung berechnet werden:

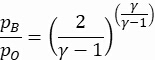(2)

wobei das spezifische Wärmeverhältnis der Flüssigkeit ist. Durch die Substitution von n = 1,4 (spezifisches Wärmeverhältnis für Trockenluft) in Gleichung 2 erhalten wir ein Gegendruckverhältnis von:

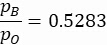(3)

Gleichung 3 definiert die Grenze zwischen den nicht erstickten und erstickten Strömungsregimen. Wenn der Fluss erstickt wird, erhöht sich die Mach-Zahl nicht mehr und ist auf M = 1begrenzt.

Bei einer konvergierenden Düse entspricht der Ausgang der Düse der Düsenkehle (wie in Abbildung 1zu sehen ); Daher überschreitet die Mach-Nummer direkt am Ausgang 1 nicht, d.h. der Fluss wird nie überschall. Sobald der Durchfluss die Düse verlässt, erfährt er eine Ausdehnung, aufgrund der plötzlichen Zunahme der Fläche, die zu (unkontrollierten) Überschallfflussgeschwindigkeiten führen könnte.

Basierend auf Abbildung 3sind die folgenden Strömungsbedingungen, die in einer konvergierenden Düse beobachtet werden können:

1. Keine Strömungsbedingung, bei der der Gegendruck dem Gesamtdruck entspricht.
2. Unterschallfluss, bei dem sich der Durchfluss beschleunigt, wenn die Fläche abnimmt und der Druck sinkt.
3. Unterschallfluss, wo es eine deutlich höhere Beschleunigung und Druckabfall gibt.
4. Erstickter Fluss, bei dem jeder Druckabfall den Durchfluss nicht beschleunigt.
5. Erstickter Fluss, bei dem sich der Fluss nach dem Düsenausgang ausdehnt (als nicht-isentrop).

Abbildung 3. Strömungsbedingungen und -regime in einer konvergierenden Düse (theoretische Vorhersagen). Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

Der Massenflussparameter (MFP) ist eine Variable, die die Geschwindigkeit bestimmt, mit der die Masse durch die Düse fließt, und wird durch die Gleichung angegeben:

(4)

Hier ist die Massendurchflussrate durch die Düse, T_O ist die Stagnationstemperatur, und A_T ist der Bereich der Kehle, die, im Falle der konvergierenden Düse, gleich dem Bereich am Düsenausgang ist, A_E . Wie in Abbildung 3beobachtet, nimmt das MFP bis zum erstickten Fluss weiter zu. Sobald der Durchfluss erstickt ist, wird der Massendurchfluss festgelegt, und das MFP bleibt eine Konstante für abnehmende Gegendruckverhältnisse.

Um kontrollierte Überschallströme in einer Düse zu erreichen, muss nach der Kehle einer konvergierenden Düse ein divergierender Abschnitt eingeführt werden, wie in Abbildung 2dargestellt. Sobald der Fluss an der Kehle einer konvergierenden, divergierenden Düse erstickt wird (basierend auf Gleichung 3), können drei mögliche Strömungsbedingungen auftreten: unterschallisanter isentropischer Fluss (der Fluss verlangsamt sich nach dem erstickten Zustand), Überschall-nicht-isentroper Fluss (wo die Der Fluss beschleunigt sich supersonisch, bildet eine Schockwelle - eine dünne Region von koalierten Molekülen, die sich bis zu einem bestimmten Punkt auf der Düse normal bildet und eine plötzliche Veränderung der Strömungsbedingungen verursacht, die allgemein als normaler Schock bezeichnet wird - und verlangsamt subsonisch nach dem Oder Überschall-Isentropenstrom (wo sich der Fluss nach dem erstickten Zustand supersonisch beschleunigt). Abbildung 4 zeigt die folgenden sieben Profile im Positions-/Druckverhältnisdiagramm. Beachten Sie, dass die erste vertikale gestrichelte Linie auf der linken Seite des p/p_O im Vergleich zur Entfernung entlang des Düsendiagramms die Position der Kehle ist, die zweite vertikale gestrichelte Linie die Position des Düsenausgangs ist und die horizontal gestrichelte Linie den erstickten Zustand markiert.

1. Unterschallfluss, der nie erstickten Zustand erreicht.
2. Unterschallfluss, der erstickten Zustand erreicht, aber keine Überschallgeschwindigkeiten erreicht (als isentrop betrachtet).
3. Unterschallfluss, der erstickten Zustand erreicht, wobei der resultierende Überschallstrom einen normalen Schock bildet, der dann eine unterschallende Verzögerung erfährt. Hier bewirkt der normale Schock einen plötzlichen Geschwindigkeitsabfall und einen Anstieg des Gegendrucks, wie der plötzliche Anstieg der p/p_Ozeigt.
4. Unterschallfluss, der erstickten Zustand erreicht, mit dem resultierenden Überschallstrom bilden einen normalen Schock nach der Düse (als isentrop in der Düse).
5. Überdehnte Strömung – der Druck am Düsenausgang ist niedriger als der Umgebungsdruck, wodurch der Jet, der die Düse verlässt, sehr instabil ist und große Druck- und Geschwindigkeitsschwankungen aufweist, wenn er flussabwärts fährt.
6. Fluss nach dem erstickten Zustand ist Überschall durch die Düse, und es bildet sich kein Schock.
7. Unterdausbausmenge – der Druck am Düsenausgang ist höher als der Umgebungsdruck und führt zu ähnlichen Effekten wie ein überdehner Durchfluss.

Abbildung 4. Strömungsbedingungen und -regime in einer konvergierenden, divergierenden Düse (theoretische Vorhersagen). Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

In dieser Demonstration wurde ein Düsenprüfstand verwendet, der aus einer Druckluftquelle bestand, die Hochdruckluft durch die getesteten Düsen kanalisiert, wie in Abbildung 5dargestellt. Der Durchflussdruck reicht von 0 - 120 psi und wird über ein mechanisches Ventil gesteuert. Während die Drücke mit einem externen Sensor gemessen werden, werden die Massendurchflussraten in der Düse durch ein Paar Rotameter gemessen, die direkt vor dem Auspuff des Düsenprüfstandes platziert werden.

Abbildung 5. Düsenprüfstand. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

1. Messung des Axialdrucks in konvergierenden und konvergierenden Düsen

1. Montieren Sie die konvergierende Düse in der Mitte des Düsenprüfstandes, wie in Abbildung 5dargestellt. Der 2D-Abschnitt für die konvergierende Düse mit Etiketten für die Druckhähne ist in Abbildung 6dargestellt.

Abbildung 6. Geometrie der konvergierenden Düse. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

2. Verbinden Sie die 10 statischen Druckanschlüsse und den Stagnationsdruckanschluss mit flexiblen Hochdruck-PVC-Rohren an das Druckmesssystem.
3. Schließen Sie das Druckmesssystem an die grafische Software-Schnittstelle an, um Druckdaten in Echtzeit zu lesen.
4. Nehmen Sie den Null-/Nicht-Flow-Bedingungswert.
5. Öffnen Sie das mechanische Durchflussregelventil, um den Luftstrom zu starten.
6. Drehen Sie das Ventil, um den Durchfluss anzupassen, um ein Gegendruckverhältnis (p_B/p_O) von 0,9 zu erhalten. Beachten Sie, dass der Gegendruck sowohl für die konvergierenden als auch für die konvergierenden Divergenzen den Druckdaten entspricht, die aus Port 10 ausgelesen werden.
7. Zeichnen Sie die Daten auf, die Tabelle 1 entsprechen.
8. Verringern Sie das Gegendruckverhältnis in Schritten von 0,1 bis p_B/p_O = 0,1 Wiederholungsschritt 7 für jede Einstellung. Wiederholen Sie außerdem Schritt 7 für ein p_B/p_O = 0,5283, um Strömungsdaten bei der theoretisch erstickten Strömungsbedingung zu erfassen.
9. Ersetzen Sie die konvergierende Düse durch die konvergierende,divergierende Düse und wiederholen Sie die Schritte 1.2 - 1.8. Der 2D-Abschnitt für die konvergierende Düse mit Etiketten für die Druckhähne ist in Abbildung 7dargestellt.
10. Trennen Sie nach Abschluss der Tests alle Systeme und demontieren Sie den Düsenprüfstand.

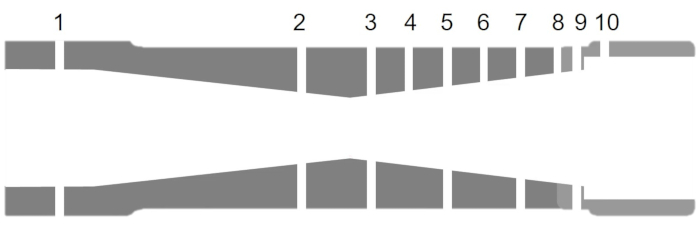
Abbildung 7. Geometrie der konvergierenden, divergierenden Düse. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

Tabelle 1. Daten, die für das Düsenexperiment gesammelt wurden.

Tippnummer	Axiale Position des Taps (in)	Düsenflächenverhältnis (A/Ai)	Pstatisch (psi)	Po (psi)	masse Durchflussrate (Schnecken/s)	Patm (psi)	To (°F)
Abbildung 6/7	Tabelle 2	Tabelle 2	Messdruck	messen druck	Rotameter	Messdruck	Temperatursensor

Tabelle 2. Düsengeometriedaten.

Tippnummer	Konvergierende Düse		Konvergierende-Divergierende Düse
	Axiale Position des Taps (in)	Düsenflächenverhältnis (A/Ai)	Axiale Position des Taps (in)	Düsenflächenverhältnis (A/Ai)
1	0	60.14	0	60.14
2	1	51.379	4.5	6.093
3	2	35.914	6.5	1
4	3	23.218	6.9075	1.053
5	4	13.275	7.3795	1.222
6	5	6.094	7.8515	1.403
7	5.5	3.54	8.3235	1.595
8	6	1.672	8.7955	1.802
9	6.5	1	9.2675	2.02
10	7	60.041	9.5	60.041

Bei der Analyse wurden folgende Konstanten verwendet: spezifische Wärme der trockenen Luft, n: 1,4; Referenzdüsenbereich, A_i = 0,0491 in², und Standard-Atmosphärendruck, P_atm = 14,1 psi. Die Abbildungen 8 und 9 zeigen die Variation des Druckverhältnisses und der Mach-Zahl über die Länge der Düse (normalisiert basierend auf der Gesamtdüsenlänge) für verschiedene Gegendruckeinstellungen für die konvergierenden bzw. konvergierenden Düsen. Der Massendurchflussparameter im Vergleich zum Gegendruckverhältnis wird ebenfalls für beide Düsen geplottet und untersucht.

Ab Abbildung 8beobachten wir, dass bei abnehmendem p _{B/pO-Verhältnis} (bis 0,5283) der Fluss an jedem Teil der Düse unterschallist und mit abnehmender Fläche zunimmt. Bei und unter p_B/p_O = 0,5283 überschreitet die Mach-Zahl an der Kehle (normalisierter Düsenabstand = 0,93) einen nicht. Dies zeigt deutlich, dass der Fluss an der Kehle erstickt ist. Jenseits des Kehl-Düsen-Ausgangs gibt es eine unkontrollierte Ausdehnung des Flusses, was zu Überschall-Mach-Nummern führt. Die gesamten Trends in der p/p_O-Verteilung entsprechen den theoretischen Trends aus Abbildung 3. Die Trends im MFP folgen theoretischen Ergebnissen bis p_B/p_O = 0,6, beginnen aber zu verringern, anstatt für niedrigere Werte der Gegendruckverhältnisse zu plateauing. Da der Durchfluss erstickt ist, sollte das MFP konstant sein. Basierend auf der Position des Wasserhahns, der den Kehlkopfdruck misst (Tipp 9, Abbildung 6), sehen wir jedoch, dass die Messungen leicht vor der echten Düsenkehle durchgeführt werden, was wiederum zu einer falschen Messung des MFPführt.

Bei der konvergierenden, divergierenden Düse (Abbildung 9) wird der Unterschallfluss beobachtet, bis p/p_O am Hals (normalisierter Düsenabstand = 0,68) 0,5283 entspricht (gewürgter Durchflusszustand). Die weitere Reduktion von p_B/p_O zeigt drei unterschiedliche Muster:
a. Muster 1 - Flow erreicht erstickten Zustand an der Kehle und verlangsamt subsonisch im divergierenden Abschnitt (0,8 < p_B/p_O < 0,7).
b. Muster 2 - Flow beschleunigt supersonisch über die Kehle hinaus, bildet einen Schock im divergierenden Abschnitt und verlangsamt (in einigen Fällen auf Unterschallgeschwindigkeiten) für 0,7 < p_B/p_O < 0,3.
c. Muster 3 - Der Fluss beschleunigt weiterhin supersonisch für den gesamten divergierenden Abschnitt für p_B/p_O-Werte unter 0,3.

Das MFP steigt mit abnehmenden Gegendruckverhältnissen, Spitzen bei p_B/p_O = 0,5 und beginnt zu sinken, anstatt konstant zu bleiben, wie von der Theorie vorhergesagt.

Abbildung 8. Ergebnisse für die konvergierende Düse (von oben rechts, im Uhrzeigersinn) Variation des Druckverhältnisses über die Düse; Variation der Mach-Zahl über die Düse; und Variation des Massenpflugparameters mit Gegendruckverhältnis. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

Düsen werden häufig in Flugzeugen und Raketenantrieben verwendet, da sie eine einfache und effektive Methode bieten, um den Fluss in begrenzten Entfernungen zu beschleunigen. Um Düsen für eine bestimmte Anwendung zu entwerfen, ist ein Verständnis des Strömungsverhaltens und der Faktoren, die dieses Verhalten für eine Reihe von Strömungsbedingungen beeinflussen, für die Entwicklung effizienter Antriebssysteme unerlässlich. In dieser Demonstration wurden die konvergierenden und konvergierenden, divergierenden Düsen - zwei der häufigsten Düsentypen, die in Luft- und Raumfahrtanwendungen verwendet werden - mit einem Düsenprüfstand getestet. Die Druck- und Mach-Zahlenschwankungen zwischen den beiden Düsen wurden für eine Vielzahl von Strömungsbedingungen untersucht.

Die Ergebnisse der konvergierenden Düsentests zeigten, dass die maximale Grenze, bis zu der der Durchfluss beschleunigt werden kann, M = 1 ist, bei dem der Punktfluss an der Düsenkehle erstickt wird. Sobald der Durchfluss erstickt ist, hat jede Erhöhung der Einlass-Flussgeschwindigkeit die Strömungsgeschwindigkeit am Hals/Ausgang nicht auf Überschallgeschwindigkeiterhöht. Die Analyse der konvergierenden, divergierenden Düse gibt Einen Einblick, wie Überschallströmungsgeschwindigkeiten erreicht werden können, sobald der Fluss an der Kehle erstickt wird. Wir beobachteten auch drei Arten von Strömungen, die nach der erstickten Kehle je nach dem Gegendruckverhältnis des Durchflusses erhalten werden können. Ein Vergleich der Drucktrends sowohl für die konvergierenden als auch für die konvergierenden Typdüsen mit theoretischen Ergebnissen war ausgezeichnet. Die experimentellen Ergebnisse zeigten jedoch, dass der Massenflussparameter für niedrigere Werte des Gegendruckverhältnisses abnimmt, anstatt sich zu veranlassen, sobald der Maximalwert erreicht wurde, wie von der Theorie vorhergesagt.

Abbildung 9. Ergebnisse für die konvergierende-divergierende Düse (von oben rechts, im Uhrzeigersinn) Variation des Druckverhältnisses über die Düse; Variation der Mach-Zahl über die Düse; und Variation des Massenpflugparameters mit Gegendruckverhältnis. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.