Method Article
Вычислительное моделирование нейронов сетчатки для исследования зрительных протезов - Фундаментальные подходы
В этой статье
Резюме
Мы суммируем рабочий процесс для вычислительного моделирования поведения нейрона сетчатки в ответ на электрическую стимуляцию. Вычислительная модель универсальна и включает в себя этапы автоматизации, которые полезны для моделирования ряда физиологических сценариев и прогнозирования результатов будущих исследований in vivo / in vitro .
Аннотация
Вычислительное моделирование становится все более важным методом в нейронной инженерии из-за его способности предсказывать поведение систем in vivo и in vitro . Это имеет ключевое преимущество минимизации количества животных, необходимых в данном исследовании, предоставляя часто очень точное прогнозирование физиологических результатов. В области визуального протезирования вычислительное моделирование имеет множество практических применений, включая информирование о конструкции имплантируемой электродной решетки и прогнозирование визуальных восприятий, которые могут быть вызваны доставкой электрических импульсов от указанного массива. Некоторые модели, описанные в литературе, сочетают трехмерную (3D) морфологию для вычисления электрического поля и кабельную модель интересующего нейрона или нейронной сети. Чтобы повысить доступность этого двухэтапного метода для исследователей, которые могут иметь ограниченный предыдущий опыт в вычислительном моделировании, мы предоставляем видео фундаментальных подходов, которые должны быть приняты для построения вычислительной модели и использования ее для прогнозирования физиологических и психофизических результатов протоколов стимуляции, развернутых через зрительный протез. Руководство включает в себя шаги по построению 3D-модели в программном обеспечении для конечно-элементного моделирования (FEM), построение модели ганглиозных клеток сетчатки в многокамерном вычислительном программном обеспечении нейронов с последующим объединением двух. Программное обеспечение для моделирования конечных элементов для численного решения физических уравнений будет использоваться для решения распределения электрического поля при электрической стимуляции ткани. Затем было использовано специализированное программное обеспечение для моделирования электрической активности нейронной клетки или сети. Чтобы следовать этому руководству, потребуется знакомство с принципом работы нейропротеза, а также нейрофизиологическими концепциями (например, механизмом потенциала действия и пониманием модели Ходжкина-Хаксли).
Введение
Визуальные нейропротезы представляют собой группу устройств, которые доставляют стимуляцию (электрическую, световую и т. Д.) Нервным клеткам в зрительном пути для создания фосфенов или ощущения видения света. Это стратегия лечения, которая используется в клинике в течение почти десятилетия для людей с постоянной слепотой, вызванной дегенеративными заболеваниями сетчатки. Как правило, полная система будет включать в себя внешнюю камеру, которая захватывает визуальную информацию вокруг пользователя, блок питания и вычислительный блок для обработки и преобразования изображения в серию электрических импульсов и имплантированную электродную решетку, которая взаимодействует с нервной тканью и доставляет электрические импульсы к нервным клеткам. Принцип работы позволяет размещать визуальный нейропротез в разных местах вдоль зрительного пути от сетчатки до зрительной коры, если он находится ниже по течению от поврежденной ткани. Большинство современных исследований в области зрительных нейропротезов сосредоточены на повышении эффективности стимуляции и улучшении пространственной остроты для обеспечения более естественного зрения.
В усилиях по повышению эффективности стимуляции вычислительное моделирование было экономически эффективным и эффективным методом для проверки конструкции протеза и моделирования его визуального результата. Вычислительное моделирование в этой области приобрело популярность с 1999 года, когда Гринберг1 смоделировал реакцию ганглиозной клетки сетчатки на внеклеточные электрические стимулы. С тех пор вычислительное моделирование стало использоваться для оптимизации параметров электрического импульса 2,3 или геометрического проектирования электрода 4,5. Несмотря на различия в сложности и исследовательских вопросах, эти модели работают, определяя распределение электрического напряжения в среде (например, нервной ткани) и оценивая электрический ответ, который нейроны в окрестностях будут производить из-за электрического напряжения.
Распределение электрического напряжения в проводнике можно найти, решив уравнения Пуассона6 во всех местах:
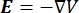
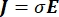
где E — электрическое поле, V — электрический потенциал, J — плотность тока, а σ — электропроводность. В  уравнении указывает оператор градиента. В случае стационарного тока на модель накладываются следующие граничные условия:
уравнении указывает оператор градиента. В случае стационарного тока на модель накладываются следующие граничные условия:


где n — нормаль поверхности, Ω — границу, а I0 — конкретный ток. Вместе они создают электрическую изоляцию на внешних границах и создают источник тока для выбранной границы. Если предположить монополярный точечный источник в однородной среде с изотропной проводимостью, то внеклеточный электрический потенциал в произвольном месте может быть рассчитан на7:

где Ie — ток и — расстояние между электродом и точкой измерения. Когда среда неоднородна или анизотропна, или электродная решетка имеет несколько электродов, вычислительный набор для численного решения уравнений может быть удобным. Конечно-элементное программное обеспечение для моделирования6 разбивает объемный проводник на небольшие участки, известные как «элементы». Элементы взаимосвязаны друг с другом так, что эффекты изменения одного элемента влияют на изменение в других, и это решает физические уравнения, которые служат для описания этих элементов. С увеличением вычислительной скорости современных компьютеров этот процесс может быть завершен в течение нескольких секунд. Как только электрический потенциал рассчитан, можно оценить электрический отклик нейрона.
Нейрон посылает и получает информацию в виде электрических сигналов. Такие сигналы бывают двух форм - градуированные потенциалы и потенциалы действия. Градуированные потенциалы представляют собой временные изменения мембранного потенциала, при которых напряжение через мембрану становится более положительным (деполяризация) или отрицательным (гиперполяризация). Градуированные потенциалы обычно имеют локализованные эффекты. В клетках, которые их производят, потенциалы действия — это реакции «все или ничего», которые могут перемещаться на большие расстояния по длине аксона. Как градуированные, так и активные потенциалы чувствительны как к электрической, так и к химической среде. Всплеск потенциала действия может быть произведен различными типами нейрональных клеток, включая ганглиозные клетки сетчатки, когда пороговый трансмембранный потенциал пересекается. Всплеск и распространение потенциала действия затем вызывают синаптическую передачу сигналов нисходящим нейронам. Нейрон может быть смоделирован как кабель, который разделен на цилиндрические сегменты, где каждый сегмент имеет емкость и сопротивление из-за липидной двухслойной мембраны8. Нейронная вычислительная программа9 может оценить электрическую активность электрически возбудимой клетки, дискретизируя клетку на несколько отсеков и решая математическую модель10:
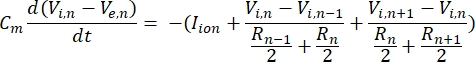
В этом уравнении Cm— емкость мембраны, Ve,n — внеклеточный потенциал в узле n, Vi,n — внутриклеточный потенциал в узле n, Rn— внутриклеточное (продольное) сопротивление в узле n, а I-ион — ионный ток, проходящий через ионные каналы в узле n. Значения V из модели FEM реализованы как Ve,n для всех узлов в нейроне, когда стимуляция активна.
Трансмембранные токи из ионных каналов могут быть смоделированы с использованием формул Ходжкина-Хаксли11:
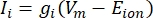
где gi — удельная проводимость канала, Vm — трансмембранный потенциал (Vi,n — Ve,n), а E-ион — обратный потенциал ионного канала. Для каналов с напряжением, таких как Канал Na, вводятся безразмерные параметры, m и h, которые описывают вероятность открытия или закрытия каналов:
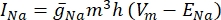
где  — максимальная мембранная проводимость для конкретного ионного канала, а значения параметров m и h определяются дифференциальными уравнениями:
— максимальная мембранная проводимость для конкретного ионного канала, а значения параметров m и h определяются дифференциальными уравнениями:

где αx и βx являются зависимыми от напряжения функциями, определяющими константы скорости ионного канала. Как правило, они принимают форму:

Значения параметров в этих уравнениях, включая максимальную проводимость, а также константы A, B, C и D, обычно находились из эмпирических измерений.
С помощью этих строительных блоков можно построить модели различной сложности, выполнив описанные шаги. Программное обеспечение FEM полезно, когда уравнение Пуассона не может быть решено аналитически, например, в случае неоднородной или анизотропной проводимости в объемном проводнике или когда геометрия электродной решетки сложна. После того, как значения внеклеточного потенциала были решены, модель нейронного кабеля может быть численно решена в вычислительном программном обеспечении нейронов. Объединение двух программ позволяет вычислять сложную нейронную клетку или сеть в неоднородном электрическом поле.
Простая двухэтапная модель ганглиозной клетки сетчатки при супрахороидальной стимуляции будет построена с использованием вышеупомянутых программ. В этом исследовании ганглиозная клетка сетчатки будет подвергаться воздействию диапазона величин импульсов электрического тока. Расположение клетки относительно стимула также варьируется, чтобы показать зависимость расстояние-порог. Кроме того, исследование включает в себя валидацию вычислительного результата по сравнению с исследованием in vivo порога активации коры с использованием различных размеров стимулирующего электрода12, а также исследование in vitro , показывающее взаимосвязь между расстоянием электрод-нейрон и порог активации13.
протокол
1. Настройка конечно-элементной модели для расчета электрического потенциала
- Определение этапов моделирования и сложности модели
ПРИМЕЧАНИЕ: Целью первого шага является уточнение цели моделирования, которое определит необходимые элементы модели и процедуру имитационного моделирования. Важным моментом, который следует учитывать, является поведение нервных клеток, которое должно быть показано моделью, и какой протокол тестирования потребуется для демонстрации этого поведения. Это исследование показывает зависимость расстояние-порог для нейрона, который стимулируется внеклеточным образом, а также кривую размера электрода-порога. Для этого необходима модель нейронных клеток, разделенная на различные участки (для включения вариаций морфологических и биофизических параметров в нейроне), чувствительная к внеклеточному напряжению, и моделирование диапазона размеров и положений электродов.- Определите исследовательский вопрос и экспериментальные переменные.
- Определите исследовательский вопрос и протокол тестирования, чтобы направлять построение модели. Лучше всего начать с четкого вопроса и построить модель максимально просто, чтобы ответить на него.
- Определение необходимых элементов для включения в полную модель
ПРИМЕЧАНИЕ: В этом подходе к моделированию клетка рассматривается как погруженная в электропроводящую среду, то есть биологическую ткань. Электрическая стимуляция происходит через этот «объемный проводник», то есть среду, что приводит к распределению электрического потенциала.- Основываясь на исследовательских вопросах и переменных для решения, решите, требуются ли оба элемента (FEM и модель нейронного кабеля). Если, например, моделирование требует одного электрода, который может быть упрощен в качестве точечного источника и что среда однородна, МКЭ может не понадобиться, и для его замены может потребоваться аналитический расчет внеклеточного электрического поля.
- Определите исследовательский вопрос и экспериментальные переменные.
- Загрузка и установка программного обеспечения
ПРИМЕЧАНИЕ: В исследовании использовались версии программных приложений (COMSOL, NEURON и Python Anaconda) и аппаратного обеспечения, указанного в Таблице материалов. Могут быть незначительные различия в шагах или результатах, если используются разные версии программного обеспечения или оборудования.- Загрузите программное обеспечение, соответствующее операционной системе компьютера, и при необходимости приобретите лицензию. Убедитесь, что загружены все необходимые модули моделирования, и установите все программное обеспечение.
- Сбор данных об анатомии ткани и клетки для моделирования
ПРИМЕЧАНИЕ: Для этого метода анатомические и биофизические параметры были взяты из эмпирических результатов. Вычислительные модели обычно смешивают параметры, измеренные у разных видов из-за недоступности данных. Для моделирования супрахориоидальной стимуляции в модель необходимо включить тканевые слои между стимулирующим и опорным электродами.- Соберите анатомию ткани из гистологических исследований.
- В эту модель включают сосудистую оболочку, ткань сетчатки и стекловидное тело, где каждый домен моделируется как прямоугольная призма для легкого построения модели. Соберите среднюю толщину ткани сетчатки из опубликованных гистологических данных14 , чтобы позже использовать ее в качестве высоты каждой призмы.
- Соберите данные морфологии одной клетки из окрашивания клеток или общедоступной базы данных нейронов.
- Загрузите подробную морфологию нейронов из базы данных, такой как NeuroMorpho.org, которая предоставляет функцию метаданных поиска для поиска соответствующего нейрона на основе вида, области мозга, типа клетки и т. Д. Для этого исследования найдите модель Го OFF RGC (D23WM13_27_1-OffRGC_msa)15 , введя Rabbit > New Zealand White в поле Species и Retina в поле Brain Region . Нажмите на модель и загрузите файл .swc.
- Соберите анатомию ткани из гистологических исследований.
- Сбор биофизических данных смоделированной клетки
ПРИМЕЧАНИЕ: Биофизические параметры включают значения электропроводности для каждого слоя ткани и электрические параметры нервной мембраны и ионных каналов.- Из-за доступности данных использовали значения электропроводности, которые были взяты у кролика16 для тканевой модели, в то время как динамика ионных каналов была основана на модели Шисби и Фольмейстера сетчатки17 тигровой саламандры.
- Построение геометрии конечно-элементной модели ткани и электрода в программном обеспечении FEM
ПРИМЕЧАНИЕ: Геометрия ткани и электродной решетки влияют на распределение электрического потенциала, что, в свою очередь, влияет на поведение нервных клеток. Следовательно, важно построить реалистичную геометрию среды, в которой находятся ячейки, а также электрода. Программное обеспечение FEM, используемое в этом учебнике, имеет графический интерфейс, который позволяет легко строить геометрию модели.- Настройка модели FEM в графическом интерфейсе программного обеспечения:
- Запустите программное обеспечение FEM и нажмите Мастер моделей > 3D. В списке Выбор физики разверните > Электрические поля и ток > электрические токи (ec) и нажмите кнопку Добавить. Нажмите « Исследование» и добавьте «Стационарное исследование» под опцией «Общие исследования », а затем нажмите «Готово» (дополнительный рисунок 1).
- Настройка единицы измерения и геометрических параметров электрода.
- В дереве конструктора моделей щелкните Параметры 1. В таблице введите 'elec_rad' в поле Имя и '50' в поле Выражение, чтобы создать электрод радиусом 50 единиц. Затем нажмите « Геометрия» и измените единицу длины на мкм, так как сома типичной ганглиевой клетки сетчатки составляет около 10 мкм в диаметре (дополнительный рисунок 2).
- Создание тканевых слоев с помощью блочных доменов
ПРИМЕЧАНИЕ: Для построения геометрии модели были использованы три блока для представления различных структур в глазу. Блок 1 представлял собой сосудистую оболочку, блок 2 - ткань сетчатки, а блок 3 - стекловидное тело.- Щелкните правой кнопкой мыши geometry 1 > Block , чтобы создать домен блока. Повторите этот шаг еще два раза, чтобы создать в общей сложности три блока. Для всех блоков установите для параметров Глубина и Ширина значение 5 000 мкм и измените параметр База (в разделе Положение) на Центр. Присвойте каждому блоку следующие значения высоты (в разделе Размер и форма) и z (в разделе Положение):
Блок 1: Высота = 112 мкм, z = 0 мкм
Блок 2: Высота = 151 мкм, z = 131,5 мкм
Блок 3: Высота = 5 000 мкм, z = 2 707 мкм
- Щелкните правой кнопкой мыши geometry 1 > Block , чтобы создать домен блока. Повторите этот шаг еще два раза, чтобы создать в общей сложности три блока. Для всех блоков установите для параметров Глубина и Ширина значение 5 000 мкм и измените параметр База (в разделе Положение) на Центр. Присвойте каждому блоку следующие значения высоты (в разделе Размер и форма) и z (в разделе Положение):
- Создание рабочей платы для добавления электрода в модель
- Щелкните правой кнопкой мыши геометрию 1 в дереве моделей и выберите Рабочая плоскость. Нажмите на Рабочую плоскость 1 и измените тип плоскости на Параллельную, нажмите кнопку Активировать выбор под типом плоскости и выберите нижнюю поверхность блока 1 (blk 1 > 1).
- Рисование дискового электрода на рабочей плоскости
- Нажмите « Геометрия плоскости » в разделе «Рабочая плоскость 1 » и нажмите « Эскиз» на главной панели инструментов. Выберите «Круг», щелкните в любом месте внутри прямоугольника на вкладке «Графика» и перетащите указатель, чтобы создать электрод диска. Измените радиус на 'elec_rad' μm, xw и yw на 0 мкм, а затем нажмите Build All.
- Назначение свойств материала каждому домену
ПРИМЕЧАНИЕ: Следуя шагам по построению геометрии, модель будет разделена на несколько «областей», которые представляют собой отдельные 3D-части, составляющие полную геометрию. Каждому домену должно быть присвоено значение электропроводности для расчета распределения электрического поля по всей модели.- В дереве моделей щелкните правой кнопкой мыши Материал > Пустой материал, а затем выберите Материал 1 и измените выбор на Ручной.
- Нажмите на домены в окне Графика, чтобы выбрать только домен 1. Выберите Свойства материала > Основные свойства > Электропроводность, нажмите кнопку Добавить в материал и измените значение Электропроводности на значение 0,043 С/м15.
- Повторите шаги для доменов 2 и 3 со значениями электропроводности 0,716 и 1,5516 См/м соответственно (дополнительный рисунок 3).
- Объединение 3D-модели: Чтобы связать модель, перейдите в дерево моделей и щелкните правой кнопкой мыши Mesh 1 > Free Tetrahedral. Нажмите на Free Tetrahedral 1 и выберите Build All.
ПРИМЕЧАНИЕ: Процесс сетки разбивает всю геометрию на более мелкие «элементы» (элемент — это виртуальный сегмент геометрии модели, где физические уравнения решаются численно). Сетка с меньшими элементами теоретически повышает точность аппроксимации, но является вычислительно исчерпывающей. Обычной практикой является запуск модели с разреженной сетки и запись результата моделирования, а затем непрерывное повторение моделирования с меньшими элементами сетки каждый раз и сравнение результатов. Процесс уточнения может остановиться, если нет существенной разницы в результатах расчета от последующих этапов уточнения.- Оценка качества сетки: щелкните правой кнопкой мыши на Сетке 1 и выберите Статистика, чтобы показать гистограмму качества элемента. Выполните описанные ниже действия по уточнению сетки, чтобы улучшить качество элементов.
ПРИМЕЧАНИЕ: Использование сетки по умолчанию может привести к образованию многих элементов низкого качества, что, в свою очередь, приводит к неточным вычислениям. В большинстве случаев требуется некоторая степень уточнения сетки. - Рафинирование сетки по периметру электрода
ПРИМЕЧАНИЕ: Области, где могут быть резкие изменения в электрическом поле, обычно требуют более утонченной сетки. Здесь была добавлена более плотная сетка по периметру электрода с помощью функции распределения краев.- Во-первых, удалите существующую свободную тетраэдрическую сетку 1. Затем щелкните правой кнопкой мыши на Mesh 1 > Distribution, щелкните Distribution 1, измените Геометрический уровень сущности на Edge и выберите Edges 19-22 (периметр дискового электрода).
- Установите для параметра Тип распределения значение Фиксированное количество элементов и измените в поле Количество элементов значение elec_rad*3/10 , чтобы сделать элементы достаточно маленькими.
- Уточнение сетки через сосудистую оболочку и ткань сетчатки
- В дереве моделей щелкните правой кнопкой мыши сетку 1 > Swept. Нажмите на Swept 1. Выберите Домены 1 и 2. Затем щелкните правой кнопкой мыши mesh 1 > Free Tetrahedral, установите для геометрической сущности значение Остаться и нажмите Build All. (Необязательно: еще раз проверьте гистограмму качества элементов, чтобы убедиться, что низкокачественные элементы были уменьшены пропорционально).
- Оценка качества сетки: щелкните правой кнопкой мыши на Сетке 1 и выберите Статистика, чтобы показать гистограмму качества элемента. Выполните описанные ниже действия по уточнению сетки, чтобы улучшить качество элементов.
- Настройка модели FEM в графическом интерфейсе программного обеспечения:
- Применение физики к конечно-элементной модели
ПРИМЕЧАНИЕ: «Физика» в программном обеспечении FEM представляет собой наборы математических уравнений и граничных условий, которые должны быть назначены модели. Это вычисление решения одновременного набора уравнений, которое осуществляется в ходе выполнения модели. Выбор физики для применения к геометрии зависит от физического явления, которое моделируется. Например, физика электрического тока, используемая в этой модели, наблюдает распределение электрического поля и пренебрегает магнитным (индуктивным) явлением. Другая физика может быть применена к геометрии, если будут решены другие физические проблемы (например, распределение температуры, механическое напряжение и т. Д.).- Выбор физики и применение граничных условий
ПРИМЕЧАНИЕ: Если необходимо применить импульс постоянного напряжения, граничное условие плавающего потенциала должно быть заменено граничным условием электрического потенциала.- Разверните узел Электрические токи 1 в дереве моделей и проверьте, указаны ли в списке Сохранение тока 1, Электрическая изоляция 1 и Начальные значения 1 . Затем щелкните правой кнопкой мыши на электрических токах 1 > земле (это присваивает 0 В отдаленной плоскости, имитируя отдаленный электрод сравнения) и нанесите его на поверхность, наиболее удаленную от электрода (поверхность 10).
- Затем щелкните правой кнопкой мыши электрические токи 1 > плавающий потенциал (это имитирует источник тока с постоянным током), назначенный дисковому электроду (поверхность 14), и измените значение I 0 на 1 [мкА], чтобы применить унитарный ток.
- Запуск моделирования с параметрической разверткой.
ПРИМЕЧАНИЕ: На этом шаге будет запущено моделирование, и была добавлена параметрическая подметание, где было выполнено несколько симуляций со значением параметра, измененным в каждом моделировании. Здесь параметр радиуса электрода был смещен, а распределение электрического потенциала для каждого моделирования сохранялось в файле модели. После выполнения моделирования ветвь Результаты в дереве моделей была заполнена мультисрезовым графом электрического потенциала (ec).- В дереве моделей щелкните правой кнопкой мыши исследование 1 > параметрической развертки. Щелкните Параметрическая очистка и в таблице настроек исследования нажмите кнопку Добавить, а затем выберите elec_rad для имени параметра.
- Введите '50, 150, 350, 500' для списка значений параметров и 'μm' для единицы параметра и нажмите «Вычислить», чтобы запустить исследование (дополнительный рисунок 4).
- Выбор физики и применение граничных условий

Рисунок 1: Создание геометрии tisssue. Геометрия блока была вставлена в модель FEM для представления ткани. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этого рисунка.
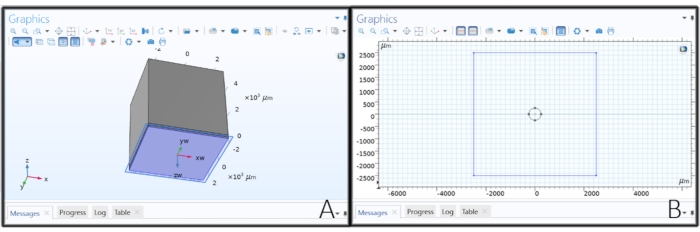
Рисунок 2: Создание геометрии электрода. (А) Создание рабочей плоскости для рисования дискового электрода. (B) Набросок круга на рабочей плоскости для создания дискового электрода. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этого рисунка.

Рисунок 3: Гистограмма качества элементов модели МКЭ. Гистограмма показала качество элементов по всей модели. Доработка сетки необходима, если значительная часть элементов находится в области низкого качества. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этого рисунка.
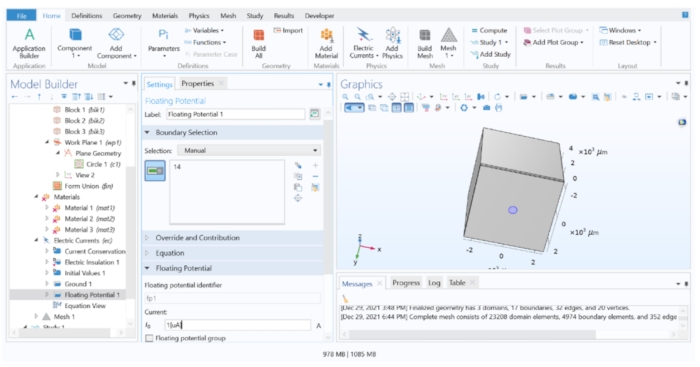
Рисунок 4: Присвоение электроду значения тока. Унитарный ток, приложенный к геометрии электрода в программном обеспечении FEM. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этого рисунка.
2. Импорт геометрии нейронной клетки в графический интерфейс вычислительного набора нейронов
- Построение геометрии модели ячейки
- Импорт морфологии с помощью функции Cell Builder.
- Запустите 'nrngui' из папки установки набора нейронов, щелкните Инструменты > Разное > Импорт 3D, а затем установите флажок Выбрать файл .
- Найдите загруженный файл .swc и нажмите кнопку Прочитать. После того, как геометрия была импортирована, нажмите «Экспортировать > cell Builder (дополнительный рисунок 5).
- Создание HOC-файла импортированной морфологии ячейки
- Перейдите на вкладку Подмножества и наблюдайте за подмножествами, которые были предопределены в модели (например, сома, аксон, базальный и т. Д.). Установите флажок Непрерывное создание , перейдите в раздел Управление > Экспорт и экспортируйте морфологию как 'rgc.hoc'.
- Просмотр морфологии клетки
- Нажмите tool > Model View > 1 Real Cells > Root Soma[0] на панели инструментов, щелкните правой кнопкой мыши на появившемся окне и выберите Axis Type > View Axis. При визуальном осмотре диаметр дендритного поля этой модели составляет около 250 мкм. Закройте окна NEURON на данный момент.
- Импорт морфологии с помощью функции Cell Builder.

Рисунок 5: Экспорт информации о модели нейронов в виде файла .hoc. Геометрия нейрона была экспортирована в файл .hoc для дальнейших модификаций. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этого рисунка.
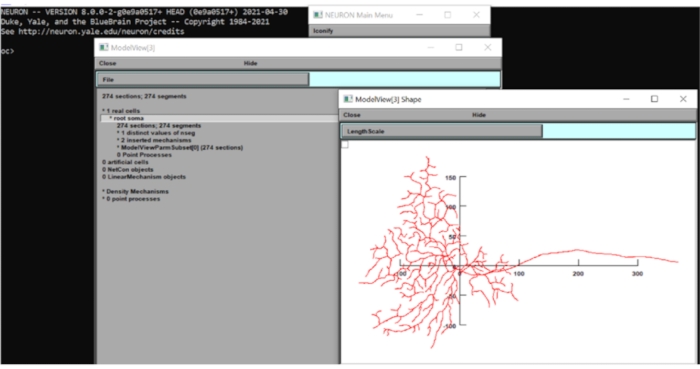
Рисунок 6: Измерение размерности нейрона. Морфология нейрона (вид сверху) отображалась в графическом интерфейсе вычислительного набора нейронов с наложенными осями x-y. Шкала была в мкм. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этого рисунка.
3. Программирование моделирования вычислений NEURON
- Настройка морфологии ячейки путем программирования на языке .hoc
ПРИМЕЧАНИЕ: Морфология ячейки может быть скорректирована с помощью функции Cell Builder графического интерфейса. Однако показано, как это можно сделать, отредактировав файл .hoc для ускорения процесса. Файл .hoc определяет топологию (физические связи между каждой частью нейронов), морфологию (длину, диаметр и расположение каждого участка нейрона) и биофизические свойства (параметры ионного канала) моделируемой клетки. Полную документацию по программированию .hoc можно найти по адресу: https://neuron.yale.edu/neuron/static/new_doc/index.html#,- Откройте полученный файл .hoc с помощью текстового редактора (например, Блокнота). Добавьте начальный сегмент аксона длиной 40 мкм и узкий аксональный сегмент длиной 90 мкм, близкий к соме, как описано в Sheasby and Fohlmeister17, а также измените длину дендритов таким образом, чтобы размер дендритного поля стал 180 мкм, чтобы соответствовать ячейке G1 в Rockhill, et al.18.
- Создание новых секций ячеек и определение топологических связей для каждого раздела.
- Чтобы создать новые секции ячеек для начального сегмента аксона (AIS) и узкого аксонального сегмента (NS), добавьте следующие строки в начало файла rgc.hoc:
создать АИС, НС // Объявление сотовых отсеков под названием АИС и НС
Затем замените строку 'соединить аксон(0), сома[1](1)' на:
соединить ais(0), soma[1](1) // Подключение первого сегмента АИС к концу soma[1]
connect ns(0), ais(1) // Подключение первого сегмента NS к концу АИС
подключить аксон(0), ns(1) // Подключение первого сегмента аксона к концу NS
- Чтобы создать новые секции ячеек для начального сегмента аксона (AIS) и узкого аксонального сегмента (NS), добавьте следующие строки в начало файла rgc.hoc:
- Определение 3D-положений, диаметров и длины секций ячеек
- Определите 3D-положения и диаметры отсеков AIS и NS, написав эти строки в скобках 'proc shape3d_31()':
ais { pt3dadd(-2.25, -1.55, 0, 1) // Первые три числа являются координатой xyz, а диаметр равен 1 мкм
pt3dadd(37.75, -1.55, 0, 1)} // Первая точка при x = -2.25 мкм, а последняя точка при x = 37.75 мкм
ns { pt3dadd(37.75, -1.55, 0, 0.3) // 3D координаты и диаметр для сегментов NS
pt3dadd(127.75; -1.55, 0, 0.3)} - В конце файла сместите 3D-координату аксона так, чтобы его начальная точка соответствовала конечной точке NS, введя:
axon {for i=0,n3d()-1 {pt3dchange(i, x3d(i)+130, y3d(i),z3d(i)-5, diam3d(i))}} //Shift координату x - В конце файла сократите дендритные отсеки на 18%, набрав:
forsec basal {L=L*0.82} // Масштабирование длины для уменьшения размера дендритного поля
define_shape() // Заполнение недостающей 3D-информации
- Определите 3D-положения и диаметры отсеков AIS и NS, написав эти строки в скобках 'proc shape3d_31()':
- Создание новых секций ячеек и определение топологических связей для каждого раздела.
- Откройте полученный файл .hoc с помощью текстового редактора (например, Блокнота). Добавьте начальный сегмент аксона длиной 40 мкм и узкий аксональный сегмент длиной 90 мкм, близкий к соме, как описано в Sheasby and Fohlmeister17, а также измените длину дендритов таким образом, чтобы размер дендритного поля стал 180 мкм, чтобы соответствовать ячейке G1 в Rockhill, et al.18.
- Определение количества сегментов для каждого раздела
ПРИМЕЧАНИЕ: Каждый участок нейрона может быть пространственно дискретизирован, подобно процессу сетки в модели FEM. Пространственная дискретизация делит нейрон практически на более мелкие сегменты, где должны быть выполнены вычисления. Для числа сегментов 'nseg' убедитесь, что нечетные числа используются для обеспечения наличия внутреннего узла в средней точке секции ячейки, и попробуйте утроить число nseg до тех пор, пока вычисление не даст последовательный результат9. Большее количество сегментов даст более точное численное приближение, но также увеличит вычислительную нагрузку.- Чтобы проиллюстрировать процесс дискретизации, добавьте следующие строки в файл rgc.hoc, чтобы разделить нейронные секции в соматическом и аксональном подмножествах на несколько сегментов:
forsec somatic {nseg=31}
forsec axonal {nseg=301}
Другие разделы модели также необходимо дискретизировать, набрав эти строки, но изменив имя подмножества (после «forsec») и количество сегментов (после «nseg») по желанию.
- Чтобы проиллюстрировать процесс дискретизации, добавьте следующие строки в файл rgc.hoc, чтобы разделить нейронные секции в соматическом и аксональном подмножествах на несколько сегментов:
- Вставка настраиваемых механизмов ионных каналов
- Запись настраиваемых механизмов ионных каналов в виде файлов .mod: Чтобы применить механизмы ионных каналов, создайте файлы .mod и вставьте файлы в часть биофизического раздела файла .hoc, выполнив шаги 3.3.1-3.3.3. Файл .mod содержит переменные и дифференциальные уравнения, которые необходимо решить для каждого ионного канала.
ПРИМЕЧАНИЕ: Правильные определения и реализации механизма ионных каналов имеют решающее значение для точного моделирования нейронов. При записи файлов .mod проверьте, являются ли единицы измерения правильными (предоставляемая утилита 'modlunit', которую можно запустить для проверки согласованности единиц) и что уравнения написаны правильно. Чтобы проверить, что механизмы ионных каналов верны, ток для каждого ионного канала во время внутриклеточной или внеклеточной стимуляции может быть построен и сопоставлен с эмпирическими результатами.- Ионные каналы с напряжением
ПРИМЕЧАНИЕ: Файл .mod для создания ионного канала с напряжением обычно включает блок DERIVATIVE , который имеет дифференциальное уравнение для решения, блок BREAKPOINT , который имеет команды для решения дифференциальных уравнений с использованием выбранного метода численного приближения, и блоки PROCEDURE , которые сообщают программе вычислить параметры gating (например, mt, ht и d в этом примере). Этот код будет вычислять значения ионного тока, проходящего через канал для каждого временного шага.- Чтобы проиллюстрировать процесс, создайте зависимый от напряжения канал Ca, который имеет дифференциальные уравнения первого порядка для решения переменных gating.
- Откройте новый файл в текстовом редакторе и введите строки в поле Дополнительный материал, определяющий зависящий от напряжения канал Cat. Сохраните этот файл как Cat.mod в той же папке, что и файл .hoc. Этот процесс необходимо повторить для других ионных каналов, которые содержит модельный нейрон.
- Зависимые от напряжения и концентрации ионные каналы
- Кинетика некоторых ионных каналов, таких как кальциево-активированные калиевые каналы в ганглиозных клетках сетчатки, зависит от внутриклеточной концентрации кальция, помимо трансмембранного напряжения19. Чтобы смоделировать этот тип механизма, создайте файл с именем KCa.mod и введите линии, как показано в разделе Дополнительные ионные каналы, зависящие от материала и концентрации. В этом файле .mod была рассчитана переменная 'cai', которая определяется как внутренняя концентрация иона Ca, а затем эта переменная используется в уравнении для вычисления тока iKCa.
- Ионные каналы с напряжением
- Компиляция файлов .mod
- Скомпилируйте все файлы .mod, запустив утилиту mknrndll вычислительного пакета нейронов из папки установки. Найдите папку, в которой содержатся MOD-файлы, и нажмите кнопку Compile, чтобы создать файлы O и C. После этого механизмы могут быть вставлены в эту модель ячейки.
- Применение файлов .mod в основном файле модели NEURON.
ПРИМЕЧАНИЕ: Помимо вставки ионных каналов, максимальная проводимость Na была определена только для «соматического» подмножества. При необходимости мы могли бы индивидуально настроить максимальную проводимость мембраны для различных сегментов нейронов.- Для краткости объедините все механизмы ионных каналов в один файл .mod (Файл Supplementary Material-Complete .mod). Вставьте комбинированный файл .mod, содержащий все ионные каналы и пассивный канал утечки, во все сегменты в «соматическом» подмножестве, введя строки ниже в процедуре «biophys» файла rgc.hoc:
forsec somatic {insert rgcSpike
вставить pas // пассивный канал утечки
gnabar_rgcSpike = 80e-3
g_pas = 0,008e-3 // проводимость мембраны утечки}
- Для краткости объедините все механизмы ионных каналов в один файл .mod (Файл Supplementary Material-Complete .mod). Вставьте комбинированный файл .mod, содержащий все ионные каналы и пассивный канал утечки, во все сегменты в «соматическом» подмножестве, введя строки ниже в процедуре «biophys» файла rgc.hoc:
- Установка удельного сопротивления аксоплазмы
- Клетки имеют аксоплазматическое удельное сопротивление, которое может быть изменено на каждый отсек. Для этой модели все сегменты имеют одинаковое удельное сопротивление 110 Ω·см. Измените удельное сопротивление аксоплазмы в файле rgc.hoc:
forall {Ra = 110}
- Клетки имеют аксоплазматическое удельное сопротивление, которое может быть изменено на каждый отсек. Для этой модели все сегменты имеют одинаковое удельное сопротивление 110 Ω·см. Измените удельное сопротивление аксоплазмы в файле rgc.hoc:
- Запись настраиваемых механизмов ионных каналов в виде файлов .mod: Чтобы применить механизмы ионных каналов, создайте файлы .mod и вставьте файлы в часть биофизического раздела файла .hoc, выполнив шаги 3.3.1-3.3.3. Файл .mod содержит переменные и дифференциальные уравнения, которые необходимо решить для каждого ионного канала.
- Вставка внеклеточных механизмов и определение формы импульсного сигнала
- Вставка внеклеточного механизма в клеточную модель
- Чтобы клеточная модель реагировала на внеклеточное напряжение, вставьте внеклеточный механизм во все сегменты, набрав строку в нижней части файла rgc.hoc:
forall {вставить внеклеточный}
- Чтобы клеточная модель реагировала на внеклеточное напряжение, вставьте внеклеточный механизм во все сегменты, набрав строку в нижней части файла rgc.hoc:
- Создание двухфазного импульса
ПРИМЕЧАНИЕ: В этой демонстрации создается двухфазный импульс постоянного тока, который настраивается пользователем по ширине импульса, межфазному зазору и количеству повторений путем создания процедуры в файле .hoc. Для более структурированной программы используйте файл rgc.hoc в качестве файла для создания модели ячейки, в то время как процесс стимуляции применяется в отдельном файле .hoc, который загружает модель ячейки, к которой применяется стимуляция.- Создайте новый текстовый файл с именем stimulation.hoc и запустите код, загрузив файл модели ячейки; затем сделайте двухфазный импульс, определив процедуру, как показано в разделе Дополнительный материал - Создание двухфазного импульса в моделировании нейронов.
ПРИМЕЧАНИЕ: На этом этапе создается катодный двухфазный импульс постоянного тока, где параметры стимула должны быть объявлены пользователем при выполнении моделирования. В настоящее время величина анодного и катодного импульсов составляет ±1 мкА, но эта величина должна изменяться в зависимости от тока стимуляции, подаваемого дисковым электродом.
- Создайте новый текстовый файл с именем stimulation.hoc и запустите код, загрузив файл модели ячейки; затем сделайте двухфазный импульс, определив процедуру, как показано в разделе Дополнительный материал - Создание двухфазного импульса в моделировании нейронов.
- Вставка внеклеточного механизма в клеточную модель
4. Запуск и автоматизация нескольких симуляций
- Комбинирование моделей
- Извлечение координат для узлов в модели нейронной клетки
ПРИМЕЧАНИЕ: Целью объединения симуляций является получение значений внеклеточного потенциала, соответствующих каждому узлу клеточной модели. Однако координаты двух моделей должны быть выровнены. В этом примере центральный сегмент сомы (soma(0,5)) выровняли так, чтобы он лежал на горизонтальной средней плоскости ткани сетчатки (соответствующей слою ганглиозных клеток сетчатки), причем центральный узел сомы располагался прямо над центром дискового электрода.- Откройте модель FEM и запишите координату контрольной точки (например, горизонтальной промежуточной плоскости ткани сетчатки, над центром дискового электрода), и в этом случае она составляет [0, 0, 131,5] мкм.
- В вычислительном наборе нейронов создайте файл с именем calculateCoord.hoc, чтобы извлечь координаты центроида каждого сегмента и сместить каждую секцию так, чтобы центральный сегмент сомы имел ту же координату, что и контрольная точка в модели FEM (Дополнительный материал - Вычисление координаты каждого узла).
- Сохранение координатных точек в текстовый файл
- Запустите файл calculateCoord.hoc (дважды щелкнув в проводнике или открыв графический интерфейс вычислительного набора нейронов; затем щелкните Файл > загрузить hoc на панели инструментов). Сохраните координаты для внеклеточных значений напряжения, которые будут оцениваться, в текстовый файл с именем «координаты.dat».
- Запуск моделирования и сохранение данных о напряжении в текстовый файл
ПРИМЕЧАНИЕ: На этом этапе мы извлекли рассчитанные внеклеточные значения из модели FEM, но мы сохранили данные только из соответствующих координат, которые совпадают с центром каждого сегмента клетки. Следуйте шагу 4.1.6.2, когда для экспорта требуется большое количество потенциалов.- Откройте файл модели ткани в программном обеспечении FEM; перейдите к заголовку Результаты в дереве моделей и нажмите «Экспортировать > данные > данных 1». Убедитесь, что для набора данных установлено значение Study 1/Parametric Solutions 1, а затем введите 'V' в столбце Выражение и 'mV' в столбце Unit .
- В разделе Выходные данные измените имя файла на extracellular.dat и выберите Точки для оценки в: Из файла. Загрузите координаты.dat для поля Файл координат , а затем нажмите кнопку Экспорт.
- Применение двухфазного импульса к модели ячейки
ПРИМЕЧАНИЕ: На этом этапе доступны значения внеклеточного напряжения для каждого сегмента ячейки в одну точку времени (где ток составляет 1 мкА). Поскольку исследование направлено на то, чтобы подвергнуть клетку двухфазному импульсу, заставить внеклеточное значение напряжения, испытываемое клеткой, изменяться со временем, используя метод «vector.play».- Добавьте линии, показанные в Дополнительном материале- Применение двухфазного импульса при стимуляции.hoc.
- Запуск комбинированного моделирования
ПРИМЕЧАНИЕ: Для выполнения моделирования необходимо определить временной интервал 'dt' для числовых приближений. Подобно nseg, более короткий dt может увеличить вычислительную точность, но также увеличивает вычислительную стоимость.- Добавьте строки, показанные в Дополнительном материале-Выполнение моделирования нейрона, в конец stimulation.hoc. Затем дважды щелкните файл stimulation.hoc, чтобы загрузить сценарий и автоматически запустить симуляцию. Трансмембранный потенциал интересующего сегмента может быть отображен в графическом интерфейсе вычислительного набора нейронов (шаг 4.2.1) или сохранен в текстовый файл для чтения в других программах (шаг 4.1.6.1.2). Выполните шаги 4.1.6.1 и 4.1.6.2, если необходимо экспортировать повторные расчеты и большое количество мембранных потенциалов.
- Дополнительно: Автоматизация моделирования
ПРИМЕЧАНИЕ: Чтобы найти пороговую амплитуду, цикл моделирования несколько раз с другой амплитудой тока каждый раз. Другая автоматизация может потребоваться для поиска порога для нейронов, расположенных в разных положениях относительно стимулирующего электрода. Шаг автоматизации может быть выполнен в вычислительном наборе нейронов с использованием процедуры, а также в программном обеспечении FEM с использованием скрипта, называемого «методом».- Автоматизация моделирования нейронов для нахождения пороговой амплитуды
ПРИМЕЧАНИЕ: Пакет моделирования нейронов может быть выполнен автоматически. Следующие шаги реализованы в программе моделирования нейронов для поиска пороговых амплитуд нейронов при различных параметрах стимуляции.- Создайте процедуру для повторного моделирования в программе моделирования нейронов: в stimulation.hoc создайте вектор, содержащий диапазон амплитуды тока для тестирования. Затем создайте процедуру для применения амплитуды тока и записи любого присутствия всплеска (положительное изменение от отрицательного к положительному трансмембранному напряжению), и пороговая амплитуда определяется как самая низкая амплитуда тока, которая вызывает всплеск. Для этого определите процедуру под названием findTh() (Дополнительная закольцовка материала в диапазоне амплитуд тока) в конце файла stimulation.hoc
- Сохранение ответа на пороговом значении текстового файла: добавьте следующие строки в процедуру findTh() в stimulation.hoc, чтобы сохранить рассчитанные значения напряжения трансмембраны для всех нейронных отсеков из каждого временного шага в текстовом файле:
sprint(saveFileName, "Response_%d.dat", th) // Сохранить пороговое значение
saveFile.wopen(saveFileName)
для i=0,(responseVector.size()-1){
saveFile.printf("%g,", responseVector.x[i])
if(i==responseVector.size()-1) {saveFile.printf("%g\n", responseVector.x[i])
saveFile.close(saveFileName)
}}
- Автоматизация в программном обеспечении FEM для поиска значений напряжения для нейронов в разных местах
ПРИМЕЧАНИЕ: Еще одна автоматизация, которая может быть сделана, - это автоматическое получение внеклеточных значений напряжения для нейронов в разных местах. Меню Application Builder в программном обеспечении FEM предоставляет средства для определения «метода» или скрипта для автоматизации шагов, необходимых программному обеспечению для выполнения вычислений. Для демонстрации расположение ячейки в x-направлении смещается в 5 раз на шаге 100 мкм (дополнительный рисунок 6).- Написание кода для автоматизации МКЭ-симуляций.
- Перейдите в Построитель приложений, щелкните правой кнопкой мыши Методы в дереве Конструктор приложений, выберите Новый метод и нажмите кнопку ОК. Перейдите в настройки > файлов > методы, установите флажок Просмотреть все коды и нажмите кнопку «ОК».
- Напишите сценарий .hoc, который загрузит файл координат, сместит значения в соответствии с нужным местоположением и сохранит текстовый файл, содержащий значения напряжения для нового местоположения ячейки, введя коды, показанные в методе дополнительного определения материала для автоматизации моделирования FEM.
- Выполнение автоматических шагов в программном обеспечении FEM: переключение на построитель моделей, метод разработки > запуска > метод 1. Это приведет к созданию .dat файлов с соответствующими значениями напряжения, называемыми extracellular_1.dat, extracellular_2.dat и т. Д.
- Написание кода для автоматизации МКЭ-симуляций.
- Зацикливание симуляций на языке программирования общего назначения
ПРИМЕЧАНИЕ: Чтобы зациклить моделирование, соответствующий текстовый файл должен быть загружен в моделирование нейронного вычислительного пакета каждый раз, и язык программирования20 , который может легко загружать и манипулировать текстовыми файлами, удобен для выполнения этого шага. Для этого шага можно использовать любую удобную интегрированную среду разработки (IDE)21 .- Откройте выбранную среду IDE, щелкните Новый файл , чтобы создать новый сценарий. Здесь в этом примере используется файл .py. Введите строки, показанные в разделе Дополнительный материал-Выполнение моделирования на языке программирования общего назначения.
- Наконец, нажмите Run или нажмите F5 , чтобы запустить скрипт, который также откроет графический интерфейс (дополнительный рисунок 7).
- Автоматизация моделирования нейронов для нахождения пороговой амплитуды
- Извлечение координат для узлов в модели нейронной клетки
- Отображение данных моделирования
ПРИМЕЧАНИЕ: Следуя всем описанным выше шагам, результаты моделирования должны храниться в текстовых файлах, содержащих пороговое значение и трансмембранный потенциал на пороговом значении. Тем не менее, пользователь имеет возможность отображать результат моделирования во время моделирования с использованием графического интерфейса NEURON.- График ответа модели нейрона на внеклеточную стимуляцию в графическом интерфейсе вычислительного набора нейронов. Для этого запустите stimulation.hoc, нажмите на Graph > Voltage Axis на панели инструментов, а в окне графика щелкните правой кнопкой мыши в любом месте и выберите Plot What.
- Введите 'axon.v(1)' в поле Variable to Graph , что означает, что он будет отображать трансмембранный потенциал последнего сегмента аксона за шаг времени.
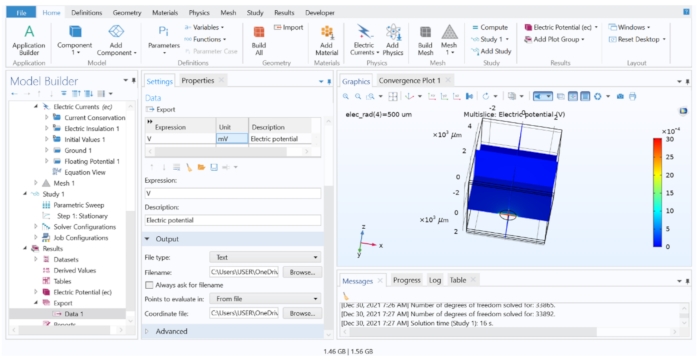
Рисунок 7: Отображение и экспорт результатов вычислений FEM в текстовый файл. Окно Графика, показывающее многосрезовый график электрического потенциала в V. Параметры параметра экспорта данных позволяли экспортировать вычисляемую переменную в текстовый файл. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этого рисунка.
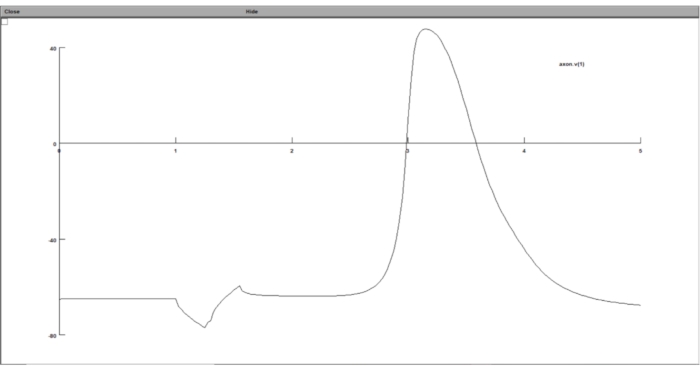
Рисунок 8: Отображение графика трансмембранного потенциала с помощью графика напряжения. Трансмембранный потенциал нейрона отображался в графическом интерфейсе вычислительного набора нейронов. Ось x — это время в мс, а ось y — трансмембранный потенциал выбранного сегмента нейрона в мВ. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этого рисунка.
Результаты
Мы провели два протокола моделирования, чтобы продемонстрировать использование модели. Первый протокол включал изменение размера электрода при сохранении местоположения нейрона и параметров электрического импульса одинаковыми. Второй протокол включал смещение нейрона в x-направлении с шагом 100 мкм, в то время как размер электрода оставался постоянным. Для обоих протоколов использовался импульс одного катодно-первого двухфазного импульса шириной 0,25 мс с межфазным промежутком 0,05 мс. Для первого протокола радиус электрода варьировался до 50, 150, 350 и 500 мкм, в то время как для второго протокола радиус электрода поддерживался на постоянном уровне 50 мкм.
Модель, описанная здесь, показала, что увеличение размера супрахориоидального электрода при ширине импульса 0,25 мс увеличивает порог активации модельного нейрона (рисунок 9A). Этот результат отражал результаты in vivo от Liang et al.12, которые показали, что порог активации коры увеличивается с увеличением размера электрода при этой ширине импульса.
Величины порогов активации модели отличаются от эмпирических результатов из-за нескольких факторов. Во-первых, эта модель включает только одну RGC определенного типа, которая может отсутствовать в группе клеток, активируемых в исследовании in vivo . Далее, эта модель не включала сеть сетчатки, которая может способствовать активации RGC через возбуждающие входы от биполярных клеток. Другой возможной причиной расхождения является расстояние электрод-сетчатка. Возможно, что расстояние электрод-сетчатка в исследовании in vivo было ниже, чем в этой модели из-за анатомической изменчивости или хирургического вмешательства. Следовательно, мы переоценили расстояние между электродом и сетчаткой и, следовательно, порог активации. Также важно отметить, что, хотя это не было продемонстрировано в наших результатах, моделирование порога одной клетки часто недооценивало корковый порог in vivo . Это связано с техническими ограничениями в корковых измерениях (в первую очередь связанными с отношением сигнал/шум), что кортикальная активность обычно обнаруживается только после активации нескольких ганглиозных клеток сетчатки. В результате следует ожидать расхождения в величине порогов активации сетчатки и коры. Несмотря на эти различия, данная модель успешно показала тенденцию к увеличению порога активации за счет увеличения размера электрода. Это произошло из-за отсутствия области высокого электрического поля по сравнению с окружающей средой при увеличении размера электрода, что не благоприятствовало нейронной активации22.
Затем мы наблюдали характеристики потенциала действия для проверки модели, описанной здесь. Латентность, или время между началом стимула и пиком всплеска потенциала действия, варьировалась от 1 до 2,2 мс (рисунок 9B). Это соответствовало всплеску короткой задержки из-за несетевой опосредованной активации сетчатки23. Ширина шипа этой модели составляла 1 мс, и это в том же диапазоне, что и ширина шипа RGC кролика, измеренная in vitro24.
Во втором протоколе стимуляции варьировалось только расположение нейрона по оси X (по длине аксона) относительно электрода. На расстоянии 0 центроид сечения сомы находился непосредственно над центром дискового электрода. Отрицательное расстояние означает, что дисковый электрод был расположен ближе к аксональной стороне, в то время как положительное расстояние означает, что дисковый электрод был расположен ближе к дендритной стороне. Модель показала, что самый низкий порог достигался, когда узкий сегмент аксона находился непосредственно над дисковым электродом, и он увеличивался по мере увеличения x-расстояния (рисунок 9C). Перемещение электрода дальше к дистальному аксону приводило к более низкому порогу по сравнению с перемещением электрода к дендритам из-за наличия начального сегмента аксона и узкого сегмента, где натриевые каналы более распространены. Этот результат согласуется с выводом in vitro от Jensen et al.13, где RGC кроликов стимулировали ультратонким микроэлектродом, а порог активации был самым высоким, когда электрод смещался ближе к дендритам.

Рисунок 9: Результаты метода моделирования. (А) Пороги активации для ганглиозной ячейки сетчатки, расположенной над дисковым электродом. Радиус электрода изменялся (50, 150, 350 и 500 мкм), а порог увеличивался с увеличением размера электрода. (B) Форма потенциала действия нейронной модели при ширине импульса 0,25 мс. Потенциалы действия на пороге для разных размеров электродов имеют одинаковую ширину шипа 1 мс, но задержка увеличивается с увеличением размера электрода. Время начала стимула составляло 1 мс, а катодная фаза вызывала деполяризацию на мембране, но не достаточную, чтобы вызвать потенциал действия. (C) Нейрон был смещен вдоль оси X, и пороги активации показали, что самый низкий порог был достигнут нейроном, чья сома была расположена прямо над центром электрода. Радиус электрода составлял 50 мкм. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этого рисунка.
Дополнительный рисунок 1: Инициализация модели конечных элементов. Типы Study и Physics определяют список уравнений, решаемых в модели. Они были установлены во время первоначального создания файла модели FEM, но также могут быть изменены / добавлены после создания модели. Пожалуйста, нажмите здесь, чтобы загрузить этот файл.
Дополнительный рисунок 2: Изменение единицы длины. Единица длины и угловая единица определяют единицы, используемые в процессе определения геометрии. Пожалуйста, нажмите здесь, чтобы загрузить этот файл.
Дополнительный рисунок 3: Вставка свойства материала. Свойства материала были определены для каждого домена в 3D-модели. Доступные свойства материала были перечислены в окне Свойства материала в окне Настройка материала. Для расчета электрического потенциала было определено только свойство электропроводности. Пожалуйста, нажмите здесь, чтобы загрузить этот файл.
Дополнительный рисунок 4: Создание параметрического исследования для циклического просмотра списка значений параметров. Параметрическое исследование позволило программному обеспечению FEM автоматически повторять вычисления и изменять значение радиуса электрода для каждого повтора. Результаты расчетов сохранялись для каждого повтора. Пожалуйста, нажмите здесь, чтобы загрузить этот файл.
Дополнительный рисунок 5: Импорт морфологии нейрона из файла SWC. Вычислительный набор нейронов был способен считывать SWC-файл, полученный от трассировки нейронов. Импортированный файл содержит информацию о морфологии и топологии каждого сегмента нейрона. Пожалуйста, нажмите здесь, чтобы загрузить этот файл.
Дополнительный рисунок 6: Автоматизация операций МКЭ путем определения метода. Метод был определен путем написания сценария для автоматизации процессов в программном обеспечении FEM, что не может быть сделано путем определения параметрического исследования. Пожалуйста, нажмите здесь, чтобы загрузить этот файл.
Дополнительный рисунок 7: Интеграция моделей и автоматизация моделирования с использованием языка программирования общего назначения. Язык программирования общего назначения использовался для зацикливания моделирования нейронов, одновременно изменяя внеклеточный файл напряжения, используемый в качестве входа, и файл напряжения нейронного отклика в качестве выхода для каждого шага в цикле. Пожалуйста, нажмите здесь, чтобы загрузить этот файл.
Дополнительный материал: Командные строки для (1) определения зависимого от напряжения канала Cat. (2) Зависимые от напряжения и концентрации ионные каналы. (3) Полный файл .mod. (4) Создание двухфазного импульса в моделировании нейронов. (5) Вычисление координат каждого узла. (6) Применение двухфазного импульса. (7) Выполнение моделирования нейронов. (8) Зацикливание в диапазоне амплитуд тока. (9) Определение метода автоматизации моделирования МКЭ. (10) Запуск симуляций на языке программирования общего назначения. Пожалуйста, нажмите здесь, чтобы загрузить этот файл.
Обсуждение
В этой статье мы продемонстрировали рабочий процесс моделирования, который сочетает в себе моделирование конечных элементов и биофизических нейронов. Модель очень гибкая, так как ее можно модифицировать по своей сложности в соответствии с различными целями, и она обеспечивает способ проверки результатов на основе эмпирических результатов. Мы также продемонстрировали, как мы параметризовали модель для обеспечения автоматизации.
Двухэтапный метод моделирования сочетает в себе преимущества использования МКЭ и вычислительного набора нейронов для решения уравнения кабеля нейрона в присутствии внеклеточной стимуляции. МКЭ полезен для точного вычисления внеклеточного поля по всему объемному проводнику, что часто нецелесообразно решать аналитически в случае сложной геометрии или неоднородности проводимости. Вычислительная стоимость этой модели также относительно низка, так как предполагается статическое условие.
Хотя описанный метод моделирования является преимуществом в своей простоте использования и гибкости, у этого рабочего процесса моделирования существуют ограничения. Во-первых, этот метод не допускал наличия нервной мембраны при расчете электрического поля. Joucla et al.25 сравнили двухэтапный метод со всем методом FEM, где нейронная геометрия и свойства мембраны были включены в модель FEM. Они показали, что включение нейрона в расчет электрического поля изменит расчет трансмембранного потенциала, когда в геометрию будет включена более крупная клеточная структура, такая как тело клетки. В частности, упрощение геометрии нейрона в двухступенчатом методе означает, что трансмембранный потенциал любой точки в компартменте представлен трансмембранным потенциалом в узле или центральной точке отсека. Напротив, модель всего МКЭ, предложенная Джуклой, включала явное представление 3D-геометрии нейрона, что позволяло индивидуально оценивать трансмембранный потенциал в любой точке внутри отсека. Таким образом, модель всей МКЭ может быть более подходящей, если требуется точная форма и местоположение трансмембранного потенциала. Однако этот метод вычислительно дороже, чем двухэтапный метод.
Второе ограничение метода моделирования касается доступности данных морфологии и кинетики ионов. Модель, используемая здесь, была основана на данных тигровой саламандры, которые были использованы для моделирования RGC других видов, но, возможно, были различия в типах присутствующих ионных каналов, которые не были выяснены. Следовательно, в некоторых случаях может потребоваться выполнение работ in vitro для корректировки параметров ионного канала.
В-третьих, стоимость программного обеспечения FEM может быть ограничением. В этом случае альтернативой может быть программа26 FEM с открытым исходным кодом, которая имеет встроенный решатель уравнений Пуассона. Помимо используемого программного обеспечения FEM, программное обеспечение, используемое в этом рабочем процессе, является бесплатным. В то время как используемое программное обеспечение FEM предлагает интуитивно понятный графический интерфейс и готовое к использованию моделирование электрического тока, можно выполнять вычисления внеклеточных значений в программном обеспечении общего назначения. Однако это потребовало бы ручного определения физических уравнений и численных методов для решения уравнений27. Кроме того, этот метод может быть утомительным, когда используется сложная геометрия ткани или электродного массива.
Раскрытие информации
Авторы заявляют об отсутствии конкурирующих интересов.
Благодарности
Это исследование финансируется Грантом проекта Национального совета по здравоохранению и медицинским исследованиям (номер гранта 1109056).
Материалы
| Name | Company | Catalog Number | Comments |
| Computer workstation | N/A | N/A | Windows 64-bit operating system, at least 4GB of RAM, at least 3 GB of disk space |
| Anaconda Python | Anaconda Inc. | Version 3.9 | The open source Individual Edition containing Python 3.9 and preinstalled packages to perform data manipulation, as well as Spyder Integrated Development Environment. It could be used to control the simulation, as well as to display and analyse the simulation data. |
| COMSOL Multiphysics | COMSOL | Version 5.6 | The simulation suite to perform finite element modelling. The licence for the AC/DC module should be purchased. The Application Builder capability should be included in the licence to follow the automation tutorial. |
| NEURON | NEURON | Version 8.0 | A freely-distributed software to perform the computation of neuronal cells and/or neural networks. |
Ссылки
- Greenberg, R. J., Velte, T. J., Humayun, M. S., Scarlatis, G. N., de Juan, E. A computational model of electrical stimulation of the retinal ganglion cell. IEEE Transactions on Bio-medical Engineering. 46 (5), 505-514 (1999).
- Guo, T., et al. Mediating retinal ganglion cell spike rates using high-frequency electrical stimulation. Frontiers in Neuroscience. 13, 413(2019).
- Loizos, K., et al. Increasing electrical stimulation efficacy in degenerated retina: Stimulus waveform design in a multiscale computational model. IEEE Transactions on Neural Systems and Rehabilitation Engineering. 26 (6), 1111-1120 (2018).
- Cao, X., Sui, X., Lyu, Q., Li, L., Chai, X. Effects of different three-dimensional electrodes on epiretinal electrical stimulation by modeling analysis. Journal of Neuroengineering and Rehabilitation. 12 (1), 73(2015).
- Wilke, R. G. H., Moghadam, G. K., Lovell, N. H., Suaning, G. J., Dokos, S. Electric crosstalk impairs spatial resolution of multi-electrode arrays in retinal implants. Journal of Neural Engineering. 8 (4), 046016(2011).
- AC/DC module user's guide. COMSOL AB. , Available from: https://doc.comsol.com/5.4/doc/com.comsol.help.acdc/ACDCModuleUsersGuide.pdf (2018).
- Malmivuo, P., Malmivuo, J., Plonsey, R. Bioelectromagnetism: Principles and Applications of Bioelectric and Biomagnetic Fields. , Oxford University Press. New York. (1995).
- Rall, W. Electrophysiology of a dendritic neuron model. Biophysical Journal. 2, 145-167 (1962).
- Carnevale, N. T., Hines, M. L. The Neuron Book. , Cambridge University Press. Cambridge. (2006).
- Rattay, F. The basic mechanism for the electrical stimulation of the nervous system. Neuroscience. 89 (2), 335-346 (1999).
- Hodgkin, A. L., Huxley, A. F. A quantitative description of membrane current and its application to conduction and excitation in nerve. The Journal of Physiology. 117 (4), 500-544 (1952).
- Liang, T., et al. Threshold suprachoroidal-transretinal stimulation current required by different-size electrodes in rabbit eyes. Ophthalmic Research. 45 (3), 113-121 (2011).
- Jensen, R. J., Rizzo, J. F., Ziv, O. R., Grumet, A., Wyatt, J. Thresholds for activation of rabbit retinal ganglion cells with an ultrafine, extracellular microelectrode. Investigative Ophthalmology and Visual Science. 44 (8), 3533-3543 (2003).
- Kim, W., Choi, M., Kim, S. -W. The normative retinal and choroidal thicknesses of the rabbit as revealed by spectral domain optical coherence tomography. Journal of the Korean Ophthalmological Society. 62 (3), 354-361 (2021).
- Guo, T., et al. Influence of cell morphology in a computational model of ON and OFF retinal ganglion cells. 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). 2013, 4553-4556 (2013).
- Haberbosch, L., et al. Safety aspects, tolerability and modeling of retinofugal alternating current stimulation. Frontiers in Neuroscience. 13, 783(2019).
- Sheasby, B. W., Fohlmeister, J. F. Impulse encoding across the dendritic morphologies of retinal ganglion cells. Journal of Neurophysiology. 81 (4), 1685-1698 (1999).
- Rockhill, R. L., Daly, F. J., MacNeil, M. A., Brown, S. P., Masland, R. H. The diversity of ganglion cells in a mammalian retina. Journal of Neuroscience. 22 (9), 3831-3843 (2002).
- Lukasiewicz, P., Werblin, F. A slowly inactivating potassium current truncates spike activity in ganglion cells of the tiger salamander retina. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience. 8 (12), 4470-4481 (1988).
- Van Rossum, G. Python Reference Manual. , CWI: Centrum voor Wiskunde en Informatica. Amsterdam. (1995).
- Spyder Doc Contributors. Welcome to Spyder's Documentation - Spyder 5 documentation. , Available from: https://docs.spyder-idle.org/current/index.html (2022).
- Rattay, F. Ways to approximate current-distance relations for electrically stimulated fibers. Journal of Theoretical Biology. 125 (3), 339-349 (1987).
- Tsai, D., Morley, J. W., Suaning, G. J., Lovell, N. H. Direct activation and temporal response properties of rabbit retinal ganglion cells following subretinal stimulation. Journal of Neurophysiology. 102 (5), 2982-2993 (2009).
- Tsai, D., Morley, J. W., Suaning, G. J., Lovell, N. H. Frequency-dependent reduction of voltage-gated sodium current modulates retinal ganglion cell response rate to electrical stimulation. Journal of Neural Engineering. 8 (6), 066007(2011).
- Joucla, S., Glière, A., Yvert, B. Current approaches to model extracellular electrical neural microstimulation. Frontiers in Computational Neuroscience. 8, 13(2014).
- OpenFOAM. , Available from: https://www.openfoam.com/ (2022).
- Barba, L., Forsyth, G. CFD Python: The 12 steps to Navier-Stokes equations. Journal of Open Source Education. 1 (9), 21(2018).
Перепечатки и разрешения
Запросить разрешение на использование текста или рисунков этого JoVE статьи
Запросить разрешениеСмотреть дополнительные статьи
This article has been published
Video Coming Soon
Авторские права © 2025 MyJoVE Corporation. Все права защищены