Method Article
Modelado computacional de neuronas retinianas para la investigación de prótesis visuales - Enfoques fundamentales
En este artículo
Resumen
Resumimos un flujo de trabajo para modelar computacionalmente los comportamientos de una neurona retiniana en respuesta a la estimulación eléctrica. El modelo computacional es versátil e incluye pasos de automatización que son útiles para simular una variedad de escenarios fisiológicos y anticipar los resultados de futuros estudios in vivo / in vitro .
Resumen
El modelado computacional se ha convertido en un método cada vez más importante en la ingeniería neuronal debido a su capacidad para predecir comportamientos de sistemas in vivo e in vitro . Esto tiene la ventaja clave de minimizar el número de animales requeridos en un estudio dado al proporcionar una predicción a menudo muy precisa de los resultados fisiológicos. En el campo de la prótesis visual, el modelado computacional tiene una variedad de aplicaciones prácticas, que incluyen informar el diseño de una matriz de electrodos implantables y la predicción de percepciones visuales que pueden obtenerse a través de la entrega de impulsos eléctricos de dicha matriz. Algunos modelos descritos en la literatura combinan una morfología tridimensional (3D) para calcular el campo eléctrico y un modelo de cable de la neurona o red neuronal de interés. Para aumentar la accesibilidad de este método de dos pasos para los investigadores que pueden tener una experiencia previa limitada en el modelado computacional, proporcionamos un video de los enfoques fundamentales que se deben tomar para construir un modelo computacional y utilizarlo para predecir los resultados fisiológicos y psicofísicos de los protocolos de estimulación implementados a través de una prótesis visual. La guía comprende los pasos para construir un modelo 3D en un software de modelado de elementos finitos (FEM), la construcción de un modelo de células ganglionares de la retina en un software computacional de neuronas multicompartimentales, seguido de la fusión de los dos. Un software de modelado de elementos finitos para resolver numéricamente ecuaciones físicas se utilizaría para resolver la distribución del campo eléctrico en las estimulaciones eléctricas del tejido. Luego, se utilizó un software especializado para simular las actividades eléctricas de una célula o red neuronal. Para seguir este tutorial, se requeriría familiaridad con el principio de funcionamiento de una neuroprótesis, así como conceptos neurofisiológicos (por ejemplo, mecanismo de potencial de acción y una comprensión del modelo de Hodgkin-Huxley).
Introducción
Las neuroprótesis visuales son un grupo de dispositivos que administran estimulaciones (eléctricas, de luz, etc.) a las células neuronales en la vía visual para crear fosfenos o sensación de ver la luz. Es una estrategia de tratamiento que ha estado en uso clínico durante casi una década para personas con ceguera permanente causada por enfermedades degenerativas de la retina. Por lo general, un sistema completo incluiría una cámara externa que captura la información visual alrededor del usuario, una fuente de alimentación y una unidad de computación para procesar y traducir la imagen a una serie de pulsos eléctricos, y una matriz de electrodos implantada que interactúa con el tejido neural y entrega los pulsos eléctricos a las células neuronales. El principio de funcionamiento permite colocar una neuroprótesis visual en diferentes sitios a lo largo de la vía visual desde la retina hasta la corteza visual, siempre que esté aguas abajo del tejido dañado. La mayoría de las investigaciones actuales en neuroprótesis visuales se centran en aumentar la eficacia de la estimulación y mejorar la agudeza espacial para proporcionar una visión más natural.
En los esfuerzos por mejorar la eficacia de la estimulación, el modelado computacional ha sido un método rentable y efectivo para validar el diseño de una prótesis y simular su resultado visual. El modelado computacional en este campo ganó popularidad desde 1999 cuando Greenberg1 modeló la respuesta de una célula ganglionar de la retina a estímulos eléctricos extracelulares. Desde entonces, el modelado computacional se ha utilizado para optimizar los parámetros del pulso eléctrico 2,3 o el diseño geométrico del electrodo 4,5. A pesar de la variación en la complejidad y las preguntas de investigación, estos modelos funcionan determinando la distribución del voltaje eléctrico en el medio (por ejemplo, tejido neural) y estimando la respuesta eléctrica que las neuronas en la vecindad producirán debido al voltaje eléctrico.
La distribución de voltaje eléctrico en un conductor se puede encontrar resolviendo las ecuaciones de Poisson6 en todas las ubicaciones:
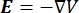
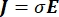
donde E es el campo eléctrico, V el potencial eléctrico, J la densidad de corriente y σ es la conductividad eléctrica. El  en la ecuación indica un operador de gradiente. En el caso de la corriente estacionaria, se imponen las siguientes condiciones de contorno en el modelo:
en la ecuación indica un operador de gradiente. En el caso de la corriente estacionaria, se imponen las siguientes condiciones de contorno en el modelo:


donde n es la normal a la superficie, Ω representa el límite e I0 representa la corriente específica. Juntos, crean aislamiento eléctrico en los límites externos y crean una fuente de corriente para un límite seleccionado. Si asumimos una fuente puntual monopolar en un medio homogéneo con una conductividad isotrópica, el potencial eléctrico extracelular en una ubicación arbitraria se puede calcular por7:

donde Ie es la corriente y es la distancia entre el electrodo y el punto de medición. Cuando el medio no es homogéneo o anisótropo, o la matriz de electrodos tiene múltiples electrodos, una suite computacional para resolver numéricamente las ecuaciones puede ser conveniente. Un software de modelado de elementos finitos6 divide el conductor de volumen en pequeñas secciones conocidas como "elementos". Los elementos están interconectados entre sí de tal manera que los efectos del cambio en un elemento influyen en el cambio en otros, y resuelve las ecuaciones físicas que sirven para describir estos elementos. Con la creciente velocidad computacional de las computadoras modernas, este proceso se puede completar en segundos. Una vez que se calcula el potencial eléctrico, se puede estimar la respuesta eléctrica de la neurona.
Una neurona envía y recibe información en forma de señales eléctricas. Tales señales vienen en dos formas: potenciales graduados y potenciales de acción. Los potenciales graduales son cambios temporales en el potencial de membrana en los que el voltaje a través de la membrana se vuelve más positivo (despolarización) o negativo (hiperpolarización). Los potenciales graduales suelen tener efectos localizados. En las células que los producen, los potenciales de acción son respuestas de todo o nada que pueden viajar largas distancias a lo largo de un axón. Tanto los potenciales graduales como los de acción son sensibles al entorno eléctrico y químico. Un pico de potencial de acción puede ser producido por varios tipos de células neuronales, incluidas las células ganglionares de la retina, cuando se cruza un potencial transmembrana umbral. El potencial de acción y la propagación desencadenan la transmisión sináptica de señales a las neuronas aguas abajo. Una neurona puede ser modelada como un cable que se divide en segmentos cilíndricos, donde cada segmento tiene capacitancia y resistencia debido a la membrana de la bicapa lipídica8. Un programa computacional neuronal9 puede estimar la actividad eléctrica de una célula eléctricamente excitable discretizando la célula en múltiples compartimentos y resolviendo el modelo matemático10:
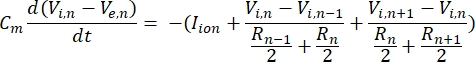
En esta ecuación, Cmes la capacitancia de membrana, V e,n es el potencial extracelular en el nodo n, Vi,n el potencial intracelular en el nodo n, R n la resistencia intracelular (longitudinal) en el nodo n, y el ion I es la corriente iónica que pasa a través de los canales iónicos en el nodo n. Los valores de V del modelo FEM se implementan como Ve,n para todos los nodos de la neurona cuando la estimulación está activa.
Las corrientes transmembrana de los canales iónicos se pueden modelar utilizando formulaciones de Hodgkin-Huxley11:
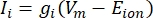
donde g i es la conductancia específica del canal, V m el potencial transmembrana (V i,n - Ve,n) y Eion el potencial de inversión del canal iónico. Para los canales dependientes de voltaje, como el canal Na, se introducen parámetros adimensionales, m y h, que describen la probabilidad de apertura o cierre de los canales:
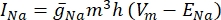
donde  es la conductancia máxima de membrana para el canal iónico particular, y los valores de los parámetros m y h se definen mediante ecuaciones diferenciales:
es la conductancia máxima de membrana para el canal iónico particular, y los valores de los parámetros m y h se definen mediante ecuaciones diferenciales:

donde α x y βx son funciones dependientes del voltaje que definen las constantes de velocidad del canal iónico. Generalmente toman la forma:

Los valores de los parámetros en estas ecuaciones, incluida la conductancia máxima, así como las constantes A, B, C y D, se encontraron típicamente a partir de mediciones empíricas.
Con estos bloques de construcción, se pueden construir modelos de diferentes complejidades siguiendo los pasos descritos. Un software FEM es útil cuando la ecuación de Poisson no se puede resolver analíticamente, como en el caso de conductancia no homogénea o anisotrópica en el conductor de volumen o cuando la geometría de la matriz de electrodos es compleja. Después de que se hayan resuelto los valores de potencial extracelular, el modelo de cable neuronal se puede resolver numéricamente en el software computacional neuronal. La combinación de los dos programas permite el cálculo de una célula neuronal compleja o red a un campo eléctrico no uniforme.
Se construirá un modelo simple de dos pasos de una célula ganglionar retiniana bajo una estimulación supracoroidea utilizando los programas antes mencionados. En este estudio, la célula ganglionar de la retina se someterá a un rango de magnitudes de pulsos de corriente eléctrica. La ubicación de la célula en relación con el estímulo también se varía para mostrar la relación distancia-umbral. Además, el estudio incluye una validación del resultado computacional contra un estudio in vivo del umbral de activación cortical utilizando diferentes tamaños de electrodo de estimulación12, así como un estudio in vitro que muestra la relación entre la distancia electrodo-neurona y el umbral de activación13.
Protocolo
1. Configuración del modelo de elementos finitos para cálculos de potencial eléctrico
- Determinar los pasos de simulación y la complejidad del modelo
NOTA: El objetivo del primer paso es aclarar el propósito del modelado, que determinará los elementos necesarios del modelo y el procedimiento de simulación. Un punto importante a considerar es el comportamiento de las células neuronales que debe ser mostrado por el modelo, y qué protocolo de prueba se necesitaría para demostrar ese comportamiento. Este estudio muestra una relación distancia-umbral para una neurona que es estimulada extracelularmente, así como la curva de tamaño del electrodo-umbral. Para ello, se necesita un modelo de célula neuronal compartimentado en diferentes secciones (para incorporar la variación de parámetros morfológicos y biofísicos en la neurona) sensibles al voltaje extracelular y simulación de un rango de tamaños y posiciones de electrodos.- Definir la pregunta de investigación y las variables experimentales.
- Definir una pregunta de investigación y un protocolo de prueba para guiar la construcción del modelo. Lo mejor es comenzar con una pregunta clara y construir un modelo lo más simple posible para responderla.
- Determinar los elementos necesarios para ser incluidos en el modelo completo
NOTA: En este enfoque de modelado, se considera que la célula está inmersa en un medio eléctricamente conductor, es decir, el tejido biológico. La estimulación eléctrica ocurre a través de este "conductor de volumen", es decir, el medio, lo que resulta en una distribución del potencial eléctrico.- Con base en las preguntas de investigación y las variables a resolver, decida si se requieren ambos elementos (FEM y modelo de cable neuronal). Si, por ejemplo, el modelado necesita un solo electrodo que pueda simplificarse como fuente puntual y que el medio sea homogéneo, un FEM podría no ser necesario, y se puede hacer un cálculo analítico del campo eléctrico extracelular para reemplazarlo.
- Definir la pregunta de investigación y las variables experimentales.
- Descargue e instale el software
NOTA: El estudio utilizó las versiones de aplicaciones de software (COMSOL, NEURON y Python Anaconda) y hardware especificado en la Tabla de materiales. Puede haber pequeñas diferencias en los pasos o resultados si se utilizan diferentes versiones del software/hardware.- Descargue el software que se adapte al sistema operativo de la computadora y compre una licencia, si es necesario. Asegúrese de que todos los módulos de simulación necesarios estén descargados e instale todo el software.
- Recopilar los datos sobre la anatomía del tejido y la célula a modelar
NOTA: Para este método, los parámetros anatómicos y biofísicos se tomaron de los hallazgos empíricos. Es común que los modelos computacionales mezclen parámetros medidos en diferentes especies debido a la falta de disponibilidad de datos. Para una simulación de estimulación supracoroidea, las capas de tejido entre los electrodos estimulantes y de referencia deben incluirse en el modelo.- Reunir la anatomía del tejido a partir de estudios histológicos.
- En este modelo, incluya la coroides, el tejido retiniano y los dominios vítreos, donde cada dominio se modela como un prisma rectangular para facilitar la construcción del modelo. Recoger el espesor medio del tejido retiniano a partir de los datos histológicos publicados14 para posteriormente utilizarlos como altura de cada prisma.
- Recopile los datos de morfología de una sola célula de la tinción celular o de la base de datos pública de neuronas.
- Descargue la morfología detallada de la neurona de una base de datos como NeuroMorpho.org, que proporciona una función de metadatos de búsqueda para encontrar la neurona relevante según la especie, la región del cerebro, el tipo de célula, etc. Para este estudio, encuentre el modelo OFF RGC de Guo (D23WM13_27_1-OffRGC_msa)15 ingresando Conejo > Blanco de Nueva Zelanda en el campo Especies y Retina en el campo Región cerebral . Haga clic en el modelo y descargue el archivo .swc.
- Reunir la anatomía del tejido a partir de estudios histológicos.
- Recopilar los datos biofísicos de la célula modelada
NOTA: Los parámetros biofísicos incluyen los valores de conductividad eléctrica para cada capa de tejido y los parámetros eléctricos de la membrana neural y los canales iónicos.- Debido a la disponibilidad de datos, utilice los valores de conductividad eléctrica que se tomaron del conejo16 para el modelo de tejido, mientras que la dinámica de los canales iónicos se basó en el modelo de Sheasby y Fohlmeister de la retina de la salamandra tigre17.
- Construir la geometría del modelo de elementos finitos del tejido y el electrodo en el software FEM
NOTA: La geometría del tejido y la matriz de electrodos afectan la distribución del potencial eléctrico, lo que a su vez influye en el comportamiento de las células neuronales. Por lo tanto, es importante construir una geometría realista del medio donde residen las células, así como del electrodo. El software FEM utilizado en este tutorial tiene una GUI que permite una fácil construcción de la geometría del modelo.- Configuración del modelo FEM en la interfaz gráfica de usuario del software:
- Ejecute el software FEM y haga clic en Asistente de modelos > 3D. En el cuadro de lista Seleccionar física , expanda AC /DC > Campos eléctricos y corriente > corrientes eléctricas (ec) y, a continuación, haga clic en Agregar. Haga clic en Estudio y agregue un estudio estacionario en la opción Estudios generales , y luego haga clic en Listo (Figura complementaria 1).
- Configuración de la unidad y los parámetros geométricos del electrodo.
- En el árbol del Generador de modelos, haga clic en Parámetros 1. En la tabla, escriba 'elec_rad' en el campo Nombre y '50' en el campo Expresión para crear un electrodo de 50 unidades de radio. Luego, haga clic en Geometría y cambie la unidad de longitud a μm, ya que el soma de una célula ganglionar retiniana típica tiene alrededor de 10 μm de diámetro (Figura complementaria 2).
- Crear las capas de tejido usando dominios de bloque
NOTA: Para construir la geometría del modelo, se utilizaron tres bloques para representar diferentes estructuras en el ojo. El bloque 1 representaba la coroides, el bloque 2 el tejido retiniano y el bloque 3 el vítreo.- Haga clic con el botón derecho en Geometry 1 > Block para crear un dominio de bloque. Repita este paso dos veces más para crear tres bloques en total. Para todos los bloques, establezca Profundidad y Anchura en 5.000 μm, y cambie la opción Base (en Posición) a Centro. Asigne los siguientes valores de altura (en tamaño y forma) y z (en posición) para cada bloque:
Bloque 1: Altura = 112 μm, z = 0 μm
Bloque 2: Altura = 151 μm, z = 131,5 μm
Bloque 3: Altura = 5.000 μm, z = 2.707 μm
- Haga clic con el botón derecho en Geometry 1 > Block para crear un dominio de bloque. Repita este paso dos veces más para crear tres bloques en total. Para todos los bloques, establezca Profundidad y Anchura en 5.000 μm, y cambie la opción Base (en Posición) a Centro. Asigne los siguientes valores de altura (en tamaño y forma) y z (en posición) para cada bloque:
- Creación de un plano de trabajo para agregar un electrodo al modelo
- Haga clic con el botón derecho en la Geometría 1 del árbol del modelo y elija Plano de trabajo. Haga clic en Plano de trabajo 1 y cambie el Tipo de plano a Cara paralela, haga clic en el botón Activar selección debajo del Tipo de plano y elija la superficie inferior del Bloque 1 (blk 1 > 1).
- Dibujo de un electrodo de disco en el plano de trabajo
- Haga clic en Geometría plana en Plano de trabajo 1 y haga clic en Esbozo en la barra de herramientas principal. Seleccione Círculo, haga clic en cualquier lugar dentro del rectángulo en la pestaña Gráficos y arrastre para crear un electrodo de disco. Cambie el radio a 'elec_rad' μm, xw y yw a 0 μm, y luego haga clic en Construir todo.
- Asignación de propiedades de material a cada dominio
NOTA: Siguiendo los pasos para construir la geometría, el modelo se separaría en varios 'dominios', que son partes 3D individuales que componen la geometría completa. A cada dominio se le debe asignar un valor de conductividad eléctrica para calcular la distribución del campo eléctrico en todo el modelo.- En el árbol del modelo, haga clic con el botón derecho en Material > Material en blanco y, a continuación, haga clic en Material 1 y cambie la Selección a Manual.
- Haga clic en los dominios en la ventana Gráficos para que solo se elija el dominio 1. Elija Propiedades del material > Propiedades básicas > Conductividad eléctrica, haga clic en el botón Agregar al material y cambie el valor de conductividad eléctrica al valor a 0.043 S / m15.
- Repita los pasos para los dominios 2 y 3, con los valores de conductividad eléctrica de 0,7 16 y 1,5516 S/m, respectivamente (Figura complementaria 3).
- Mallado de un modelo 3D: Para mallar el modelo, vaya al árbol del modelo y haga clic con el botón derecho en Malla 1 > Tetraédrico libre. Haga clic en Free Tetrahedral 1 y elija Build All.
NOTA: El proceso de mallado divide toda la geometría en "elementos" más pequeños (un elemento es un segmento virtual de la geometría del modelo donde las ecuaciones físicas se resuelven numéricamente). El engranaje con elementos más pequeños teóricamente aumenta la precisión de la aproximación, pero es computacionalmente exhaustivo. Una práctica común es comenzar el modelo con malla dispersa y registrar el resultado de la simulación, luego repetir continuamente la simulación con elementos de malla más pequeños cada vez y comparar los resultados. El proceso de refinamiento puede detenerse cuando no hay una diferencia significativa en los resultados del cálculo de los pasos de refinamiento posteriores.- Evaluación de la calidad de la malla: Haga clic con el botón derecho en Malla 1 y elija Estadísticas para mostrar el histograma de la calidad del elemento. Siga los pasos de refinación de malla a continuación para mejorar la calidad de los elementos.
NOTA: El uso del mallado predeterminado puede producir muchos elementos de baja calidad, lo que a su vez genera cálculos inexactos. En la mayoría de los casos, se necesita cierto grado de refinamiento de la malla. - Refinar la malla alrededor del perímetro del electrodo
NOTA: Las áreas donde podría haber cambios abruptos en el campo eléctrico generalmente requieren una malla más refinada. Aquí, se agregó una malla más densa alrededor del perímetro del electrodo utilizando la función de distribución de bordes.- En primer lugar, elimine la malla tetraédrica libre 1 existente. Luego, haga clic derecho en Malla 1 > Distribución, haga clic en Distribución 1, cambie el Nivel de entidad geométrica a Arista y elija Aristas 19-22 (el perímetro del electrodo de disco).
- Establezca el Tipo de distribución en Número fijo de elementos y cambie el campo Número de elementos a elec_rad*3/10 para que los elementos sean razonablemente pequeños.
- Refinar la malla a través de la coroides y el tejido retiniano
- En el árbol modelo, haga clic con el botón derecho en Malla 1 > Barrido. Haga clic en Barrido 1. Elija los dominios 1 y 2. Luego, haga clic derecho en Malla 1 > Tetraédrico libre, establezca el Nivel de entidad geométrica en Restante y haga clic en Construir todo. (Opcional: Compruebe de nuevo el histograma de calidad del elemento para asegurarse de que los elementos de baja calidad se han reducido en proporción).
- Evaluación de la calidad de la malla: Haga clic con el botón derecho en Malla 1 y elija Estadísticas para mostrar el histograma de la calidad del elemento. Siga los pasos de refinación de malla a continuación para mejorar la calidad de los elementos.
- Configuración del modelo FEM en la interfaz gráfica de usuario del software:
- Aplicar la física al modelo de elementos finitos
NOTA: La 'física' en el software FEM son conjuntos de ecuaciones matemáticas y condiciones de contorno que deben asignarse al modelo. Es el cálculo de la solución al conjunto simultáneo de ecuaciones que se lleva a cabo durante el curso de la ejecución del modelo. La elección de la física a aplicar a la geometría depende del fenómeno físico que se simula. Por ejemplo, la física de la corriente eléctrica, tal como se usa en este modelo, observa la distribución del campo eléctrico y descuida el fenómeno magnético (inductivo). Otra física podría aplicarse a la geometría si se deben resolver otros problemas físicos (por ejemplo, distribución de temperatura, estrés mecánico, etc.).- Selección de la física y aplicación de las condiciones de contorno
NOTA: Si se va a aplicar un pulso de voltaje constante, la condición de límite de potencial flotante debe reemplazarse con una condición de límite de potencial eléctrico.- Expanda Corrientes eléctricas 1 en el árbol modelo y compruebe si aparecen los valores Conservación de corriente 1, Aislamiento eléctrico 1 y Valores iniciales 1 . Luego, haga clic derecho en Corrientes eléctricas 1 > Tierra (esto asigna 0 V a un plano distante, simulando un electrodo de referencia distante) y aplíquelo a la superficie más alejada del electrodo (Superficie 10).
- A continuación, haga clic con el botón derecho en Corrientes eléctricas 1 > potencial flotante (esto simula una fuente de corriente con corriente constante), asignado al electrodo de disco (superficie 14), y cambie el valor I 0 a 1 [μA] para aplicar una corriente unitaria.
- Ejecutar la simulación con un barrido paramétrico.
NOTA: Este paso ejecutará la simulación y se agregó un barrido paramétrico, donde se realizaron varias simulaciones con el valor de un parámetro cambiado en cada simulación. Aquí, se barrió el parámetro del radio del electrodo y la distribución del potencial eléctrico para cada simulación se almacenó en el archivo del modelo. Después de ejecutar la simulación, la rama Resultados del árbol modelo se rellenó con un gráfico multicorte de potencial eléctrico (ec).- En el árbol modelo, haga clic con el botón derecho en Estudio 1 > Barrido paramétrico. Haga clic en Barrido paramétrico y, en la tabla Configuración del estudio , haga clic en Agregar y, a continuación, elija elec_rad para el Nombre del parámetro.
- Escriba '50, 150, 350, 500' para la Lista de valores de parámetros y 'μm' para la Unidad de parámetros, y haga clic en Calcular para ejecutar el estudio (Figura complementaria 4).
- Selección de la física y aplicación de las condiciones de contorno

Figura 1: Creación de la geometría de tisssue. Se insertó una geometría de bloque en el modelo FEM para representar el tejido. Haga clic aquí para ver una versión más grande de esta figura.
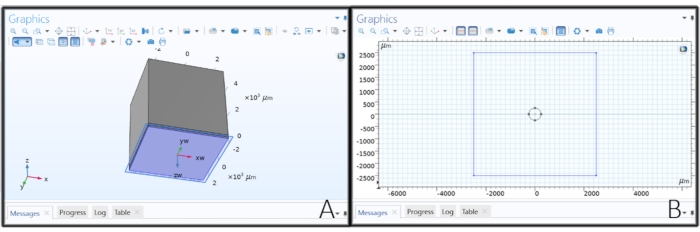
Figura 2: Creación de la geometría del electrodo. (A) Hacer un plano de trabajo para dibujar el electrodo de disco. (B) Dibujar un círculo en un plano de trabajo para crear un electrodo de disco. Haga clic aquí para ver una versión más grande de esta figura.

Figura 3: El histograma de calidad del elemento del modelo FEM. El histograma mostró la calidad de los elementos en todo el modelo. Se necesitan refinamientos de malla si una parte significativa de los elementos se encuentran en la región de baja calidad. Haga clic aquí para ver una versión más grande de esta figura.
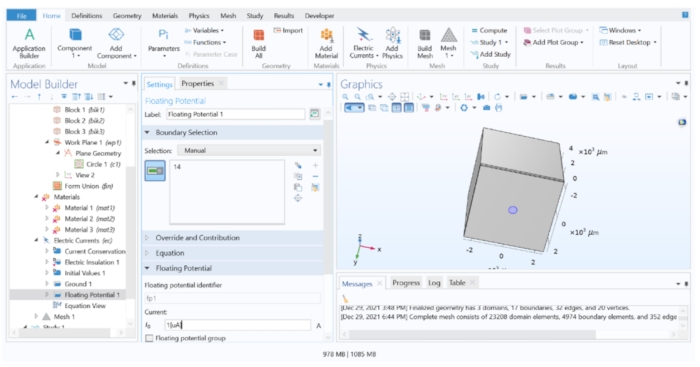
Figura 4: Asignación de un valor de corriente al electrodo. Una corriente unitaria aplicada a la geometría del electrodo en el software FEM. Haga clic aquí para ver una versión más grande de esta figura.
2. Importación de la geometría de la célula neuronal en la GUI de la suite computacional neuronal
- Construir la geometría del modelo de celda
- Importación de la morfología mediante la función Cell Builder.
- Ejecute 'nrngui' desde la carpeta de instalación de la suite computacional neuronal, haga clic en Herramientas > Varios > Importar 3D y luego marque la casilla Elegir un archivo .
- Localice el archivo .swc descargado y haga clic en Leer. Una vez importada la geometría, haga clic en Exportar > Cell Builder (Figura complementaria 5).
- Creación de un archivo .hoc de la morfología de celda importada
- Vaya a la pestaña Subconjuntos y observe los subconjuntos que se han predefinido en el modelo (por ejemplo, soma, axón, basal, etc.). Marque la casilla Crear continuo , vaya a Administración > Exportar y exporte la morfología como 'rgc.hoc'.
- Visualización de la morfología de la célula
- Haga clic en Vista de herramienta > modelo > 1 Celdas reales > Root Soma[0] en la barra de herramientas, haga clic con el botón derecho en la ventana que aparece y haga clic en Tipo de eje > Ver eje. Mediante inspección visual, el diámetro del campo dendrítico de este modelo es de alrededor de 250 μm. Cierre las ventanas de NEURON por ahora.
- Importación de la morfología mediante la función Cell Builder.

Figura 5: Exportación de la información del modelo neuronal como un archivo .hoc. La geometría de la neurona se exportó a un archivo .hoc para permitir más modificaciones. Haga clic aquí para ver una versión más grande de esta figura.
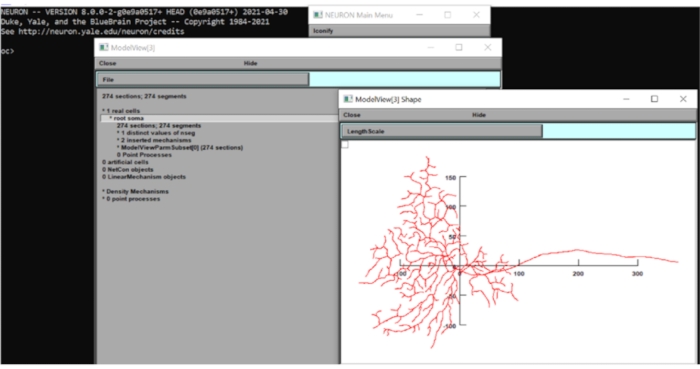
Figura 6: Medición de la dimensión de la neurona. La morfología de la neurona (vista superior) se mostró en la GUI del conjunto computacional neuronal con los ejes x-y superpuestos. La escala estaba en μm. Haga clic aquí para ver una versión más grande de esta figura.
3. Programación de la simulación computacional NEURON
- Ajuste de la morfología de la célula mediante programación en lenguaje .hoc
NOTA: La morfología de la celda se puede ajustar a través de la función Cell Builder de la GUI. Sin embargo, se demuestra cómo se podría hacer esto editando el archivo .hoc para acelerar el proceso. El archivo .hoc define la topología (conexiones físicas entre cada parte de las neuronas), la morfología (la longitud, el diámetro y la ubicación de cada sección neuronal) y las propiedades biofísicas (parámetros del canal iónico) de la célula modelada. La documentación completa para la programación .hoc se puede encontrar en: https://neuron.yale.edu/neuron/static/new_doc/index.html#,- Abra el archivo .hoc resultante con un editor de texto (por ejemplo, el Bloc de notas). Agregue un segmento inicial del axón de 40 μm de longitud y un segmento axonal estrecho de 90 μm de longitud cerca del soma como se describe en Sheasby y Fohlmeister17, así como cambie la longitud de las dendritas para que el tamaño del campo dendrítico se convierta en 180 μm para que coincida con la célula G1 en Rockhill, et al.18.
- Creación de nuevas secciones de celda y definición de las conexiones topológicas para cada sección.
- Para crear nuevas secciones de celda para el segmento inicial del axón (AIS) y el segmento axonal estrecho (NS), agregue estas líneas al principio del archivo rgc.hoc:
crear AIS, NS // Declarar compartimentos celulares llamados AIS y NS
A continuación, sustituya la línea «conectar axón(0), soma[1](1)» por:
conectar ais(0), soma[1](1) // Conectando el primer segmento de AIS al final de soma[1]
connect ns(0), ais(1) // Conectando el primer segmento de NS al final de AIS
conectar axón(0), ns(1) // Conectar el primer segmento del axón al final de NS
- Para crear nuevas secciones de celda para el segmento inicial del axón (AIS) y el segmento axonal estrecho (NS), agregue estas líneas al principio del archivo rgc.hoc:
- Definición de las posiciones 3D, los diámetros y la longitud de las secciones de celda
- Defina las posiciones y diámetros 3D de los compartimentos AIS y NS escribiendo estas líneas dentro de los corchetes 'proc shape3d_31()':
ais { pt3dadd(-2.25, -1.55, 0, 1) // Los tres primeros números son la coordenada xyz, y el diámetro es 1 μm
pt3dadd(37.75, -1.55, 0, 1)} // El primer punto está en x = -2.25 μm y el último punto está en x = 37.75 μm
ns { pt3dadd(37.75, -1.55, 0, 0.3) // Las coordenadas 3D y el diámetro de los segmentos NS
pt3dadd(127.75, -1.55, 0, 0.3)} - Al final del archivo, cambie la coordenada 3D del axón para que su punto inicial se encuentre con el punto final de NS escribiendo:
axon {for i=0,n3d()-1 {pt3dchange(i, x3d(i)+130, y3d(i),z3d(i)-5, diam3d(i))}} //Shift the x-coordinate - Al final del archivo, acorte los compartimentos dendríticos en un 18% escribiendo:
forsec basal {L=L*0.82} // Escalar la longitud para reducir el tamaño del campo dendrítico
define_shape() // Relleno de la información 3D que falta
- Defina las posiciones y diámetros 3D de los compartimentos AIS y NS escribiendo estas líneas dentro de los corchetes 'proc shape3d_31()':
- Creación de nuevas secciones de celda y definición de las conexiones topológicas para cada sección.
- Abra el archivo .hoc resultante con un editor de texto (por ejemplo, el Bloc de notas). Agregue un segmento inicial del axón de 40 μm de longitud y un segmento axonal estrecho de 90 μm de longitud cerca del soma como se describe en Sheasby y Fohlmeister17, así como cambie la longitud de las dendritas para que el tamaño del campo dendrítico se convierta en 180 μm para que coincida con la célula G1 en Rockhill, et al.18.
- Definición del número de segmentos para cada sección
NOTA: Cada sección de la neurona se puede discretizar espacialmente, al igual que el proceso de mallado en el modelo FEM. La discretización espacial divide la neurona virtualmente en segmentos más pequeños donde se deben realizar cálculos. Para el número de segmentos 'nseg', asegúrese de que se utilizan números impares para garantizar que haya un nodo interno en el punto medio de una sección de celda, e intente triplicar el número nseg hasta que el cálculo produzca un resultado consistente9. Un mayor número de segmentos producirá una aproximación numérica más precisa, pero también aumenta la carga computacional.- Para ejemplificar el proceso de discretización, agregue las siguientes líneas en el archivo rgc.hoc para dividir las secciones neuronales en los subconjuntos somático y axonal en varios segmentos:
Forsec somático {nseg=31}
Forsec axonal {nseg=301}
Otras secciones en el modelo también deben discretizarse escribiendo estas líneas pero cambiando el nombre del subconjunto (después de 'forsec') y el número de segmentos (después de 'nseg') como se desee.
- Para ejemplificar el proceso de discretización, agregue las siguientes líneas en el archivo rgc.hoc para dividir las secciones neuronales en los subconjuntos somático y axonal en varios segmentos:
- Insertar mecanismos de canal iónico personalizados
- Escribir mecanismos de canal iónico personalizados como archivos .mod: Para aplicar los mecanismos del canal iónico, cree archivos .mod e inserte los archivos en la parte de la sección biofísica del archivo .hoc siguiendo los pasos 3.3.1-3.3.3. El archivo .mod contiene las variables y las ecuaciones diferenciales a resolver para cada canal iónico.
NOTA: Las definiciones e implementaciones correctas del mecanismo del canal iónico son críticas en simulaciones neuronales precisas. Al escribir archivos .mod, compruebe si las unidades son correctas (la utilidad 'modlunit' proporcionada que se puede ejecutar para comprobar la consistencia de la unidad) y que las ecuaciones se escriben correctamente. Para probar que los mecanismos del canal iónico son correctos, se puede trazar la corriente para cada canal iónico durante la estimulación intracelular o extracelular y compararla con los hallazgos empíricos.- Canales iónicos dependientes de voltaje
NOTA: Un archivo .mod para crear un canal iónico dependiente de voltaje normalmente incluye un bloque DERIVATIVE que tiene la ecuación diferencial para resolver, un bloque BREAKPOINT que tiene los comandos para resolver las ecuaciones diferenciales utilizando un método de aproximación numérica elegido y bloques PROCEDURE que le dicen al programa que calcule los parámetros de compuerta (por ejemplo, mt, ht y d en este ejemplo). Este código calculará los valores de la corriente iónica que pasa a través del canal para cada paso de tiempo.- Para ejemplificar el proceso, cree un canal de Ca dependiente del voltaje que tenga ecuaciones diferenciales de primer orden para resolver las variables de compuerta.
- Abra un nuevo archivo en el editor de texto y escriba las líneas en el Material suplementario: definición de un canal Cat dependiente del voltaje. Guarde este archivo como Cat.mod en la misma carpeta que el archivo .hoc. Este proceso debe repetirse para los otros canales iónicos que contiene la neurona modelo.
- Canales iónicos dependientes del voltaje y la concentración
- La cinética de algunos canales iónicos, como los canales de potasio activados por calcio en las células ganglionares de la retina, depende de la concentración intracelular de calcio además del voltaje transmembrana19. Para modelar este tipo de mecanismo, cree un archivo llamado KCa.mod y escriba las líneas como se muestra en Canales iónicos suplementarios dependientes del material: voltaje y concentración. En este archivo .mod, se calculó la variable 'cai', que se define como la concentración interna de iones Ca, y luego esta variable se usa en la ecuación para calcular la corriente iKCa.
- Canales iónicos dependientes de voltaje
- Compilación de archivos .mod
- Compile todos los archivos .mod ejecutando la utilidad mknrndll de la suite computacional neuronal desde la carpeta de instalación. Busque la carpeta donde se encuentran los archivos .mod y haga clic en compilar para crear archivos O y C. Después de esto, los mecanismos se pueden insertar en este modelo celular.
- Aplicación de los archivos .mod en el archivo principal del modelo NEURON.
NOTA: Además de insertar los canales iónicos, la conductancia máxima de Na se definió solo para el subconjunto "somático". Podríamos ajustar individualmente la conductancia máxima de la membrana para diferentes segmentos neuronales si fuera necesario.- Para mayor brevedad, combine todos los mecanismos del canal iónico en un solo archivo .mod (archivo .mod de material suplementario-completo). Inserte el archivo .mod combinado que contiene todos los canales iónicos y un canal de fuga pasivo en todos los segmentos del subconjunto 'somático' escribiendo las líneas siguientes en el procedimiento 'biophys' del archivo rgc.hoc:
forsec somatic {insert rgcSpike
insertar PAS // Canal de fuga pasivo
gnabar_rgcSpike = 80e-3
g_pas = 0.008e-3 // conductancia de la membrana de fuga}
- Para mayor brevedad, combine todos los mecanismos del canal iónico en un solo archivo .mod (archivo .mod de material suplementario-completo). Inserte el archivo .mod combinado que contiene todos los canales iónicos y un canal de fuga pasivo en todos los segmentos del subconjunto 'somático' escribiendo las líneas siguientes en el procedimiento 'biophys' del archivo rgc.hoc:
- Ajuste de la resistividad axoplásmica
- Las células tienen resistividad axoplásmica que se puede cambiar por compartimento. Para este modelo, todos los segmentos tienen la misma resistividad de 110 Ω·cm. Cambie la resistividad axoplásmica en el archivo rgc.hoc:
forall {Ra = 110}
- Las células tienen resistividad axoplásmica que se puede cambiar por compartimento. Para este modelo, todos los segmentos tienen la misma resistividad de 110 Ω·cm. Cambie la resistividad axoplásmica en el archivo rgc.hoc:
- Escribir mecanismos de canal iónico personalizados como archivos .mod: Para aplicar los mecanismos del canal iónico, cree archivos .mod e inserte los archivos en la parte de la sección biofísica del archivo .hoc siguiendo los pasos 3.3.1-3.3.3. El archivo .mod contiene las variables y las ecuaciones diferenciales a resolver para cada canal iónico.
- Insertar mecanismos extracelulares y definir la forma de onda del pulso
- Inserción de un mecanismo extracelular en el modelo celular
- Para que el modelo de celda responda al voltaje extracelular, inserte un mecanismo extracelular en todos los segmentos escribiendo la línea en la parte inferior del archivo rgc.hoc:
forall {insertar extracelular}
- Para que el modelo de celda responda al voltaje extracelular, inserte un mecanismo extracelular en todos los segmentos escribiendo la línea en la parte inferior del archivo rgc.hoc:
- Creación de un pulso bifásico
NOTA: En esta demostración, se realiza un pulso bifásico de corriente constante ajustable por el usuario en cuanto al ancho de pulso, el intervalo de interfase y el número de repeticiones mediante la creación de un procedimiento en un archivo .hoc. Para un programa más estructurado, use el archivo rgc.hoc como un archivo para crear el modelo celular, mientras que el proceso de estimulación se aplica en un archivo .hoc separado, que cargaría el modelo celular al que se aplica la estimulación.- Cree un nuevo archivo de texto llamado stimulation.hoc e inicie el código cargando el archivo de modelo de celda; luego, haga un pulso bifásico definiendo un procedimiento como se muestra en Material suplementario-Creación de un pulso bifásico en la simulación neuronal.
NOTA: Este paso crea un pulso catódico catódico de corriente constante donde los parámetros de estímulo deben ser declarados por el usuario al ejecutar la simulación. Actualmente, la magnitud de los pulsos anódico y catódico es de ±1 μA, pero esta magnitud debe cambiar dependiendo de la corriente de estimulación suministrada por el electrodo de disco.
- Cree un nuevo archivo de texto llamado stimulation.hoc e inicie el código cargando el archivo de modelo de celda; luego, haga un pulso bifásico definiendo un procedimiento como se muestra en Material suplementario-Creación de un pulso bifásico en la simulación neuronal.
- Inserción de un mecanismo extracelular en el modelo celular
4. Ejecución y automatización de múltiples simulaciones
- Combinando los modelos
- Extracción de las coordenadas de los nodos en el modelo de células neuronales
NOTA: El propósito de combinar las simulaciones es adquirir los valores de potencial extracelular correspondientes a cada nodo del modelo celular. Sin embargo, las coordenadas de los dos modelos deben estar alineadas. En este ejemplo, el segmento central del soma (soma (0.5)) se alineó para estar en el plano medio horizontal del tejido retiniano (correspondiente a la capa de células ganglionares de la retina), con el nodo central del soma ubicado justo encima del centro del electrodo de disco.- Abra el modelo FEM y observe la coordenada de un punto de referencia (por ejemplo, el plano medio horizontal del tejido retiniano, por encima del centro del electrodo de disco), en cuyo caso es [0, 0, 131.5] μm.
- En el conjunto computacional de neuronas, cree un archivo llamado calculateCoord.hoc para extraer las coordenadas del centroide de cada segmento y desplazar cada sección para que el segmento central del soma tenga la misma coordenada que el punto de referencia en el modelo FEM (Supplementary Material-Calculation the coordinate of each node).
- Guardar los puntos de coordenadas en un archivo de texto
- Ejecute el archivo calculateCoord.hoc (ya sea haciendo doble clic desde el Explorador de archivos o abriendo la GUI de la suite computacional neuronal; luego, haga clic en Archivo > cargar hoc en la barra de herramientas). Guarde las coordenadas de los valores de voltaje extracelular que se evaluarán en un archivo de texto denominado 'coordenadas.dat'.
- Ejecutar las simulaciones y guardar los datos de voltaje en un archivo de texto
NOTA: En este paso, extrajimos los valores extracelulares calculados del modelo FEM, pero solo guardaríamos los datos de las coordenadas relevantes que coinciden con el centro de cada segmento celular. Siga el paso 4.1.6.2 cuando se requiera un gran número de potenciales para exportar.- Abra el archivo de modelo de tejido en el software FEM; vaya al encabezado Resultados en el árbol del modelo y haga clic en Exportar datos > > datos 1. Asegúrese de que el conjunto de datos está establecido en Study 1/Parametric Solutions 1 y, a continuación, escriba 'V' en la columna Expresión y 'mV' en la columna Unidad .
- En Salida, cambie el nombre de archivo a extracelular.dat y elija Puntos para evaluar en: Desde archivo. Cargue las coordenadas.dat para el campo Archivo de coordenadas y, a continuación, haga clic en Exportar.
- Aplicación del pulso bifásico al modelo celular
NOTA: En esta etapa, los valores de voltaje extracelular para cada segmento de celda en un punto de tiempo (donde la corriente es de 1 μA) están disponibles. Como el estudio pretende someter a la célula a un pulso bifásico, hacer que el valor de voltaje extracelular experimentado por la célula cambie con el tiempo utilizando el método 'vector.play'.- Añadir las líneas mostradas en el Material Suplementario-Aplicación del pulso bifásico en el stimulation.hoc.
- Ejecución de la simulación combinada
NOTA: Es necesario definir un intervalo de tiempo 'dt' para las aproximaciones numéricas para ejecutar las simulaciones. Similar a nseg, un dt más corto puede aumentar la precisión computacional, pero también aumenta el costo computacional.- Agregue las líneas que se muestran en la simulación de Ejecución de material suplementario de la neurona al final de la estimulación.hoc. A continuación, haga doble clic en el archivo stimulation.hoc para cargar el script y ejecutar automáticamente la simulación. El potencial transmembrana del segmento de interés puede mostrarse en la GUI del conjunto computacional neuronal (paso 4.2.1) o guardarse en un archivo de texto para ser leído en otros programas (paso 4.1.6.1.2). Siga los pasos 4.1.6.1 y 4.1.6.2 si es necesario exportar cálculos repetidos y un gran número de potenciales de membrana.
- Extra: Automatización de simulaciones
NOTA: Para encontrar una amplitud umbral, haga un bucle de la simulación varias veces con una amplitud de corriente diferente cada vez. Otra automatización podría ser necesaria para encontrar el umbral para las neuronas ubicadas en diferentes posiciones en relación con el electrodo estimulante. Se puede realizar un paso de automatización en la suite computacional neuronal utilizando un procedimiento, así como en el software FEM utilizando un script llamado "método".- Automatización de la simulación neuronal para encontrar un umbral de amplitud
NOTA: Un lote de simulaciones neuronales se puede hacer automáticamente. Los siguientes pasos se implementan en el programa de simulación de neuronas para encontrar las amplitudes umbral de las neuronas bajo diferentes parámetros de estimulación.- Cree un procedimiento para repetir la simulación en el programa de simulación neuronal: En el archivo stimulation.hoc, cree un vector que contenga un rango de amplitud de corriente para probar. Luego, cree un procedimiento para aplicar la amplitud de corriente y registrar cualquier presencia de un pico (un cambio positivo de un voltaje transmembrana negativo a uno positivo), y la amplitud umbral se define como la amplitud de corriente más baja que causa que ocurra un pico. Para ello, defina un procedimiento llamado findTh() (SupplementMaterial-Looping over a range of current amplitudes) al final del archivo stimulation.hoc
- Guardar la respuesta en el umbral en un archivo de texto: Agregue las siguientes líneas al procedimiento findTh() en el archivo stimulation.hoc para almacenar los valores de voltaje transmembrana calculados para todos los compartimentos neuronales de cada paso de tiempo en un archivo de texto:
sprint(saveFileName, "Response_%d.dat", th) // Almacenar el valor del umbral
saveFile.wopen(saveFileName)
para i=0,(responseVector.size()-1){
saveFile.printf("%g, ", responseVector.x[i])
if(i==responseVector.size()-1) {saveFile.printf("%g\n", responseVector.x[i])
saveFile.close(saveFileName)
}}
- Automatización en el software FEM para encontrar los valores de voltaje para neuronas en diferentes ubicaciones
NOTA: Otra automatización que se puede hacer es la adquisición automática de valores de voltaje extracelular para neuronas en diferentes ubicaciones. El menú Application Builder en el software FEM proporciona un medio para definir un 'método', o un script para automatizar los pasos necesarios para que el software realice cálculos. Para demostrarlo, la ubicación de la celda en la dirección x se desplaza 5 veces en un paso de 100 μm (Figura suplementaria 6).- Escribir un código para automatizaciones de simulaciones FEM.
- Vaya a Application Builder, haga clic con el botón derecho en Métodos en el árbol de Application Builder, elija Nuevo método y haga clic en Aceptar. Vaya a Preferencias > métodos de > archivo, marque la casilla Ver todos los códigos y haga clic en Aceptar.
- Escriba un script .hoc que cargue el archivo de coordenadas, cambie los valores para que coincidan con la ubicación deseada y guarde un archivo de texto que contenga los valores de voltaje para la nueva ubicación de la celda escribiendo los códigos que se muestran en el método Definición de material suplementario para automatizar simulaciones FEM.
- Ejecución de los pasos automatizados en el software FEM: Cambie al método Model Builder, Developer > Run > Method 1. Esto producirá archivos .dat con los valores de voltaje apropiados, llamados extracellular_1.dat, extracellular_2.dat, etc.
- Escribir un código para automatizaciones de simulaciones FEM.
- Bucle de las simulaciones en un lenguaje de programación de propósito general
NOTA: Para repetir las simulaciones, el archivo de texto apropiado debe cargarse en la simulación de la suite computacional neuronal cada vez, y un lenguaje de programación20 que pueda cargar y manipular archivos de texto fácilmente es conveniente para realizar este paso. Para este paso se puede utilizar cualquier entorno de desarrollo integrado (IDE)21 conveniente.- Abra el IDE elegido, haga clic en Nuevo archivo para crear un nuevo script. Aquí se utiliza un archivo .py en este ejemplo. Escriba las líneas que se muestran en Material suplementario-Ejecución de las simulaciones en un lenguaje de programación de propósito general.
- Finalmente, haga clic en Ejecutar o presione F5 para ejecutar el script, que también abrirá la GUI (Figura complementaria 7).
- Automatización de la simulación neuronal para encontrar un umbral de amplitud
- Extracción de las coordenadas de los nodos en el modelo de células neuronales
- Visualización de datos de simulación
NOTA: Siguiendo todos los pasos anteriores, los resultados de la simulación deben almacenarse en archivos de texto, que contienen el valor umbral y el potencial transmembrana en el umbral. Sin embargo, el usuario tiene la opción de mostrar el resultado de la simulación mientras la simulación se ejecuta utilizando la GUI de NEURON.- Grafique la respuesta del modelo neuronal a la estimulación extracelular en la GUI de la suite computacional neuronal. Para hacer esto, ejecute stimulation.hoc, haga clic en Gráfico > eje de voltaje en la barra de herramientas y, en la ventana del gráfico, haga clic derecho en cualquier lugar y elija Trazar qué.
- Escriba 'axon.v(1)' en el campo Variable a gráfico , lo que significa que trazará el potencial transmembrana del último segmento del axón por paso de tiempo.
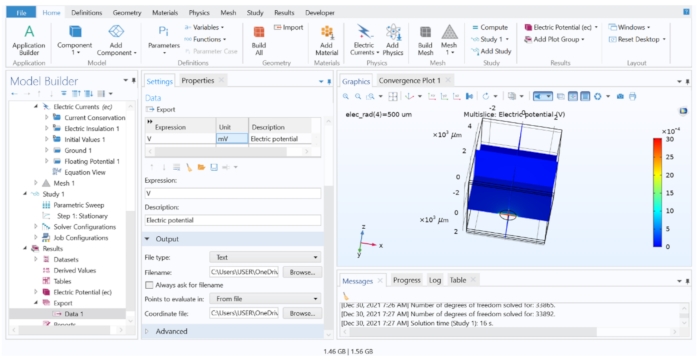
Figura 7: Visualización y exportación de los resultados del cálculo FEM a un archivo de texto. La ventana gráfica muestra un gráfico multicorte del potencial eléctrico en V. Las opciones de la configuración de exportación de datos permitían exportar la variable calculada a un archivo de texto. Haga clic aquí para ver una versión más grande de esta figura.
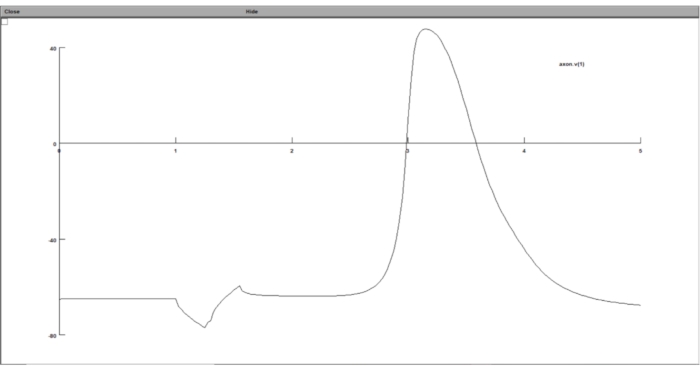
Figura 8: Visualización del gráfico del potencial transmembrana utilizando un gráfico de voltaje. El potencial transmembrana neuronal se mostró en la GUI del conjunto computacional neuronal. El eje x es el tiempo en ms, mientras que el eje y es el potencial transmembrana del segmento neuronal elegido en mV. Haga clic aquí para ver una versión más grande de esta figura.
Resultados
Realizamos dos protocolos de simulación para demostrar el uso del modelo. El primer protocolo consistía en variar el tamaño del electrodo mientras se mantenía la ubicación de la neurona y los parámetros del pulso eléctrico iguales. El segundo protocolo consistió en desplazar la neurona en la dirección x en pasos de 100 μm, mientras que el tamaño del electrodo se mantuvo constante. Para ambos protocolos, el pulso utilizado fue un único pulso catódico bifásico de 0,25 ms de ancho con un intervalo de interfase de 0,05 ms. Para el primer protocolo, el radio del electrodo se varió para ser 50, 150, 350 y 500 μm, mientras que para el segundo protocolo, el radio del electrodo se mantuvo en una constante de 50 μm.
El modelo descrito aquí mostró que el aumento del tamaño del electrodo supracoroideo a 0,25 ms de ancho de pulso aumentó el umbral de activación de la neurona modelo (Figura 9A). Este resultado reflejó los hallazgos in vivo de Liang et al.12, quienes mostraron que el umbral de activación cortical aumenta con el aumento del tamaño del electrodo en este ancho de pulso.
Las magnitudes de los umbrales de activación del modelo difieren de los hallazgos empíricos debido a varios factores. En primer lugar, este modelo solo involucra un único RGC de un tipo específico, que puede no estar presente en el grupo de células que se activan en el estudio in vivo . A continuación, este modelo no incluyó una red retiniana, que puede facilitar la activación de CGR a través de entradas excitatorias de las células bipolares. Otra posible razón para la discrepancia es la distancia electrodo-retina. Es posible que la distancia electrodo-retina en el estudio in vivo fuera menor que en este modelo debido a la variabilidad anatómica o a la cirugía. En consecuencia, sobreestimamos la distancia electrodo-retina y, por lo tanto, el umbral de activación. También es importante tener en cuenta que, aunque esto no se demostró en nuestros resultados, modelar un umbral de una sola célula a menudo subestimaría el umbral cortical in vivo . Esto se debe a las limitaciones técnicas en las mediciones corticales (principalmente relacionadas con la relación señal-ruido) que la actividad cortical generalmente solo se detecta después de que se hayan activado múltiples células ganglionares de la retina. Como resultado, se espera una discrepancia en la magnitud de los umbrales de activación retiniana y cortical. A pesar de estas diferencias, este modelo mostró con éxito la tendencia creciente del umbral de activación debido al aumento en el tamaño del electrodo. Esto resultó de la ausencia de un área de alto campo eléctrico en comparación con su entorno cuando el tamaño del electrodo está aumentado, lo que no favoreció la activación neuronal22.
A continuación, observamos las características del potencial de acción para validar el modelo aquí descrito. La latencia, o el tiempo entre el inicio del estímulo y el pico del pico del potencial de acción, varió de 1 a 2,2 ms (Figura 9B). Esto correspondió al pico de latencia corta debido a la activación retiniana no mediada por la red23. El ancho de la espiga de este modelo fue de 1 ms, y esto está en el mismo rango que los anchos de espiga de las CGR de conejo medidas in vitro24.
En el segundo protocolo de estimulación, solo se varió la ubicación de la neurona en el eje x (a lo largo de la longitud del axón) en relación con el electrodo. A una distancia 0, el centroide de la sección soma estaba inmediatamente por encima del centro del electrodo de disco. La distancia negativa significa que el electrodo de disco se colocó más cerca del lado axonal, mientras que la distancia positiva significa que el electrodo de disco se colocó más cerca del lado dendrítico. El modelo mostró que el umbral más bajo se alcanzó cuando el segmento estrecho del axón estaba inmediatamente por encima del electrodo de disco, y aumentó a medida que la distancia x se hizo más grande (Figura 9C). Mover el electrodo más hacia el axón distal produjo un umbral más bajo en comparación con mover el electrodo hacia las dendritas debido a la presencia del segmento inicial del axón y el segmento estrecho donde los canales de sodio son más frecuentes. Este resultado concuerda con el hallazgo in vitro de Jensen et al.13, donde las CGR de conejo fueron estimuladas con un microelectrodo ultrafino, y el umbral de activación fue el más alto cuando el electrodo se desplazó más cerca de las dendritas.

Figura 9: Los resultados del método de modelado . (A) Los umbrales de activación para una célula ganglionar retiniana ubicada por encima del electrodo de disco. El radio del electrodo fue variado (50, 150, 350 y 500 μm) y el umbral aumentó con el aumento del tamaño del electrodo. (B) La forma potencial de acción del modelo neuronal a 0,25 ms de ancho de pulso. Los potenciales de acción en el umbral para diferentes tamaños de electrodos tienen el mismo ancho de pico de 1 ms, pero la latencia aumentó con el aumento del tamaño del electrodo. El tiempo de inicio del estímulo fue de 1 ms y la fase catódica causó una despolarización en la membrana, pero no lo suficiente como para causar un potencial de acción. (C) La neurona se desplazó a lo largo del eje x y los umbrales de activación mostraron que el umbral más bajo fue alcanzado por la neurona cuyo soma estaba ubicado justo encima del centro del electrodo. El radio del electrodo era de 50 μm. Haga clic aquí para ver una versión más grande de esta figura.
Figura complementaria 1: Inicialización del modelo de elementos finitos. Los tipos de Estudio y Física determinan la lista de ecuaciones resueltas en el modelo. Estos se establecieron durante la creación inicial del archivo de modelo FEM, pero también se pueden modificar/agregar después de que se haya creado el modelo. Haga clic aquí para descargar este archivo.
Figura complementaria 2: Cambio de la unidad de longitud. La unidad de longitud y la unidad angular determinan las unidades utilizadas en el proceso de definición de geometría. Haga clic aquí para descargar este archivo.
Figura complementaria 3: Inserción de una propiedad material. Las propiedades del material se definieron para cada dominio en un modelo 3D. Las propiedades de material disponibles se enumeran en Propiedades de material en la ventana Configuración de material. Para el cálculo del potencial eléctrico, sólo se definió la propiedad de conductividad eléctrica. Haga clic aquí para descargar este archivo.
Figura complementaria 4: Creación de un estudio paramétrico para recorrer una lista de valores de parámetros. Un estudio paramétrico permitió que el software FEM repitiera automáticamente los cálculos y cambiara el valor del radio del electrodo para cada repetición. Los resultados del cálculo se almacenaron para cada repetición. Haga clic aquí para descargar este archivo.
Figura complementaria 5: Importación de la morfología neuronal desde el archivo SWC. La suite computacional neuronal era capaz de leer archivos SWC adquiridos del trazado neuronal. El archivo importado contiene información sobre la morfología y topología de cada segmento neuronal. Haga clic aquí para descargar este archivo.
Figura complementaria 6: Automatización de operaciones FEM mediante la definición de un método. Un método se definió escribiendo un script para automatizar procesos en el software FEM que no se puede hacer definiendo un estudio paramétrico. Haga clic aquí para descargar este archivo.
Figura complementaria 7: Integración de los modelos y automatización de las simulaciones utilizando un lenguaje de programación de propósito general. El lenguaje de programación de propósito general se utilizó para hacer un bucle en las simulaciones neuronales, mientras cambiaba el archivo de voltaje extracelular utilizado como entrada y el archivo de voltaje de respuesta neuronal como salida para cada paso del bucle. Haga clic aquí para descargar este archivo.
Material complementario: Líneas de comando para (1) Definición de un canal Cat dependiente del voltaje. (2) Canales iónicos dependientes del voltaje y la concentración. (3) Archivo .mod completo. (4) Creación de un pulso bifásico en la simulación neuronal. (5) Cálculo de la coordenada de cada nodo. (6) Aplicación del pulso bifásico. (7) Ejecución de la simulación neuronal. (8) Bucle en un rango de amplitudes de corriente. (9) Definición de un método para automatizar simulaciones FEM. (10) Ejecutar las simulaciones en un lenguaje de programación de propósito general. Haga clic aquí para descargar este archivo.
Discusión
En este documento, hemos demostrado un flujo de trabajo de modelado que combina elementos finitos y modelado de neuronas biofísicas. El modelo es altamente flexible, ya que puede modificarse en su complejidad para adaptarse a diferentes propósitos, y proporciona una forma de validar los resultados contra los hallazgos empíricos. También demostramos cómo parametrizamos el modelo para permitir la automatización.
El método de modelado de dos pasos combina las ventajas de usar FEM y la suite computacional neuronal para resolver la ecuación del cable de la neurona en presencia de una estimulación extracelular. Un FEM es útil para calcular con precisión el campo extracelular a través del conductor de volumen, que a menudo no es práctico de resolver analíticamente en el caso de geometría compleja o falta de homogeneidad de conductividad. El costo computacional de este modelo también es relativamente bajo, ya que se asume una condición estática.
Si bien el método de modelado descrito es ventajoso en su facilidad de uso y flexibilidad, existen limitaciones para este flujo de trabajo de modelado. En primer lugar, este método no permitía la presencia de una membrana neural en el cálculo del campo eléctrico. Joucla et al.25 compararon el método de dos pasos con todo el método FEM, donde la geometría neural y las propiedades de la membrana se incluyeron en el modelo FEM. Demostraron que incluir la neurona en el cálculo del campo eléctrico cambiaría el cálculo del potencial transmembrana cuando se incluyera una estructura celular más grande, como un cuerpo celular, en la geometría. Específicamente, la simplificación de la geometría neuronal en el método de dos pasos significa que el potencial transmembrana de cualquier punto en un compartimiento está representado por el potencial transmembrana en el nodo o el punto central del compartimento. En contraste, el modelo FEM completo propuesto por Joucla incluía una representación explícita de la geometría 3D de la neurona, lo que permitió la evaluación individual del potencial transmembrana en cualquier punto dentro del compartimento. Por lo tanto, el modelo FEM completo podría ser más adecuado si se necesita la forma exacta y la ubicación del potencial transmembrana. Sin embargo, este método es computacionalmente más costoso que el método de dos pasos.
La segunda limitación del método de modelado se refiere a la disponibilidad de datos de morfología y cinética iónica. El modelo utilizado aquí se basó en los datos de la salamandra tigre, que se ha utilizado para modelar CGR de otras especies, pero podría haber habido diferencias en los tipos de canales iónicos presentes que no se han dilucidado. Por lo tanto, en algunos casos puede ser necesario realizar trabajos in vitro para ajustar los parámetros del canal iónico.
En tercer lugar, el costo del software FEM podría ser una limitación. En este caso, un programa FEM26 de código abierto que tenga un solucionador de ecuaciones de Poisson incorporado podría ser una alternativa. Además del software FEM utilizado, el software utilizado en este flujo de trabajo es gratuito. Si bien el software FEM utilizado ofrece una GUI intuitiva y un modelado de corriente eléctrica listo para usar, es posible realizar los cálculos de valor extracelular en un software de programación de propósito general. Sin embargo, esto requeriría definir manualmente las ecuaciones físicas y los métodos numéricos para resolver las ecuaciones27. Además, este método puede ser tedioso cuando se va a utilizar una geometría compleja de tejido o matriz de electrodos.
Divulgaciones
Los autores declaran que no hay intereses contrapuestos.
Agradecimientos
Esta investigación está financiada por The National Health and Medical Research Council Project Grant (Número de subvención 1109056).
Materiales
| Name | Company | Catalog Number | Comments |
| Computer workstation | N/A | N/A | Windows 64-bit operating system, at least 4GB of RAM, at least 3 GB of disk space |
| Anaconda Python | Anaconda Inc. | Version 3.9 | The open source Individual Edition containing Python 3.9 and preinstalled packages to perform data manipulation, as well as Spyder Integrated Development Environment. It could be used to control the simulation, as well as to display and analyse the simulation data. |
| COMSOL Multiphysics | COMSOL | Version 5.6 | The simulation suite to perform finite element modelling. The licence for the AC/DC module should be purchased. The Application Builder capability should be included in the licence to follow the automation tutorial. |
| NEURON | NEURON | Version 8.0 | A freely-distributed software to perform the computation of neuronal cells and/or neural networks. |
Referencias
- Greenberg, R. J., Velte, T. J., Humayun, M. S., Scarlatis, G. N., de Juan, E. A computational model of electrical stimulation of the retinal ganglion cell. IEEE Transactions on Bio-medical Engineering. 46 (5), 505-514 (1999).
- Guo, T., et al. Mediating retinal ganglion cell spike rates using high-frequency electrical stimulation. Frontiers in Neuroscience. 13, 413 (2019).
- Loizos, K., et al. Increasing electrical stimulation efficacy in degenerated retina: Stimulus waveform design in a multiscale computational model. IEEE Transactions on Neural Systems and Rehabilitation Engineering. 26 (6), 1111-1120 (2018).
- Cao, X., Sui, X., Lyu, Q., Li, L., Chai, X. Effects of different three-dimensional electrodes on epiretinal electrical stimulation by modeling analysis. Journal of Neuroengineering and Rehabilitation. 12 (1), 73 (2015).
- Wilke, R. G. H., Moghadam, G. K., Lovell, N. H., Suaning, G. J., Dokos, S. Electric crosstalk impairs spatial resolution of multi-electrode arrays in retinal implants. Journal of Neural Engineering. 8 (4), 046016 (2011).
- AC/DC module user's guide. COMSOL AB Available from: https://doc.comsol.com/5.4/doc/com.comsol.help.acdc/ACDCModuleUsersGuide.pdf (2018)
- Malmivuo, P., Malmivuo, J., Plonsey, R. . Bioelectromagnetism: Principles and Applications of Bioelectric and Biomagnetic Fields. , (1995).
- Rall, W. Electrophysiology of a dendritic neuron model. Biophysical Journal. 2, 145-167 (1962).
- Carnevale, N. T., Hines, M. L. . The Neuron Book. , (2006).
- Rattay, F. The basic mechanism for the electrical stimulation of the nervous system. Neuroscience. 89 (2), 335-346 (1999).
- Hodgkin, A. L., Huxley, A. F. A quantitative description of membrane current and its application to conduction and excitation in nerve. The Journal of Physiology. 117 (4), 500-544 (1952).
- Liang, T., et al. Threshold suprachoroidal-transretinal stimulation current required by different-size electrodes in rabbit eyes. Ophthalmic Research. 45 (3), 113-121 (2011).
- Jensen, R. J., Rizzo, J. F., Ziv, O. R., Grumet, A., Wyatt, J. Thresholds for activation of rabbit retinal ganglion cells with an ultrafine, extracellular microelectrode. Investigative Ophthalmology and Visual Science. 44 (8), 3533-3543 (2003).
- Kim, W., Choi, M., Kim, S. -. W. The normative retinal and choroidal thicknesses of the rabbit as revealed by spectral domain optical coherence tomography. Journal of the Korean Ophthalmological Society. 62 (3), 354-361 (2021).
- Guo, T., et al. Influence of cell morphology in a computational model of ON and OFF retinal ganglion cells. 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). 2013, 4553-4556 (2013).
- Haberbosch, L., et al. Safety aspects, tolerability and modeling of retinofugal alternating current stimulation. Frontiers in Neuroscience. 13, 783 (2019).
- Sheasby, B. W., Fohlmeister, J. F. Impulse encoding across the dendritic morphologies of retinal ganglion cells. Journal of Neurophysiology. 81 (4), 1685-1698 (1999).
- Rockhill, R. L., Daly, F. J., MacNeil, M. A., Brown, S. P., Masland, R. H. The diversity of ganglion cells in a mammalian retina. Journal of Neuroscience. 22 (9), 3831-3843 (2002).
- Lukasiewicz, P., Werblin, F. A slowly inactivating potassium current truncates spike activity in ganglion cells of the tiger salamander retina. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience. 8 (12), 4470-4481 (1988).
- Van Rossum, G. . Python Reference Manual. , (1995).
- . Welcome to Spyder's Documentation - Spyder 5 documentation Available from: https://docs.spyder-idle.org/current/index.html (2022)
- Rattay, F. Ways to approximate current-distance relations for electrically stimulated fibers. Journal of Theoretical Biology. 125 (3), 339-349 (1987).
- Tsai, D., Morley, J. W., Suaning, G. J., Lovell, N. H. Direct activation and temporal response properties of rabbit retinal ganglion cells following subretinal stimulation. Journal of Neurophysiology. 102 (5), 2982-2993 (2009).
- Tsai, D., Morley, J. W., Suaning, G. J., Lovell, N. H. Frequency-dependent reduction of voltage-gated sodium current modulates retinal ganglion cell response rate to electrical stimulation. Journal of Neural Engineering. 8 (6), 066007 (2011).
- Joucla, S., Glière, A., Yvert, B. Current approaches to model extracellular electrical neural microstimulation. Frontiers in Computational Neuroscience. 8, 13 (2014).
- . OpenFOAM Available from: https://www.openfoam.com/ (2022)
- Barba, L., Forsyth, G. CFD Python: The 12 steps to Navier-Stokes equations. Journal of Open Source Education. 1 (9), 21 (2018).
Reimpresiones y Permisos
Solicitar permiso para reutilizar el texto o las figuras de este JoVE artículos
Solicitar permisoExplorar más artículos
This article has been published
Video Coming Soon
ISSN 1940-087X
ACERCA DE JoVE
Copyright © 2025 MyJoVE Corporation. Todos los derechos reservados
Utilizamos cookies para mejorar su experiencia en nuestra página web.
Al continuar usando nuestro sitio web o al hacer clic en 'Continuar', está aceptando nuestras cookies.