Method Article
Computational Modeling of Retinal Neurons for Visual Prosthesis Research - Grundlegende Ansätze
In diesem Artikel
Zusammenfassung
Wir fassen einen Workflow zusammen, um das Verhalten eines Netzhautneurons als Reaktion auf elektrische Stimulation rechnerisch zu modellieren. Das Berechnungsmodell ist vielseitig und umfasst Automatisierungsschritte, die nützlich sind, um eine Reihe von physiologischen Szenarien zu simulieren und die Ergebnisse zukünftiger In-vivo/In-vitro-Studien zu antizipieren.
Zusammenfassung
Die computergestützte Modellierung ist aufgrund ihrer Fähigkeit, das Verhalten von In-vivo- und In-vitro-Systemen vorherzusagen, zu einer immer wichtigeren Methode im neuronalen Engineering geworden. Dies hat den entscheidenden Vorteil, dass die Anzahl der in einer bestimmten Studie benötigten Tiere minimiert wird, indem eine oft sehr genaue Vorhersage physiologischer Ergebnisse ermöglicht wird. Auf dem Gebiet der visuellen Prothese hat die computergestützte Modellierung eine Reihe praktischer Anwendungen, einschließlich der Information über das Design eines implantierbaren Elektrodenarrays und die Vorhersage visueller Wahrnehmungen, die durch die Abgabe elektrischer Impulse von diesem Array ausgelöst werden können. Einige in der Literatur beschriebene Modelle kombinieren eine dreidimensionale (3D) Morphologie zur Berechnung des elektrischen Feldes und ein Kabelmodell des interessierenden Neurons oder neuronalen Netzwerks. Um die Zugänglichkeit dieser zweistufigen Methode für Forscher zu erhöhen, die möglicherweise nur begrenzte Erfahrung mit der computergestützten Modellierung haben, stellen wir ein Video der grundlegenden Ansätze zur Verfügung, die zur Konstruktion eines Computermodells zu ergreifen sind, und verwenden es zur Vorhersage der physiologischen und psychophysischen Ergebnisse von Stimulationsprotokollen, die über eine visuelle Prothese. Der Leitfaden umfasst die Schritte zum Erstellen eines 3D-Modells in einer Finite-Elemente-Modellierungssoftware (FEM), die Konstruktion eines retinalen Ganglienzellmodells in einer multikompartimentären Neuronen-Computersoftware, gefolgt von der Verschmelzung der beiden. Eine Finite-Elemente-Modellierungssoftware zur numerischen Lösung physikalischer Gleichungen würde verwendet werden, um die elektrische Feldverteilung in den elektrischen Stimulationen von Gewebe zu lösen. Dann wurde eine spezielle Software verwendet, um die elektrischen Aktivitäten einer neuronalen Zelle oder eines Netzwerks zu simulieren. Um diesem Tutorial zu folgen, wäre die Vertrautheit mit dem Funktionsprinzip einer Neuroprothese sowie neurophysiologischen Konzepten (z. B. Aktionspotentialmechanismus und Verständnis des Hodgkin-Huxley-Modells) erforderlich.
Einleitung
Visuelle Neuroprothesen sind eine Gruppe von Geräten, die Stimulationen (elektrisch, Licht usw.) an die Nervenzellen auf dem Sehweg abgeben, um Phosphene oder das Gefühl des Sehens des Lichts zu erzeugen. Es ist eine Behandlungsstrategie, die seit fast einem Jahrzehnt für Menschen mit dauerhafter Erblindung durch degenerative Netzhauterkrankungen klinisch eingesetzt wird. Typischerweise würde ein komplettes System eine externe Kamera umfassen, die die visuellen Informationen um den Benutzer herum erfasst, ein Netzteil und eine Recheneinheit, um das Bild zu verarbeiten und in eine Reihe von elektrischen Impulsen zu übersetzen, und ein implantiertes Elektrodenarray, das das neuronale Gewebe verbindet und die elektrischen Impulse an die Nervenzellen liefert. Das Funktionsprinzip ermöglicht es, eine visuelle Neuroprothese an verschiedenen Stellen entlang des Sehwegs von der Netzhaut zum visuellen Kortex zu platzieren, solange sie dem geschädigten Gewebe nachgeschaltet ist. Ein Großteil der aktuellen Forschung im Bereich visueller Neuroprothesen konzentriert sich auf die Erhöhung der Wirksamkeit der Stimulation und die Verbesserung der räumlichen Sehschärfe, um ein natürlicheres Sehen zu ermöglichen.
Bei den Bemühungen, die Wirksamkeit der Stimulation zu verbessern, war die computergestützte Modellierung eine kostengünstige und zeiteffiziente Methode, um ein Prothesendesign zu validieren und sein visuelles Ergebnis zu simulieren. Computergestützte Modellierung in diesem Bereich gewann seit 1999 an Popularität, als Greenberg1 die Reaktion einer retinalen Ganglienzelle auf extrazelluläre elektrische Reize modellierte. Seitdem wird die computergestützte Modellierung verwendet, um die Parameter des elektrischen Impulses2,3 oder das geometrische Design der Elektrode 4,5 zu optimieren. Trotz der unterschiedlichen Komplexität und der Forschungsfragen arbeiten diese Modelle, indem sie die elektrische Spannungsverteilung im Medium (z. B. Nervengewebe) bestimmen und die elektrische Reaktion abschätzen, die die Neuronen in der Nähe aufgrund der elektrischen Spannung erzeugen.
Die elektrische Spannungsverteilung in einem Leiter kann durch Lösen der Poisson-Gleichungen6 an allen Stellen ermittelt werden:
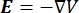
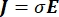
wobei E das elektrische Feld, V das elektrische Potential, J die Stromdichte und σ die elektrische Leitfähigkeit ist. Die  in der Gleichung gibt einen Gradientenoperator an. Bei stationärem Strom werden dem Modell folgende Randbedingungen auferlegt:
in der Gleichung gibt einen Gradientenoperator an. Bei stationärem Strom werden dem Modell folgende Randbedingungen auferlegt:


wobei n die Senkrechte zur Fläche ist, Ω die Grenze darstellt und I0 den spezifischen Strom darstellt. Zusammen erzeugen sie eine elektrische Isolierung an den Außengrenzen und erzeugen eine Stromquelle für eine ausgewählte Grenze. Wenn wir eine monopolare Punktquelle in einem homogenen Medium mit isotroper Leitfähigkeit annehmen, kann das extrazelluläre elektrische Potential an einem beliebigen Ort durch7 berechnet werden:

wobei Ie der Strom und der Abstand zwischen der Elektrode und dem Messpunkt ist. Wenn das Medium inhomogen oder anisotrop ist oder das Elektrodenarray mehrere Elektroden aufweist, kann eine Berechnungssuite zur numerischen Lösung der Gleichungen praktisch sein. Eine Finite-Elemente-Modellierungssoftware6 zerlegt den Volumenleiter in kleine Abschnitte, die als "Elemente" bezeichnet werden. Die Elemente sind miteinander verbunden, so dass die Auswirkungen der Veränderung in einem Element die Veränderung in anderen beeinflussen, und es löst die physikalischen Gleichungen, die zur Beschreibung dieser Elemente dienen. Mit der steigenden Rechengeschwindigkeit moderner Computer kann dieser Prozess innerhalb von Sekunden abgeschlossen werden. Sobald das elektrische Potential berechnet ist, kann man die elektrische Reaktion des Neurons abschätzen.
Ein Neuron sendet und empfängt Informationen in Form von elektrischen Signalen. Solche Signale gibt es in zwei Formen - abgestufte Potentiale und Aktionspotentiale. Abstufte Potentiale sind vorübergehende Änderungen des Membranpotentials, wobei die Spannung über der Membran positiver (Depolarisation) oder negativer (Hyperpolarisation) wird. Abgestufte Potenziale haben typischerweise lokalisierte Effekte. In Zellen, die sie produzieren, sind Aktionspotentiale Alles-oder-Nichts-Reaktionen, die lange Strecken entlang der Länge eines Axons zurücklegen können. Sowohl abgestufte als auch Aktionspotentiale sind empfindlich gegenüber der elektrischen und chemischen Umgebung. Eine Aktionspotentialspitze kann von verschiedenen neuronalen Zelltypen, einschließlich der retinalen Ganglienzellen, erzeugt werden, wenn ein Schwellentransmembranpotential überschritten wird. Das Aktionspotential Spiking und die Ausbreitung lösen dann die synaptische Übertragung von Signalen an nachgeschaltete Neuronen aus. Ein Neuron kann als Kabel modelliert werden, das in zylindrische Segmente unterteilt ist, wobei jedes Segment aufgrund der Lipiddoppelschichtmembran8 Kapazität und Widerstand aufweist. Ein Neuronen-Rechenprogramm9 kann die elektrische Aktivität einer elektrisch erregbaren Zelle abschätzen, indem es die Zelle in mehrere Kompartimente diskretisiert und das mathematische Modell10 löst:
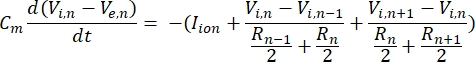
In dieser Gleichung ist Cmdie Membrankapazität, V e,n ist das extrazelluläre Potential am Knoten n, Vi,n das intrazelluläre Potential am Knoten n, R n der intrazelluläre (longitudinale) Widerstand am Knoten n und I-Ion ist der Ionenstrom, der durch die Ionenkanäle am Knoten nfließt. Die Werte von V aus dem FEM-Modell werden als Ve,n für alle Knoten im Neuron implementiert, wenn die Stimulation aktiv ist.
Die Transmembranströme aus Ionenkanälen können unter Verwendung der Hodgkin-Huxley-Formulierungen11 modelliert werden:
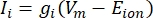
wobei g i die spezifische Leitfähigkeit des Kanals, V m das Transmembranpotential (V i,n - Ve,n) und E Ion das Umkehrpotential des Ionenkanals ist. Für spannungsabhängige Kanäle wie Na-Kanal werden dimensionslose Parameter m und h eingeführt, die die Wahrscheinlichkeit des Öffnens oder Schließens der Kanäle beschreiben:
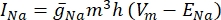
wobei  die maximale Membranleitfähigkeit für den jeweiligen Ionenkanal ist und die Werte der Parameter m und h durch Differentialgleichungen definiert sind:
die maximale Membranleitfähigkeit für den jeweiligen Ionenkanal ist und die Werte der Parameter m und h durch Differentialgleichungen definiert sind:

wobei α x und βx spannungsabhängige Funktionen sind, die die Ratenkonstanten des Ionenkanals definieren. Sie haben im Allgemeinen die Form:

Die Werte der Parameter in diesen Gleichungen, einschließlich der maximalen Leitfähigkeit, sowie die Konstanten A, B, C und D, wurden typischerweise aus empirischen Messungen gefunden.
Mit diesen Bausteinen können Modelle unterschiedlicher Komplexität erstellt werden, indem die beschriebenen Schritte ausgeführt werden. Eine FEM-Software ist nützlich, wenn die Poisson-Gleichung nicht analytisch gelöst werden kann, z. B. bei inhomogener oder anisotroper Leitfähigkeit im Volumenleiter oder wenn die Geometrie des Elektrodenarrays komplex ist. Nachdem die extrazellulären Potentialwerte gelöst wurden, kann das Neuronenkabelmodell in der Neuronen-Rechensoftware numerisch gelöst werden. Die Kombination der beiden Software ermöglicht die Berechnung einer komplexen Neuronenzelle oder eines Netzwerks zu einem ungleichmäßigen elektrischen Feld.
Ein einfaches zweistufiges Modell einer retinalen Ganglienzelle unter suprachoroidaler Stimulation wird mit den oben genannten Programmen erstellt. In dieser Studie wird die retinale Ganglienzelle einer Reihe von Größenordnungen elektrischer Stromimpulse ausgesetzt. Die Position der Zelle relativ zum Reiz wird ebenfalls variiert, um die Distanz-Schwellen-Beziehung zu zeigen. Darüber hinaus umfasst die Studie eine Validierung des Berechnungsergebnisses gegen eine In-vivo-Studie der kortikalen Aktivierungsschwelle unter Verwendung unterschiedlicher Größen der Stimulationselektrode12 sowie eine In-vitro-Studie, die die Beziehung zwischen dem Elektroden-Neuron-Abstand und der Aktivierungsschwelle 13 zeigt.
Protokoll
1. Aufbau des Finite-Elemente-Modells für elektrische Potentialberechnungen
- Ermittlung der Simulationsschritte und der Komplexität des Modells
HINWEIS: Ziel des ersten Schritts ist es, den Zweck der Modellierung zu klären, die die notwendigen Elemente des Modells und des Simulationsverfahrens bestimmt. Ein wichtiger zu berücksichtigender Punkt ist das Verhalten von Nervenzellen, das vom Modell gezeigt werden muss, und welches Testprotokoll erforderlich wäre, um dieses Verhalten zu demonstrieren. Diese Studie zeigt eine Entfernungsschwellenbeziehung für ein Neuron, das extrazellulär stimuliert wird, sowie die Elektrodengrößenschwellenkurve. Um dies zu tun, ist ein neuronales Zellmodell erforderlich, das in verschiedene Abschnitte unterteilt ist (um die Variation morphologischer und biophysikalischer Parameter im Neuron einzubeziehen), die für extrazelluläre Spannungen empfindlich sind, und eine Simulation einer Reihe von Elektrodengrößen und -positionen.- Definieren Sie die Forschungsfrage und die experimentellen Variablen.
- Definieren Sie eine Forschungsfrage und ein Testprotokoll, um die Konstruktion des Modells zu leiten. Es ist am besten, mit einer klaren Frage zu beginnen und ein Modell zu erstellen, das so einfach wie möglich ist, um es zu beantworten.
- Bestimmen Sie die erforderlichen Elemente, die in das vollständige Modell aufgenommen werden sollen
HINWEIS: Bei diesem Modellierungsansatz wird die Zelle als in ein elektrisch leitfähiges Medium, dh das biologische Gewebe, eingetaucht. Die elektrische Stimulation erfolgt über diesen "Volumenleiter", d.h. das Medium, was zu einer Verteilung des elektrischen Potentials führt.- Basierend auf den zu lösenden Forschungsfragen und Variablen entscheiden Sie, ob beide Elemente (FEM- und Neuronenkabelmodell) erforderlich sind. Wenn die Modellierung beispielsweise eine einzelne Elektrode benötigt, die als Punktquelle vereinfacht werden kann und dass das Medium homogen ist, ist ein FEM möglicherweise nicht erforderlich, und eine analytische Berechnung des extrazellulären elektrischen Feldes kann durchgeführt werden, um es zu ersetzen.
- Definieren Sie die Forschungsfrage und die experimentellen Variablen.
- Laden Sie die Software herunter und installieren Sie sie.
HINWEIS: Die Studie verwendete die Versionen von Softwareanwendungen (COMSOL, NYNON und Python Anaconda) und Hardware, die in der Materialtabelle angegeben sind. Es kann geringfügige Unterschiede in den Schritten oder Ergebnissen geben, wenn verschiedene Versionen der Software/Hardware verwendet werden.- Laden Sie die Software herunter, die zum Betriebssystem des Computers passt, und erwerben Sie ggf. eine Lizenz. Stellen Sie sicher, dass alle erforderlichen Simulationsmodule heruntergeladen sind, und installieren Sie die gesamte Software.
- Sammeln Sie die Daten über die Anatomie des zu modellierenden Gewebes und der zu modellierenden Zelle
HINWEIS: Für diese Methode wurden die anatomischen und biophysikalischen Parameter aus empirischen Befunden entnommen. Es ist üblich, dass Computermodelle Parameter mischen, die in verschiedenen Arten gemessen wurden, da keine Daten verfügbar sind. Für eine Simulation der suprachoroidalen Stimulation müssen die Gewebeschichten zwischen der stimulierenden und der Referenzelektrode in das Modell einbezogen werden.- Sammeln Sie die Anatomie des Gewebes aus histologischen Studien.
- In diesem Modell umfassen Sie die Aderhaut, das Netzhautgewebe und die Glaskörperbereiche, wobei jede Domäne als rechteckiges Prisma modelliert ist, um die Konstruktion des Modells zu erleichtern. Sammeln Sie die durchschnittliche Netzhautgewebedicke aus veröffentlichten histologischen Daten14 , um später als Höhe jedes Prismas verwendet zu werden.
- Sammeln Sie die Einzelzellmorphologiedaten aus der Zellfärbung oder der öffentlichen Neuronendatenbank.
- Laden Sie die detaillierte Neuronenmorphologie aus einer Datenbank wie NeuroMorpho.org herunter, die eine Suchmetadatenfunktion bietet, um das relevante Neuron basierend auf Spezies, Gehirnregion, Zelltyp usw. zu finden. Für diese Studie finden Sie Guos OFF RGC-Modell (D23WM13_27_1-OffRGC_msa)15 , indem Sie Kaninchen > Neuseeland Weiß im Feld Spezies und Netzhaut im Feld Gehirnregion eingeben. Klicken Sie auf das Modell und laden Sie die .swc-Datei herunter.
- Sammeln Sie die Anatomie des Gewebes aus histologischen Studien.
- Sammeln Sie die biophysikalischen Daten der modellierten Zelle
HINWEIS: Zu den biophysikalischen Parametern gehören die elektrischen Leitfähigkeitswerte für jede Gewebeschicht und die elektrischen Parameter der Nervenmembran und der Ionenkanäle.- Aufgrund der Verfügbarkeit von Daten sollten die elektrischen Leitfähigkeitswerte, die dem Kaninchen16 entnommen wurden, für das Gewebemodell verwendet werden, während die Dynamik der Ionenkanäle auf dem Sheasby- und Fohlmeister-Modell der Tigersalamander-Netzhaut17 basiert.
- Erstellen Sie die Geometrie des Finite-Elemente-Modells des Gewebes und der Elektrode in der FEM-Software
HINWEIS: Die Geometrie des Gewebes und der Elektrodenanordnung beeinflussen beide die elektrische Potentialverteilung, was wiederum das Verhalten der Nervenzellen beeinflusst. Daher ist es wichtig, eine realistische Geometrie des Mediums aufzubauen, in dem sich die Zellen befinden, sowie der Elektrode. Die in diesem Tutorial verwendete FEM-Software verfügt über eine GUI, die eine einfache Konstruktion der Modellgeometrie ermöglicht.- Einrichten des FEM-Modells in der GUI der Software:
- Führen Sie die FEM-Software aus und klicken Sie auf Modellassistent > 3D. Erweitern Sie im Listenfeld Physik auswählen die AC/DC-> Elektrische Felder und Strom > elektrische Ströme (ec), und klicken Sie dann auf Hinzufügen. Klicken Sie auf Studie, fügen Sie unter der Option Allgemeine Studien eine stationäre Studie hinzu, und klicken Sie dann auf Fertig (ergänzende Abbildung 1).
- Einstellung der Einheit und der geometrischen Parameter der Elektrode.
- Klicken Sie im Modell-Generator-Baum auf Parameter 1. Geben Sie in der Tabelle 'elec_rad' in das Feld Name und '50' in das Feld Ausdruck ein, um eine Elektrode mit einem Radius von 50 Einheiten zu erstellen. Klicken Sie dann auf Geometrie und ändern Sie die Längeneinheit in μm, da das Soma einer typischen retinalen Ganglienzelle einen Durchmesser von etwa 10 μm hat (ergänzende Abbildung 2).
- Erstellen Sie die Gewebeschichten mithilfe von Blockdomänen
HINWEIS: Um die Modellgeometrie zu erstellen, wurden drei Blöcke verwendet, um verschiedene Strukturen im Auge darzustellen. Block 1 repräsentierte die Aderhaut, Block 2 das Netzhautgewebe und Block 3 den Glaskörper.- Klicken Sie mit der rechten Maustaste auf Geometrie 1 > Block, um eine Blockdomäne zu erstellen. Wiederholen Sie diesen Schritt noch zwei weitere Male, um insgesamt drei Blöcke zu erstellen. Stellen Sie für alle Blöcke sowohl die Tiefe als auch die Breite auf 5.000 μm ein und ändern Sie die Option Basis (unter Position) in Zentrieren. Weisen Sie jedem Block die folgenden Werte für Höhe (unter Größe und Form) und z (unter Position) zu:
Block 1: Höhe = 112 μm, z = 0 μm
Block 2: Höhe = 151 μm, z = 131,5 μm
Block 3: Höhe = 5.000 μm, z = 2.707 μm
- Klicken Sie mit der rechten Maustaste auf Geometrie 1 > Block, um eine Blockdomäne zu erstellen. Wiederholen Sie diesen Schritt noch zwei weitere Male, um insgesamt drei Blöcke zu erstellen. Stellen Sie für alle Blöcke sowohl die Tiefe als auch die Breite auf 5.000 μm ein und ändern Sie die Option Basis (unter Position) in Zentrieren. Weisen Sie jedem Block die folgenden Werte für Höhe (unter Größe und Form) und z (unter Position) zu:
- Erstellen einer Arbeitsebene zum Hinzufügen einer Elektrode zum Modell
- Klicken Sie im Modellbaum mit der rechten Maustaste auf Geometrie 1, und wählen Sie Arbeitsebene. Klicken Sie auf Arbeitsebene 1 und ändern Sie den Ebenentyp in Parallel ausgerichtet, klicken Sie auf die Schaltfläche Auswahl aktivieren unter dem Ebenentyp und wählen Sie die Unterseite von Block 1 (blk 1 > 1).
- Zeichnen einer Scheibenelektrode auf der Arbeitsebene
- Klicken Sie unter Arbeitsebene 1 auf Ebenengeometrie und klicken Sie in der Hauptsymbolleiste auf Skizze. Wählen Sie Kreis, klicken Sie auf der Registerkarte Grafiken auf eine beliebige Stelle im Rechteck, und ziehen Sie, um eine Disc-Elektrode zu erstellen. Ändern Sie den Radius auf "elec_rad" μm, xw und yw auf 0 μm und klicken Sie dann auf Alle erstellen.
- Materialeigenschaften jeder Domäne zuordnen
HINWEIS: Wenn Sie die Schritte zum Erstellen der Geometrie ausführen, wird das Modell in mehrere "Domänen" unterteilt, bei denen es sich um einzelne 3D-Teile handelt, aus denen die gesamte Geometrie besteht. Jeder Domäne sollte ein elektrischer Leitfähigkeitswert zugewiesen werden, um die elektrische Feldverteilung im gesamten Modell zu berechnen.- Klicken Sie im Modellbaum mit der rechten Maustaste auf Material > leeres Material, klicken Sie dann auf Material 1 , und ändern Sie die Auswahl in Manuell.
- Klicken Sie im Grafikfenster auf die Domänen, sodass nur Domäne 1 ausgewählt wird. Wählen Sie Materialeigenschaften > Grundlegende Eigenschaften > Elektrische Leitfähigkeit, klicken Sie auf die Schaltfläche Zu Material hinzufügen und ändern Sie den Wert für die elektrische Leitfähigkeit auf 0,043 S / m15.
- Wiederholen Sie die Schritte für die Domänen 2 und 3 mit den elektrischen Leitfähigkeitswerten 0,7 16 bzw. 1,5516 S/m (ergänzende Abbildung 3).
- Vernetzen eines 3D-Modells: Um das Modell zu vernetzen, gehen Sie zum Modellbaum und klicken Sie mit der rechten Maustaste auf Netz 1 > Freie Tetraeder. Klicken Sie auf Free Tetrahedral 1 und wählen Sie Build All.
HINWEIS: Der Vernetzungsprozess zerlegt die gesamte Geometrie in kleinere "Elemente" (ein Element ist ein virtuelles Segment der Modellgeometrie, in dem die physikalischen Gleichungen numerisch gelöst werden). Die Vernetzung mit kleineren Elementen erhöht theoretisch die Genauigkeit der Näherung, ist aber rechnerisch erschöpfend. Eine gängige Praxis besteht darin, das Modell mit spärlichem Netz zu starten und das Ergebnis der Simulation aufzuzeichnen, dann die Simulation jedes Mal kontinuierlich mit kleineren Netzelementen zu wiederholen und die Ergebnisse zu vergleichen. Der Verfeinerungsprozess kann beendet werden, wenn es keinen signifikanten Unterschied zwischen den Berechnungsergebnissen und nachfolgenden Verfeinerungsschritten gibt.- Beurteilung der Netzqualität: Klicken Sie mit der rechten Maustaste auf Netz 1 und wählen Sie Statistik , um das Histogramm der Elementqualität anzuzeigen. Befolgen Sie die folgenden Schritte zur Netzverfeinerung, um die Qualität der Elemente zu verbessern.
HINWEIS: Die Verwendung der Standardvernetzung kann zu vielen minderwertigen Elementen führen, was wiederum zu ungenauen Berechnungen führt. In den meisten Fällen ist ein gewisses Maß an Netzverfeinerung erforderlich. - Verfeinerung des Netzes um den Umfang der Elektrode
HINWEIS: Die Bereiche, in denen es zu abrupten Änderungen des elektrischen Feldes kommen könnte, erfordern typischerweise ein verfeinertes Netz. Hier wurde eine dichtere Vernetzung um den Umfang der Elektrode unter Verwendung der Kantenverteilungsfunktion hinzugefügt.- Löschen Sie zunächst das vorhandene Netz von Free Tetrahedral 1. Klicken Sie dann mit der rechten Maustaste auf Mesh 1 > Distribution, klicken Sie auf Distribution 1, ändern Sie die geometrische Objektebene in Edge und wählen Sie Kanten 19-22 (den Umfang der Scheibenelektrode).
- Legen Sie den Verteilungstyp auf Feste Anzahl von Elementen fest und ändern Sie das Feld Anzahl der Elemente in elec_rad*3/10 , um die Elemente relativ klein zu machen.
- Verfeinerung des Netzes über die Aderhaut und das Netzhautgewebe
- Klicken Sie im Modellbaum mit der rechten Maustaste auf Netz 1 > Swept. Klicken Sie auf Swept 1. Wählen Sie Domains 1 und 2 aus. Klicken Sie dann mit der rechten Maustaste auf Mesh 1 > Free Tetraedral, setzen Sie die geometrische Objektebene auf Remaining und klicken Sie auf Build All. (Optional: Überprüfen Sie das Elementqualitätshistogramm erneut, um sicherzustellen, dass die minderwertigen Elemente proportional reduziert wurden.)
- Beurteilung der Netzqualität: Klicken Sie mit der rechten Maustaste auf Netz 1 und wählen Sie Statistik , um das Histogramm der Elementqualität anzuzeigen. Befolgen Sie die folgenden Schritte zur Netzverfeinerung, um die Qualität der Elemente zu verbessern.
- Einrichten des FEM-Modells in der GUI der Software:
- Anwenden der Physik auf das Finite-Elemente-Modell
HINWEIS: Die "Physik" in der FEM-Software sind Sätze mathematischer Gleichungen und Randbedingungen, die dem Modell zugewiesen werden müssen. Es ist die Berechnung der Lösung des simultanen Gleichungssatzes, die während der Ausführung des Modells durchgeführt wird. Die Wahl der Physik, die auf die Geometrie angewendet werden soll, hängt von dem simulierten physikalischen Phänomen ab. Zum Beispiel beobachtet die elektrische Stromphysik, wie sie in diesem Modell verwendet wird, die elektrische Feldverteilung und vernachlässigt das magnetische (induktive) Phänomen. Andere Physik könnte auf die Geometrie angewendet werden, wenn andere physikalische Probleme (z. B. Temperaturverteilung, mechanische Spannung usw.) gelöst werden sollen.- Auswahl der Physik und Anwendung von Randbedingungen
HINWEIS: Wenn ein Konstantspannungsimpuls angelegt werden soll, sollte die variable Potentialrandbedingung durch eine elektrische Potentialrandbedingung ersetzt werden.- Erweitern Sie Elektrische Ströme 1 im Modellbaum und prüfen Sie, ob Stromerhaltung 1, Elektrische Isolierung 1 und Anfangswerte 1 aufgeführt sind. Klicken Sie dann mit der rechten Maustaste auf die Elektrischen Ströme 1 > Masse (diese weist einer entfernten Ebene 0 V zu und simuliert eine entfernte Referenzelektrode) und wenden Sie diese auf die Oberfläche an, die am weitesten von der Elektrode entfernt ist (Oberfläche 10).
- Klicken Sie anschließend mit der rechten Maustaste auf die Elektrischen Ströme 1 > Gleitpotential (dies simuliert eine Stromquelle mit konstantem Strom), die der Scheibenelektrode (Oberfläche 14) zugewiesen ist, und ändern Sie den Wert I 0 in 1[μA], um einen einheitlichen Strom anzuwenden.
- Ausführen der Simulation mit einem parametrischen Sweep.
HINWEIS: In diesem Schritt wird die Simulation ausgeführt, und es wurde ein parametrisches Sweeping hinzugefügt, bei dem mehrere Simulationen durchgeführt wurden, wobei der Wert eines Parameters in jeder Simulation geändert wurde. Hier wurde der Parameter Elektrodenradius gefegt und die elektrische Potentialverteilung für jede Simulation in der Modelldatei gespeichert. Nach dem Ausführen der Simulation wurde der Ergebniszweig in der Modellstruktur mit einem Multislice-Diagramm mit elektrischem Potential (ec) aufgefüllt.- Klicken Sie im Modellbaum mit der rechten Maustaste auf Studie 1 > Parametrischer Sweep. Klicken Sie auf Parametrischer Sweep, klicken Sie in der Tabelle Studieneinstellung auf Hinzufügen und wählen Sie dann elec_rad für den Parameternamen.
- Geben Sie '50, 150, 350, 500' für die Parameterwertliste und 'μm' für die Parametereinheit ein und klicken Sie auf Berechnen , um die Studie auszuführen (ergänzende Abbildung 4).
- Auswahl der Physik und Anwendung von Randbedingungen

Abbildung 1: Erstellen der Tisssue-Geometrie. Zur Darstellung des Gewebes wurde eine Blockgeometrie in das FEM-Modell eingefügt. Bitte klicken Sie hier, um eine größere Version dieser Abbildung zu sehen.
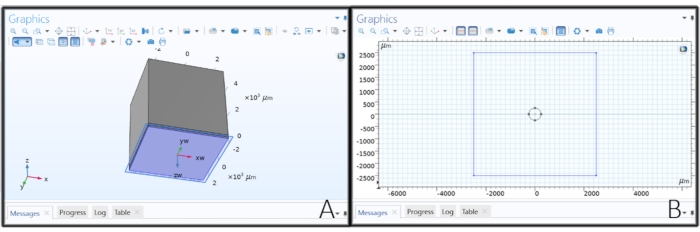
Abbildung 2: Erstellen der Elektrodengeometrie . (A) Erstellen einer Arbeitsebene zum Zeichnen der Scheibenelektrode. (B) Skizzieren eines Kreises auf einer Arbeitsebene, um eine Scheibenelektrode zu erzeugen. Bitte klicken Sie hier, um eine größere Version dieser Abbildung zu sehen.

Abbildung 3: Das Elementqualitätshistogramm des FEM-Modells. Das Histogramm zeigte die Qualität der Elemente im gesamten Modell. Netzverfeinerungen sind erforderlich, wenn sich ein erheblicher Teil der Elemente im minderwertigen Bereich befindet. Bitte klicken Sie hier, um eine größere Version dieser Abbildung zu sehen.
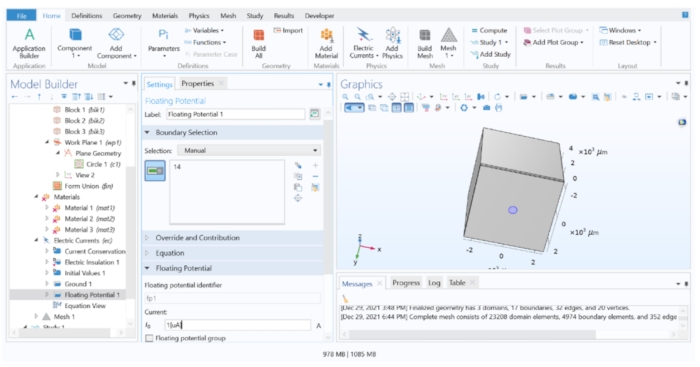
Abbildung 4: Zuweisen eines Stromwerts zur Elektrode. Ein einheitlicher Strom, der in der FEM-Software an die Geometrie der Elektrode angelegt wird. Bitte klicken Sie hier, um eine größere Version dieser Abbildung zu sehen.
2. Importieren der Geometrie der neuronalen Zelle in die GUI der Neuron-Rechensuite
- Erstellen der Geometrie des Zellmodells
- Importieren der Morphologie mit der Cell Builder-Funktion.
- Führen Sie 'nrngui' aus dem Installationsordner der Neuron-Rechensuite aus, klicken Sie auf Extras > Verschiedenes > 3D importieren und aktivieren Sie dann das Kontrollkästchen Datei auswählen .
- Suchen Sie die heruntergeladene .swc-Datei und klicken Sie auf Lesen. Nachdem die Geometrie importiert wurde, klicken Sie auf Export > Cell Builder (Ergänzende Abbildung 5).
- Erstellen einer .hoc-Datei der importierten Zellmorphologie
- Gehen Sie zur Registerkarte Teilmengen und beobachten Sie die Teilmengen , die im Modell vordefiniert wurden (z. B. Soma, Axon, Basal usw.). Aktivieren Sie das Kontrollkästchen Continuous Create , gehen Sie zu Management > Export und exportieren Sie die Morphologie als "rgc.hoc".
- Betrachten der Morphologie der Zelle
- Klicken Sie in der Symbolleiste auf Werkzeug > Modellansicht > 1 Real Cells > Root Soma[0], klicken Sie mit der rechten Maustaste auf das erscheinende Fenster und klicken Sie auf Achsentyp > Ansichtsachse. Bei Sichtprüfung beträgt der dendritische Felddurchmesser dieses Modells rund 250 μm. Schließen Sie vorerst die NEURON-Fenster.
- Importieren der Morphologie mit der Cell Builder-Funktion.

Abbildung 5: Exportieren der Neuronenmodellinformationen als .hoc-Datei. Die Geometrie des Neurons wurde in eine .hoc-Datei exportiert, um weitere Änderungen zu ermöglichen. Bitte klicken Sie hier, um eine größere Version dieser Abbildung zu sehen.
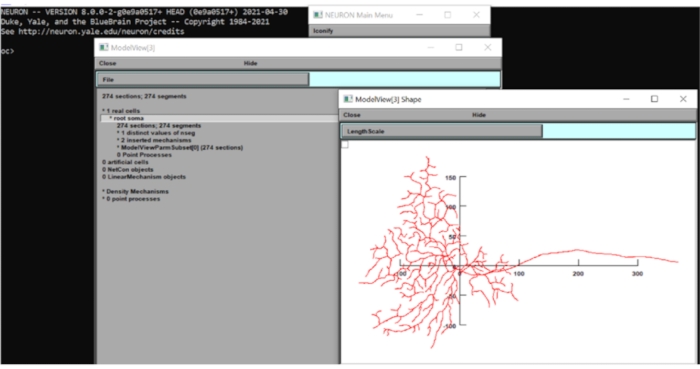
Abbildung 6: Messung der Dimension des Neurons. Die Morphologie des Neurons (Draufsicht) wurde in der GUI der Neuronen-Rechensuite mit überlagerten x-y-Achsen angezeigt. Die Skala war in μm. Bitte klicken Sie hier, um eine größere Version dieser Abbildung zu sehen.
3. Programmierung der NEURON-Rechensimulation
- Anpassung der Zellmorphologie durch Programmierung in .hoc-Sprache
HINWEIS: Die Morphologie der Zelle kann über die Cell Builder-Funktion der GUI angepasst werden. Es wird jedoch gezeigt, wie dies durch Bearbeiten der .hoc-Datei erreicht werden kann, um den Prozess zu beschleunigen. Die .hoc-Datei definiert die Topologie (physikalische Verbindungen zwischen jedem Teil der Neuronen), die Morphologie (die Länge, den Durchmesser und die Lage jedes Neuronenabschnitts) und die biophysikalischen Eigenschaften (Ionenkanalparameter) der modellierten Zelle. Die vollständige Dokumentation zur .hoc-Programmierung finden Sie in: https://neuron.yale.edu/neuron/static/new_doc/index.html#,- Öffnen Sie die resultierende .hoc-Datei mit einem Texteditor (z. B. Editor). Fügen Sie ein Axon-Anfangssegment von 40 μm Länge und ein schmales axonales Segment von 90 μm Länge in der Nähe des Somas hinzu, wie in Sheasby und Fohlmeister17 beschrieben, sowie die Länge der Dendriten so ändern, dass die dendritische Feldgröße 180 μm beträgt, um der G1-Zelle in Rockhill et al.18 zu entsprechen.
- Erstellen neuer Zellschnitte und Definieren der topologischen Verbindungen für jeden Abschnitt.
- Um neue Zellabschnitte für das Axon-Anfangssegment (AIS) und das schmale axonale Segment (NS) zu erstellen, fügen Sie diese Zeilen am Anfang der Datei rgc.hoc hinzu:
AIS, NS erstellen // Deklarieren von Zellkompartimenten namens AIS und NS
Ersetzen Sie dann die Zeile 'connect axon(0), soma[1](1)' durch:
connect ais(0), soma[1](1) // Verbinden des ersten Segments von AIS mit dem Ende von soma[1]
connect ns(0), ais(1) // Verbinden des ersten NS-Segments mit dem Ende von AIS
connect axon(0), ns(1) // Verbinden des ersten Segments des Axons mit dem Ende von NS
- Um neue Zellabschnitte für das Axon-Anfangssegment (AIS) und das schmale axonale Segment (NS) zu erstellen, fügen Sie diese Zeilen am Anfang der Datei rgc.hoc hinzu:
- Definieren der 3D-Positionen, Durchmesser und Länge der Zellschnitte
- Definieren Sie die 3D-Positionen und -Durchmesser der AIS- und NS-Fächer, indem Sie diese Zeilen in die Klammern "proc shape3d_31()" schreiben:
ais { pt3dadd(-2.25, -1.55, 0, 1) // Die ersten drei Zahlen sind die xyz-Koordinate und der Durchmesser beträgt 1 μm
pt3dadd(37.75, -1.55; 0, 1)} // Der erste Punkt liegt bei x = -2,25 μm und der letzte Punkt bei x = 37,75 μm
ns { pt3dadd(37.75, -1.55, 0, 0.3) // Die 3D-Koordinaten und der Durchmesser für die NS-Segmente
pt3dadd(127.75, -1.55, 0, 0.3)} - Verschieben Sie am Ende der Datei die 3D-Koordinate des Axons so, dass der Anfangspunkt mit dem Endpunkt von NS übereinstimmt, indem Sie Folgendes eingeben:
axon {for i=0,n3d()-1 {pt3dchange(i, x3d(i)+130, y3d(i),z3d(i)-5, diam3d(i))}} //Verschieben der x-Koordinate - Kürzen Sie am Ende der Datei die dendritischen Kompartimente um 18%, indem Sie Folgendes eingeben:
forsec basal {L=L*0,82} // Skalierung der Länge, um die dendritische Feldgröße zu verkleinern
define_shape() // Fehlende 3D-Informationen ergänzen
- Definieren Sie die 3D-Positionen und -Durchmesser der AIS- und NS-Fächer, indem Sie diese Zeilen in die Klammern "proc shape3d_31()" schreiben:
- Erstellen neuer Zellschnitte und Definieren der topologischen Verbindungen für jeden Abschnitt.
- Öffnen Sie die resultierende .hoc-Datei mit einem Texteditor (z. B. Editor). Fügen Sie ein Axon-Anfangssegment von 40 μm Länge und ein schmales axonales Segment von 90 μm Länge in der Nähe des Somas hinzu, wie in Sheasby und Fohlmeister17 beschrieben, sowie die Länge der Dendriten so ändern, dass die dendritische Feldgröße 180 μm beträgt, um der G1-Zelle in Rockhill et al.18 zu entsprechen.
- Definieren der Anzahl der Segmente für jeden Abschnitt
HINWEIS: Jeder Abschnitt des Neurons kann räumlich diskretisiert werden, ähnlich wie der Prozess der Vernetzung im FEM-Modell. Die räumliche Diskretisierung unterteilt das Neuron virtuell in kleinere Segmente, in denen Berechnungen durchgeführt werden sollen. Stellen Sie für die Anzahl der Segmente 'nseg' sicher, dass ungerade Zahlen verwendet werden, um sicherzustellen, dass sich am Mittelpunkt eines Zellabschnitts ein interner Knoten befindet, und versuchen Sie, die nseg-Zahl zu verdreifachen, bis die Berechnung ein konsistentes Ergebnis9 ergibt. Eine höhere Anzahl von Segmenten führt zu einer genaueren numerischen Näherung, erhöht aber auch die Rechenlast.- Um den Diskretisierungsprozess zu veranschaulichen, fügen Sie die folgenden Zeilen in der Datei rgc.hoc hinzu, um die neuronalen Abschnitte in den somatischen und axonalen Teilmengen in mehrere Segmente zu unterteilen:
forsec somatisch {nseg=31}
forsec axonal {nseg=301}
Andere Abschnitte im Modell müssen ebenfalls diskretisiert werden, indem diese Zeilen eingegeben werden, aber der Name der Teilmenge (nach 'forsec') und die Anzahl der Segmente (nach 'nseg') wie gewünscht geändert werden.
- Um den Diskretisierungsprozess zu veranschaulichen, fügen Sie die folgenden Zeilen in der Datei rgc.hoc hinzu, um die neuronalen Abschnitte in den somatischen und axonalen Teilmengen in mehrere Segmente zu unterteilen:
- Fügen Sie benutzerdefinierte Ionenkanalmechanismen ein
- Schreiben von benutzerdefinierten Ionenkanalmechanismen als .mod-Dateien: Um die Ionenkanalmechanismen anzuwenden, erstellen Sie .mod-Dateien und fügen Sie die Dateien in den biophysikalischen Abschnittsteil der .hoc-Datei ein, indem Sie die Schritte 3.3.1-3.3.3 ausführen. Die .mod-Datei enthält die Variablen und die zu lösenden Differentialgleichungen für jeden Ionenkanal.
HINWEIS: Korrekte Definitionen und Implementierungen von Ionenkanalmechanismen sind in genauen Neuronensimulationen von entscheidender Bedeutung. Überprüfen Sie beim Schreiben von .mod-Dateien, ob die Einheiten korrekt sind (das bereitgestellte Dienstprogramm "modlunit", das ausgeführt werden kann, um die Konsistenz der Einheiten zu überprüfen) und ob die Gleichungen korrekt geschrieben sind. Um zu testen, dass die Ionenkanalmechanismen korrekt sind, kann der Strom für jeden Ionenkanal während der intrazellulären oder extrazellulären Stimulation aufgetragen und mit empirischen Befunden verglichen werden.- Spannungsgesteuerte Ionenkanäle
HINWEIS: Eine .mod-Datei zum Erstellen eines spannungsabhängigen Ionenkanals enthält typischerweise einen DERIVATIVE-Block , der die zu lösende Differentialgleichung enthält, einen BREAKPOINT-Block mit den Befehlen zum Lösen der Differentialgleichungen mit einer ausgewählten numerischen Näherungsmethode und PROCEDURE-Blöcke , die das Programm anweisen, die Gating-Parameter zu berechnen (z. B. mt, ht und d in diesem Beispiel). Dieser Code berechnet die Werte des Ionenstroms, der für jeden Zeitschritt durch den Kanal fließt.- Um den Prozess zu veranschaulichen, erstellen Sie einen spannungsabhängigen Ca-Kanal, der Differentialgleichungen erster Ordnung für die Gating-Variablen löst.
- Öffnen Sie eine neue Datei im Texteditor und geben Sie die Zeilen in das Feld Ergänzungsmaterial definieren eines spannungsabhängigen Cat-Kanals ein. Speichern Sie diese Datei als Cat.mod im selben Ordner wie die .hoc-Datei. Dieser Vorgang muss für die anderen Ionenkanäle, die das Modellneuron enthält, wiederholt werden.
- Spannungs- und konzentrationsabhängige Ionenkanäle
- Die Kinetik einiger Ionenkanäle, wie der Calcium-aktivierten Kaliumkanäle in den retinalen Ganglienzellen, hängt neben der Transmembranspannung auch von der intrazellulären Kalziumkonzentration ab19. Um diesen Mechanismustyp zu modellieren, erstellen Sie eine Datei mit dem Namen KCa.mod, und geben Sie die Linien ein, wie unter Zusätzliche materialspannungs- und konzentrationsabhängige Ionenkanäle gezeigt. In dieser .mod-Datei wurde die Variable 'cai' berechnet, die als interne Konzentration von Ca-Ionen definiert ist, und dann wird diese Variable in der Gleichung verwendet, um den iKCa-Strom zu berechnen.
- Spannungsgesteuerte Ionenkanäle
- Kompilieren von .mod-Dateien
- Kompilieren Sie alle .mod-Dateien, indem Sie das Dienstprogramm mknrndll der Neuron-Computersuite aus dem Installationsordner ausführen. Suchen Sie den Ordner, in dem sich die .mod-Dateien befinden, und klicken Sie auf Kompilieren, um O- und C-Dateien zu erstellen. Danach können die Mechanismen in dieses Zellmodell eingefügt werden.
- Anwendung der .mod-Dateien in der Haupt-NEURON-Modelldatei.
HINWEIS: Neben dem Einfügen der Ionenkanäle wurde die maximale Na-Leitfähigkeit nur für die "somatische" Teilmenge definiert. Bei Bedarf konnten wir die maximale Membranleitfähigkeit für verschiedene neuronale Segmente individuell anpassen.- Aus Gründen der Kürze kombinieren Sie alle Ionenkanalmechanismen in einer einzigen .mod-Datei (Supplementary Material-Complete .mod file). Fügen Sie die kombinierte .mod-Datei, die alle Ionenkanäle und einen passiven Leckkanal enthält, zu allen Segmenten in der Teilmenge "somatisch" ein, indem Sie die folgenden Zeilen in die Prozedur "biophys" der Datei rgc.hoc eingeben:
forsec somatic {insert rgcSpike
PAS einfügen // passiver Leckkanal
gnabar_rgcSpike = 80e-3
g_pas = 0,008e-3 // Leitwert der Leckmembran}
- Aus Gründen der Kürze kombinieren Sie alle Ionenkanalmechanismen in einer einzigen .mod-Datei (Supplementary Material-Complete .mod file). Fügen Sie die kombinierte .mod-Datei, die alle Ionenkanäle und einen passiven Leckkanal enthält, zu allen Segmenten in der Teilmenge "somatisch" ein, indem Sie die folgenden Zeilen in die Prozedur "biophys" der Datei rgc.hoc eingeben:
- Einstellung des axoplasmatischen Widerstands
- Die Zellen haben einen axoplasmatischen Widerstand, der pro Kompartiment verändert werden kann. Bei diesem Modell haben alle Segmente den gleichen spezifischen Widerstand von 110 Ω·cm. Ändern Sie den axoplasmatischen Widerstand in der Datei rgc.hoc:
forall {Ra = 110}
- Die Zellen haben einen axoplasmatischen Widerstand, der pro Kompartiment verändert werden kann. Bei diesem Modell haben alle Segmente den gleichen spezifischen Widerstand von 110 Ω·cm. Ändern Sie den axoplasmatischen Widerstand in der Datei rgc.hoc:
- Schreiben von benutzerdefinierten Ionenkanalmechanismen als .mod-Dateien: Um die Ionenkanalmechanismen anzuwenden, erstellen Sie .mod-Dateien und fügen Sie die Dateien in den biophysikalischen Abschnittsteil der .hoc-Datei ein, indem Sie die Schritte 3.3.1-3.3.3 ausführen. Die .mod-Datei enthält die Variablen und die zu lösenden Differentialgleichungen für jeden Ionenkanal.
- Extrazelluläre Mechanismen einfügen und Pulswellenform definieren
- Einfügen eines extrazellulären Mechanismus in das Zellmodell
- Damit das Zellmodell auf extrazelluläre Spannung reagiert, fügen Sie einen extrazellulären Mechanismus in alle Segmente ein, indem Sie die Zeile am Ende der Datei rgc.hoc eingeben:
forall {extrazellulär} einfügen
- Damit das Zellmodell auf extrazelluläre Spannung reagiert, fügen Sie einen extrazellulären Mechanismus in alle Segmente ein, indem Sie die Zeile am Ende der Datei rgc.hoc eingeben:
- Erstellen eines biphasischen Impulses
HINWEIS: In dieser Demonstration wird ein biphasischer Konstantstromimpuls erstellt, der in Bezug auf Pulsbreite, Interphasenabstand und Anzahl der Wiederholungen durch Erstellen einer Prozedur in einer HOC-Datei vom Benutzer einstellbar ist. Für ein strukturierteres Programm verwenden Sie die Datei rgc.hoc als Datei, um das Zellmodell zu erstellen, während der Stimulationsprozess in einer separaten .hoc-Datei angewendet wird, die das Zellmodell lädt, auf das die Stimulation angewendet wird.- Erstellen Sie eine neue Textdatei mit dem Namen stimulation.hoc, und starten Sie den Code, indem Sie die Zellenmodelldatei laden. Erstellen Sie dann einen biphasischen Puls, indem Sie ein Verfahren definieren, wie in Ergänzendes Material - Erstellen eines biphasischen Pulses in der Neuronensimulation gezeigt.
HINWEIS: Dieser Schritt erzeugt einen kathodischen biphasischen Konstantstromimpuls, bei dem die Stimulusparameter vom Benutzer beim Ausführen der Simulation angegeben werden müssen. Derzeit beträgt die Größe der anodischen und kathodischen Pulse ±1 μA, aber diese Größe muss sich in Abhängigkeit vom Stimulationsstrom ändern, der von der Scheibenelektrode abgegeben wird.
- Erstellen Sie eine neue Textdatei mit dem Namen stimulation.hoc, und starten Sie den Code, indem Sie die Zellenmodelldatei laden. Erstellen Sie dann einen biphasischen Puls, indem Sie ein Verfahren definieren, wie in Ergänzendes Material - Erstellen eines biphasischen Pulses in der Neuronensimulation gezeigt.
- Einfügen eines extrazellulären Mechanismus in das Zellmodell
4. Ausführen und Automatisieren mehrerer Simulationen
- Kombinieren der Modelle
- Extrahieren der Koordinaten für die Knoten im Neuronenzellmodell
HINWEIS: Der Zweck der Kombination der Simulationen besteht darin, die extrazellulären Potenzialwerte zu erfassen, die jedem Knoten des Zellmodells entsprechen. Die Koordinaten der beiden Modelle müssen jedoch aufeinander abgestimmt sein. In diesem Beispiel wurde das mittlere Segment des Somas (Soma(0,5)) so ausgerichtet, dass es auf der horizontalen Mittelebene des Netzhautgewebes (entsprechend der retinalen Ganglienzellschicht) liegt, wobei sich der mittlere Knoten des Somas direkt über dem Zentrum der Scheibenelektrode befindet.- Öffnen Sie das FEM-Modell und notieren Sie sich die Koordinate eines Referenzpunkts (z. B. die horizontale Mittelebene des Netzhautgewebes über der Mitte der Scheibenelektrode), in diesem Fall ist sie [0, 0, 131,5] μm.
- Erstellen Sie in der Neuronen-Berechnungssuite eine Datei namens calculateCoord.hoc, um die Koordinaten des Schwerpunkts jedes Segments zu extrahieren und jeden Abschnitt so zu verschieben, dass das mittlere Segment des Somas dieselbe Koordinate wie der Referenzpunkt im FEM-Modell hat (Supplementary Material-Calculation the coordinate of each node).
- Speichern der Koordinatenpunkte in einer Textdatei
- Führen Sie die Datei calculateCoord.hoc aus (entweder durch Doppelklick aus dem Datei-Explorer oder durch Öffnen der GUI der Neuronen-Rechensuite; klicken Sie dann auf Datei > laden hoc in der Symbolleiste). Speichern Sie die Koordinaten für die auszuwertenden extrazellulären Spannungswerte in einer Textdatei mit dem Namen 'coordinates.dat'.
- Ausführen der Simulationen und Speichern der Spannungsdaten in einer Textdatei
HINWEIS: In diesem Schritt haben wir die berechneten extrazellulären Werte aus dem FEM-Modell extrahiert, aber wir würden nur die Daten von den relevanten Koordinaten speichern, die mit dem Zentrum jedes Zellsegments übereinstimmen. Folgen Sie Schritt 4.1.6.2, wenn eine große Anzahl von Potenzialen zum Exportieren erforderlich ist.- Öffnen Sie die Gewebemodelldatei in der FEM-Software; Wechseln Sie in der Modellhierarchie zur Überschrift Ergebnisse, und klicken Sie auf > Daten > Daten exportieren 1. Stellen Sie sicher, dass das Dataset auf Studie 1/Parametrische Lösungen 1 festgelegt ist, und geben Sie dann "V" in die Spalte Ausdruck und "mV" in die Spalte Einheit ein.
- Ändern Sie unter Ausgabe den Dateinamen in extrazellulär.dat, und wählen Sie Punkte aus, die ausgewertet werden sollen in: Aus Datei. Laden Sie die Koordinaten.dat für das Feld Koordinatendatei , und klicken Sie dann auf Exportieren.
- Anwendung des biphasischen Pulses auf das Zellmodell
HINWEIS: In diesem Stadium sind die extrazellulären Spannungswerte für jedes Zellsegment zu einem Zeitpunkt (wobei der Strom 1 μA beträgt) verfügbar. Da die Studie beabsichtigt, die Zelle einem biphasischen Impuls auszusetzen, wird der extrazelluläre Spannungswert, den die Zelle erfährt, mit der Zeit mit der "vector.play" -Methode ändern.- Fügen Sie die Linien hinzu, die in der Ergänzungsmaterial-Anwendung des biphasischen Pulses in der Stimulation.hoc gezeigt sind.
- Ausführen der kombinierten Simulation
HINWEIS: Ein Zeitintervall 'dt' für die numerischen Näherungen muss definiert werden, um die Simulationen auszuführen. Ähnlich wie nseg kann ein kürzeres dt die Rechengenauigkeit erhöhen, aber auch die Rechenkosten erhöhen.- Fügen Sie die in der Simulation Ergänzendes Material-Ausführen der Neuronen gezeigten Zeilen am Ende der Stimulation.hoc hinzu. Doppelklicken Sie dann auf die Datei stimulation.hoc, um das Skript zu laden und die Simulation automatisch auszuführen. Das Transmembranpotential des interessierenden Segments kann in der GUI der Neuronen-Rechensuite angezeigt werden (Schritt 4.2.1) oder in einer Textdatei gespeichert werden, um in anderen Programmen gelesen zu werden (Schritt 4.1.6.1.2). Führen Sie die Schritte 4.1.6.1 und 4.1.6.2 aus, wenn wiederholte Berechnungen und eine große Anzahl von Membranpotentialen exportiert werden müssen.
- Extra: Automatisierung von Simulationen
HINWEIS: Um eine Schwellenamplitude zu finden, wiederholen Sie die Simulation mehrmals mit jeweils einer anderen Stromamplitude. Eine weitere Automatisierung könnte erforderlich sein, um die Schwelle für Neuronen zu finden, die sich an verschiedenen Positionen relativ zur stimulierenden Elektrode befinden. Ein Automatisierungsschritt kann in der Neuronen-Rechensuite mit einer Prozedur sowie in der FEM-Software mit einem Skript namens "Methode" durchgeführt werden.- Automatisierung der Neuronensimulation zur Ermittlung einer Schwellenamplitude
HINWEIS: Eine Reihe von Neuronensimulationen kann automatisch durchgeführt werden. Die folgenden Schritte werden im Neuronensimulationsprogramm implementiert, um die Schwellenamplituden von Neuronen unter verschiedenen Stimulationsparametern zu finden.- Erstellen Sie eine Prozedur zum Wiederholen der Simulation im Neuronensimulationsprogramm: Erstellen Sie in stimulation.hoc einen Vektor, der einen Bereich der zu testenden Stromamplitude enthält. Erstellen Sie dann eine Prozedur zum Anwenden der Stromamplitude und zeichnen Sie das Vorhandensein einer Spitze auf (eine positive Änderung von einer negativen zu einer positiven Transmembranspannung), und die Schwellenamplitude wird als die niedrigste Stromamplitude definiert, die eine Spitze verursacht. Definieren Sie dazu am Ende der Datei stimulation.hoc eine Prozedur namens findTh() (Supplementary Material-Looping over a range of current amplitudes)
- Speichern der Antwort am Schwellenwert in einer Textdatei: Fügen Sie die folgenden Zeilen zur findTh()-Prozedur in stimulation.hoc hinzu, um die berechneten Transmembranspannungswerte für alle Neuronenkompartimente aus jedem Zeitschritt in einer Textdatei zu speichern:
sprint(saveFileName, "Response_%d.dat", th) // Schwellenwert speichern
saveFile.wopen(saveFileName)
for i=0,(responseVector.size()-1){
saveFile.printf("%g, ", responseVector.x[i])
if(i==responseVector.size()-1) {saveFile.printf("%g\n", responseVector.x[i])
saveFile.close(saveFileName)
}}
- Automatisierung in der FEM-Software, um die Spannungswerte für Neuronen an verschiedenen Orten zu finden
HINWEIS: Eine weitere Automatisierung, die durchgeführt werden kann, ist die automatische Erfassung von extrazellulären Spannungswerten für Neuronen an verschiedenen Orten. Das Application Builder-Menü in der FEM-Software bietet die Möglichkeit, eine "Methode" oder ein Skript zu definieren, um die Schritte zu automatisieren, die die Software zur Durchführung von Berechnungen benötigt. Zur Demonstration wird die Position der Zelle in x-Richtung in einem 100-μm-Schritt um das 5-fache verschoben (ergänzende Abbildung 6).- Schreiben eines Codes für die Automatisierung von FEM-Simulationen.
- Gehen Sie zum Application Builder, klicken Sie mit der rechten Maustaste auf Methoden im Application Builder-Baum, wählen Sie Neue Methode und klicken Sie auf OK. Gehen Sie zu Datei- > Einstellungen > Methoden, aktivieren Sie das Kontrollkästchen Alle Codes anzeigen und klicken Sie auf OK.
- Schreiben Sie ein .hoc-Skript, das die Koordinatendatei lädt, verschieben Sie die Werte an die gewünschte Position und speichern Sie eine Textdatei mit den Spannungswerten für die neue Position der Zelle, indem Sie die Codes eingeben, die im Abschnitt Ergänzendes Material - Definieren einer Methode zur Automatisierung von FEM-Simulationen angezeigt werden.
- Ausführen der automatisierten Schritte in der FEM-Software: Wechseln Sie zur Methode Model Builder, Developer > Run > Methode 1. Dadurch werden .dat Dateien mit den entsprechenden Spannungswerten erzeugt, die als extracellular_1.dat, extracellular_2.dat usw. bezeichnet werden.
- Schreiben eines Codes für die Automatisierung von FEM-Simulationen.
- Schleifen der Simulationen in einer Allzweck-Programmiersprache
HINWEIS: Um die Simulationen in einer Schleife zu wiederholen, muss jedes Mal die entsprechende Textdatei in die Simulation der Neuronen-Berechnungssuite geladen werden, und eine Programmiersprache20 , die Textdateien einfach laden und bearbeiten kann, ist praktisch, um diesen Schritt auszuführen. Für diesen Schritt kann jede beliebige integrierte Entwicklungsumgebung (IDE)21 verwendet werden.- Öffnen Sie die ausgewählte IDE, klicken Sie auf Neue Datei , um ein neues Skript zu erstellen. Hier wird in diesem Beispiel eine .py Datei verwendet. Geben Sie die Zeilen ein, die unter Ergänzendes Material – Ausführen der Simulationen in einer allgemeinen Programmiersprache angezeigt werden.
- Klicken Sie abschließend auf Ausführen oder drücken Sie F5 , um das Skript auszuführen, wodurch auch die GUI geöffnet wird (ergänzende Abbildung 7).
- Automatisierung der Neuronensimulation zur Ermittlung einer Schwellenamplitude
- Extrahieren der Koordinaten für die Knoten im Neuronenzellmodell
- Anzeige von Simulationsdaten
HINWEIS: Wenn Sie alle oben genannten Schritte ausführen, sollten die Simulationsergebnisse in Textdateien gespeichert werden, die den Schwellenwert und das Transmembranpotential am Schwellenwert enthalten. Der Benutzer hat jedoch die Möglichkeit, das Simulationsergebnis anzuzeigen, während die Simulation über die GUI von NEURON ausgeführt wird.- Grafische Darstellung der Reaktion des Neuronenmodells auf die extrazelluläre Stimulation in der GUI der Neuronen-Rechensuite. Führen Sie dazu stimulation.hoc aus, klicken Sie in der Symbolleiste auf Diagramm > Spannungsachse , klicken Sie im Diagrammfenster mit der rechten Maustaste auf eine beliebige Stelle und wählen Sie Plot What.
- Geben Sie 'axon.v(1)' in das Feld Variable to Graph ein, was bedeutet, dass das Transmembranpotential des letzten Segments des Axons pro Zeitschritt dargestellt wird.
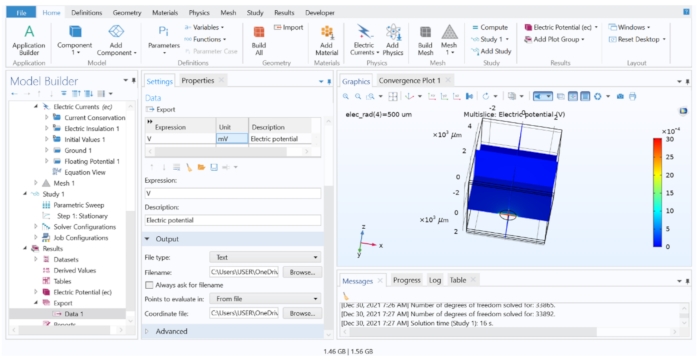
Abbildung 7: Anzeige und Export der FEM-Berechnungsergebnisse in eine Textdatei. Das Grafikfenster mit einem Multislice-Diagramm des elektrischen Potentials in V. Die Optionen in der Datenexporteinstellung ermöglichten den Export der berechneten Variablen in eine Textdatei. Bitte klicken Sie hier, um eine größere Version dieser Abbildung zu sehen.
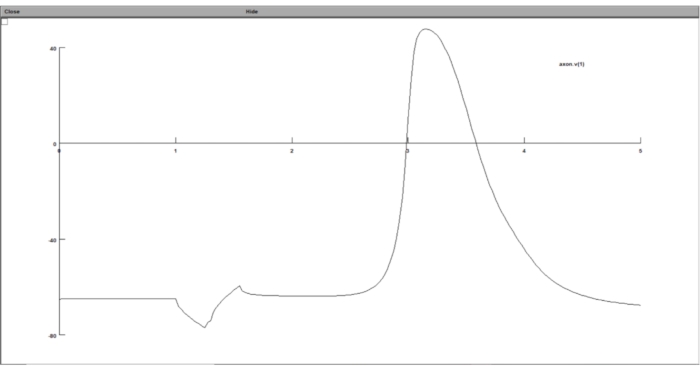
Abbildung 8: Darstellung des Diagramms des Transmembranpotentials unter Verwendung eines Spannungsgraphen. Das Neuronen-Transmembranpotential wurde in der GUI der Neuronen-Rechensuite angezeigt. Die x-Achse ist die Zeit in ms, während die y-Achse das Transmembranpotential des gewählten Neuronensegments in mV ist. Bitte klicken Sie hier, um eine größere Version dieser Abbildung zu sehen.
Ergebnisse
Wir führten zwei Simulationsprotokolle durch, um die Verwendung des Modells zu demonstrieren. Das erste Protokoll beinhaltete die Variation der Elektrodengröße, während die Position des Neurons und die elektrischen Pulsparameter gleich blieben. Das zweite Protokoll bestand darin, das Neuron in 100-μm-Schritten in x-Richtung zu verschieben, während die Größe der Elektrode konstant blieb. Für beide Protokolle war der verwendete Impuls ein einzelner kathodischer biphasischer Impuls von 0,25 ms Breite mit einem Interphasenspalt von 0,05 ms. Für das erste Protokoll wurde der Radius der Elektrode auf 50, 150, 350 und 500 μm variiert, während für das zweite Protokoll der Radius der Elektrode konstant bei 50 μm gehalten wurde.
Das hier beschriebene Modell zeigte, dass eine Erhöhung der suprachoroidalen Elektrodengröße bei 0,25 ms Pulsbreite die Aktivierungsschwelle des Modellneurons erhöhte (Abbildung 9A). Dieses Ergebnis spiegelte die in vivo Ergebnisse von Liang et al.12 wider, die zeigten, dass die kortikale Aktivierungsschwelle mit zunehmender Elektrodengröße bei dieser Pulsbreite zunimmt.
Die Größenordnungen der Aktivierungsschwellen des Modells weichen aufgrund mehrerer Faktoren von den empirischen Befunden ab. Erstens umfasst dieses Modell nur einen einzigen RGC eines bestimmten Typs, der möglicherweise nicht in der Gruppe von Zellen vorhanden ist, die in der In-vivo-Studie aktiviert werden. Als nächstes enthielt dieses Modell kein Netzhautnetzwerk, das die Aktivierung von RGCs durch exzitatorische Inputs von den bipolaren Zellen erleichtern könnte. Ein weiterer möglicher Grund für die Diskrepanz ist der Elektroden-Netzhaut-Abstand. Es ist möglich, dass der Elektroden-Netzhaut-Abstand in der In-vivo-Studie aufgrund anatomischer Variabilität oder der Operation geringer war als in diesem Modell. Folglich haben wir den Elektroden-Netzhaut-Abstand und damit die Aktivierungsschwelle überschätzt. Es ist auch wichtig zu beachten, dass, obwohl dies in unseren Ergebnissen nicht nachgewiesen wurde, die Modellierung einer Einzelzellschwelle die in vivo kortikale Schwelle oft unterschätzen würde. Dies liegt an den technischen Einschränkungen kortikaler Messungen (vor allem in Bezug auf das Signal-Rausch-Verhältnis), dass die kortikale Aktivität typischerweise erst nach Aktivierung mehrerer retinaler Ganglienzellen nachgewiesen wird. Infolgedessen ist eine Diskrepanz in der Größenordnung der retinalen und kortikalen Aktivierungsschwellen zu erwarten. Trotz dieser Unterschiede zeigte dieses Modell erfolgreich den steigenden Trend der Aktivierungsschwelle aufgrund der Zunahme der Elektrodengröße. Dies resultierte aus dem Fehlen eines Bereichs mit hohem elektrischem Feld im Vergleich zu seiner Umgebung, wenn die Elektrodengröße erhöht wird, was die neuronale Aktivierung nicht begünstigte22.
Als nächstes beobachteten wir die Aktionspotentialmerkmale, um das hier beschriebene Modell zu validieren. Die Latenz oder die Zeit zwischen dem Beginn des Stimulus und dem Höhepunkt der Aktionspotentialspitze lag zwischen 1 und 2,2 ms (Abbildung 9B). Dies entsprach der kurzen Latenzspitze aufgrund der nicht netzwerkvermittelten Netzhautaktivierung23. Die Spike-Breite dieses Modells betrug 1 ms und liegt damit im gleichen Bereich wie die Spike-Breiten von Kaninchen-RGCs, die in vitro24 gemessen wurden.
Im zweiten Stimulationsprotokoll wurde nur die Position des Neurons in der x-Achse (entlang der Länge des Axons) relativ zur Elektrode variiert. In einem Abstand von 0 befand sich der Schwerpunkt des Soma-Abschnitts unmittelbar über dem Zentrum der Scheibenelektrode. Negativer Abstand bedeutet, dass die Scheibenelektrode näher an der axonalen Seite positioniert wurde, während positiver Abstand bedeutet, dass die Scheibenelektrode näher an der dendritischen Seite positioniert wurde. Das Modell zeigte, dass die niedrigste Schwelle erreicht wurde, wenn sich das schmale Segment des Axons unmittelbar über der Scheibenelektrode befand, und sie nahm zu, wenn der x-Abstand größer wurde (Abbildung 9C). Das Bewegen der Elektrode weiter in Richtung des distalen Axons erzeugte eine niedrigere Schwelle im Vergleich zum Bewegen der Elektrode in Richtung der Dendriten aufgrund des Vorhandenseins des Axon-Anfangssegments und des schmalen Segments, in dem die Natriumkanäle häufiger vorkommen. Dieses Ergebnis stimmte mit dem In-vitro-Befund von Jensen et al.13 überein, bei dem Kaninchen-RGCs mit einer ultrafeinen Mikroelektrode stimuliert wurden und die Aktivierungsschwelle am höchsten war, wenn die Elektrode näher an die Dendriten verschoben wurde.

Abbildung 9: Die Ergebnisse der Modellierungsmethode . (A) Die Aktivierungsschwellen für eine retinale Ganglienzelle oberhalb der Scheibenelektrode. Der Elektrodenradius wurde variiert (50, 150, 350 und 500 μm) und die Schwelle mit zunehmender Elektrodengröße erhöht. (B) Die Aktionspotentialform des Neuronenmodells bei 0,25 ms Pulsbreite. Die Aktionspotentiale am Schwellenwert für verschiedene Elektrodengrößen haben die gleiche Spikebreite von 1 ms, aber die Latenz nahm mit zunehmender Elektrodengröße zu. Die Stimulus-Anfangszeit betrug 1 ms und die kathodische Phase verursachte eine Depolarisation an der Membran, aber nicht genug, um ein Aktionspotential zu verursachen. (C) Das Neuron wurde entlang der x-Achse verschoben und die Aktivierungsschwellen zeigten, dass die niedrigste Schwelle von dem Neuron erreicht wurde, dessen Soma sich direkt über der Mitte der Elektrode befand. Der Radius der Elektrode betrug 50 μm. Bitte klicken Sie hier, um eine größere Version dieser Abbildung zu sehen.
Ergänzende Abbildung 1: Initialisierung des Finite-Elemente-Modells. Die Arten von Studium und Physik bestimmen die Liste der im Modell gelösten Gleichungen. Diese wurden bei der erstmaligen Erstellung der FEM-Modelldatei festgelegt, können aber auch nach der Erstellung des Modells geändert/hinzugefügt werden. Bitte klicken Sie hier, um diese Datei herunterzuladen.
Ergänzende Abbildung 2: Ändern der Längeneinheit. Die Längeneinheit und die Winkeleinheit bestimmen die Einheiten, die im Geometriedefinitionsprozess verwendet werden. Bitte klicken Sie hier, um diese Datei herunterzuladen.
Ergänzende Abbildung 3: Einfügen einer Materialeigenschaft. Die Materialeigenschaften wurden für jede Domäne in einem 3D-Modell definiert. Die verfügbaren Materialeigenschaften wurden im Fenster Materialeinstellung unter Materialeigenschaften aufgelistet. Für die Berechnung des elektrischen Potentials wurde nur die Eigenschaft Elektrische Leitfähigkeit definiert. Bitte klicken Sie hier, um diese Datei herunterzuladen.
Ergänzende Abbildung 4: Erstellen einer parametrischen Studie zum Durchlaufen einer Liste von Parameterwerten. Eine parametrische Studie ermöglichte es der FEM-Software, die Berechnungen automatisch zu wiederholen und den Elektrodenradiuswert für jede Wiederholung zu ändern. Die Berechnungsergebnisse wurden für jede Wiederholung gespeichert. Bitte klicken Sie hier, um diese Datei herunterzuladen.
Ergänzende Abbildung 5: Importieren der Neuronenmorphologie aus der SWC-Datei. Die Neuronen-Rechensuite war in der Lage, SWC-Dateien zu lesen, die aus der neuronalen Verfolgung gewonnen wurden. Die importierte Datei enthält Informationen über die Morphologie und Topologie jedes Neuronensegments. Bitte klicken Sie hier, um diese Datei herunterzuladen.
Ergänzende Abbildung 6: Automatisierung von FEM-Operationen durch Definition einer Methode. Eine Methode wurde definiert, indem ein Skript geschrieben wurde, um Prozesse in der FEM-Software zu automatisieren, die durch die Definition einer parametrischen Studie nicht möglich sind. Bitte klicken Sie hier, um diese Datei herunterzuladen.
Ergänzende Abbildung 7: Integration der Modelle und Automatisierung der Simulationen mit einer Allzweck-Programmiersprache. Die allgemeine Programmiersprache wurde verwendet, um die Neuronensimulationen zu schleifen, während die extrazelluläre Spannungsdatei als Eingang und die neuronale Antwortspannungsdatei als Ausgabe für jeden Schritt in der Schleife geändert wurden. Bitte klicken Sie hier, um diese Datei herunterzuladen.
Ergänzendes Material: Kommandozeilen für (1) Definition eines spannungsabhängigen Cat-Kanals. (2) Spannungs- und konzentrationsabhängige Ionenkanäle. (3) Vervollständigen Sie die .mod-Datei. (4) Erzeugung eines biphasischen Pulses in der Neuronensimulation. (5) Berechnung der Koordinate jedes Knotens. (6) Anwendung des biphasischen Pulses. (7) Ausführen der Neuronensimulation. (8) Schleife über einen Bereich von Stromamplituden. (9) Definition einer Methode zur Automatisierung von FEM-Simulationen. (10) Ausführung der Simulationen in einer allgemeinen Programmiersprache. Bitte klicken Sie hier, um diese Datei herunterzuladen.
Diskussion
In diesem Artikel haben wir einen Modellierungsworkflow demonstriert, der Finite-Elemente- und biophysikalische Neuronenmodellierung kombiniert. Das Modell ist sehr flexibel, da es in seiner Komplexität an verschiedene Zwecke angepasst werden kann und eine Möglichkeit bietet, die Ergebnisse anhand empirischer Befunde zu validieren. Wir haben auch gezeigt, wie wir das Modell parametrisiert haben, um eine Automatisierung zu ermöglichen.
Die zweistufige Modellierungsmethode kombiniert die Vorteile der Verwendung von FEM und Neuronen-Rechensuite, um die Kabelgleichung des Neurons in Gegenwart einer extrazellulären Stimulation zu lösen. Ein FEM ist nützlich, um das extrazelluläre Feld über den Volumenleiter genau zu berechnen, was im Falle einer komplexen Geometrie oder Inhomogenität der Leitfähigkeit oft nicht analytisch zu lösen ist. Der Rechenaufwand dieses Modells ist ebenfalls relativ gering, da von einem statischen Zustand ausgegangen wird.
Während die beschriebene Modellierungsmethode in ihrer Benutzerfreundlichkeit und Flexibilität vorteilhaft ist, gibt es Einschränkungen für diesen Modellierungsworkflow. Erstens erlaubte diese Methode nicht das Vorhandensein einer neuronalen Membran bei der Berechnung des elektrischen Feldes. Joucla et al.25 verglichen die zweistufige Methode mit der gesamten FEM-Methode, bei der die neuronale Geometrie und die Membraneigenschaften in das FEM-Modell einbezogen wurden. Sie zeigten, dass die Einbeziehung des Neurons in die elektrische Feldberechnung die Transmembranpotentialberechnung verändern würde, wenn eine größere Zellstruktur, wie ein Zellkörper, in die Geometrie einbezogen würde. Insbesondere bedeutet die Vereinfachung der Neuronengeometrie in der zweistufigen Methode, dass das Transmembranpotential eines beliebigen Punktes in einem Kompartiment durch das Transmembranpotential am Knoten oder Mittelpunkt des Kompartiments dargestellt wird. Im Gegensatz dazu enthielt das von Joucla vorgeschlagene Whole-FEM-Modell eine explizite Darstellung der 3D-Geometrie des Neurons, die die individuelle Bewertung des Transmembranpotentials an jedem Punkt innerhalb des Kompartiments ermöglichte. Daher könnte das gesamte FEM-Modell besser geeignet sein, wenn die genaue Form und Position des Transmembranpotentials benötigt wird. Diese Methode ist jedoch rechenintensiver als die zweistufige Methode.
Die zweite Einschränkung der Modellierungsmethode betrifft die Verfügbarkeit von Morphologie- und Ionskinetikdaten. Das hier verwendete Modell basierte auf den Tigersalamanderdaten, die zur Modellierung von RGCs von anderen Arten verwendet wurden, aber es könnte Unterschiede in den vorhandenen Arten von Ionenkanälen gegeben haben, die nicht aufgeklärt wurden. Daher kann es in einigen Fällen notwendig sein, In-vitro-Arbeiten durchzuführen, um die Ionenkanalparameter anzupassen.
Drittens könnten die Kosten der FEM-Software eine Einschränkung darstellen. In diesem Fall könnte ein Open-Source-FEM-Programm26 mit einem eingebauten Poisson-Gleichungslöser eine Alternative sein. Abgesehen von der verwendeten FEM-Software ist die in diesem Workflow verwendete Software kostenlos. Während die verwendete FEM-Software eine intuitive GUI und eine gebrauchsfertige elektrische Strommodellierung bietet, ist es möglich, die extrazellulären Wertberechnungen in einer Allzweck-Programmiersoftware durchzuführen. Dies würde jedoch eine manuelle Definition der physikalischen Gleichungen und der numerischen Methoden zur Lösung der Gleichungen27 erfordern. Darüber hinaus kann diese Methode mühsam sein, wenn eine komplexe Gewebe- oder Elektrodenarray-Geometrie verwendet werden soll.
Offenlegungen
Die Autoren erklären keine Interessenkonflikte.
Danksagungen
Diese Forschung wird durch den National Health and Medical Research Council Project Grant (Grant Number 1109056) finanziert.
Materialien
| Name | Company | Catalog Number | Comments |
| Computer workstation | N/A | N/A | Windows 64-bit operating system, at least 4GB of RAM, at least 3 GB of disk space |
| Anaconda Python | Anaconda Inc. | Version 3.9 | The open source Individual Edition containing Python 3.9 and preinstalled packages to perform data manipulation, as well as Spyder Integrated Development Environment. It could be used to control the simulation, as well as to display and analyse the simulation data. |
| COMSOL Multiphysics | COMSOL | Version 5.6 | The simulation suite to perform finite element modelling. The licence for the AC/DC module should be purchased. The Application Builder capability should be included in the licence to follow the automation tutorial. |
| NEURON | NEURON | Version 8.0 | A freely-distributed software to perform the computation of neuronal cells and/or neural networks. |
Referenzen
- Greenberg, R. J., Velte, T. J., Humayun, M. S., Scarlatis, G. N., de Juan, E. A computational model of electrical stimulation of the retinal ganglion cell. IEEE Transactions on Bio-medical Engineering. 46 (5), 505-514 (1999).
- Guo, T., et al. Mediating retinal ganglion cell spike rates using high-frequency electrical stimulation. Frontiers in Neuroscience. 13, 413 (2019).
- Loizos, K., et al. Increasing electrical stimulation efficacy in degenerated retina: Stimulus waveform design in a multiscale computational model. IEEE Transactions on Neural Systems and Rehabilitation Engineering. 26 (6), 1111-1120 (2018).
- Cao, X., Sui, X., Lyu, Q., Li, L., Chai, X. Effects of different three-dimensional electrodes on epiretinal electrical stimulation by modeling analysis. Journal of Neuroengineering and Rehabilitation. 12 (1), 73 (2015).
- Wilke, R. G. H., Moghadam, G. K., Lovell, N. H., Suaning, G. J., Dokos, S. Electric crosstalk impairs spatial resolution of multi-electrode arrays in retinal implants. Journal of Neural Engineering. 8 (4), 046016 (2011).
- AC/DC module user's guide. COMSOL AB Available from: https://doc.comsol.com/5.4/doc/com.comsol.help.acdc/ACDCModuleUsersGuide.pdf (2018)
- Malmivuo, P., Malmivuo, J., Plonsey, R. . Bioelectromagnetism: Principles and Applications of Bioelectric and Biomagnetic Fields. , (1995).
- Rall, W. Electrophysiology of a dendritic neuron model. Biophysical Journal. 2, 145-167 (1962).
- Carnevale, N. T., Hines, M. L. . The Neuron Book. , (2006).
- Rattay, F. The basic mechanism for the electrical stimulation of the nervous system. Neuroscience. 89 (2), 335-346 (1999).
- Hodgkin, A. L., Huxley, A. F. A quantitative description of membrane current and its application to conduction and excitation in nerve. The Journal of Physiology. 117 (4), 500-544 (1952).
- Liang, T., et al. Threshold suprachoroidal-transretinal stimulation current required by different-size electrodes in rabbit eyes. Ophthalmic Research. 45 (3), 113-121 (2011).
- Jensen, R. J., Rizzo, J. F., Ziv, O. R., Grumet, A., Wyatt, J. Thresholds for activation of rabbit retinal ganglion cells with an ultrafine, extracellular microelectrode. Investigative Ophthalmology and Visual Science. 44 (8), 3533-3543 (2003).
- Kim, W., Choi, M., Kim, S. -. W. The normative retinal and choroidal thicknesses of the rabbit as revealed by spectral domain optical coherence tomography. Journal of the Korean Ophthalmological Society. 62 (3), 354-361 (2021).
- Guo, T., et al. Influence of cell morphology in a computational model of ON and OFF retinal ganglion cells. 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). 2013, 4553-4556 (2013).
- Haberbosch, L., et al. Safety aspects, tolerability and modeling of retinofugal alternating current stimulation. Frontiers in Neuroscience. 13, 783 (2019).
- Sheasby, B. W., Fohlmeister, J. F. Impulse encoding across the dendritic morphologies of retinal ganglion cells. Journal of Neurophysiology. 81 (4), 1685-1698 (1999).
- Rockhill, R. L., Daly, F. J., MacNeil, M. A., Brown, S. P., Masland, R. H. The diversity of ganglion cells in a mammalian retina. Journal of Neuroscience. 22 (9), 3831-3843 (2002).
- Lukasiewicz, P., Werblin, F. A slowly inactivating potassium current truncates spike activity in ganglion cells of the tiger salamander retina. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience. 8 (12), 4470-4481 (1988).
- Van Rossum, G. . Python Reference Manual. , (1995).
- . Welcome to Spyder's Documentation - Spyder 5 documentation Available from: https://docs.spyder-idle.org/current/index.html (2022)
- Rattay, F. Ways to approximate current-distance relations for electrically stimulated fibers. Journal of Theoretical Biology. 125 (3), 339-349 (1987).
- Tsai, D., Morley, J. W., Suaning, G. J., Lovell, N. H. Direct activation and temporal response properties of rabbit retinal ganglion cells following subretinal stimulation. Journal of Neurophysiology. 102 (5), 2982-2993 (2009).
- Tsai, D., Morley, J. W., Suaning, G. J., Lovell, N. H. Frequency-dependent reduction of voltage-gated sodium current modulates retinal ganglion cell response rate to electrical stimulation. Journal of Neural Engineering. 8 (6), 066007 (2011).
- Joucla, S., Glière, A., Yvert, B. Current approaches to model extracellular electrical neural microstimulation. Frontiers in Computational Neuroscience. 8, 13 (2014).
- . OpenFOAM Available from: https://www.openfoam.com/ (2022)
- Barba, L., Forsyth, G. CFD Python: The 12 steps to Navier-Stokes equations. Journal of Open Source Education. 1 (9), 21 (2018).
Nachdrucke und Genehmigungen
Genehmigung beantragen, um den Text oder die Abbildungen dieses JoVE-Artikels zu verwenden
Genehmigung beantragenWeitere Artikel entdecken
This article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten