Method Article
מידול חישובי של נוירוני רשתית לחקר תותבות חזותיות - גישות בסיסיות
In This Article
Summary
אנו מסכמים זרימת עבודה כדי ליצור מודלים חישוביים של התנהגויות של נוירון רשתית בתגובה לגירוי חשמלי. המודל החישובי הוא רב-תכליתי וכולל שלבי אוטומציה שימושיים בהדמיית מגוון תרחישים פיזיולוגיים ובחיזוי התוצאות של מחקרי in vivo/in vitro עתידיים.
Abstract
מודלים חישוביים הפכו לשיטה חשובה יותר ויותר בהנדסה עצבית בשל יכולתה לחזות התנהגויות של מערכות in vivo ו - in vitro . יש לכך יתרון מרכזי של מזעור מספר בעלי החיים הנדרש במחקר נתון על ידי מתן ניבוי מדויק מאוד של תוצאות פיזיולוגיות. בתחום התותבות החזותיות, למודלים חישוביים יש מגוון יישומים מעשיים, כולל יידוע על תכנון מערך אלקטרודות מושתל וחיזוי תפיסות חזותיות שניתן ליצור באמצעות העברת דחפים חשמליים מהמערך האמור. חלק מהמודלים המתוארים בספרות משלבים מורפולוגיה תלת-ממדית (3D) כדי לחשב את השדה החשמלי ומודל כבלים של הנוירון או הרשת העצבית המעניינת. כדי להגביר את הנגישות של שיטה דו-שלבית זו לחוקרים בעלי ניסיון קודם מוגבל במידול חישובי, אנו מספקים סרטון של הגישות הבסיסיות שיש לנקוט על מנת לבנות מודל חישובי ולהשתמש בו לניבוי התוצאות הפיזיולוגיות והפסיכופיזיות של פרוטוקולי גירוי שנפרסו באמצעות תותבת חזותית. המדריך כולל את השלבים לבניית מודל תלת-ממדי בתוכנת מידול אלמנטים סופיים (FEM), בניית מודל תאי גנגליון ברשתית בתוכנה חישובית רב-תאית של נוירונים, ולאחר מכן מיזוג של השניים. תוכנת מידול אלמנטים סופיים לפתרון מספרי של משוואות פיזיקליות תשמש לפתרון חלוקת שדה חשמלי בגירויים החשמליים של רקמות. לאחר מכן, נעשה שימוש בתוכנה מיוחדת להדמיית הפעילות החשמלית של תא עצבי או רשת. כדי לעקוב אחר מדריך זה, תידרש היכרות עם עקרון העבודה של נוירופרוסטזה, כמו גם מושגים נוירופיזיולוגיים (למשל, מנגנון פוטנציאל פעולה והבנה של מודל הודג'קין-האקסלי).
Introduction
נוירו-פרוטזות חזותיות הן קבוצה של מכשירים המספקים גירויים (חשמליים, אור וכו ') לתאים העצביים במסלול הראייה כדי ליצור פוספנים או תחושה של ראיית האור. זוהי אסטרטגיית טיפול שנמצאת בשימוש קליני כבר כמעט עשור עבור אנשים עם עיוורון קבוע הנגרם על ידי מחלות רשתית ניווניות. בדרך כלל, מערכת שלמה תכלול מצלמה חיצונית הלוכדת את המידע החזותי סביב המשתמש, ספק כוח ויחידת מחשוב לעיבוד ותרגום התמונה לסדרה של פולסים חשמליים, ומערך אלקטרודות מושתל המממשק את הרקמה העצבית ומעביר את הפולסים החשמליים לתאים העצביים. עקרון העבודה מאפשר למקם נוירופרוסטזה חזותית באתרים שונים לאורך מסלול הראייה מהרשתית לקליפת המוח הראייתית, כל עוד היא נמצאת במורד הזרם מהרקמה הפגועה. רוב המחקרים הנוכחיים בנוירו-פרוסטזות חזותיות מתמקדים בהגברת היעילות של הגירוי ושיפור החדות המרחבית כדי לספק ראייה טבעית יותר.
במאמצים לשפר את יעילות הגירוי, מידול חישובי היה שיטה חסכונית וחסכונית בזמן כדי לאמת תכנון תותבת ולדמות את התוצאה החזותית שלה. מודלים חישוביים בתחום זה צברו פופולריות מאז 1999 כאשר גרינברג1 מודל את התגובה של תא גנגליון רשתית לגירויים חשמליים חוץ-תאיים. מאז, מודלים חישוביים שימשו כדי לייעל את הפרמטרים של הפולס החשמלי 2,3 או את העיצוב הגיאומטרי של האלקטרודה 4,5. למרות השונות במורכבות ובשאלות המחקר, מודלים אלה פועלים על ידי קביעת חלוקת המתח החשמלי בתווך (למשל, רקמה עצבית) והערכת התגובה החשמלית שהנוירונים בסביבה ייצרו עקב המתח החשמלי.
ניתן למצוא את חלוקת המתח החשמלי במוליך על ידי פתרון משוואות פואסון6 בכל המקומות:
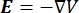
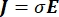
כאשר E הוא השדה החשמלי, V הוא הפוטנציאל החשמלי, J צפיפות הזרם, ו- σ היא המוליכות החשמלית. במשוואה  מציין אופרטור הדרגתי. במקרה של זרם נייח, תנאי הגבול הבאים מוטלים על המודל:
מציין אופרטור הדרגתי. במקרה של זרם נייח, תנאי הגבול הבאים מוטלים על המודל:


כאשר n הוא הנורמלי לפני השטח, Ω מייצג את הגבול, ו-I0 מייצג את הזרם הספציפי. יחד, הם יוצרים בידוד חשמלי בגבולות החיצוניים ויוצרים מקור זרם לגבול שנבחר. אם נניח מקור נקודה מונופולרית בתווך הומוגני בעל מוליכות איזוטרופית, ניתן לחשב את הפוטנציאל החשמלי החוץ-תאי במיקום שרירותי על ידי7:

כאשר Ie הוא הזרם ו- הוא המרחק בין האלקטרודה לנקודת המדידה. כאשר התווך אינו הומוגני או אניזוטרופי, או שלמערך האלקטרודות יש אלקטרודות מרובות, חבילה חישובית לפתרון מספרי של המשוואות יכולה להיות נוחה. תוכנת מידול אלמנטים סופיים6 מפרקת את מוליך הנפח למקטעים קטנים המכונים 'אלמנטים'. האלמנטים קשורים זה בזה כך שהשפעות השינוי באלמנט אחד משפיעות על השינוי באחרים, והוא פותר את המשוואות הפיזיקליות המשמשות לתיאור אלמנטים אלה. עם המהירות החישובית הגוברת של מחשבים מודרניים, תהליך זה יכול להסתיים תוך שניות. לאחר חישוב הפוטנציאל החשמלי, ניתן להעריך את התגובה החשמלית של תא העצב.
נוירון שולח ומקבל מידע בצורה של אותות חשמליים. אותות כאלה מגיעים בשתי צורות - פוטנציאלים מדורגים ופוטנציאלי פעולה. פוטנציאלים מדורגים הם שינויים זמניים בפוטנציאל הממברנה שבהם המתח על פני הממברנה הופך חיובי יותר (דה-פולריזציה) או שלילי יותר (היפרפולריזציה). לפוטנציאלים מדורגים יש בדרך כלל השפעות מקומיות. בתאים שמייצרים אותם, פוטנציאל פעולה הוא תגובות של הכל או לא כלום שיכולות לנוע למרחקים ארוכים לאורך האקסון. הן פוטנציאל מדורג והן פוטנציאל פעולה רגישים לסביבה החשמלית כמו גם הכימית. ספייק פוטנציאלי פעולה יכול להיווצר על ידי סוגי תאים עצביים שונים, כולל תאי גנגליון הרשתית, כאשר פוטנציאל טרנס-ממברנה סף נחצה. פוטנציאל הפעולה מזנק ומתפשט ואז מפעילים העברה סינפטית של אותות לנוירונים במורד הזרם. ניתן לעצב נוירון ככבל המחולק למקטעים גליליים, כאשר לכל מקטע יש קיבוליות והתנגדות עקב הממברנה הדו-שכבתית השומנית8. תוכנית חישובית נוירונים9 יכולה להעריך את הפעילות החשמלית של תא מעורר חשמלית על ידי הפרדת התא למספר תאים ופתרון המודל המתמטי10:
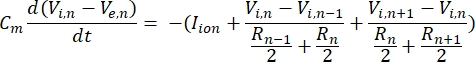
במשוואה זו, Cmהוא קיבוליות הממברנה, V e,n הוא הפוטנציאל החוץ-תאי בצומת n, Vi,n הפוטנציאל התוך-תאי בצומת n, R n ההתנגדות התוך-תאית (אורכית) בצומת n, ויון I הוא הזרם היוני העובר דרך תעלות היונים בצומת n. הערכים של V ממודל FEM מיושמים כ- Ve,n עבור כל הצמתים בנוירון כאשר הגירוי פעיל.
ניתן למדל את הזרמים הטרנס-ממברניים מתעלות יונים באמצעות נוסחאות הודג'קין-האקסלי11:
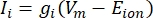
כאשר g i הוא המוליכות הספציפית של התעלה, V m פוטנציאל הטרנסממברנה (V i,n - Ve,n) ויון E פוטנציאל ההיפוך של תעלת היונים. עבור ערוצים מגודרים במתח, כגון ערוץ Na, מוצגים פרמטרים חסרי ממדים, m ו- h, המתארים את ההסתברות לפתיחה או לסגירה של הערוצים:
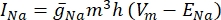
כאשר  היא מוליכות הממברנה המקסימלית עבור תעלת היונים המסוימת, וערכי הפרמטרים m ו-h מוגדרים על ידי משוואות דיפרנציאליות:
היא מוליכות הממברנה המקסימלית עבור תעלת היונים המסוימת, וערכי הפרמטרים m ו-h מוגדרים על ידי משוואות דיפרנציאליות:

כאשר α x ו- βx הן פונקציות תלויות מתח המגדירות את קבועי הקצב של תעלת היונים. הם בדרך כלל לובשים את הטופס:

הערכים של הפרמטרים במשוואות אלה, כולל מוליכות מקסימלית, כמו גם הקבועים A, B, C ו- D, נמצאו בדרך כלל ממדידות אמפיריות.
בעזרת אבני בניין אלה, ניתן לבנות מודלים בעלי מורכבויות שונות על ידי ביצוע השלבים המתוארים. תוכנת FEM שימושית כאשר לא ניתן לפתור את משוואת פואסון באופן אנליטי, כגון במקרה של מוליכות אי-הומוגנית או אניזוטרופית במוליך הנפח או כאשר הגאומטריה של מערך האלקטרודות מורכבת. לאחר שערכי הפוטנציאל החוץ-תאי נפתרו, ניתן לפתור את מודל כבל הנוירונים באופן מספרי בתוכנה החישובית של תא העצב. שילוב שתי התוכנות מאפשר חישוב של תא עצב מורכב או רשת לשדה חשמלי לא אחיד.
מודל דו-שלבי פשוט של תא גנגליון ברשתית תחת גירוי על-טבעי ייבנה באמצעות התוכניות הנ"ל. במחקר זה, תא הגנגליון ברשתית יהיה נתון לטווח של סדרי גודל של פולסים של זרם חשמלי. גם מיקום התא ביחס לגירוי משתנה כדי להראות את הקשר בין סף המרחק. יתר על כן, המחקר כולל אימות של התוצאה החישובית כנגד מחקר in vivo של סף ההפעלה בקליפת המוח תוך שימוש בגדלים שונים של אלקטרודת גירוי12, וכן מחקר במבחנה המראה את הקשר בין מרחק האלקטרודה-נוירון לבין סף ההפעלה13.
Protocol
1. הגדרת מודל האלמנטים הסופיים לחישובי פוטנציאל חשמלי
- קביעת שלבי הסימולציה ומורכבות המודל
הערה: מטרת הצעד הראשון היא להבהיר את מטרת המידול, אשר תקבע את המרכיבים הדרושים של המודל ואת הליך הסימולציה. נקודה חשובה שיש לקחת בחשבון היא ההתנהגות של תאים עצביים שצריכה להיות מוצגת על ידי המודל, ואיזה פרוטוקול בדיקה יידרש כדי להדגים התנהגות זו. מחקר זה מראה קשר מרחק-סף עבור תא עצב המגורה באופן חוץ-תאי, כמו גם את עקומת סף גודל האלקטרודה. לשם כך יש צורך במודל תא עצבי ממודר למקטעים שונים (כדי לשלב את השונות של פרמטרים מורפולוגיים וביופיזיים בנוירון) הרגישים למתח חוץ-תאי ויש צורך בסימולציה של מגוון גדלים ומיקומים של אלקטרודות.- הגדר את שאלת המחקר ואת משתני הניסוי.
- הגדר שאלת מחקר ופרוטוקול בדיקה שינחו את בניית המודל. עדיף להתחיל עם שאלה ברורה ולבנות מודל פשוט ככל האפשר כדי לענות על זה.
- קבע את האלמנטים הדרושים להיכלל במודל השלם
הערה: בגישת מידול זו, התא נתפס כשקוע בתווך מוליך חשמלי, כלומר ברקמה הביולוגית. הגירוי החשמלי מתרחש על פני 'מוליך נפח' זה, כלומר התווך, וכתוצאה מכך התפלגות הפוטנציאל החשמלי.- בהתבסס על שאלות המחקר והמשתנים שיש לפתור, החלט אם שני האלמנטים (FEM ומודל כבל נוירון) נדרשים. אם, למשל, המידול זקוק לאלקטרודה אחת שניתן לפשט כמקור נקודתי ושהתווך הומוגני, ייתכן שלא יהיה צורך ב-FEM, וניתן לבצע חישוב אנליטי של השדה החשמלי החוץ-תאי כדי להחליף אותו.
- הגדר את שאלת המחקר ואת משתני הניסוי.
- הורד והתקן את התוכנה
הערה: המחקר השתמש בגרסאות של יישומי תוכנה (COMSOL, NEURON ו- Python Anaconda) ובחומרה שצוינו בטבלת החומרים. ייתכנו הבדלים קלים בשלבים או בתוצאות אם נעשה שימוש בגרסאות שונות של התוכנה/חומרה.- הורד את התוכנה המתאימה למערכת ההפעלה של המחשב ורכוש רישיון, במידת הצורך. ודא שכל מודולי הסימולציה הנדרשים יורדו והתקינו את כל התוכנות.
- אסוף את הנתונים על האנטומיה של הרקמה והתא כדי להיות מודל
הערה: עבור שיטה זו, הפרמטרים האנטומיים והביופיזיים נלקחו מממצאים אמפיריים. מקובל שמודלים חישוביים מערבבים פרמטרים שנמדדו במינים שונים בשל חוסר הזמינות של נתונים. עבור סימולציה של גירוי על-טבעי, שכבות הרקמה בין אלקטרודות הגירוי והייחוס צריכות להיכלל במודל.- לאסוף את האנטומיה של הרקמה ממחקרים היסטולוגיים.
- במודל זה, כלול את הכורואיד, רקמת הרשתית ותחומי הזגוגית, כאשר כל תחום מעוצב כמנסרה מלבנית לבנייה קלה של המודל. אסוף את עובי רקמת הרשתית הממוצע מנתונים היסטולוגיים שפורסמו14 כדי לשמש מאוחר יותר כגובה של כל מנסרה.
- אסוף את נתוני המורפולוגיה של התא הבודד מתוך צביעת תאים או מסד נתונים ציבורי של נוירונים.
- הורד את המורפולוגיה המפורטת של הנוירונים ממסד נתונים כגון NeuroMorpho.org, המספק תכונת חיפוש מטא-נתונים כדי למצוא את הנוירון הרלוונטי בהתבסס על מינים, אזור במוח, סוג תא וכו '. עבור מחקר זה, מצא את מודל OFF RGC של גואו (D23WM13_27_1-OffRGC_msa)15 על ידי הזנת ארנב > ניו זילנד לבן בשדה מינים ורשתית בשדה אזור המוח . לחץ על המודל והורד את קובץ ה- .swc.
- לאסוף את האנטומיה של הרקמה ממחקרים היסטולוגיים.
- לאסוף את הנתונים הביופיזיקליים של התא במודל
הערה: הפרמטרים הביופיזיקליים כוללים את ערכי המוליכות החשמלית עבור כל שכבת רקמה ואת הפרמטרים החשמליים של הממברנה העצבית ותעלות היונים.- בשל זמינות הנתונים, השתמש בערכי המוליכות החשמלית שנלקחו מהארנב16 עבור מודל הרקמה, בעוד שהדינמיקה של תעלות היונים התבססה על מודל שאסבי ופולמייסטר של רשתית הסלמנדרה הנמר17.
- בניית הגיאומטריה של מודל האלמנט הסופי של הרקמה והאלקטרודה בתוכנת FEM
הערה: הגיאומטריה של הרקמה ומערך האלקטרודות משפיעים שניהם על חלוקת הפוטנציאל החשמלי, אשר בתורו משפיע על התנהגות התא העצבי. לפיכך, בניית גיאומטריה מציאותית של התווך שבו שוכנים התאים, כמו גם האלקטרודה, חשובה. תוכנת FEM המשמשת במדריך זה כוללת ממשק משתמש גרפי המאפשר בנייה קלה של גיאומטריית המודל.- הגדרת מודל FEM בממשק המשתמש הגרפי (GUI) של התוכנה:
- הפעל את תוכנת FEM ולחץ על אשף המודל > תלת מימד. בתיבת הרשימה בחירת פיזיקה, הרחב את AC/DC > שדות חשמליים וזרם > זרמים חשמליים (ec) ולאחר מכן לחץ על הוסף. לחץ על מחקר והוסף מחקר נייח תחת האפשרות לימודים כלליים, ולאחר מכן לחץ על בוצע (איור משלים 1).
- הגדרת היחידה והפרמטרים הגיאומטריים של האלקטרודה.
- בעץ בונה המודלים, לחץ על פרמטרים 1. בטבלה, הקלד 'elec_rad' בשדה Name ו- '50' בשדה 'ביטוי' כדי ליצור אלקטרודה ברדיוס של 50 יחידות. לאחר מכן, לחצו על גיאומטריה, ושנו את יחידת האורך ל-μm, שכן הסומה של תא גנגליון רשתית טיפוסי היא בקוטר של כ-10 מיקרומטר (איור משלים 2).
- יצירת שכבות הרקמה באמצעות תחומי בלוקים
הערה: כדי לבנות את גיאומטריית המודל, נעשה שימוש בשלושה בלוקים לייצוג מבנים שונים בעין. בלוק 1 ייצג את הכורואיד, בלוק 2 את רקמת הרשתית, ובלוק 3 את הזגוגית.- לחץ לחיצה ימנית על גיאומטריה 1 > בלוק כדי ליצור תחום בלוק. חזור על שלב זה פעמיים נוספות כדי ליצור שלושה בלוקים בסך הכל. לכל הבלוקים, קבעו הן את העומק והן את הרוחב ל- 5,000 מיקרומטר, ושנו את האפשרות 'בסיס' (תחת 'מיקום') ל'מרכז'. הקצה את ערכי הגובה (תחת גודל וצורה) ו- z (תחת מיקום) הבאים עבור כל בלוק:
בלוק 1: גובה = 112 מיקרומטר, z = 0 מיקרומטר
בלוק 2: גובה = 151 מיקרומטר, z = 131.5 מיקרומטר
בלוק 3: גובה = 5,000 מיקרומטר, z = 2,707 מיקרומטר
- לחץ לחיצה ימנית על גיאומטריה 1 > בלוק כדי ליצור תחום בלוק. חזור על שלב זה פעמיים נוספות כדי ליצור שלושה בלוקים בסך הכל. לכל הבלוקים, קבעו הן את העומק והן את הרוחב ל- 5,000 מיקרומטר, ושנו את האפשרות 'בסיס' (תחת 'מיקום') ל'מרכז'. הקצה את ערכי הגובה (תחת גודל וצורה) ו- z (תחת מיקום) הבאים עבור כל בלוק:
- יצירת תוכנית עבודה להוספת אלקטרודה למודל
- לחצו לחיצה ימנית על גיאומטריה 1 בעץ הדגם, ובחרו 'מישור עבודה'. לחץ על מישור עבודה 1 ושנה את סוג המישור לפנים מקבילות, לחץ על כפתור הפעל בחירה מתחת לסוג המישור ובחר את המשטח התחתון של בלוק 1 (blk 1 > 1).
- ציור אלקטרודת דיסק במישור העבודה
- לחץ על גיאומטריה מישורית תחת מישור עבודה 1 ולחץ על סקיצה בסרגל הכלים הראשי. בחרו ' עיגול', לחצו במקום כלשהו בתוך המלבן בכרטיסייה ' גרפיקה' וגררו ליצירת אלקטרודת דיסק. שנה את הרדיוס ל- 'elec_rad' μm, xw ו- yw ל- 0 μm ולאחר מכן לחץ על בנה הכל.
- הקצאת תכונות חומר לכל תחום
הערה: על-ידי ביצוע השלבים לבניית הגיאומטריה, המודל יופרד למספר 'תחומים', שהם חלקים תלת-ממדיים בודדים המרכיבים את הגיאומטריה השלמה. לכל תחום יש להקצות ערך מוליכות חשמלית כדי לחשב את התפלגות השדה החשמלי בכל המודל.- בעץ הדגם, לחץ באמצעות לחצן העכבר הימני על חומר > חומר ריק ולאחר מכן לחץ על חומר 1 ושנה את הבחירה לידנית.
- לחץ על הדומיינים בחלון גרפיקה כך שרק תחום 1 ייבחר. בחר תכונות חומר > תכונות בסיסיות > מוליכות חשמלית, לחץ על הוסף לחומר לחצן ושנה את ערך המוליכות החשמלית לערך ל- 0.043 S/m15.
- חזור על השלבים עבור תחומים 2 ו- 3, עם ערכי המוליכות החשמלית של 0.7 16 ו- 1.5516 S/m, בהתאמה (איור משלים 3).
- שילוב מודל תלת-ממדי: כדי לרשת את המודל, עבור אל עץ המודל ולחץ באמצעות לחצן העכבר הימני על Mesh 1 > Free Tetrahedral. לחץ על Tetrahedral חינם 1 ובחר בנה הכל.
הערה: תהליך הרשת מפרק את כל הגיאומטריה ל'אלמנטים' קטנים יותר (אלמנט הוא קטע וירטואלי בגאומטריה של המודל שבו המשוואות הפיזיקליות נפתרות באופן מספרי). שילוב עם אלמנטים קטנים יותר מגדיל באופן תיאורטי את דיוק הקירוב אך הוא ממצה מבחינה חישובית. נוהג נפוץ הוא להתחיל את המודל עם רשת דלילה ולרשום את התוצאה של הסימולציה, ולאחר מכן לחזור ברציפות על הסימולציה עם רכיבי רשת קטנים יותר בכל פעם ולהשוות את התוצאות. תהליך העידון יכול להיפסק כאשר אין הבדל משמעותי בתוצאות החישוב משלבי העידון הבאים.- הערכת איכות הרשת: לחצו לחיצה ימנית על Mesh 1 ובחרו 'סטטיסטיקה ' כדי להציג את ההיסטוגרמה של איכות האלמנט. בצע את שלבי זיקוק הרשת שלהלן כדי לשפר את איכות האלמנטים.
הערה: שימוש ברשת השינוי המוגדרת כברירת מחדל עלול ליצור רכיבים רבים באיכות נמוכה, אשר בתורם מעבדים חישובים לא מדויקים. ברוב המקרים, יש צורך במידה מסוימת של עידון רשת. - עידון הרשת סביב היקף האלקטרודה
הערה: האזורים שבהם עשויים להיות שינויים פתאומיים בשדה החשמלי דורשים בדרך כלל רשת מעודנת יותר. כאן נוספה רשת צפופה יותר סביב היקף האלקטרודה באמצעות תכונת חלוקת הקצה.- ראשית, מחק את רשת Tetrahedral 1 הקיימת בחינם. לאחר מכן, לחץ לחיצה ימנית על רשת 1 > התפלגות, לחץ על התפלגות 1, שנה את רמת הישות הגיאומטרית לקצה ובחר קצוות 19-22 (היקף אלקטרודת הדיסק).
- הגדר את סוג ההתפלגות למספר קבוע של רכיבים ושנה את השדה מספר רכיבים ל- elec_rad*3/10 כדי להפוך את הרכיבים לקטנים במידה סבירה.
- עידון הרשת על פני הכורואיד ורקמת הרשתית
- בעץ הדגם, לחץ באמצעות לחצן העכבר הימני על Mesh 1 > נסחף. לחץ על סחף 1. בחר תחומים 1 ו- 2. לאחר מכן, לחץ באמצעות לחצן העכבר הימני על MeSH 1 > Free Tetrahedral, הגדר את רמת הישות הגיאומטרית לשאריות, ולחץ על בנה הכל. (אופציונלי: בדוק שוב את ההיסטוגרמה של איכות הרכיב כדי לוודא שהרכיבים באיכות נמוכה הופחתו בפרופורציה).
- הערכת איכות הרשת: לחצו לחיצה ימנית על Mesh 1 ובחרו 'סטטיסטיקה ' כדי להציג את ההיסטוגרמה של איכות האלמנט. בצע את שלבי זיקוק הרשת שלהלן כדי לשפר את איכות האלמנטים.
- הגדרת מודל FEM בממשק המשתמש הגרפי (GUI) של התוכנה:
- החלת הפיזיקה על מודל האלמנטים הסופיים
הערה: ה'פיזיקה' בתוכנת FEM הן קבוצות של משוואות מתמטיות ותנאי גבול שיש להקצות למודל. זהו חישוב הפתרון למערכת המשוואות בו זמנית המתבצעת במהלך הפעלת המודל. בחירת הפיזיקה ליישם את הגיאומטריה תלויה בתופעה הפיזיקלית המדומה. לדוגמה, פיזיקת הזרם החשמלי, כפי שהיא משמשת במודל זה, מתבוננת בחלוקת השדה החשמלי ומזניחה את התופעה המגנטית (האינדוקטיבית). פיזיקה אחרת יכולה להיות מיושמת על הגיאומטריה אם בעיות פיזיקליות אחרות (למשל, התפלגות טמפרטורה, לחץ מכני וכו ') ייפתרו.- בחירת פיזיקה ויישום תנאי גבול
הערה: אם יש להחיל פולס מתח קבוע, יש להחליף את תנאי הגבול הפוטנציאלי הצף בתנאי גבול פוטנציאלי חשמלי.- הרחב את זרמים חשמליים 1 בעץ המודל ובדוק אם שימור זרם 1, בידוד חשמלי 1 וערכים התחלתיים 1 מפורטים. לאחר מכן, לחץ באמצעות לחצן העכבר הימני על הזרמים החשמליים 1 > הארקה (זה מקצה 0 V למישור מרוחק, המדמה אלקטרודת ייחוס מרוחקת) והחל זאת על פני השטח הרחוקים ביותר מהאלקטרודה (משטח 10).
- לאחר מכן, לחץ באמצעות לחצן העכבר הימני על הזרמים החשמליים 1 > פוטנציאל צף (זה מדמה מקור זרם עם זרם קבוע), שהוקצה לאלקטרודת הדיסק (משטח 14), ושנה את הערך I 0 ל- 1[μA] כדי להחיל זרם יחידתי.
- הרצת הסימולציה עם טאטוא פרמטרי.
הערה: שלב זה יפעיל את הסימולציה ונוסף טאטוא פרמטרי, שבו נעשו מספר סימולציות עם ערך של פרמטר שהשתנה בכל סימולציה. כאן, פרמטר רדיוס האלקטרודה נסחף והתפלגות הפוטנציאל החשמלי עבור כל סימולציה אוחסנה בקובץ המודל. לאחר הפעלת הסימולציה, ענף התוצאות בעץ המודל היה מאוכלס בגרף רב-פרוסות של פוטנציאל חשמלי (ec).- בעץ הדגם, לחץ באמצעות לחצן העכבר הימני על מחקר 1 > טאטוא פרמטרי. לחץ על טאטוא פרמטרי, ובטבלת הגדרת המחקר , לחץ על הוסף ולאחר מכן בחר elec_rad עבור שם הפרמטר.
- הקלד '50, 150, 350, 500' עבור רשימת ערכי הפרמטרים ו- 'μm' עבור יחידת הפרמטרים, ולחץ על מחשוב כדי להפעיל את המחקר (איור משלים 4).
- בחירת פיזיקה ויישום תנאי גבול

איור 1: יצירת הגיאומטריה של טיסו . גיאומטריית בלוקים הוכנסה למודל FEM כדי לייצג את הרקמה. אנא לחץ כאן כדי להציג גרסה גדולה יותר של נתון זה.
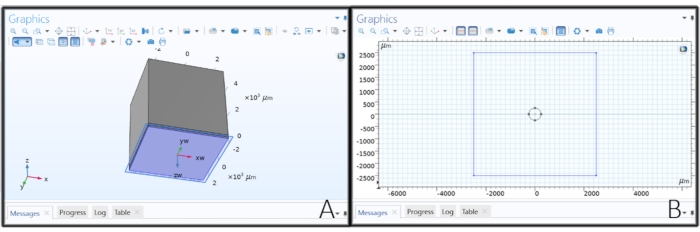
איור 2: יצירת הגיאומטריה של האלקטרודה . (A) יצירת מישור עבודה לציור אלקטרודת הדיסק. (B) שרטוט עיגול על מישור עבודה ליצירת אלקטרודת דיסק. אנא לחץ כאן כדי להציג גרסה גדולה יותר של נתון זה.

איור 3: היסטוגרמה של איכות האלמנט במודל FEM. ההיסטוגרמה הראתה את איכות האלמנטים ברחבי המודל. יש צורך בחידודים של רשת אם חלק ניכר מהאלמנטים נמצאים באזור באיכות נמוכה. אנא לחץ כאן כדי להציג גרסה גדולה יותר של נתון זה.
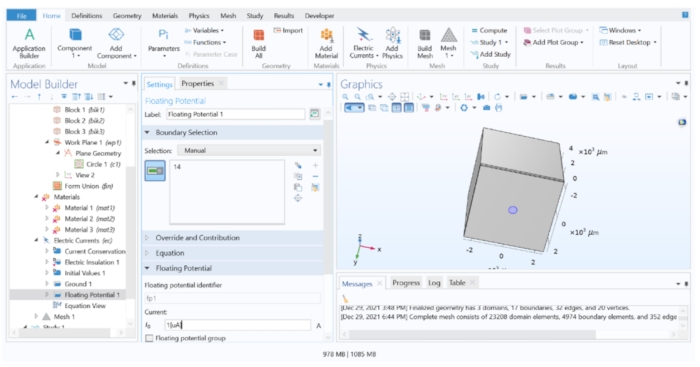
איור 4: הקצאת ערך נוכחי לאלקטרודה. זרם יוניטרי המיושם על הגיאומטריה של האלקטרודה בתוכנת FEM. אנא לחץ כאן כדי להציג גרסה גדולה יותר של נתון זה.
2. ייבוא הגיאומטריה של התא העצבי בממשק המשתמש הגרפי של חבילת הנוירונים
- בניית הגיאומטריה של מודל התא
- ייבוא המורפולוגיה באמצעות התכונה 'בונה תאים'.
- הפעל את 'nrngui' מתיקיית ההתקנה של חבילת הנוירונים החישובית, לחץ על כלים > שונות > ייבוא תלת-ממד ולאחר מכן סמן את התיבה בחר קובץ .
- אתר את קובץ ה- .swc שהורדת ולחץ על קריאה. לאחר ייבוא הגיאומטריה, לחץ על ייצוא > בונה התאים (איור משלים 5).
- יצירת קובץ .hoc של מורפולוגיה של התא המיובא
- עבור אל הכרטיסייה Subsets והתבונן בתת-הקבוצות שהוגדרו מראש במודל (לדוגמה, סומה, אקסון, בסיס וכו'). סמן את התיבה יצירה רציפה , עבור אל ניהול > ייצוא וייצא את המורפולוגיה כ- 'rgc.hoc'.
- הצגת המורפולוגיה של התא
- לחץ על Tool > Model View > 1 תאים אמיתיים > שורש סומה[0] בסרגל הכלים, לחץ באמצעות לחצן העכבר הימני על החלון המופיע ולחץ על ציר סוג > הצג ציר. על ידי בדיקה חזותית, קוטר השדה הדנדריטי של דגם זה הוא בסביבות 250 מיקרומטר. סגור את חלונות הנוירונים לעת עתה.
- ייבוא המורפולוגיה באמצעות התכונה 'בונה תאים'.

איור 5: ייצוא מידע על מודל הנוירונים כקובץ .hoc. הגיאומטריה של הנוירון יוצאה לקובץ .hoc כדי לאפשר שינויים נוספים. אנא לחץ כאן כדי להציג גרסה גדולה יותר של נתון זה.
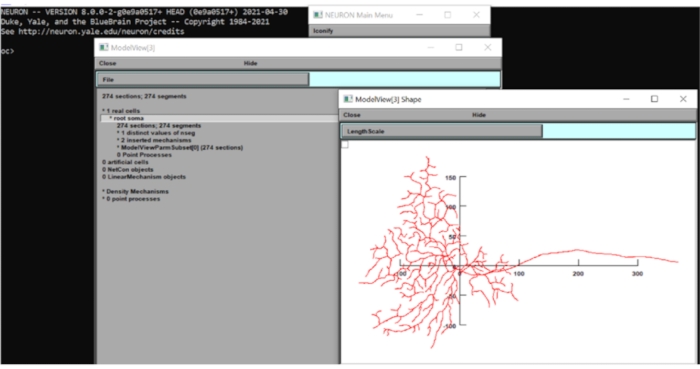
איור 6: מדידת הממד של תא העצב. המורפולוגיה של הנוירון (מבט עליון) הוצגה בממשק המשתמש הגרפי של חבילת הנוירונים החישובית עם צירי x-y על גבי. קנה המידה היה ב-μm. אנא לחץ כאן כדי להציג גרסה גדולה יותר של נתון זה.
3. תכנות סימולציית החישוב של NEURON
- התאמת המורפולוגיה של התא על-ידי תכנות בשפת .hoc
הערה: ניתן לכוונן את המורפולוגיה של התא באמצעות התכונה 'בונה תאים' של ממשק המשתמש הגרפי. עם זאת, כיצד ניתן לעשות זאת על ידי עריכת קובץ ה- .hoc כדי להאיץ את התהליך מודגם. קובץ ההוק מגדיר את הטופולוגיה (קשרים פיזיקליים בין כל חלק של הנוירונים), את המורפולוגיה (האורך, הקוטר והמיקום של כל מקטע נוירון) ואת התכונות הביופיזיות (פרמטרים של תעלת יונים) של התא הממודל. את התיעוד המלא עבור תכנות .hoc ניתן למצוא ב: https://neuron.yale.edu/neuron/static/new_doc/index.html#,- פתח את קובץ ה- .hoc שנוצר באמצעות עורך טקסט (לדוגמה, פנקס רשימות). הוסף מקטע ראשוני של אקסון באורך 40 מיקרומטר וקטע אקסונאלי צר באורך 90 מיקרומטר קרוב לסומה כמתואר ב-Sheasby וב-Fohlmeister17, וכן שנה את אורך הדנדריטים כך שגודל השדה הדנדריטי יהפוך ל-180 μm כך שיתאים לתא G1 ברוקהיל, et al.18.
- יצירת מקטעי תא חדשים והגדרת הקשרים הטופולוגיים עבור כל מקטע.
- כדי ליצור מקטעי תא חדשים עבור המקטע ההתחלתי של האקסון (AIS) והמקטע האסוני הצר (NS), הוסף שורות אלה לתחילת הקובץ rgc.hoc:
יצירת AIS, NS // הכרזה על תאי תאים הנקראים AIS ו- NS
לאחר מכן, החלף את הקו 'חבר אקסון(0), סומה[1](1)' ב:
connect ais(0), soma[1](1) // חיבור המקטע הראשון של AIS לסוף סומה[1]
חיבור ns(0), ais(1) // חיבור הקטע הראשון של NS לסוף AIS
חיבור אקסון(0), ns(1) // חיבור הקטע הראשון של האקסון לסוף NS
- כדי ליצור מקטעי תא חדשים עבור המקטע ההתחלתי של האקסון (AIS) והמקטע האסוני הצר (NS), הוסף שורות אלה לתחילת הקובץ rgc.hoc:
- הגדרת המיקומים, הקטרים והאורך התלת-ממדיים של מקטעי התא
- הגדר את המיקומים והקטרים התלת-ממדיים של תאי AIS ו- NS על-ידי כתיבת שורות אלה בתוך סוגריים 'proc shape3d_31()':
ais { pt3dadd(-2.25, -1.55, 0, 1) // שלושת המספרים הראשונים הם קואורדינטת xyz, והקוטר הוא 1 מיקרומטר
pt3dadd(37.75, -1.55, 0, 1)} // הנקודה הראשונה היא ב- x = -2.25 מיקרומטר והנקודה האחרונה היא ב- x = 37.75 מיקרומטר
ns { pt3dadd(37.75, -1.55, 0, 0.3) // הקואורדינטות התלת-ממדיות והקוטר של מקטעי ה-NS
pt3dadd(127.75, -1.55, 0, 0.3)} - בסוף הקובץ, הזז את הקואורדינטות התלת-ממדיות של האקסון כך שהנקודה הראשונית שלו תפגוש את נקודת הקצה של NS על-ידי הקלדה:
axon {for i=0,n3d()-1 {pt3dchange(i, x3d(i)+130, y3d(i),z3d(i)-5, diam3d(i))}} //Shift the x-coordinate - בסוף הקובץ, קצר את התאים הדנדריטיים ב-18% על ידי הקלדה:
forsec baseal {L=L*0.82} // שינוי קנה המידה של האורך כדי להקטין את גודל השדה הדנדריטי
define_shape() // מילוי מידע תלת-ממדי חסר
- הגדר את המיקומים והקטרים התלת-ממדיים של תאי AIS ו- NS על-ידי כתיבת שורות אלה בתוך סוגריים 'proc shape3d_31()':
- יצירת מקטעי תא חדשים והגדרת הקשרים הטופולוגיים עבור כל מקטע.
- פתח את קובץ ה- .hoc שנוצר באמצעות עורך טקסט (לדוגמה, פנקס רשימות). הוסף מקטע ראשוני של אקסון באורך 40 מיקרומטר וקטע אקסונאלי צר באורך 90 מיקרומטר קרוב לסומה כמתואר ב-Sheasby וב-Fohlmeister17, וכן שנה את אורך הדנדריטים כך שגודל השדה הדנדריטי יהפוך ל-180 μm כך שיתאים לתא G1 ברוקהיל, et al.18.
- הגדרת מספר המקטעים עבור כל מקטע
הערה: כל מקטע של תא העצב יכול להיות בדיד מרחבית, בדומה לתהליך הרשת במודל FEM. הדיסקרטיזציה המרחבית מחלקת את הנוירון כמעט למקטעים קטנים יותר שבהם יש לבצע חישובים. עבור מספר המקטעים 'nseg', ודא שמספרים אי-זוגיים משמשים כדי להבטיח שיש צומת פנימי בנקודת האמצע של מקטע תא, ונסה לשלש את מספר nseg עד שהחישוב יניב תוצאה עקבית9. מספר גבוה יותר של מקטעים יפיק קירוב מספרי מדויק יותר אך גם יגדיל את העומס החישובי.- כדי להדגים את תהליך הבדידה, הוסף את השורות הבאות בקובץ rgc.hoc כדי לחלק את החלקים העצביים בתת-הקבוצות הסומטיות והאקסונאליות למספר מקטעים:
Forsec somatic {NSEG=31}
Forsec axonal {NSEG=301}
חלקים אחרים במודל צריכים להיות נפרדים גם כן על ידי הקלדת שורות אלה אך שינוי שם תת-הקבוצה (לאחר 'forsec') ומספר הקטעים (לאחר 'nseg') לפי הצורך.
- כדי להדגים את תהליך הבדידה, הוסף את השורות הבאות בקובץ rgc.hoc כדי לחלק את החלקים העצביים בתת-הקבוצות הסומטיות והאקסונאליות למספר מקטעים:
- הוספת מנגנוני תעלת יונים מותאמים אישית
- כתיבת מנגנוני תעלת יונים מותאמים אישית כקבצי .mod: כדי להחיל את מנגנוני תעלת היונים, צור קבצי .mod והכנס את הקבצים לחלק הביופיזי של קובץ ה- .hoc על-ידי ביצוע השלבים 3.3.1-3.3.3. קובץ ה- .mod מכיל את המשתנים ואת המשוואות הדיפרנציאליות שיש לפתור עבור כל תעלת יונים.
הערה: הגדרות ויישומים נכונים של מנגנון תעלת יונים הם קריטיים בהדמיות מדויקות של תאי עצב. בעת כתיבת קבצי .mod, בדוק אם היחידות נכונות (כלי השירות 'modlunit' המסופק שניתן להפעיל כדי לבדוק עקביות יחידות) וכי המשוואות נכתבות כהלכה. כדי לבדוק שמנגנוני תעלת היונים נכונים, ניתן לשרטט את הזרם של כל תעלת יונים במהלך גירוי תוך-תאי או חוץ-תאי ולהשוות אותו לממצאים אמפיריים.- תעלות יונים מגודרות מתח
הערה: קובץ .mod ליצירת תעלת יונים מגודרת מתח כולל בדרך כלל בלוק DERIVATIVE הכולל את המשוואה הדיפרנציאלית לפתרון, בלוק BREAKPOINT הכולל את הפקודות לפתרון המשוואות הדיפרנציאליות באמצעות שיטת קירוב נומרית שנבחרה, וגושי PROCEDURE המורים לתוכנית לחשב את הפרמטרים של gating (לדוגמה, mt, ht ו- d בדוגמה זו). קוד זה יחשב את ערכי הזרם היוני העובר דרך הערוץ עבור כל שלב זמן.- כדי להדגים את התהליך, צור תעלת Ca תלוית מתח הכוללת משוואות דיפרנציאליות מסדר ראשון לפתרון עבור המשתנים המשתנים.
- פתח קובץ חדש בעורך הטקסט והקלד את השורות בערוץ Cat המשלים המגדיר חומר תלוי-מתח. שמור קובץ זה כ- Cat.mod באותה תיקיה שבה נמצא קובץ ה- .hoc. יש לחזור על תהליך זה עבור תעלות היונים האחרות שתא העצב המודל מכיל.
- תעלות יונים תלויות מתח וריכוז
- הקינטיקה של חלק מתעלות היונים, כגון תעלות האשלגן המופעלות על ידי סידן בתאי הגנגליון ברשתית, תלויה בריכוז הסידן התוך-תאי מלבד המתח הטרנס-ממברני19. כדי ליצור מודל של מנגנון מסוג זה, צור קובץ בשם KCa.mod, והקלד את השורות כפי שמוצג בתעלות יונים תלויות מתח וריכוז של חומרים משלימים. בקובץ .mod זה חושב המשתנה 'cai', המוגדר כריכוז הפנימי של יון Ca, ולאחר מכן משתנה זה משמש במשוואה לחישוב זרם iKCa.
- תעלות יונים מגודרות מתח
- אוסף של קבצי .mod
- הדר את כל קבצי ה- .mod על-ידי הפעלת כלי השירות mknrndll של חבילת הנוירונים מתיקיית ההתקנה. אתר את התיקיה שבה נמצאים קבצי ה- .mod ולחץ על הידור כדי ליצור קבצי O ו- C. לאחר מכן, המנגנונים יכולים להיות מוכנסים לתוך מודל התא הזה.
- יישום של קבצי .mod בקובץ המודל הראשי של NEURON.
הערה: מלבד הכנסת תעלות היונים, מוליכות Na המרבית הוגדרה עבור תת-הקבוצה 'סומטית' בלבד. אנו יכולים להתאים בנפרד את מוליכות הממברנה המרבית עבור מקטעים עצביים שונים במידת הצורך.- לקיצור, שלב את כל מנגנוני תעלת היונים לקובץ .mod יחיד (קובץ .mod של חומר משלים-שלם). הוסף את קובץ ה- .mod המשולב המכיל את כל ערוצי היונים ותעלת דליפה פסיבית לכל המקטעים בתת-הקבוצה 'סומטית' על ידי הקלדת השורות שלהלן בהליך 'ביופיס' של הקובץ rgc.hoc:
forsec somatic {insert rgcSpike
הכנס PAS // ערוץ דליפה פסיבי
gnabar_rgcSpike = 80e-3
g_pas = 0.008e-3 // מוליכות ממברנת דליפה}
- לקיצור, שלב את כל מנגנוני תעלת היונים לקובץ .mod יחיד (קובץ .mod של חומר משלים-שלם). הוסף את קובץ ה- .mod המשולב המכיל את כל ערוצי היונים ותעלת דליפה פסיבית לכל המקטעים בתת-הקבוצה 'סומטית' על ידי הקלדת השורות שלהלן בהליך 'ביופיס' של הקובץ rgc.hoc:
- הגדרת ההתנגדות האקסופלסמית
- לתאים יש התנגדות אקסופלסמית הניתנת לשינוי בכל תא. עבור מודל זה, לכל הקטעים יש התנגדות זהה של 110 Ω·cm. שנה את ההתנגדות האקסופלסמית בקובץ rgc.hoc:
forall {Ra = 110}
- לתאים יש התנגדות אקסופלסמית הניתנת לשינוי בכל תא. עבור מודל זה, לכל הקטעים יש התנגדות זהה של 110 Ω·cm. שנה את ההתנגדות האקסופלסמית בקובץ rgc.hoc:
- כתיבת מנגנוני תעלת יונים מותאמים אישית כקבצי .mod: כדי להחיל את מנגנוני תעלת היונים, צור קבצי .mod והכנס את הקבצים לחלק הביופיזי של קובץ ה- .hoc על-ידי ביצוע השלבים 3.3.1-3.3.3. קובץ ה- .mod מכיל את המשתנים ואת המשוואות הדיפרנציאליות שיש לפתור עבור כל תעלת יונים.
- הכנס מנגנונים חוץ-תאיים והגדר צורת גל של דופק
- החדרת מנגנון חוץ-תאי למודל התא
- כדי שמודל התא יגיב למתח חוץ-תאי, הכנס מנגנון חוץ-תאי לכל המקטעים על-ידי הקלדת השורה בתחתית הקובץ rgc.hoc:
forall {הכנס חוץ-תאי}
- כדי שמודל התא יגיב למתח חוץ-תאי, הכנס מנגנון חוץ-תאי לכל המקטעים על-ידי הקלדת השורה בתחתית הקובץ rgc.hoc:
- יצירת דופק דו-פאזי
הערה: בהדגמה זו, נוצר פולס דו-פאזי זרם קבוע הניתן להתאמה על-ידי המשתמש ברוחב הפולס, במרווח האינטרפאזה ובמספר החזרות על-ידי יצירת פרוצדורה בקובץ .hoc. עבור תוכנית מובנית יותר, השתמש בקובץ rgc.hoc כקובץ ליצירת מודל התא, בעוד שתהליך הגירוי מוחל בקובץ .hoc נפרד, אשר יטען את מודל התא שעליו מוחל הגירוי.- צור קובץ טקסט חדש בשם stimulation.hoc והתחל את הקוד על ידי טעינת קובץ מודל התא; לאחר מכן, צור פולס דו-פאזי על-ידי הגדרת הליך כפי שמוצג בחומר משלים - יצירת פולס דו-פאזי בסימולציית הנוירונים.
הערה: שלב זה יוצר פולס דו-פאזי קבוע של זרם קתודי-ראשון, שבו הפרמטרים של הגירוי אמורים להיות מוכרזים על-ידי המשתמש בעת הפעלת הסימולציה. נכון לעכשיו, גודל הפולסים האנודיים והקתודיים הוא ±1 μA, אך גודל זה צריך להשתנות בהתאם לזרם הגירוי המועבר על ידי אלקטרודת הדיסק.
- צור קובץ טקסט חדש בשם stimulation.hoc והתחל את הקוד על ידי טעינת קובץ מודל התא; לאחר מכן, צור פולס דו-פאזי על-ידי הגדרת הליך כפי שמוצג בחומר משלים - יצירת פולס דו-פאזי בסימולציית הנוירונים.
- החדרת מנגנון חוץ-תאי למודל התא
4. הפעלה ואוטומציה של סימולציות מרובות
- שילוב המודלים
- חילוץ הקואורדינטות עבור הצמתים במודל תא העצב
הערה: מטרת שילוב הסימולציות היא לרכוש את ערכי הפוטנציאל החוץ-תאי המתאימים לכל צומת במודל התא. עם זאת, הקואורדינטות של שני המודלים חייבות להיות מיושרות. בדוגמה זו, הקטע המרכזי של הסומה (soma(0.5)) היה מיושר כדי לשכב על האמצע האופקי של רקמת הרשתית (המתאים לשכבת תאי הגנגליון ברשתית), כאשר הצומת המרכזי של הסומה ממוקם ממש מעל מרכז אלקטרודת הדיסק.- פתח את מודל FEM, ושים לב לקואורדינטות של נקודת התייחסות (לדוגמה, האמצע האופקי של רקמת הרשתית, מעל מרכז אלקטרודת הדיסק), ובמקרה זה היא [0, 0, 131.5] μm.
- בחבילה החישובית של הנוירונים, צור קובץ שנקרא calculateCoord.hoc כדי לחלץ את הקואורדינטות של הצנטרואיד של כל מקטע ולהזיז כל מקטע כך שלמקטע המרכזי של הסומה תהיה אותה קואורדינטות כמו נקודת הייחוס במודל FEM (חומר משלים - חישוב הקואורדינטות של כל צומת).
- שמירת נקודות הקואורדינטות בקובץ טקסט
- הפעל את הקובץ calculateCoord.hoc (על ידי לחיצה כפולה מסייר הקבצים או על ידי פתיחת GUI של חבילת החישובים של הנוירונים; לאחר מכן, לחץ על קובץ > לטעון הוק בסרגל הכלים). שמור את הקואורדינטות עבור ערכי המתח החוץ-תאי שיוערכו בקובץ טקסט בשם 'קואורדינטות.dat'.
- הרצת ההדמיות ושמירת נתוני המתח לקובץ טקסט
הערה: בשלב זה, חילצנו את הערכים החוץ-תאיים המחושבים ממודל FEM, אך היינו שומרים את הנתונים רק מהקואורדינטות הרלוונטיות שעולות בקנה אחד עם המרכז של כל מקטע תא. בצע את שלב 4.1.6.2 כאשר נדרש מספר רב של פוטנציאלים לייצוא.- פתח את קובץ מודל הרקמות בתוכנת FEM; עבור אל הכותרת תוצאות בעץ המודל ולחץ על ייצוא נתוני > > נתונים 1. ודא שערכת הנתונים מוגדרת ללמוד 1/פתרונות פרמטריים 1 ולאחר מכן הקלד 'V' בעמודה ביטוי ו- 'mV' בעמודה יחידה.
- תחת פלט, שנה את שם הקובץ לחוץ.dat, ובחר נקודות להערכה: מקובץ. טען את הקואורדינטות.dat עבור השדה קובץ קואורדינטות ולאחר מכן לחץ על ייצוא.
- החלת הדופק הדו-פאזי על מודל התא
הערה: בשלב זה, ערכי המתח החוץ-תאי עבור כל מקטע תא בנקודת זמן אחת (כאשר הזרם הוא 1 μA) זמינים. מכיוון שהמחקר מתכוון להכפיף את התא לפולס דו-תאי, לגרום לערך המתח החוץ-תאי שחווה התא להשתנות עם הזמן באמצעות השיטה 'vector.play'.- הוסף את הקווים המוצגים בחומר המשלים - יישום של הדופק הדו-פאזי בגירוי.הוק.
- הרצת הסימולציה המשולבת
הערה: יש להגדיר מרווח זמן 'dt' עבור הקירובים המספריים כדי להפעיל את הסימולציות. בדומה ל- nseg, dt קצר יותר יכול להגדיל את הדיוק החישובי אך גם להגדיל את העלות החישובית.- הוסף את הקווים המוצגים בחומר המשלים - ביצוע סימולציית הנוירון לסוף הגירוי.הוק. לאחר מכן, לחץ פעמיים על הקובץ stimulation.hoc כדי לטעון את הסקריפט ולהפעיל באופן אוטומטי את הסימולציה. ניתן להציג את הפוטנציאל הטרנס-ממברני של מקטע העניין בממשק המשתמש הגרפי של חבילת הנוירונים (שלב 4.2.1) או לשמור אותו בקובץ טקסט לקריאה בתוכניות אחרות (שלב 4.1.6.1.2). בצע את השלבים 4.1.6.1 ו- 4.1.6.2 אם יש צורך לייצא חישובים חוזרים ומספר רב של פוטנציאלים של ממברנה.
- אקסטרה: אוטומציה של סימולציות
הערה: כדי למצוא משרעת סף, הפעל את הסימולציה מספר פעמים בלולאה עם משרעת זרם שונה בכל פעם. ייתכן שיהיה צורך באוטומציה נוספת כדי למצוא את הסף עבור תאי עצב הממוקמים במיקומים שונים ביחס לאלקטרודה המגרה. ניתן לבצע שלב אוטומציה בחבילת החישובים של הנוירונים באמצעות פרוצדורה, כמו גם בתוכנת FEM באמצעות סקריפט הנקרא 'שיטה'.- אוטומציה של סימולציית נוירונים למציאת משרעת סף
הערה: ניתן לבצע אצווה של סימולציות נוירונים באופן אוטומטי. השלבים הבאים מיושמים בתוכנית סימולציית הנוירונים כדי למצוא את משרעת הסף של נוירונים תחת פרמטרים שונים של גירוי.- צור הליך לחזרה על סימולציה בתוכנית סימולציית נוירונים: ב- stimulation.hoc, צור וקטור שיכיל טווח של משרעת זרם לבדיקה. לאחר מכן, צור הליך להחלת משרעת הזרם ורישום כל נוכחות של ספייק (שינוי חיובי ממתח טרנס-ממברנה שלילי לחיובי), ומשרעת הסף מוגדרת כמשרעת הזרם הנמוכה ביותר הגורמת להופעת ספייק. לשם כך, הגדר הליך הנקרא findTh() (לולאת חומר משלימה על פני טווח של אמפליטודות זרם) בסוף הקובץ stimulation.hoc
- שמירת התגובה בסף לקובץ טקסט: הוסף את השורות הבאות לפרוצדורה findTh() ב- stimulation.hoc כדי לאחסן את ערכי המתח הטרנס-ממברניים המחושבים עבור כל תאי הנוירונים מכל שלב בקובץ טקסט:
sprint(saveFileName, "Response_%d.dat", th) // אחסן את ערך הסף
saveFile.wopen(saveFileName)
for i=0,(responseVector.size()-1){
saveFile.printf("%g, ", responseVector.x[i])
if(i==responseVector.size()-1) {saveFile.printf("%g\n", responseVector.x[i])
saveFile.close(saveFileName)
}}
- אוטומציה בתוכנת FEM למציאת ערכי המתח עבור נוירונים במיקומים שונים
הערה: אוטומציה נוספת שניתן לבצע היא רכישה אוטומטית של ערכי מתח חוץ-תאיים עבור נוירונים במיקומים שונים. תפריט בונה היישומים בתוכנת FEM מספק אמצעי להגדרת 'שיטה', או סקריפט כדי להפוך את השלבים הדרושים לביצוע חישובים לאוטומטיים. כדי להדגים, מיקום התא בכיוון x מוסט פי 5 בצעד של 100 מיקרומטר (איור משלים 6).- כתיבת קוד לאוטומציות של הדמיות FEM.
- עבור אל בונה היישומים, לחץ באמצעות לחצן העכבר הימני על שיטות בעץ בונה היישומים, בחר שיטה חדשה ולחץ על אישור. עבור אל קובץ > העדפות > שיטות, סמן את הצג את כל הקודים תיבה ולחץ על אישור.
- כתוב סקריפט .hoc שיטען את קובץ הקואורדינטות, יזיז את הערכים כך שיתאימו למיקום הרצוי וישמור קובץ טקסט המכיל את ערכי המתח עבור המיקום החדש של התא על-ידי הקלדת הקודים המוצגים בשיטה להגדרת חומר משלים לאוטומציה של הדמיות FEM.
- הפעלת השלבים האוטומטיים בתוכנת FEM: עבור אל בונה המודלים, מפתח > שיטת הפעלה > שיטה 1. פעולה זו תפיק קבצי .dat עם ערכי המתח המתאימים, בשם extracellular_1.dat, extracellular_2.dat וכו '.
- כתיבת קוד לאוטומציות של הדמיות FEM.
- לולאה של הסימולציות בשפת תכנות לשימוש כללי
הערה: כדי לבצע את הסימולציות בלולאה, יש לטעון את קובץ הטקסט המתאים לסימולציה של חבילת הנוירונים בכל פעם, ושפת תכנות20 שיכולה לטעון ולתפעל קבצי טקסט בקלות נוחה לביצוע שלב זה. ניתן להשתמש בכל סביבת פיתוח משולבת נוחה (IDE)21 עבור שלב זה.- פתח את ה- IDE שנבחר, לחץ על קובץ חדש כדי ליצור סקריפט חדש . כאן נעשה שימוש בקובץ .py בדוגמה זו. הקלד את השורות המוצגות בחומר משלים - הפעלת הסימולציות בשפת תכנות למטרות כלליות.
- לבסוף, לחץ על הפעלה או הקש F5 כדי להפעיל את הסקריפט, אשר יפתח גם את ממשק המשתמש הגרפי (איור משלים 7).
- אוטומציה של סימולציית נוירונים למציאת משרעת סף
- חילוץ הקואורדינטות עבור הצמתים במודל תא העצב
- הצגת נתוני סימולציה
הערה: על-ידי ביצוע כל השלבים לעיל, יש לאחסן את תוצאות הסימולציה בקבצי טקסט, המכילים את ערך הסף ואת פוטנציאל הטרנס-ממברנה שבסף. עם זאת, למשתמש יש אפשרות להציג את תוצאת הסימולציה בזמן שהסימולציה פועלת באמצעות ממשק המשתמש הגרפי של NEURON.- גרף את התגובה של מודל הנוירונים לגירוי החוץ-תאי בממשק המשתמש הגרפי של חבילת הנוירונים. לשם כך, הפעל את stimulation.hoc, לחץ על גרף > ציר מתח מסרגל הכלים, ובחלון הגרף, לחץ לחיצה ימנית במקום כלשהו ובחר התווה מה.
- הקלד 'axon.v(1)' בשדה משתנה לגרף , כלומר הוא יתווה את פוטנציאל הטרנס-ממברנה של הקטע האחרון של האקסון לכל צעד זמן.
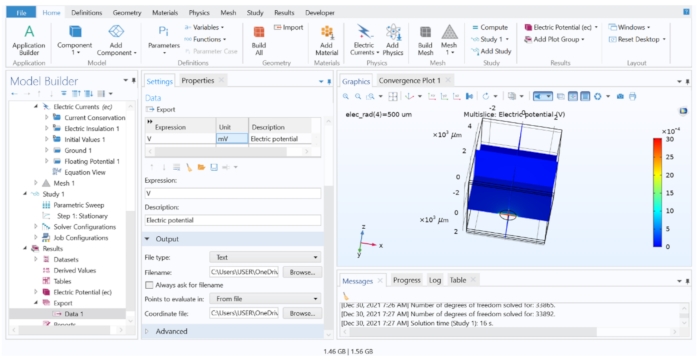
איור 7: הצגה וייצוא של תוצאות חישוב FEM לקובץ טקסט. החלון 'גרפיקה' המציג תרשים Multislice של הפוטנציאל החשמלי ב-V. האפשרויות בהגדרת ייצוא הנתונים אפשרו לייצא את המשתנה המחושב לקובץ טקסט. אנא לחץ כאן כדי להציג גרסה גדולה יותר של נתון זה.
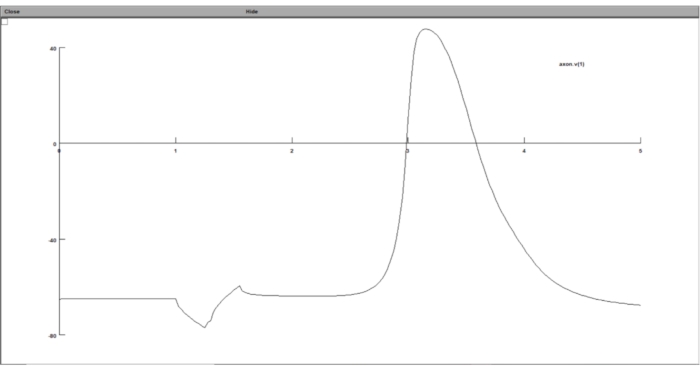
איור 8: הצגת הגרף של פוטנציאל הטרנס-ממברנה באמצעות גרף מתח. הפוטנציאל הטרנס-ממברני של הנוירונים הוצג בממשק המשתמש הגרפי של חבילת הנוירונים. ציר ה-x הוא הזמן ב-ms, בעוד שציר ה-y הוא הפוטנציאל הטרנס-ממברני של מקטע הנוירונים הנבחר ב-mV. אנא לחץ כאן כדי להציג גרסה גדולה יותר של נתון זה.
תוצאות
ערכנו שני פרוטוקולי סימולציה כדי להדגים את השימוש במודל. הפרוטוקול הראשון כלל שינוי גודל האלקטרודה תוך שמירה על מיקום תא העצב ופרמטרים של פולסים חשמליים זהים. הפרוטוקול השני כלל הסטת תא עצב בכיוון x בצעדים של 100 מיקרומטר, בעוד שגודל האלקטרודה נשאר קבוע. עבור שני הפרוטוקולים, הפולס שבו נעשה שימוש היה פולס דו-פאזי קתודי יחיד ברוחב 0.25 אלפיות השנייה עם מרווח אינטרפאזה של 0.05 אלפיות השנייה. עבור הפרוטוקול הראשון, רדיוס האלקטרודה שונה להיות 50, 150, 350 ו-500 מיקרומטר, ואילו עבור הפרוטוקול השני, רדיוס האלקטרודה נשמר על קבוע 50 מיקרומטר.
המודל המתואר כאן הראה שהגדלת גודל האלקטרודה העל-טבעית ברוחב פולס של 0.25 מילישניות הגדילה את סף ההפעלה של נוירון המודל (איור 9A). תוצאה זו שיקפה את ממצאי in vivo של Liang et al.12, שהראו כי סף ההפעלה בקליפת המוח עולה ככל שגודל האלקטרודה גדל ברוחב פולס זה.
סדרי הגודל של ספי ההפעלה של המודל שונים מהממצאים האמפיריים בגלל מספר גורמים. ראשית, מודל זה כולל רק RGC יחיד מסוג מסוים, אשר עשוי שלא להיות נוכח בקבוצת התאים המופעלים במחקר in vivo . לאחר מכן, מודל זה לא כלל רשת רשתית, אשר עשוי להקל על הפעלת RGCs באמצעות קלט מעורר מן התאים דו קוטביים. סיבה אפשרית נוספת לאי ההתאמה היא מרחק האלקטרודה-רשתית. ייתכן שמרחק האלקטרודה-רשתית במחקר in vivo היה נמוך יותר מאשר במודל זה עקב השתנות אנטומית או הניתוח. כתוצאה מכך, הערכנו יתר על המידה את מרחק האלקטרודה-רשתית ולכן את סף ההפעלה. חשוב גם לציין שלמרות שהדבר לא הודגם בתוצאות שלנו, מידול סף של תא בודד ימעיט לעתים קרובות בסף קליפת המוח in vivo . הסיבה לכך היא המגבלות הטכניות במדידות קליפת המוח (המתייחסות בעיקר ליחס האות לרעש) שהפעילות הקורטיקלית מתגלה בדרך כלל רק לאחר שהופעלו מספר תאי גנגליון ברשתית. כתוצאה מכך, יש לצפות לאי התאמה בגודל סף ההפעלה של הרשתית וקליפת המוח. למרות הבדלים אלה, מודל זה הראה בהצלחה את המגמה הגוברת של סף ההפעלה עקב הגידול בגודל האלקטרודה. זה נבע מהיעדר אזור של שדה חשמלי גבוה בהשוואה לסביבתו כאשר גודל האלקטרודה גדל, מה שלא העדיף הפעלה עצבית22.
לאחר מכן, צפינו במאפייני פוטנציאל הפעולה כדי לאמת את המודל המתואר כאן. ההשהיה, או הזמן שבין הופעת הגירוי לשיא פוטנציאל הפעולה, נע בין 1-2.2 מילישניות (איור 9B). זה תאם את ההשהיה הקצרה עקב הפעלת רשתית שאינה מתווכת רשת23. רוחב הספייק של דגם זה היה 1 אלפיות השנייה, וזה באותו טווח כמו רוחב הספייק של RGCs ארנב נמדד במבחנה24.
בפרוטוקול הגירוי השני, רק מיקום תא העצב בציר ה-x (לאורך האקסון) ביחס לאלקטרודה היה מגוון. במרחק 0, המרכז של קטע סומה היה מיד מעל מרכז אלקטרודת הדיסק. מרחק שלילי פירושו שאלקטרודת הדיסק הייתה ממוקמת קרוב יותר לצד האקסונאלי, בעוד שמרחק חיובי פירושו שאלקטרודת הדיסק הייתה ממוקמת קרוב יותר לצד הדנדריטי. המודל הראה כי הסף הנמוך ביותר הושג כאשר המקטע הצר של האקסון היה מיד מעל אלקטרודת הדיסק, והוא גדל ככל שמרחק ה-x נעשה גדול יותר (איור 9C). הזזת האלקטרודה לכיוון האקסון הדיסטלי יצרה סף נמוך יותר בהשוואה להזזת האלקטרודה לכיוון הדנדריטים בשל נוכחות המקטע הראשוני של האקסון והמקטע הצר שבו תעלות הנתרן שכיחות יותר. תוצאה זו הסכימה עם הממצא במבחנה של Jensen et al.13, שבו RGCs של ארנב היו מגורה עם מיקרואלקטרודה דקה במיוחד, וסף ההפעלה היה הגבוה ביותר כאשר האלקטרודה הוזזה קרוב יותר לדנדריטים.

איור 9: תוצאות שיטת המידול . (A) ספי ההפעלה של תא גנגליון ברשתית הממוקם מעל אלקטרודת הדיסק. רדיוס האלקטרודות היה מגוון (50, 150, 350 ו-500 מיקרומטר) והסף עלה עם הגדלת גודל האלקטרודה. (B) פוטנציאל הפעולה של מודל הנוירונים מתעצב ברוחב פולס של 0.25 אלפיות השנייה. פוטנציאל הפעולה בסף עבור גדלי אלקטרודות שונים הוא בעל רוחב ספייק זהה של 1 אלפיות השנייה, אך ההשהיה גדלה עם הגדלת גודל האלקטרודה. זמן הופעת הגירוי היה 1 אלפיות השנייה והשלב הקתודי גרם לדה-פולריזציה בממברנה אך לא מספיק כדי לגרום לפוטנציאל פעולה. (C) תא העצב הוזז לאורך ציר ה-x וסף ההפעלה הראה כי הסף הנמוך ביותר הושג על ידי תא העצב שהסומא שלו היה ממוקם ממש מעל מרכז האלקטרודה. רדיוס האלקטרודה היה 50 מיקרומטר. אנא לחץ כאן כדי להציג גרסה גדולה יותר של נתון זה.
איור משלים 1: אתחול מודל האלמנט הסופי. סוגי המחקר והפיזיקה קובעים את רשימת המשוואות הפתורות במודל. אלה הוגדרו במהלך היצירה הראשונית של קובץ המודל FEM, אך ניתן גם לשנות/להוסיף אותם לאחר יצירת המודל. אנא לחץ כאן כדי להוריד קובץ זה.
איור משלים 2: שינוי יחידת האורך. יחידת האורך והיחידה הזוויתית קובעות את היחידות המשמשות בתהליך הגדרת הגיאומטריה. אנא לחץ כאן כדי להוריד קובץ זה.
איור משלים 3: הכנסת תכונה חומרית. תכונות החומר הוגדרו עבור כל תחום במודל תלת-ממדי. תכונות החומר הזמינות נרשמו בחלון תכונות חומר בחלון הגדרת חומרים. לצורך חישוב הפוטנציאל החשמלי, הוגדרה רק התכונה מוליכות חשמלית. אנא לחץ כאן כדי להוריד קובץ זה.
איור משלים 4: יצירת מחקר פרמטרי כדי לעבור בלולאה על רשימה של ערכי פרמטרים. מחקר פרמטרי איפשר לתוכנת FEM לחזור באופן אוטומטי על החישובים ולשנות את ערך רדיוס האלקטרודה עבור כל חזרה. תוצאות החישוב אוחסנו עבור כל חזרה. אנא לחץ כאן כדי להוריד קובץ זה.
איור משלים 5: ייבוא המורפולוגיה של הנוירונים מקובץ SWC. החבילה החישובית של הנוירונים הייתה מסוגלת לקרוא קובץ SWC שנרכש ממעקב עצבי. הקובץ המיובא מכיל מידע על המורפולוגיה והטופולוגיה של כל מקטע נוירון. אנא לחץ כאן כדי להוריד קובץ זה.
איור משלים 6: אוטומציה של פעולות FEM על-ידי הגדרת שיטה. שיטה הוגדרה על ידי כתיבת סקריפט כדי להפוך תהליכים בתוכנת FEM לאוטומטיים שלא ניתן לעשות על ידי הגדרת מחקר פרמטרי. אנא לחץ כאן כדי להוריד קובץ זה.
איור משלים 7: שילוב המודלים ואוטומציה של הסימולציות באמצעות שפת תכנות למטרות כלליות. שפת התכנות למטרות כלליות שימשה ללולאה של סימולציות הנוירונים, תוך שינוי קובץ המתח החוץ-תאי המשמש כקלט וקובץ מתח התגובה העצבית כפלט עבור כל שלב בלולאה. אנא לחץ כאן כדי להוריד קובץ זה.
חומר משלים: שורות פקודה עבור (1) הגדרת ערוץ חתול תלוי מתח. (2) תעלות יונים תלויות מתח וריכוז. (3) קובץ .mod מלא. (4) יצירת פולס דו-פאזי בסימולציה של תא העצב. (5) חישוב הקואורדינטות של כל צומת. (6) יישום הדופק הדו-פאזי. (7) ביצוע סימולציית תא העצב. (8) לולאה על פני טווח של משרעת זרם. (9) הגדרת שיטה לאוטומציה של סימולציות FEM. (10) הרצת הסימולציות בשפת תכנות למטרות כלליות. אנא לחץ כאן כדי להוריד קובץ זה.
Discussion
במאמר זה הדגמנו תהליך עבודה של מידול ששילב מודלים של יסודות סופיים ונוירונים ביופיזיים. המודל גמיש מאוד, שכן ניתן לשנות אותו במורכבותו כך שיתאים למטרות שונות, והוא מספק דרך לאמת את התוצאות מול ממצאים אמפיריים. הדגמנו גם כיצד ביצענו פרמטרים של המודל כדי לאפשר אוטומציה.
שיטת המידול הדו-שלבי משלבת את היתרונות של שימוש ב-FEM ובחבילת חישובים של נוירונים כדי לפתור את משוואת הכבלים של הנוירון בנוכחות גירוי חוץ-תאי. FEM שימושי בחישוב מדויק של השדה החוץ-תאי על פני מוליך הנפח, שלעתים קרובות אינו מעשי לפתרון אנליטי במקרה של גיאומטריה מורכבת או אי-הומוגניות של מוליכות. העלות החישובית של מודל זה היא גם נמוכה יחסית, כמו תנאי סטטי הוא הניח.
בעוד ששיטת המידול המתוארת היא יתרון בקלות השימוש והגמישות שלה, ישנן מגבלות לזרימת עבודה זו של מידול. ראשית, שיטה זו לא אפשרה נוכחות של קרום עצבי בחישוב השדה החשמלי. Joucla et al.25 השוו את השיטה הדו-שלבית לשיטת FEM כולה, שבה הגיאומטריה העצבית ותכונות הממברנה נכללו במודל FEM. הם הראו כי הכללת תא העצב בחישוב השדה החשמלי תשנה את חישוב הפוטנציאל הטרנס-ממברני כאשר מבנה תא גדול יותר, כגון גוף התא, ייכלל בגאומטריה. באופן ספציפי, פישוט הגיאומטריה של הנוירונים בשיטה הדו-שלבית פירושו שפוטנציאל הטרנסממברנה של כל נקודה בתא מיוצג על ידי פוטנציאל הטרנסממברנה בצומת או בנקודת המרכז של התא. לעומת זאת, מודל ה-FEM השלם שהציע ז'וקלה כלל ייצוג מפורש של הגיאומטריה התלת-ממדית של תא העצב, מה שאפשר הערכה פרטנית של פוטנציאל הטרנס-ממברנה בכל נקודה בתוך התא. לפיכך, מודל ה- WHOLE-FEM עשוי להיות מתאים יותר אם יש צורך בצורה ובמיקום המדויקים של פוטנציאל הטרנס-ממברנה. עם זאת, שיטה זו יקרה יותר מבחינה חישובית מהשיטה הדו-שלבית.
המגבלה השנייה של שיטת המידול נוגעת לזמינות של מורפולוגיה ונתוני קינטיקה של יונים. המודל שבו נעשה שימוש כאן התבסס על נתוני הסלמנדרה הטיגריסית, ששימשו למידול RGCs ממינים אחרים, אך ייתכן שהיו הבדלים בסוגי תעלות היונים הקיימות שלא הובהרו. לפיכך, ייתכן שיהיה צורך במקרים מסוימים לבצע עבודות במבחנה כדי להתאים את הפרמטרים של ערוץ היונים.
שלישית, העלות של תוכנת FEM עשויה להיות אילוץ. במקרה זה, תוכנית FEM26 בקוד פתוח הכוללת פותר משוואות פואסון מובנה עשויה להיות חלופה. מלבד תוכנת FEM שבה נעשה שימוש, התוכנה המשמשת בתהליך עבודה זה היא בחינם. בעוד שתוכנת FEM המשמשת מציעה ממשק משתמש גרפי אינטואיטיבי ומידול זרם חשמלי מוכן לשימוש, ניתן לבצע את חישובי הערך החוץ-תאי בתוכנת תכנות למטרות כלליות. עם זאת, הדבר יחייב הגדרה ידנית של המשוואות הפיזיקליות והשיטות הנומריות לפתרון המשוואות27. יתר על כן, שיטה זו עשויה להיות מייגעת כאשר יש להשתמש בגיאומטריה מורכבת של רקמה או מערך אלקטרודות.
Disclosures
המחברים מצהירים שאין אינטרסים מתחרים.
Acknowledgements
מחקר זה ממומן על ידי מענק פרויקט המועצה הלאומית לבריאות ומחקר רפואי (מענק מספר 1109056).
Materials
| Name | Company | Catalog Number | Comments |
| Computer workstation | N/A | N/A | Windows 64-bit operating system, at least 4GB of RAM, at least 3 GB of disk space |
| Anaconda Python | Anaconda Inc. | Version 3.9 | The open source Individual Edition containing Python 3.9 and preinstalled packages to perform data manipulation, as well as Spyder Integrated Development Environment. It could be used to control the simulation, as well as to display and analyse the simulation data. |
| COMSOL Multiphysics | COMSOL | Version 5.6 | The simulation suite to perform finite element modelling. The licence for the AC/DC module should be purchased. The Application Builder capability should be included in the licence to follow the automation tutorial. |
| NEURON | NEURON | Version 8.0 | A freely-distributed software to perform the computation of neuronal cells and/or neural networks. |
References
- Greenberg, R. J., Velte, T. J., Humayun, M. S., Scarlatis, G. N., de Juan, E. A computational model of electrical stimulation of the retinal ganglion cell. IEEE Transactions on Bio-medical Engineering. 46 (5), 505-514 (1999).
- Guo, T., et al. Mediating retinal ganglion cell spike rates using high-frequency electrical stimulation. Frontiers in Neuroscience. 13, 413 (2019).
- Loizos, K., et al. Increasing electrical stimulation efficacy in degenerated retina: Stimulus waveform design in a multiscale computational model. IEEE Transactions on Neural Systems and Rehabilitation Engineering. 26 (6), 1111-1120 (2018).
- Cao, X., Sui, X., Lyu, Q., Li, L., Chai, X. Effects of different three-dimensional electrodes on epiretinal electrical stimulation by modeling analysis. Journal of Neuroengineering and Rehabilitation. 12 (1), 73 (2015).
- Wilke, R. G. H., Moghadam, G. K., Lovell, N. H., Suaning, G. J., Dokos, S. Electric crosstalk impairs spatial resolution of multi-electrode arrays in retinal implants. Journal of Neural Engineering. 8 (4), 046016 (2011).
- AC/DC module user's guide. COMSOL AB Available from: https://doc.comsol.com/5.4/doc/com.comsol.help.acdc/ACDCModuleUsersGuide.pdf (2018)
- Malmivuo, P., Malmivuo, J., Plonsey, R. . Bioelectromagnetism: Principles and Applications of Bioelectric and Biomagnetic Fields. , (1995).
- Rall, W. Electrophysiology of a dendritic neuron model. Biophysical Journal. 2, 145-167 (1962).
- Carnevale, N. T., Hines, M. L. . The Neuron Book. , (2006).
- Rattay, F. The basic mechanism for the electrical stimulation of the nervous system. Neuroscience. 89 (2), 335-346 (1999).
- Hodgkin, A. L., Huxley, A. F. A quantitative description of membrane current and its application to conduction and excitation in nerve. The Journal of Physiology. 117 (4), 500-544 (1952).
- Liang, T., et al. Threshold suprachoroidal-transretinal stimulation current required by different-size electrodes in rabbit eyes. Ophthalmic Research. 45 (3), 113-121 (2011).
- Jensen, R. J., Rizzo, J. F., Ziv, O. R., Grumet, A., Wyatt, J. Thresholds for activation of rabbit retinal ganglion cells with an ultrafine, extracellular microelectrode. Investigative Ophthalmology and Visual Science. 44 (8), 3533-3543 (2003).
- Kim, W., Choi, M., Kim, S. -. W. The normative retinal and choroidal thicknesses of the rabbit as revealed by spectral domain optical coherence tomography. Journal of the Korean Ophthalmological Society. 62 (3), 354-361 (2021).
- Guo, T., et al. Influence of cell morphology in a computational model of ON and OFF retinal ganglion cells. 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). 2013, 4553-4556 (2013).
- Haberbosch, L., et al. Safety aspects, tolerability and modeling of retinofugal alternating current stimulation. Frontiers in Neuroscience. 13, 783 (2019).
- Sheasby, B. W., Fohlmeister, J. F. Impulse encoding across the dendritic morphologies of retinal ganglion cells. Journal of Neurophysiology. 81 (4), 1685-1698 (1999).
- Rockhill, R. L., Daly, F. J., MacNeil, M. A., Brown, S. P., Masland, R. H. The diversity of ganglion cells in a mammalian retina. Journal of Neuroscience. 22 (9), 3831-3843 (2002).
- Lukasiewicz, P., Werblin, F. A slowly inactivating potassium current truncates spike activity in ganglion cells of the tiger salamander retina. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience. 8 (12), 4470-4481 (1988).
- Van Rossum, G. . Python Reference Manual. , (1995).
- . Welcome to Spyder's Documentation - Spyder 5 documentation Available from: https://docs.spyder-idle.org/current/index.html (2022)
- Rattay, F. Ways to approximate current-distance relations for electrically stimulated fibers. Journal of Theoretical Biology. 125 (3), 339-349 (1987).
- Tsai, D., Morley, J. W., Suaning, G. J., Lovell, N. H. Direct activation and temporal response properties of rabbit retinal ganglion cells following subretinal stimulation. Journal of Neurophysiology. 102 (5), 2982-2993 (2009).
- Tsai, D., Morley, J. W., Suaning, G. J., Lovell, N. H. Frequency-dependent reduction of voltage-gated sodium current modulates retinal ganglion cell response rate to electrical stimulation. Journal of Neural Engineering. 8 (6), 066007 (2011).
- Joucla, S., Glière, A., Yvert, B. Current approaches to model extracellular electrical neural microstimulation. Frontiers in Computational Neuroscience. 8, 13 (2014).
- . OpenFOAM Available from: https://www.openfoam.com/ (2022)
- Barba, L., Forsyth, G. CFD Python: The 12 steps to Navier-Stokes equations. Journal of Open Source Education. 1 (9), 21 (2018).
Reprints and Permissions
Request permission to reuse the text or figures of this JoVE article
Request PermissionExplore More Articles
This article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. All rights reserved