Fluxo monofásico e bifásico em um reator de leito compactado
Visão Geral
Fonte: Kerry M. Dooley e Michael G. Benton, Departamento de Engenharia Química, Louisiana State University, Baton Rouge, LA
O objetivo deste experimento é determinar a magnitude da má distribuição em reatores típicos de cama embalados no fluxo de fase única e duas fases (gás-líquido) e avaliar os efeitos dessa má distribuição na queda de pressão. Os conceitos de distribuição e dispersão do tempo de residência são introduzidos através do uso de rastreadores, e esses conceitos estão relacionados à má distribuição física.
A canalização em um fluxo de fase única pode ocorrer ao longo das paredes ou por fluxo preferencial através de uma porção maior da seção transversal do leito. A canalização em fluxo de duas fases pode resultar de causas ainda mais complexas, e teorias simples de fluxo de duas fases raramente prevêem quedas de pressão em camas lotadas. Um objetivo de design é sempre minimizar a extensão da canalização, encontrando os diâmetros ideais de cama e partículas para as taxas de fluxo de design e embalando uma cama de forma a minimizar o assentamento. É sempre importante quantificar quanta má distribuição pode ocorrer e projetar demais a unidade para explicar sua ocorrência.
O aparelho permeímetro mede a queda de pressão, ΔP, e a concentração de tracer (corante) saindo de camas horizontais embaladas de vidro blindado para água, ar ou fluxo de duas fases (Figuras 1 e 2). A água entra através de uma válvula de controle e pode ser roteada através de válvulas manuais para qualquer uma das cinco camas (48" de comprimento, 3" I.D.) com embalagens de vidro de tamanho diferente despejadas (aleatórias). A queda de pressão é medida usando um transmissor de pressão. O fluxo de água é medido por um transmissor de pressão diferencial (DP, orifício) e o fluxo de ar por um medidor de teste seco (semelhante a um medidor de gás doméstico). A amostra de corante é injetada rio acima por uma válvula de amostragem automatizada. A concentração de saída do corante de uma cama é medida usando um espectrômetro UV-Vis. As distribuições de tempo de residência são calculadas a partir dos testes e comparadas com as previsões de teorias sobre dispersão em leitos embalados. O fluxo de duas fases será estudado na cama 5, que contém as maiores partículas.

Figura 1: Diagrama de processo e instrumentação do aparelho.
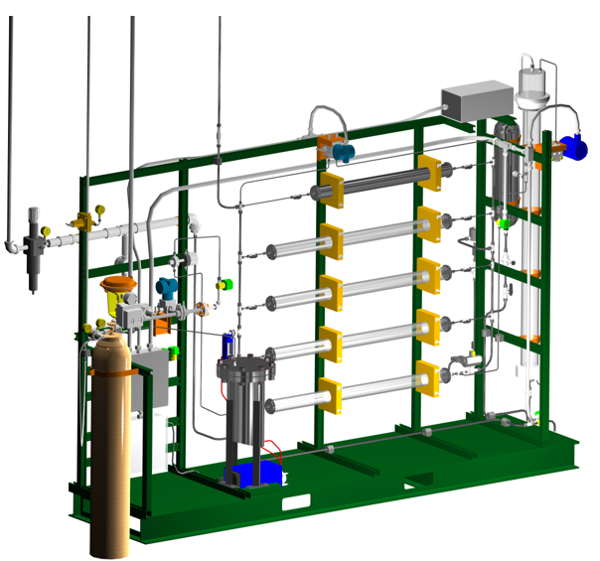
Figura 2. Renderização em 3D do aparelho. A #1 de cama está no topo, #5 na parte inferior. A válvula de controle de água está à esquerda (capô vermelho). O transmissor DP está no centro superior (azul).
Princípios
Camas embaladas verticais contracorrentes a gás -líquida (colunas embaladas) são frequentemente utilizadas em processos de separação, como destilação, absorção e descascamento. 1 Camas horizontais cocorrentes são frequentemente usadas como reatores ou adsorbers com um catalisador sólido ou adsorbent. Em ambos os casos (como separadores ou reatores), a embalagem aumenta a área superficial de contato vapor-líquido. 1 A embalagem pode existir em duas formas: embalagem descartada, consistindo em formas geométricas aleatórias ou simples de materiais como argilas, metais ou óxidos cerâmicos, ou embalagem estruturada de metais e plásticos comuns, consistindo de redes geométricas interconectadas altamente definidas (geralmente metais ondulados ou plásticos) que podem reduzir a queda de pressão em comparação com a maioria das embalagens despejadas. 1 No entanto, se horizontal ou vertical, a má distribuição (canalização) pode degradar o desempenho do separador, reator ou adsorber; às vezes, vários tipos de distribuidores de fluxo podem ser empregados para mitigar os efeitos. 2 A cama embalada de fase única ΔP's pode ser comparada com as previsões da equação de Ergun. 3
Rastreadores são corantes que são injetados instantaneamente no fluxo a montante, e cuja composição em função do tempo é medida no fluxo rio abaixo de uma cama. 4 As moléculas de rastreadores mensuráveis são consideradas características de todas as moléculas que compõem o fluxo líquido. O volume do rastreador injetado deve ser pequeno em relação ao volume do sistema. Se o fluxo de plug-flow perfeito (sem mistura axial) ocorrer em uma cama embalada, então o rastreador injetado no momento zero sairia da cama mais tarde como um pico. Para qualquer cama de verdade, o rastreador dispersará a saída do reator em concentrações mais baixas por um período maior de tempo. Se o fluxo não for maldistribuído, o espalhamento será descrito pela distribuição gaussiana (Normal), com o pico da curva observado no tempo médio de residência. Quanto mais o rastreador se espalha no tempo, pior será a má distribuição e, tipicamente, mais pobre é o processo de separação ou reação.
A distribuição de tempo de residência (RTD) descreve a distribuição de tempos que as moléculas podem passar no leito. Se M é a massa total de rastreador injetado no sistema, Q a taxa de fluxo volumoso, e C(t) é a concentração de efluentes, então o equilíbrio de massa no rastreador é:
 (1)
(1)
O lado esquerdo da Equação (1) representa a massa do rastreador dentro, e o lado direito representa massa para fora. E(t) é a distribuição de tempo de residência de saída de cama (RTD), uma distribuição de probabilidade. Usando a Equação 1 para a integral, E(t) pode ser calculado como:
 (2)
(2)
E(t)dt é a fração (probabilidade) de moléculas no fluxo de saída do tempo de residência entre t e t+dt. Os termos E-curve e RTD são sinônimos. Para camas embaladas, o tempo de residência está relacionado ao volume vazio (produto do volume total do reator V e porosidade ) dividido pela taxa de fluxo volumoso, Q. O tempo médio de residência,  , pode ser definido e relacionado a E(t)dt, a probabilidade de uma determinada molécula entrar no leito em t = 0 sairá em t:
, pode ser definido e relacionado a E(t)dt, a probabilidade de uma determinada molécula entrar no leito em t = 0 sairá em t:
 (3)
(3)
Como visto na Equação 3, E(t) tem unidades de tempo inverso. Às vezes, a curva E sem dimensão é plotada em vez da curva E. Esta curva E sem dimensão, E(t/  ), é obtida multiplicando a curva E por
), é obtida multiplicando a curva E por  . Sua média é de 1. Outra boa maneira de quantificar o desvio do fluxo de plugue (a "dispersão") é calcular a variância da curva E (σ2) dividida por sua média ao quadrado:
. Sua média é de 1. Outra boa maneira de quantificar o desvio do fluxo de plugue (a "dispersão") é calcular a variância da curva E (σ2) dividida por sua média ao quadrado:
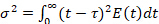 (4)
(4)
Essa quantidade deve ser invariante em relação à taxa de fluxo para uma cama embalada, se a má distribuição não estiver presente. A gama de valores devido à difusão molecular só deve ser:
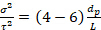 (5)
(5)
para Rep < 40, onde Rep é o número de partículas Reynolds, dp o diâmetro médio da partícula e comprimento do leito L. Valores maiores de σexperimentais 2 do que o previsto pela Equação 5 e desvios da distribuição gaussiana indicam má distribuição de fluxo, assim como um pico "precoce" na curva E(t), ou uma cauda longa no pico principal.
Em alguns casos, a natureza e a magnitude da má distribuição podem ser observadas visualmente. Isso é especialmente verdade no fluxo de duas fases. Existem dois modelos simples para o fluxo de duas fases, o modelo homogêneo e o modelo estratificado. 3,5 Para o fluxo homogêneo, as premissas básicas são de que a velocidade real do gás, UG, velocidade líquida real, UL e velocidade média da mistura líquido-gás, Utp são iguais:
UL = UG = Utp (6)
Em seguida, a densidade de duas fases é dada por G/Utp (G é velocidade de massa), e a viscosidade média de duas fases, μtp,é dada por:
μtp-1 = μL-1 (1 - X) + μG-1 X (7)
onde X é a qualidade (fração de peso de vapor em uma mistura vapor-líquido) e μL, μG são as viscosidades das respectivas fases líquidas e gasosas.
Para o fluxo estratificado, uma vez que a queda de pressão, a porosidade total e ambas as taxas de fluxo volumoso são conhecidas, a fração de volume de gás no fluxo ativo (ou seja, não estagnado), α, pode ser calculada definindo as equações de Ergun (ou equações semelhantes para ΔP) iguais para ambas as fases. Pode-se então prever ΔP/L. Não importa o tipo de fluxo, ambas as fases devem ter quedas de pressão iguais porque estão em paralelo. O equilíbrio de massa relaciona a velocidade de duas fases às velocidades de fase reais:
Utp = UL (1 - α) + UG (α) = G [ (1 - X)/ρL + X/ρG] (8)
O efeito do fluxo de gás no líquido é tanto para reduzir sua área transversal eficaz quanto para fornecer uma interface quase zero-cisalhamento. O efeito do fluxo líquido sobre o gás também é reduzir sua área transversal eficaz. Portanto, as gotas reais de pressão de fluxo de duas fases normalmente excedem as calculadas por ΔP simplesmente com base na medição ou cálculo de α e na aplicação de uma equação ΔP de cama embalada (usando α em vez de ε).
Procedimento
1. Iniciando o aparelho
O aparelho é operado principalmente através da interface do sistema de controle distribuído. Um esquema perm P&ID aparece e as válvulas automatizadas de abertura/fechamento são pontos e cliques.
- Para estabelecer o fluxo de água para #4 ou #5, abra as válvulas de entrada e saída para o leito que está sendo testado e o solenoide de abastecimento de água.
- Use o controlador de fluxo para iniciar a água que flui através da cama, levantando-a gradualmente. Bons pontos de partida são 400 mL/min para #4 de cama e 500 mL/min para #5 de cama. Monitore a pressão diferencial através das camas. Varie o fluxo para cobrir toda a faixa possível do transmissor DP.
- Ligue o equipamento espectrômetro e estabeleça comunicação com o console de controle. Os procedimentos do espectrômetro estão detalhados no manual de operação (SpectraSuite). Será fornecida a calibração do espectrômetro para as normas de corante fluorescentes.
- Realize um teste de rastreador cada um em camas #4 e 5 usando 50 ppm de corante em água DI como rastreador, a uma única taxa média de fluxo para cada cama.
- Insira a sonda espectrômetro no ponto de amostra da sonda (Fig. 1). Na interface PERM, altere o status da válvula de injeção de "Running" para "Charging".
- Injete o rastreador usando a seringa fornecida na válvula de amostra. Mude o status para "Running".
- Limpe a câmara de injeção da válvula de amostra alterando seu status de volta para "Carregar", desconectando e carregando a seringa com água, em seguida, injetando pelo menos 100 mL de água na válvula. Quando a amostra injetada tiver saído completamente do leito (a absorção de espectrômetros retorna à linha de base), mude o estado da válvula de volta para "Running" e deixe a água fluir através da válvula por 10 - 15 min a uma alta taxa de fluxo antes de usá-la novamente.
2. Realização de experimentos de queda de pressão de fluxo de duas fases
Certifique-se de que as válvulas de água para os leitos estão fechadas, as válvulas de entrada e saída para o leito #5 estão abertas, a válvula de drenagem está aberta e que a válvula manual para o ar para as camas está fechada.
- Abra lentamente o regulador de ar para estabelecer um fluxo de ar (< 5 psig no início). Abra a válvula manual para o ar para as camas.
- Ajuste o controlador de fluxo de água no ponto de ajuste desejado (700 mL/min) e a válvula manual aberta. Rote o fluxo de água/ar para o separador líquido a gás (ver valorização em Fig. 1).
- Confirme se a água está saindo para drenar. Feche a válvula para o ralo por um período de tempo para construir uma cabeça líquida no separador gás-líquido. Isso resultará em uma melhor separação do ar e da água.
- Ajuste o fluxo de ar (tipicamente < 2 SCFM) conforme desejado usando o regulador de pressão e o medidor de teste seco na linha de saída do gás. Feche a válvula de drenagem por curtos períodos de tempo para obter uma leitura correta do fluxo de gás no medidor de teste molhado.
- Realizar experimentos de queda de pressão de fluxo de duas fases (use transmissor DP) usando #5 de cama, a múltiplas taxas de ar. Tente cobrir o alcance do transmissor DP. Desconecte o medidor de teste seco se você vir a água saindo da linha de saída do gás.
Resultados
Obtenha os RTDs (E-curves, usando equações 1-2) depois de subtrair uma linha de base apropriada (se necessário) dos sinais do espectrômetro. Um exemplo de correção de linha de base para #3 de cama (não utilizado aqui) está na Figura 3. Usando equações 1-3, calcule a porosidade média, massa rastreadora, tempo médio de residência, variância e variância divididas por média ao quadrado dos RTDs. Compare a massa do rastreador calculado com massa injetada - se eles não estiverem dentro da precisão esperada, examine como a linha de base foi determinada nas medições do espectrômetro (e talvez determinar diferente). Examinar como a variância se compara à previsão da teoria da dispersão (Equações 4-5); desvios denotam canalização excessiva.
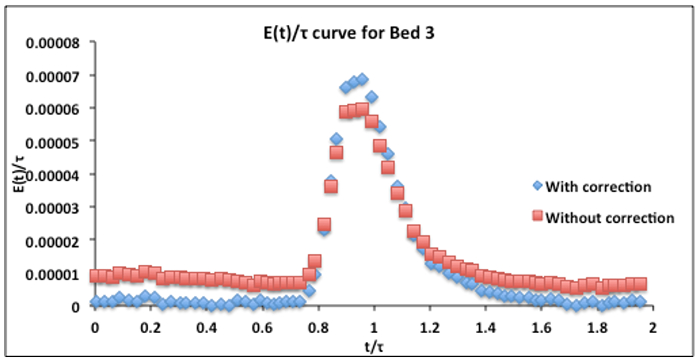
Figura 3. A cama #3 curva RTD E sem dimensão (injeção de rastreador de 390 mL/min, 50 ppm) com e sem correção da linha de base. O calculado  das Equações 2 e 3 foi de 3,6 min. A correção da linha de base foi feita subtraindo dois valores médios de linha de base, um antes e outro após o máximo. O anterior foi subtraído de todos os valores anteriores ao máximo, o outro depois foi subtraído de todos os valores após o máximo.
das Equações 2 e 3 foi de 3,6 min. A correção da linha de base foi feita subtraindo dois valores médios de linha de base, um antes e outro após o máximo. O anterior foi subtraído de todos os valores anteriores ao máximo, o outro depois foi subtraído de todos os valores após o máximo.
Uma vez encontradas as porosidades dos leitos (Equação 3), a equação de Ergun pode ser usada para prever os ΔP's para os experimentos de fluxo de água. O diâmetro médio da partícula deve primeiro ser calculado. Como o arrasto de partículas está relacionado à área de fluxo, a ponderação da superfície (d2) é geralmente a melhor maneira de obter o diâmetro médio para uma gama de partículas. O diâmetro médio pode ser computado da seguinte forma, obtendo os diâmetros das partículas a partir das informações na Lista de Materiais (ωi é a fração wt de partículas de diâmetro di):
 (9)
(9)
As porosidades calculadas podem ser usadas para identificar a causa de quaisquer discrepâncias entre preditos (pela equação de Ergun) e ΔP's medidos. Por exemplo, a porosidade mínima para esferas fechadas é de 0,36. É improvável que qualquer ε real de uma cama inteira seja menor que 0,3. Previsão ΔP's >> ΔP real sugere canalização (curto-circuito) ao longo das paredes ou na parte superior da cama quando ocorre a resolução. Tais fenômenos resultariam em um baixo ε calculado a partir da curva E, levando a ΔP's elevados previstos. É o caso da Figura 4 para ambos os leitos #3 e 4. Note-se que o ε mais esperado = 0,36 reproduziu os resultados da equação de Ergun, exceto a uma taxa de fluxo muito alta, onde uma alta porcentagem do fluxo foi através de regiões de baixa nulidade. Essa canalização pode ser realmente observada no experimento.
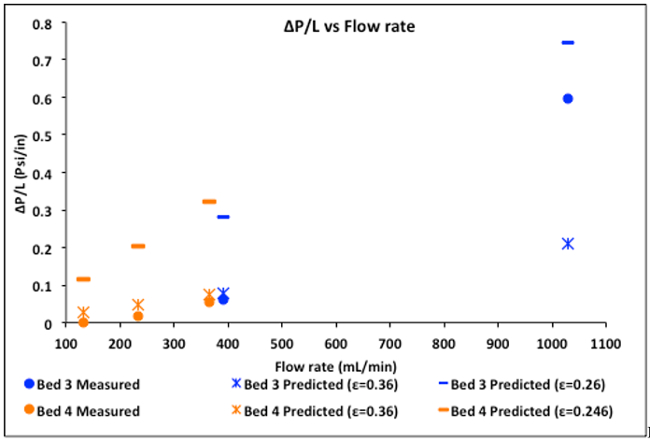
Figura 4. Δ P experimentais em comparação com as previsões da equação de Ergun, ambas em ε = 0,36 e os valores ε determinados a partir das curvas E.
Previsão ΔP's << ΔP real sugere canalizar apenas através da metade inferior da cama, ou bloqueio parcial da cama. Para essas camas, isso é improvável.
Para os fluxos de duas fases, a computação previu ΔP's tanto por fluxo homogêneo quanto teorias de fluxo estratificada usando Equações 6-9. Para o fluxo estratificado, deve-se resolver a equação de Ergun e a Equação 9 simultaneamente para obter α, definindo Ergun ΔP/L (líquido) = Ergun ΔP/L (gás). Em seguida, compare computado vs. ΔP real e veja qual teoria se aplica melhor, ou se de fato qualquer teoria se aplica. Outros regimes de fluxo (por exemplo, slug, névoa ou fluxos borbulhantes inhomogêneos) são possíveis, assim como grandes distorções de fluxo devido à canalização, que muitas vezes é mais prevalente em fluxos de duas fases.
Para fluxos de duas fases através de #5 de cama, o ΔP calculado usando a teoria do fluxo homogêneo prova ser melhor do que aqueles que usam a teoria do fluxo estratificado (Tabela 1), embora como visto nenhuma teoria se aplica exatamente. Os ΔP's reais sugerem canalização severa em uma cama horizontal durante o fluxo de duas fases - o líquido está confinado a uma pequena porção da área transversal. De fato, as frações de volume de gás estimadas pela inspeção visual pareciam ser de pelo menos 0,90. O líquido também foi confinado à região não-parede de menor vazio, o que aumenta ΔP. Os resultados refletem as limitações dos modelos reológicos mais simples para o fluxo bidárido, e por que modelos microrrehelógicos muito mais sofisticados estão encontrando mais uso hoje.
Tabela 1: Frações de volume de gás α e quedas de pressão no fluxo de duas fases, #5 de cama.
| Q água | Q ar | Q ar | α (estratificado) |
ΔDP (estratificado) Psi |
ΔDP (homogêneo) Psi |
ΔDP (real) Psi |
| mL/min | ft3/min | mL/min | ||||
| 1100 | 1.62 | 45900 | 0.58 | 2.2 | 12 | 17 |
| 1100 | 1.26 | 35700 | 0.47 | 1.7 | 10 | 14 |
| 1100 | 1.11 | 31400 | 0.38 | 1.5 | 9.5 | 11 |
| 1100 | 0.930 | 26300 | 0.19 | 1.3 | 8.6 | 8 |
| 500 | 0.73 | 20700 | 0.58 | 0.66 | 3.4 | 12 |
| 500 | 0.50 | 14200 | 0.47 | 0.50 | 2.7 | 9 |
| 500 | 0.39 | 11000 | 0.38 | 0.40 | 2.7 | 6 |
| 500 | 0.16 | 4250 | 0.19 | 0.29 | 1.4 | 3 |
Aplicação e Resumo
Neste experimento, o comportamento real de fluxo de camas horizontais embaladas, tanto em fluxo único quanto em duas fases, contrastou com os modelos teóricos mais simples para queda de pressão e dispersão (fluxo se espalhando na direção axial, desviando-se do fluxo de plugue). A utilidade dos testes de rastreadores na sondagem para má distribuição ("canalização") em tais leitos foi demonstrada, e até foi demonstrado que certas métricas calculadas a partir dos testes rastreadores podem dar alguma ideia da causa da canalização. Esses cálculos utilizando os testes de rastreador, como calcular a curva E, são normalmente conhecidos como teoria da "distribuição do tempo de residência" (RTD).
A canalização em fluxo monárco pode ocorrer ao longo de paredes ou qualquer outra região de baixa vazio, por exemplo, se a fixação ocorrer em um leito horizontal. A canalização em fluxo de duas fases pode resultar de causas ainda mais complexas, e como visto teorias simples de fluxo de duas fases raramente prevêem quedas de pressão em camas lotadas. Canalização aumenta os custos de separação a jusante ou pode arruinar o produto. Um objetivo do design é sempre minimizar a extensão da canalização, encontrando os diâmetros ideais de cama e partículas para um Q dado desejado, e embalando uma cama de forma a minimizar o assentamento.
O método de teste do rastreador é uma maneira simples de quantificar o RTD. No entanto, os rastreadores raramente são as mesmas moléculas usadas no processo (embora possam estar perto, se os isótopos forem usados). Portanto, as moléculas rastreadoras podem não se comportar exatamente da mesma maneira que moléculas reagentes ou adsorbadoras na fase do fluido. Em particular, é importante que o rastreador não adsorb nas partículas sólidas, porque então não pode ser totalmente característico de uma molécula fluida.
O tempo que cada molécula de um reagente passa dentro de um reator químico é um importante determinante da conversão macroscópica e seletividade para o produto desejado. A ocorrência de "zonas mortas" (regiões de fluxo estagnado) muitas vezes levam a seleções mais pobres do que o esperado, mesmo quando as conversões não são muito afetadas. Esta é uma das razões pelas quais a teoria do RTD é tão importante no design do reator. 4
Os rastreadores também são usados por engenheiros ambientais e de petróleo para ajudar a caracterizar a estrutura de embalagem sólida subsuperficial. Nessas aplicações, dois poços são perfurados a alguma distância; um rastreador é injetado em um e recuperado no outro. Como a subsuperfície da Terra é altamente heterogênea, os perfis de efluentes (curvas E) são tipicamente não simétricos, indicando a presença de caminhos de fluxo preferencial. Essas informações ajudam a caracterizar a estrutura dos estratos subsuperficial, que é importante para a modelagem da recuperação de petróleo e do transporte de contaminantes em águas subterrâneas.
Na engenharia ambiental, o uso de rastreadores particionários pode ser usado para localizar e quantificar contaminantes orgânicos em estratos subsuperfitos. Um rastreador inerte é injetado para caracterizar a fase fluindo (aquosa) entre dois poços. Um rastreador particionador é então injetado, particionando preferencialmente em uma fase de contaminante orgânico se existir. O rastreador é leve o suficiente para que eventualmente se difunda para fora da fase orgânica. Esse comportamento se manifesta como um atraso de tempo em relação ao rastreador inerte, e a comparação desses dois pode ser usada para deduzir o volume de fase orgânica estagnada presente.
Fluxos de duas fases também são comumente encontrados em usinas, em aplicações não-reator, não adsorber. Um exemplo é a transferência de calor fervente, com o vapor criado em uma caldeira. Eles também são encontrados em todas as colunas de destilação, absorventes e strippers, embora em configuração vertical e não horizontal.
Lista de Materiais
| Nome | Companhia | Número do catálogo | Comentários |
| Equipamento | |||
| #3 de cama - contas de vidro | Grainger | 25-40 malha (50%)
Malha 60-120 (50%) |
Embalado em paralelo |
| #4 de cama – contas de vidro e areia de explosão | Grainger | 60-120 malha (90%) - vidro
80-120 malha (6%) - vidro 120-200 malha (4%) - areia |
Misturados |
| #5 de cama – contas de vidro | Grainger | 5-10 malha | |
| Medidor de teste seco | Cantor | Modelo 803 | |
| Espectrômetro UV-Vis de fibra óptica | Óptica Oceânica | Modelo USB2000 | Inclui a fonte de luz Ocean Optics DT-1000 |
| Tubos de ensaio | VWR | 10 mL | Para calibração |
| Reagentes | |||
| Corante fluorescente amarelo/verde | Cole-Parmer | 0298-17 | Usado para compor soluções de rastreador |
Referências
- Encyclopedia of Chemical Engineering Equipment." Distillation Columns. http://encyclopedia.che.engin.umich.edu/Pages/SeparationsChemical/DistillationColumns/DistillationColumns.html. Accessed 9/22/16.
- Encyclopedia of Chemical Engineering Equipment." Absorbers. http://encyclopedia.che.engin.umich.edu/Pages/SeparationsChemical/Absorbers/Absorbers.html. Accessed 9/22/16.
- Nevers, N., Fluid Mechanics for Chemical Engineers, 3rd Ed., McGraw-Hill, 2004, Ch. 11. A derivation can be found in: M.M. Denn, "Process Fluid Mechanics", Prentice-Hall, 1980, Ch. 4.
- Fogler, H.S., "Elements of Chemical Reaction Engineering", Prentice-Hall, 2006, Ch. 13.1-13.3 and 14.3-14.4 (dispersion models); Levenspiel, O., "Chemical Reaction Engineering", 3rd Ed., John Wiley, 1999, Ch. 11 and 13 (dispersion models); Missen, R.W., Mims, C.A., and Saville, B.A., "Introduction to Chemical Reaction Engineering and Kinetics", John Wiley, 1999, Ch. 19 and 20.1.
- Levy, S., "Two Phase Flow in Complex Systems", John Wiley, 1999, Ch. 3.
Pular para...
Vídeos desta coleção:

Now Playing
Fluxo monofásico e bifásico em um reator de leito compactado
Chemical Engineering
18.9K Visualizações

Teste de eficiência da transferência de calor de um trocador de calor de tubos aletados
Chemical Engineering
17.9K Visualizações

Uso de um secador de bandeja para investigar a transferência de calor por convecção e condução
Chemical Engineering
43.9K Visualizações

Viscosidade de soluções de propilenoglicol
Chemical Engineering
32.7K Visualizações

Porosimetria de um pó de sílica alumina
Chemical Engineering
9.6K Visualizações

Demonstração do modelo de lei de potência por meio de extrusão
Chemical Engineering
10.0K Visualizações

Absorvedor de gás
Chemical Engineering
36.6K Visualizações

Equilíbrio vapor-líquido
Chemical Engineering
88.6K Visualizações

O efeito da taxa de refluxo na eficiência da destilação em bandejas
Chemical Engineering
77.6K Visualizações

Eficiência da Extração Líquido-Líquido
Chemical Engineering
48.4K Visualizações

Reator de fase líquida: Inversão de sacarose
Chemical Engineering
9.7K Visualizações

Cristalização de Ácido Salicílico via Modificação Química
Chemical Engineering
24.2K Visualizações

Cinética da Polimerização por Adição ao Polidimetilsiloxano
Chemical Engineering
16.1K Visualizações

Reator Catalítico: Hidrogenação de etileno
Chemical Engineering
30.3K Visualizações

Avaliação a Transferência de Calor de um Equipamento de Resfriamento e Agitação
Chemical Engineering
7.4K Visualizações
Copyright © 2025 MyJoVE Corporation. Todos os direitos reservados