Constantes de materiais

Fonte: Roberto Leon, Departamento de Engenharia Civil e Ambiental, Virginia Tech, Blacksburg, VA

Ao contrário da produção de carros ou torradeiras, onde milhões de cópias idênticas são feitas e testes extensivos de protótipos são possíveis, cada estrutura de engenharia civil é única e muito cara de reproduzir (Fig.1). Portanto, os engenheiros civis devem confiar extensivamente na modelagem analítica para projetar suas estruturas. Esses modelos são abstrações simplificadas da realidade e são utilizados para verificar se os critérios de desempenho, particularmente aqueles relacionados à força e rigidez, não são violados. Para realizar essa tarefa, os engenheiros necessitam de dois componentes: (a) um conjunto de teorias que explicam como as estruturas respondem às cargas, ou seja, como as forças e deformações estão relacionadas, e (b) uma série de constantes que diferenciam dentro dessas teorias como os materiais (por exemplo, aço e concreto) diferem em sua resposta.

Figura 1: World Trade Center (NYC) centro de transporte.

A maioria dos projetos de engenharia hoje em dia usa princípios lineares elásticos para calcular forças e deformações em estruturas. Na teoria da elasticidade, várias constantes materiais são necessárias para descrever a relação entre estresse e tensão. O estresse é definido como a força por unidade, enquanto a tensão é definida como a mudança de dimensão quando submetida a uma força dividida pela magnitude original dessa dimensão. As duas constantes mais comuns são o módulo de elasticidade (E), que relaciona o estresse com a cepa, e a razão de Poisson (ν), que é a razão da tensão lateral-longitudinal. Este experimento introduzirá os equipamentos típicos usados em um laboratório de materiais de construção para medir a força (ou estresse) e deformação (ou cepa), e usá-los para medir E e ν de uma barra de alumínio típica.

O modelo mais comum utilizado para análise é a elasticidade linear (Lei de Hooke), que postula que as mudanças na força (F) são diretamente proporcionais às mudanças na dimensão (Δ). Em sua forma mais simples em casos de carregamento uniaxial, força e deformação estão relacionados por uma única constante (E), ou o módulo de elasticidade:

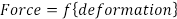(Eq. 1)

(Eq. 2)

(Eq. 3)

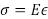(Eq. 4)

Como descrito nas equações acima, o estresse e a tensão são quantidades de engenharia, em oposição às quantidades verdadeiras. Quantidades verdadeiras requerem uma para medir as pequenas, mas finitas mudanças nas dimensões locais que ocorrem à medida que as forças são aumentadas. Experimentalmente, esse feito é muito difícil de realizar, mesmo com os recentes avanços em tecnologias de medição sem contato. Para estes cálculos, pode-se supor que essas alterações são insignificantes e usar a área original (A₀) e comprimento (L₀).

Para determinar o módulo de elasticidade das equações acima, deve-se ter uma maneira de determinar as mudanças de força e comprimento à medida que um espécime é carregado. Em um experimento bruto, pode-se usar uma balança de banheiro e uma régua para realizar essas tarefas. Primeiro, pode-se pegar um elástico espesso, medir suas dimensões, e marcar dois pontos na banda separados por uma polegada. Em seguida, pode-se colocar um recipiente aberto em uma balança e adicionar água até que a leitura seja de dez quilos. Pode-se então suspender o recipiente com o elástico e medir o quanto as duas marcas se separaram. Esta medição nos dará todos os dados necessários para calcular E para borracha, uma vez que temos todos os valores necessários para resolver para E em Eqs. (2) até (4). No entanto, haverá grandes incertezas e erros associados à medição por causa do dispositivo de medição muito bruto. Uma vez que a magnitude da tensão necessária para ser medida para materiais típicos de construção estão na ordem de 1x10^-6, dispositivos de medição muito mais precisos são necessários para determinar as constantes materiais experimentalmente. Para as aplicações de engenharia mais comuns, essas medidas são baseadas em mordaças de tensão de resistência elétrica. Como esses dispositivos serão usados ao longo dos vídeos subsequentes, uma descrição de seus princípios operacionais será dada em seguida.

Uma gagem de tensão é um fio longo em loop embutido em uma matriz portadora (Fig. 2). A gagem de tensão é colada ao material que está sendo testado com um epóxi de alta resistência. Quando o material estiver deformado, os fios mudarão de comprimento e sua resistência mudará ligeiramente como resultado. Quando a gagem é inserida como parte de um circuito de ponte de Wheatstone, essas alterações podem ser detectadas como alterações na tensão. O advento dos sistemas de medição digital reduziu consideravelmente o ruído de fundo e outras fontes de erro dentro do circuito, melhorando assim a precisão na qual as mudanças de tensão podem ser medidas hoje. A gagem de tensão é calibrada usando uma constante conhecida como fator de gagem, de modo que sua saída esteja linearmente relacionada à tensão para uma determinada faixa de tensão sob uma dada entrada de tensão.

Uma mordia de tensão mede a tensão em apenas uma direção. Para obter o estado completo de estresse em um ponto em uma superfície, é necessária uma gagem de cepa de roseta, composta por três mordaças de cepa alinhadas a 45º umas às outras (Fig. 3). Com essas medidas em três direções diferentes, todo o estado de estresse em uma superfície pode ser definido usando princípios como o círculo de Mohr para calcular cepas e tensões principais máximas e mínimas.

Figura 2: Gage de tensão.

Figura 3: Gage de cepa de roseta.

Medidas de força também são feitas com mordaças de tensão; no entanto, essas medidas são geralmente tomadas em uma configuração de ponte completa (ou seja, as resistências internas em um circuito de ponte de Wheatstone são substituídas por mordaças ativas externas) resultando em um dispositivo chamado célula de carga. A célula de carga em si é geralmente um cilindro de aço de alta resistência com duas mordaças instaladas longitudinalmente e duas instaladas transversalmente para eliminar os efeitos da razão de Poisson. A calibração de uma célula de carga requer que os pesos mortos sejam usados para que a saída de tensão do circuito possa estar relacionada a uma determinada carga. Nos Estados Unidos, o Instituto Nacional de Ciência e Tecnologia (NIST) calibra células de carga de até 5 milhões de kN usando pesos mortos e mecanismos de alavanca. Todas as células de carga usadas nos EUA devem ser rastreáveis a esta fonte de calibração. Na prática, a rastreabilidade significa que a célula de carga A é calibrada pelo NIST usando pesos mortos, levada para outros laboratórios e instalada em série com célula de carga B. Finalmente, a célula de carga B é calibrada com base na comparação de sua saída com a saída da célula de carga A. Todas as células de carga devem ser periodicamente calibradas para garantir que estejam funcionando corretamente.

Normalmente, a célula de carga é instalada em uma máquina de teste universal (UTM). Um UTM consiste em um quadro de auto-reação com duas colunas de parafusos que são viradas por um motor (Fig. 4). Ao fixar uma amostra de teste nas garras UTM e girar a coluna do parafuso de tal forma que a cabeça cruzada se move para cima, forças de tração são introduzidas no espécime. A força aplicada é medida pela célula de carga, que é instalada em série com a amostra. Por outro lado, se as placas forem instaladas em vez de apertos de tração e as colunas de parafusos forem movidas para baixo, forças compressivas são introduzidas na amostra de teste (ou seja, para testar cilindros de concreto).

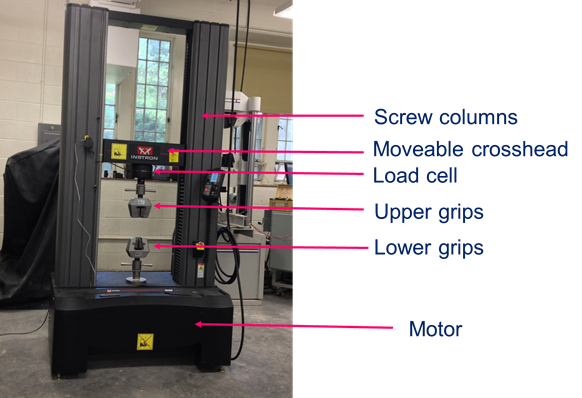
Figura 4: Máquina de teste universal.

Agora que foi demonstrado como medir a tensão e a força, um tratamento mais geral da teoria da elasticidade será discutido. Olhando para um pedaço genérico de uma estrutura submetida a cargas, pode-se escrever equações de equilíbrio para forças e momentos ao longo de todos os eixos.

Isso resulta em uma série de equações para cepas normais (ε) e tesouras (γ) da forma:

(Eq. 5)

(Eq. 6)

São necessárias seis equações deste tipo, três para cepas normais(ε_x, ε_y e ε_z) e três para cepas de tesoura(γ_xy, γ_yz e γ_zx) para estabelecer as deformações globais. Estas equações contêm três constantes materiais: o módulo de elasticidade (E), a razão de Poisson (ν) e o módulo de cisalhamento (G). Como mostrado na equação acima, o módulo de cisalhamento é a mudança na deformação angular dado um estresse de cisalhamento ou tração superficial. A razão de Poisson é definida como:

(Eq. 7)

Pode-se mostrar que:

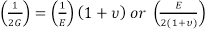= G (Eq. 8)

Assim, apenas duas das três constantes precisam ser determinadas para definir as três. Existem inúmeras outras constantes derivadas que são usadas na teoria da elasticidade, todas elas podem ser derivadas dessas medidas. Por exemplo, o módulo a granel (B), ou a alteração relativa no volume de um corpo produzido por uma unidade compressiva ou tensão de tração agindo uniformemente sobre sua superfície, é:

De Eqs. (5) e (6), pode-se determinar o estado de estresse e tensão em uma superfície se pelo menos três medidas de cepa independentes forem feitas. Se uma gagem de cepa de roseta, que tem três mordaças a 45° umas às outras (Fig. 3) é usada em vez de uma única gagem longitudinal, então pode-se encontrar as cepas principais máximas e mínimas (ε₁, ε₂) e o ângulo (Φ) entre as cepas medidas e as principais cepas do círculo de Mohr.

Para uma gagem de cepa de roseta retangular, como a mostrada na Fig. 3, onde as mordaças estão a 45 graus umas às outras:

(Eq. 9)

Φ =

A gama de cepas sobre as quais as relações elásticas lineares se mantêm está entre zero e o limite proporcional do material. Neste experimento, que usará alumínio, a gama de cepas será mantida bem abaixo desse limite.

Usaremos um simples feixe de cantilever instrumentado com mordaças de tensão para ajudar a ilustrar os conceitos de tensão principal e tensões e o cálculo do módulo de Young (E) e da razão de Poisson (ν).  O feixe cantilever será carregado incrementalmente com um conjunto de pesos e as alterações correspondentes na tensão registrada.  As tensões correspondentes podem ser calculadas a partir da simples equação de estresse de dobra:

(Eq. 11)

onde M é o momento (ou força multiplicada por seu braço de alavanca), c é a distância do centroide até a fibra extrema no feixe através de sua profundidade ( ), e eu sou o momento da inércia, dado por onde b é a largura do feixe e t é sua espessura.

Módulo de Elasticidade e Razão de Poisson

Presume-se aqui que os alunos foram treinados nas precauções de uso e segurança necessárias para operar uma máquina de teste universal.

1. Obter uma barra de alumínio retangular (12 in. x 1 in. x 1/4 in.); recomenda-se um alumínio 6061 T6xxx ou mais forte. Um orifício deve ser perfurado cerca de 1 em. de uma extremidade de feixe para servir como um ponto de carga.
2. Marque uma localização na viga cerca de 8.0 em. do centro do buraco na superfície superior do feixe. Desenhe marcas de alinhamento para as mordaças de cepa de roseta e certifique-se de que os eixos da roseta estão inclinados em um pequeno ângulo (cerca de 10° a 15°) ao eixo longitudinal do feixe.
3. Marque uma localização semelhante na superfície inferior do feixe. Uma única gagem de tensão será instalada aqui e deve ser alinhada com os eixos longitudinais do feixe.
4. Meça largura (b) e espessura(t)da barra cuidadosamente usando pinças. Realize três réplicas em três locais diferentes para obter uma boa média das dimensões. A partir dessas medidas, calcule o momento da inércia (I) e a distância do eixo neutro até a fibra extrema da barra (c=t/2).
5. Obtenha uma gagem de cepa de roseta com uma grade de detecção de aproximadamente 1/4 in. longa por 1/8 mm de largura em cada gárage e uma gagem de tensão única semelhante. Observe os fatores de calibração (ou fator de gagem) para todas as mordaças.
6. Para instalar a gagem de cepa de roseta, primeiro desengreça e limpe a superfície cuidadosamente; lixe a superfície usando lixa progressivamente mais fina até obter uma superfície muito lisa; limpar a superfície com um neutralizador; e cole a gagem da cepa de acordo com as especificações do fabricante. Deixe a cola curar corretamente antes de prosseguir.
7. Teste a resistência das mordaças (tipicamente 120 ohms) e seu vazamento atual para a barra (resistividade, idealmente maior que 5 Mohms) antes de prosseguir.
8. Repita as etapas 1.5 a 1.7 para que a gagem única seja instalada na superfície inferior.
9. Insira a amostra no aparelho cantilever e proteja adequadamente.
10. Conecte as mordaças de tensão a um dispositivo de gravação, como um indicador de tensão Vishay P3. Certifique-se de que a fiação está correta de acordo com as instruções do indicador de tensão e que você sabe qual canal corresponde a cada gagem de tensão.
11. Digite os fatores de gagem apropriados para cada gálage no indicador.
12. Verifique a calibração do dispositivo inserindo uma tensão conhecida que resultará em uma leitura de 5000με a um fator de gagem de 2,00.
13. Registo inicial de carga e tensões.
14. Aplique lentamente 9 incrementos de 0,5kg ou similares na extremidade do feixe. Faça uma pausa a cada passo e permita que as medidas se estabilizem antes de gravar as leituras.
15. Aplique lentamente 9 decréscreções de 0,5kg ou similares. Faça uma pausa a cada passo e permita que as medidas se estabilizem antes de gravar as leituras.
16. Desconecte a gagem da tensão do indicador de tensão e desligue o indicador.
17. Plote a tensão na gage longitudinal versus a tensão na gágio transversal. A inclinação desta linha corresponde à razão de Poisson, v.
18. Determine a inclinação da linha de ajuste melhor do enredo de estresse vs. tensão longitudinal, que é igual ao módulo de Young, E.
19. Compare seus valores de E e v com valores previamente estabelecidos ou publicados (em geral, haverá uma gama de valores dados em vez de um único valor discreto).

Os dados devem ser importados ou transcritos em uma planilha para fácil manipulação e grafia. Os dados coletados são mostrados na Tabela 1.

Como a gagem da cepa de roseta não está alinhada com os principais eixos do feixe, as cepas de roseta precisam ser inseridas nas equações para ε_1,2 (Eq. 9) e ε (Eq. 10) acima para calcular as cepas principais, resultando nos dados mostrados na Tabela 2. A tabela mostra que o ângulo entre o estresse medido e as tensões principais é de cerca de 0,239 radianos ou 13,7°. Note que a cepa principal máxima é positiva, correspondendo a uma grande tensão de tração longitudinalmente; a cepa principal mínima é negativa, correspondendo a uma cepa transversal menor. A razão entre as cepas mínima e máxima principal corresponde à razão de Poisson, que é mostrada na última coluna e tem média de cerca de 0,310.

	Carga	Gage 1	Gage 2	Gage 3	Gage 44
Passo	(Lbs.)	με	με	με	με
1	0.00	1	1	1	0
2	1.10	83	56	-21	-87
3	2.21	163	115	-41	-171
4	3.31	243	171	-62	-254
5	4.42	325	228	-83	-338
6	5.52	400	280	-104	-423
7	6.62	485	338	-122	-501
8	7.73	557	386	-143	-589
9	8.83	634	442	-163	-665
10	9.93	714	502	-184	-741
11	8.83	637	445	-162	-664
12	7.73	561	391	-142	-584
13	6.62	483	335	-123	-506
14	5.52	406	281	-102	-423
15	4.42	323	227	-83	-339
16	3.31	245	171	-62	-256
17	2.21	164	115	-41	-170
18	1.10	83	56	-21	-87
19	0.00	1	0	1	2

Tabela 1: Cepas na barra de alumínio.

Fator Gage	1	2	3	Tensão máxima principal	Mínimo. Tensão principal	Ângulo	Razão de Poisson
Passo de carga	με	με	με	(Eq. 9)	(Eq. 9)	(Eq. 10)	(Eq. 7)
1	1	1	1	1	1	0	0
2	83	56	-21	89	-26	-0.223	0.297
3	163	115	-41	176	-55	-0.243	0.311
4	243	171	-62	263	-82	-0.242	0.312
5	325	228	-83	351	-109	-0.240	0.311
6	400	280	-104	432	-136	-0.240	0.314
7	485	338	-122	523	-160	-0.237	0.307
8	557	386	-143	600	-186	-0.236	0.310
9	634	442	-163	684	-213	-0.238	0.312
10	714	502	-184	773	-242	-0.242	0.314
11	637	445	-162	688	-213	-0.239	0.309
12	561	391	-142	605	-186	-0.237	0.308
13	483	335	-123	520	-161	-0.236	0.309
14	406	281	-102	437	-133	-0.234	0.303
15	323	227	-83	349	-109	-0.241	0.313
16	245	171	-62	264	-81	-0.238	0.308
17	164	115	-41	177	-54	-0.239	0.302
18	83	56	-21	89	-26	-0.223	0.297
19	1	0	1	2	0	0.000	0.000
					Média	-0.239	0.310

Tabela 2: Principais cepas e ângulo de inclinação.

As cepas principais máximas e mínimas da Tabela 2 são traçadas em Fig. 5, que mostra tendências muito lineares (R² = 0,999) para a razão de Poisson. O valor obtido para a razão de Poisson (0,31), que corresponde à inclinação da linha, é muito próximo dos 0,30 dados na maioria das referências para alumínio e outros metais.

Figura 5: Principais dados de tensão que mostram a inclinação da linha entre a cepa principal máxima e mínima, que corresponde à razão de Poisson.

Uma boa interpretação física dos dados de gagem da cepa de roseta pode ser obtida com a plotagem das principais cepas em um círculo mohr (Fig. 6). Note-se que as três medidas, mostradas aqui para o caso da carga máxima de 7,4 lbs., correspondem a três pontos no círculo a 90º um ao outro, começando em um ângulo de cerca de 27,4º (ou 2Φ) no sentido anti-horário do eixo x.

Figura 6: Significado físico das leituras de roseta de cepa mostradas no círculo de Mohr para tensão.

A Tabela 3 mostra as cargas, os resultados da tensão principal da tração principal da gálada única na parte inferior do feixe (Gage 4, que está em compressão), a razão entre as tensões principais inferiores e superiores, o estresse de Eq. (11) e o módulo de Young (E) como a razão do estresse de Eq. (11) dividido pela tensão de Eq. (9). Na Tabela 3, o módulo de um Young é calculado como 10147 ksi, tomando a média do moduli calculado para as 15 etapas de carregamento intermediário.

	Carga	Max, diretor. Coar	Estresse máximo principal	Min Principal Stress	Estresse de dobra	Modulo Jovem
Passo de carga	Lbs.	με	Ksi	Ksi	Psi	Ksi
1	0.00	1	10	9	0	0
2	1.10	89	886	0	882	9945
3	2.21	176	1765	0	1763	9991
4	3.31	263	2630	0	2645	10058
5	4.42	351	3513	0	3526	10038
6	5.52	432	4324	0	4408	10195
7	6.62	523	5230	0	5290	10113
8	7.73	600	6001	0	6171	10283
9	8.83	684	6843	0	7053	10307
10	9.93	773	7726	0	7935	10269
11	8.83	688	6877	0	7053	10256
12	7.73	605	6051	0	6171	10198
13	6.62	520	5204	0	5290	10165
14	5.52	437	4368	0	4408	10091
15	4.42	349	3494	0	3526	10092
16	3.31	264	2644	0	2645	10004
17	2.21	177	1770	0	1763	9960
18	1.10	89	886	0	882	9945
19	0.00	2	19	0	0	0
					Média	10147

Tabela 3: Cálculo do módulo de elasticidade (E).

Os dados para E também são traçados na Fig. 7, o que indica uma excelente relação linear (alta R²) entre estresse e tensão e uma inclinação de cerca de 10.147 ksi. A diferença entre o módulo da Tabela 3 e o da Fig. 6 surge porque os cálculos para a inclinação em Fig. 6 exigem que a interceptação passe por zero. As magnitudes se comparam muito favoravelmente (erro inferior a 1,5%) com os valores publicados de E para alumínio 6061T6, que geralmente é dado como 10.000 ksi.

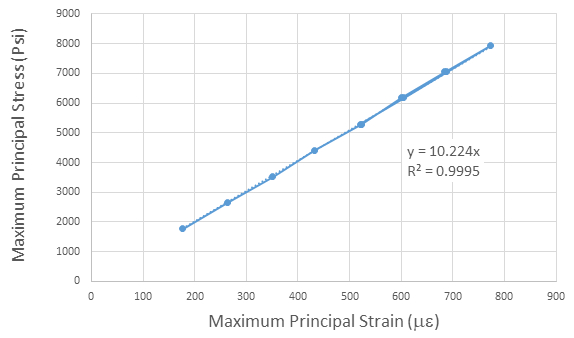
Figura 7: Inclinação da linha de tensão máxima versus tensão máxima é o módulo de Young.

Finalmente, reformulando Eqs. (5) e (6) em:

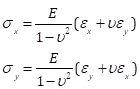(Eq. 12)

podemos calcular as principais tensões usando o círculo de Mohr. Para o caso da etapa correspondente a 6,61 lbs. de carga, as principais cepas de (634, -189) levam a tensões principais de (7,34, 0,00) ksi (Fig. 8). Embora os cálculos aqui sejam feitos utilizando as expressões para o estresse plano, os resultados indicam corretamente que ao longo do eixo principal o estresse na direção perpendicular é zero (ou muito próximo a ele), correspondente ao caso do carregamento uniaxial. Os valores de estresse em um ângulo de 2Φ = 0,40 radianos são (6,50, 2,82) ksi.

Figura 8: Círculo de Mohr para estresse de avião para o caso de uma carga de 7,34 lbs.

Neste experimento, foram medidas duas constantes materiais fundamentais: o módulo de elasticidade (E) e a razão de Poisson(v). Este experimento demonstra como medir essas constantes em um ambiente de laboratório usando uma gagem de cepa de roseta. Os valores obtidos experimentalmente correspondem bem aos valores publicados de 10.000 ksi e 0,3, respectivamente. Esses valores são fundamentais na aplicação da teoria da elasticidade para o design de engenharia, e esta técnica experimental aqui descrita são típicas daquelas utilizadas para a obtenção de constantes materiais. Para obter esses valores, deve-se ter muito cuidado tanto na utilização de procedimentos de instrumentação de alta resolução quanto de calibração rastreável. Em particular, o uso de dispositivos baseados em gagem de tensão e sistemas de aquisição de dados digitais de 16 a 24 bits são parte integrante do sucesso e qualidade desses experimentos.

Hoje, existem outros métodos de determinar o módulo de Young de um material, incluindo métodos de propagação de ondas (método ultrassônico de eco-pulso) e nanoindentação. Um benefício de utilizar a propagação de ondas é que é um dos métodos não destrutivos de medir o módulo de Young, enquanto o nanoindentation e o uso de uma gagem de cepa de roseta são métodos mais invasivos.

O design de qualquer produto de engenharia, de uma torradeira a um arranha-céus, requer o uso de modelos analíticos eficazes para melhorar e otimizar o design. A teoria da elasticidade é a base da maioria dos modelos utilizados no design de engenharia civil, e baseia-se no estabelecimento de várias constantes.

Modelos analíticos são necessários quando apenas uma única (ou muito poucas) réplicas serão construídas. Como o custo e o desempenho da estrutura dependem do resultado dessas análises, e essas análises, por sua vez, dependem de ter valores robustos para as propriedades materiais, testes como os descritos aqui devem ser executados para garantir controle de qualidade e garantia de qualidade no processo de construção. Por exemplo:

• Ao escolher uma fachada para um edifício, o arquiteto deve ter o cuidado de projetar um envelope impermeável. O aperto de água de uma fachada de construção de tijolos pode depender da manutenção da argamassa entre os tijolos descasquedos, entre outros fatores. Se a argamassa rachar, a água penetrará e causará problemas de corrosão e umidade que serão muito caros de consertar. Para determinar quanta força a argamassa pode resistir antes de rachar, precisamos de uma teoria e suas constantes associadas. O arquiteto e engenheiro estrutural deve trabalhar juntos para determinar quais cargas a fachada verá (auto-peso, vento, chuva de condução, etc.) e como cada opção de projeto irá funcionar nessas condições. Só então uma argamassa com as características apropriadas deve ser escolhida.
• Na construção de um edifício alto, como o Burj Dubai, a construtora precisa prestar muita atenção para manter o nível do piso. À medida que a construção progride, se os tamanhos das colunas e paredes forem diferentes, alguns desses elementos podem encurtar (a tensão) mais do que outros à medida que a construção progride e mais peso (estresse) é adicionado. Para obter pisos planos no final da construção, a construtora precisará fazer ajustes na altura das colunas e paredes nos andares inferiores - os andares inferiores podem não estar nivelados durante as fases iniciais de construção, mas devem ser achatados no final. Para calcular como fazer esses ajustes corretamente, a construtora contratará um engenheiro estrutural para fornecer dados sobre colunas diferenciais e alturas de parede. O engenheiro precisará usar constantes materiais para realizar esses cálculos.
• No design de uma lata de refrigerante, um fabricante deve minimizar a espessura da parede de alumínio, já que o alumínio é um material muito caro. Para otimizar a forma e as dimensões das latas, o fabricante precisa determinar quais condições de carregamento são importantes; as condições de transporte e armazenamento podem ser mais exigentes do que o consumidor beber dele. Muitas dessas condições serão difíceis e caras de serem replicantes dentro de um programa experimental de testes; o fabricante pode optar por fazer uma série de análises para otimizar as dimensões da lata antes de passar para a fase do protótipo. Este procedimento é o que a Boeing seguiu no desenvolvimento do Dreamliner (Boeing 787). Para fazer esses estudos, as propriedades materiais devem ser conhecidas e a teoria apropriada selecionada.