Teoria degli orbitali molecolari
Panoramica
Fonte: Tamara M. Powers, Dipartimento di Chimica, Texas A & M University
Questo protocollo serve da guida nella sintesi di due complessi metallici caratterizzati dal ligando 1,1'-bis(difenilfosfino)ferrocene (dppf): M(dppf)Cl2, dove M = Ni o Pd. Mentre entrambi questi complessi di metalli di transizione sono a 4 coordinate, presentano geometrie diverse al centro del metallo. Utilizzando la teoria degli orbitali molecolari (MO) in combinazione con 1H NMR e il metodo evans, determineremo la geometria di questi due composti.
Principi
Ci sono una varietà di modelli che i chimici usano per descrivere il legame nelle molecole. È importante ricordare che i modelli sono rappresentazioni di sistemi e quindi hanno punti di forza ma anche importanti limitazioni. Ad esempio, le strutture a punti di Lewis, il metodo più semplice per descrivere come gli atomi condividono gli elettroni, non tengono conto della geometria degli atomi nella molecola. La teoria vsEPR (Valence Shell Electron Pair Repulsion) descrive la geometria degli atomi, ma non fornisce una spiegazione per l'osservazione che le specie isoelettroniche con lo stesso numero di elettroni di valenza possono presentare geometrie diverse. Soprattutto per i complessi di metalli di transizione, entrambi questi modelli non sono in gradi di descrivere il legame dei metalli. La teoria dei campi cristallini è un modello di legame specifico per i complessi di metalli di transizione. Questo modello esamina gli effetti del campo elettrico di un ligando sugli orbitali atomici d o f di un centro metallico. L'interazione si traduce in una rottura nella degenerazione di quegli orbitali atomici.
In questo video, ci concentreremo sulla teoria MO, che è un modello potente che può essere utilizzato per descrivere il legame non solo nelle molecole del gruppo principale, ma è anche adatto per modellare il legame nei complessi di metalli di transizione. Qui, dimostreremo come generare un diagramma MO di composti contenenti metalli.
Teoria MO:
La teoria MO descrive il legame chimico come la combinazione lineare degli orbitali atomici (LCAO) di ciascun atomo in un dato composto. Gli MO che risultano dagli LCAO descrivono sia la geometria che l'energia degli elettroni condivisi da un numero di atomi nella molecola(cioè,la direzionalità e la forza dei legami formati da dati atomi).
Per rivedere le basi della teoria MO, si consideri prima la molecola biatomica F2 (diagramma MO completo in Figura 1). Un atomo di fluoro ha 4 orbitali atomici di valenza: 2s, 2px, 2pye 2pz. L'orbitale 2s è più basso in energia rispetto agli orbitali atomici 2p, che hanno tutti la stessa energia. Una combinazione lineare di orbitali atomici si verificherà tra orbitali atomici di energia simile e di simmetria corrispondente. In questo caso, l'orbitale 2s su un atomo F interagirà con l'orbitale 2s sull'altro atomo F. L'aggiunta di questi due orbitali provoca la formazione di un MO di legame σ (Figura 1). Il legame è un'interazione stabilizzante e, quindi, il risultante σ MO è più basso in energia rispetto all'energia degli orbitali atomici 2s. Sottraendo gli orbitali 2s si traduce in un'interazione anti-legame (destabilizzante), designata come σ*, che è più alta in energia rispetto agli orbitali atomici2 s (Figura 1).

Figura 1. Diagramma MO di F2.
Allo stesso modo, gli orbitali atomici 2p si combineranno per formare interazioni di legame e anti-legame. Come gli orbitali atomici 2s, gli orbitali atomici 2pz (che si trovano lungo il legame F-F) formano interazioni σ e σ*. Se consideriamo gli orbitali atomici 2px e 2py, vediamo che formano diversi tipi di interazioni di legame e anti-legame, chiamate rispettivamente π e π*, (Figura 1). È facile distinguere tra legami σ e π perché gli orbitali di legame σ sono cilindricamente simmetrici rispetto all'asse internucleare, mentre gli orbitali π hanno un piano nodale lungo l'asse internucleare. La sovrapposizione spaziale tra orbitali atomici che formano legami σ è maggiore della sovrapposizione spaziale tra orbitali atomici che formano legami π. Pertanto, i π e i π* MO risultanti sono rispettivamente meno stabilizzati e destabilizzati rispetto ai σ e σ* MO formati dagli orbitali atomici 2pz. Possiamo quindi riempire i MO con gli elettroni di valenza per i due atomi F.
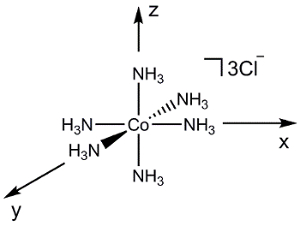
Consideriamo ora una molecola più complessa come [Co(NH3)6]Cl3 (Figura 2). Se dovessimo usare lo stesso processo di cui sopra (considerando la sovrapposizione orbitale atomica tra 2 atomi alla volta), generare un diagramma MO di questa molecola sarebbe estremamente impegnativo. Invece, possiamo usare la teoria dei gruppi per generare prima una combinazione lineare adattata alla simmetria (SALC) dei ligandi. Possiamo quindi usare la simmetria per determinare le interazioni di legame / anti-legame che si formano tra gli orbitali atomici sul metallo e le SALC risultanti.
| Oh | E | 8C3 | 6C2 | 6C4 | 3C2' | io | 6S4 | 8S6 | 3σore | 3σd | ||
| A1g | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | x2+y2+z2 | |
| A2g | 1 | 1 | -1 | -1 | 1 | 1 | -1 | 1 | 1 | -1 | ||
| Eg | 2 | -1 | 0 | 0 | 2 | 2 | 0 | -1 | 2 | 0 | (2z2-x2-y2, x2-y2) | |
| T1g | 3 | 0 | -1 | 1 | -1 | 3 | 1 | 0 | -1 | -1 | (Rx, Ry, Rz) | |
| T2g | 3 | 0 | 1 | -1 | -1 | 3 | -1 | 0 | -1 | 1 | (xz, yz, xy) | |
| A1u | 1 | 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | ||
| A2u | 1 | 1 | -1 | -1 | 1 | -1 | 1 | -1 | -1 | 1 | ||
| Eu | 2 | -1 | 0 | 0 | 2 | -2 | 0 | 1 | -2 | 0 | ||
| T1u | 3 | 0 | -1 | 1 | -1 | -3 | -1 | 0 | 1 | 1 | (x, y, z) | |
| T2u | 3 | 0 | 1 | -1 | -1 | -3 | 1 | 0 | 1 | -1 | ||
| Γrosso | 6 | 0 | 0 | 2 | 2 | 0 | 0 | 0 | 4 | 4 |
Γrosso =A1g + Eg + T1u
Figura 2. Combinazione lineare di orbitali atomici ligandi di [Co(NH3)6]Cl3.
Per generare i SALC per [Co(NH3)6]3+, seguiamo una procedura simile delineata nel video "Teoria dei gruppi" della serie chimica inorganica:
1. Determinare il gruppo di punti della molecola.
2. Generare una rappresentazione riducibile degli orbitali atomici del ligando.
3. Ridurre la rappresentazione riducibile a rappresentazioni irriducibili.
[Co(NH3)6] 3+ è nel gruppo di punti Oh. Poiché siamo preoccupati solo per il legame al centro del metallo, possiamo semplicemente considerare gli orbitali atomici2 s su ciascun ligando NH3. Se seguiamo i passaggi 1-3 per gli N 2s, orbitali troviamo che la rappresentazione riducibile è Γrosso = A1g + Eg + T1u (Figura 2). Mentre l'insieme A1g rappresenta 1 SALC, gli insiemi Eg e T1u rappresentano in realtà rispettivamente 2 e 3 SALC, per un totale di 6 SALC (lo stesso numero di ligandi nel catione [Co(NH3)6]3+). Le 2 SALC nell'insieme Eg hanno la stessa simmetria e si tradurranno in MO degenerati quando interagiscono con gli orbitali atomici del Co (lo stesso si può dire delle 3 SALC nell'insieme T1u). Usando la tabella dei caratteri in Figura 2, possiamo determinare come gli orbitali atomici di Co si trasformano nel gruppo di punti Oh. Ad esempio, gli orbitali dz2 e dx2–y2 formano un insieme Eg. Poiché abbiamo 2 SALC ligando con simmetria Eg, quelle SAC formeranno interazioni di legame / anti-legame con gli orbitali atomici dz2 e dx2-y 2 Co. Continuando allo stesso modo per tutti gli orbitali atomici di valenza di Co, generiamo un diagramma MO per il complesso dei metalli di transizione, mostrato in Figura 3. Si noti che i restantid -orbitali (dxz, dyze dxy) si trasformano come un insieme (T2g) ma non hanno una simmetria appropriata abbinata a SALC. Questi orbitali atomici diventano quindi MO "non leganti". In altre parole, non partecipano al legame con i ligandi in questo complesso di metalli di transizione.
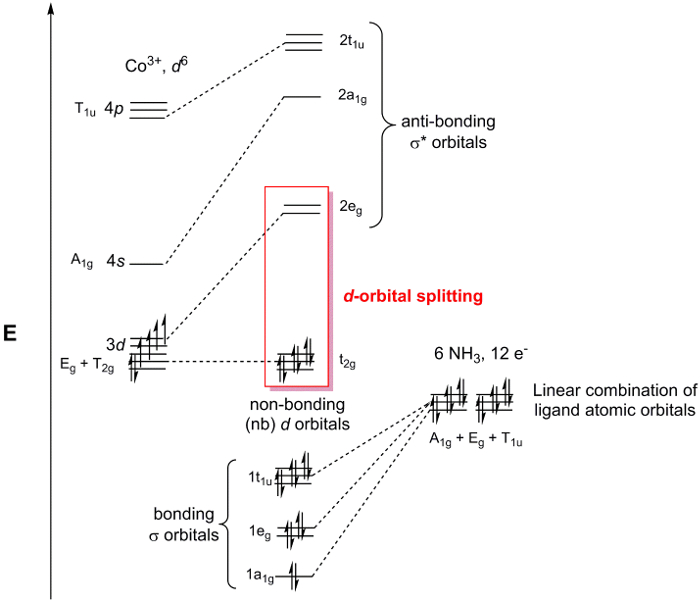
Figura 3. Diagramma MO per [Co(NH3)6]Cl3.
Nella Figura 3 sono evidenziati gli orbitali dnon leganti e gli orbitali σ* con carattere orbitale d. Quando questo gruppo di MO è considerato separatamente dall'intero diagramma MO, viene indicato come il diagramma di scissione orbitale ddi un complesso di metalli di transizione. Poiché il diagramma di scissione orbitale dcontiene l'HOMO e il LUMO, che sono in genere gli orbitali più importanti per comprendere la chimica e la spettroscopia dei complessi di coordinazione, i chimici spesso si riferiscono al diagramma di scissione orbitale dinvece dell'intero diagramma MO. Convenientemente, il diagramma di scissione orbitale dpuò essere riempito con il numero di de- sul centro del metallo, poiché gli elettroni basati sul ligando riempiono sempre gli MO basati sul σ nel diagramma MO.
Considerando i diagrammi di scissione orbitale dper M(dppf)Cl2:
Considera un semplice complesso metallico a 4 coordinate MX4. MX4 può esistere in due geometrie: tetraedrica o quadrata planare. I diagrammi di scissione orbitale dper i gruppi di punti Td (tetraedrico) e D4h (planare quadrato) sono mostrati nella Figura 4. Mentre i complessi metallici generali M(dppf)Cl2 non hanno 4 ligandi equivalenti, e quindi non sono nei gruppi puntini Td o D4h, possiamo ancora usare questi diagrammi di scissione orbitale dcome modello per descrivere gli MO orbitali dper le due possibili geometrie.
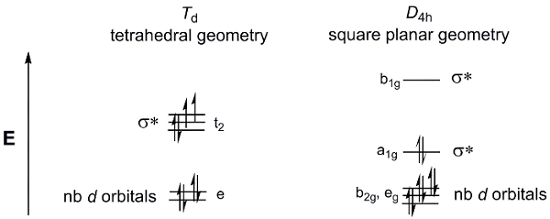
Figura 4. I diagrammi di scissione d-orbitaleper i gruppi di punti Td (tetraedrico) e D4h (quadrato planare).
Ora, considera il conteggio d-elettroniper M (dppf) Cl2. Sia Ni che Pd sono nel Gruppo 10 della tavola periodica. Pertanto, entrambi avranno lo stesso stato di ossidazione (2+) e d-conteggiodegli elettroni (d8). Se riempiamo i due diagrammi di scissione orbitale dsopra con 8 elettroni, vediamo che la geometria planare quadrata risulta in un complesso diamagnetico, mentre il diagramma MO tetraedrico è coerente con una specie paramagnetica. Ci sono diversi fattori che vanno a determinare quale geometria è energeticamente favorita. Nella geometria planare quadrata, ci sono meno elettroni negli orbitali anti-legame, il che indicherebbe che la geometria planare quadrata è più favorita elettronicamente. Tuttavia, dobbiamo anche considerare l'energia necessaria per accoppiare gli elettroni. L'energia di accoppiamento degli elettroni nelle molecole planari quadrate è superiore a quella delle molecole tetraeche, che hanno meno orbitali completamente riempiti. Infine, dobbiamo considerare la quantità di σ*d-orbitali sono destabilizzati. Gli atomi di metallo più grandi hanno una maggiore sovrapposizione spaziale con i ligandi, con conseguente maggiore energia σ* d-orbitali.
Infine, dobbiamo anche considerare il contributo energetico delle repulsioni steriche. La geometria tetraedrica è più favorita stericamente (con angoli di 109,5 °) rispetto alla geometria planare quadrata (90 °). Pertanto, ci sono diversi fattori opposti che influenzano quale geometria è più favorita, data l'identità di M in M(dppf)Cl2.
Saremo in grado di distinguere tra queste due geometrie utilizzando NMR. Se la molecola è planare quadrata, osserveremo una NMR diagnostica 1H di una specie diamagnetica. Se la molecola è tetraedrica, osserveremo segnali paramagnetici nella NMR 1H. Infine, useremo il metodo Evans (vedi il video "Metodo Evans" per maggiori dettagli) per determinare il momento magnetico della soluzione delle specie paramagnetiche.
Procedura
NOTA: Per precauzioni di sicurezza, la sicurezza della linea Schlenk deve essere rivista prima di condurre gli esperimenti. I bicchieri devono essere ispezionati per le crepe delle stelle prima dell'uso. Prestare attenzione per assicurarsi che O2 non sia condensato nella trappola della linea di Schlenk se si utilizza N2liquido . A temperatura N2 liquida, O2 condensa ed è esplosivo in presenza di solventi organici. Se si sospetta che O2 sia stato condensato o che si osservi un liquido blu nella trappola fredda, lasciare la trappola fredda sotto vuoto dinamico. NON rimuovere latrappola N 2 liquida o spegnere la pompa pervuoto. Nel tempo il liquido O2 evaporerà nella pompa; è sicuro rimuovere latrappola N 2 liquida solo dopo che tutto l'O2 è evaporato. Per ulteriori informazioni, vedere il video "Sintesi di un metallocene Ti(III) utilizzando la tecnica della linea di Schlenk". 1
1. Impostazione della linea Schlenk per la sintesi di Ni(dppf)Cl2 e Pd(dppf)Cl2
NOTA: Per una procedura più dettagliata, consultare il video "Schlenk Lines Transfer of Solvent" nella serie Essentials of Organic Chemistry).
- Chiudere la valvola di rilascio della pressione.
- Accendere il gas N2 e la pompa per vuoto.
- Quando il vuoto della linea Schlenk raggiunge la sua pressione minima, preparare la trappola fredda con N2 liquido o ghiaccio secco/acetone.
- Assemblare la trappola fredda.
2. Sintesi di Ni(dppf)Cl2 (Figura 5) in condizioni anaerobiche/inerti
Nota Mentre la sintesi di Ni(dppf)Cl2 può essere condotta in condizioni aerobiche, si ottengono rese più elevate se condotte in condizioni anaerobiche.
- Aggiungere 550 mg di dppf (1 mmol) e 40 ml di isopropanolo a un pallone a tre colli.
Nota dppf può essere acquistato da Sigma Aldrich o sintetizzato utilizzando metodi trovati in letteratura. 2 - Montare il collo centrale del pallone a tre colli con un condensatore e un adattatore per vuoto. Montare i due colli rimanenti con 1 tappo in vetro e 1 setto in gomma.
- Degassare la soluzione facendo gorgogliare il gas N2 attraverso il solvente per 15 min. Utilizzare l'adattatore per vuoto nella parte superiore del condensatore come "sfiato".
- Collegare l'adattatore per vuoto nella parte superiore del condensatore a N2 utilizzando la linea Schlenk.
- Iniziare a riscaldare il matraccio a tre colli a bagnomaria impostato a 90 °C.
- In un matraccio a fondo tondo a collo singolo, aggiungere 237 mg di NiCl2·6H 2O (1 mmol) a 4 mL di una miscela 2:1 di isopropanolo (grado reagente) e metanolo (grado reagente). Sonicare la miscela risultante fino a quando tutto il sale Ni si è sciolto (circa 1 minuto).
NOTA: se un sonicatore non è disponibile, riscaldare delicatamente la miscela a bagnomaria. - Degassare la soluzione Ni facendo gorgogliare il gas N2 attraverso la miscela per 5 min.
- Aggiungere lasoluzionedi NiCl 2 ·6H2O al matraccio rotondo a tre colli tramite trasferimento di cannula.
- Lasciare la reazione al reflusso per 2 ore a 90 °C.
- Lasciare raffreddare la reazione in un bagno di ghiaccio. Isolare il precipitato verde risultante mediante filtrazione sotto vuoto attraverso un imbuto fritto.
- Lavare il prodotto con 10 mL di isopropanolo freddo, seguito da 10 mL di esani.
- Lasciare asciugare il prodotto all'aria prima di preparare il campione NMR.
- Prendere una NMR di 1ora del prodotto in cloroformio-d.
- Se la NMR 1H è indicativa di una specie paramagnetica, preparare una NMR per il metodo Evans, seguendo le istruzioni nel passaggio 4.

Figura 5. Sintesi di Ni(dppf)Cl2.
3. Sintesi di Pd(dppf)Cl2 (Figura 6)1
NOTA: Utilizzare tecniche standard di linea Schlenk per la sintesi di Pd(dppf)Cl2 (vedere il video "Synthesis of a Ti(III) Metallocene Using Schlenk line Technique").
Nota Mentre la sintesi di Pd(dppf)Cl2 può essere condotta in condizioni aerobiche, si ottengono rese più elevate se condotte in condizioni anaerobiche.
- Aggiungere 550 mg (1 mmol) di dppf e 383 mg (1 mmol) di bis(benzonitrile)palladio(II) cloruro in un matraccio Schlenk e preparare il matraccio Schlenk per il trasferimento del solvente con cannula.
- Aggiungere 20 ml di toluene degassato al pallone Schlenk tramite trasferimento di cannula.
- Lasciare che la reazione si agiti per almeno 12 ore a temperatura ambiente.
- Isolare il precipitato arancione risultante mediante filtrazione sotto vuoto attraverso un imbuto fritto.
- Lavare il prodotto con toluene (10 ml), seguito da esani (10 ml).
- Lasciare asciugare il prodotto all'aria prima di preparare il campione NMR.
- Prendere una NMR di 1ora del prodotto in cloroformio-d.
- Se la RMN 1H è indicativa di una specie paramagnetica, preparare una NMR per il metodo Evans seguendo le istruzioni descritte nel passaggio 4.

Figura 6. Sintesi di Pd(dppf)Cl2.
4. Preparazione del campione del metodo Evans
NOTA: per una procedura più dettagliata, fare riferimento al video "Metodo Evans".
- In un flaconcino a scintillazione, preparare una soluzione 50:1 (volume:volume) di cloroformio-d:trifluorotoluene. Pipettare 2 mL di solvente deuterato, e a questo aggiungere 40 μL di trifluorotoluene. Chiudere il flaconcino.
NOTA: In questo esempio, utilizzeremo 19F NMR per osservare lo spostamento del segnale F nel trifluorotoluene in presenza delle specie paramagnetiche. - Con questa soluzione, preparare l'inserto capillare.
- Pesare 10-15 mg del campione paramagnetico in un nuovo flaconcino di scintillazione e annotare la massa.
- Pipetta ~ 600 μL della miscela di solvente preparata nel flaconcino contenente le specie paramagnetiche. Nota la massa. Assicurarsi che il solido si dissolva completamente.
- In un tubo NMR standard, far cadere con attenzione l'inserto capillare ad angolo, per assicurarsi che non si rompa.
- Pipettare la soluzione contenente le specie paramagnetiche nel tubo NMR.
- Acquisisci e salva uno spettro NMR standard da 19F.
- Nota la temperatura della sonda.
- Notare la radiofrequenza.
Risultati
Pd(dppf)Cl2:
1 H NMR (cloroformio-d, 400 MHz, δ, ppm): 4,22 (alfa-H), 4,42 (beta-H), 7,89, 7,44, 7,54 (aromatico)3.
Ni(dppf)Cl2:
1 H NMR (cloroformio-d, 300 MHz, δ, ppm): 20.85, 10.04, 4.23, 3.98, 1.52, -3.31, -7.10.
Metodo Evans, osservando lo spostamento di 19F del trifluorotoluene:
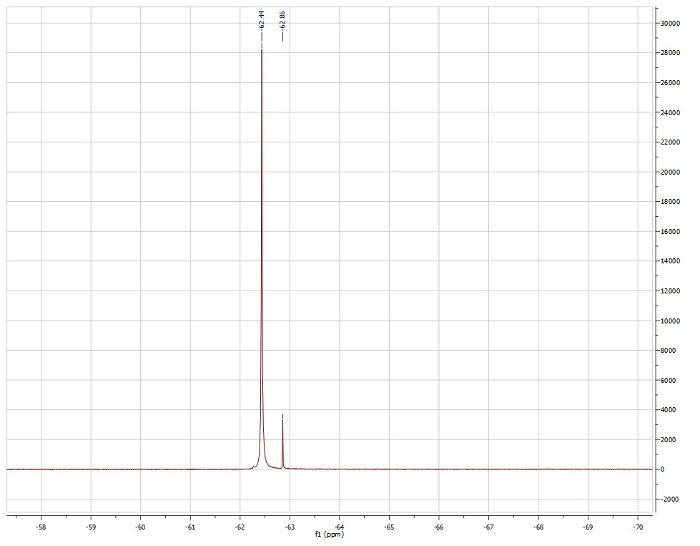
Osservato μeff = 3,15 μb
Massa del campione: 9,5 mg
Massa della soluzione (cloroformio-d + trifluorotoluene): 0,8365 g
Temperatura della sonda: 296.3 K
Campo NMR (MHz): 470,06
Segnalato μeff = 3,39 μb. 4
Per S = 1 (previsto in base alla geometria tetraedrica, Figura 4), μteorico eff = 2,83 μb.
Per S = 3/2, μ teoricaeff = 3,46 μb.
Sulla base dei dati NMR 1H, vediamo che Pd(dppf)Cl2 è diamagnetico e quindi presenta geometria planare quadrata. La NMR 1H di Ni(dppf)Cl2 è paramagnetica e quindi è tetraedrica al centro Ni. Il metodo di Evan conferma che Ni(dppf)Cl2 è paramagnetico, esibendo un momento magnetico di soluzione di 3,15 μb, che è vicino al valore riportato in letteratura per questo composto. Poiché Ni è piccolo, lo sterico supera qualsiasi stabilizzazione elettronica associata alla geometria planare quadrata, rendendo Ni(dppf)Cl2 tetraedrico. D'altra parte, Pd è grande e, quindi, ha una maggiore energia σ* d-orbitali. In questo caso, la stabilizzazione elettronica supera di gran lunga le repulsioni steriche, risultando in una geometria planare quadrata a Pd in Pd(dppf)Cl2.
Applicazione e Riepilogo
Questo video ha dimostrato come la teoria MO possa essere utilizzata come modello di legame in complessi di metalli di transizione. Abbiamo sintetizzato due complessi con la formula generale M(dppf)Cl2. Quando M = Ni, il complesso a 4 coordinate presenta una geometria tetraedrica. Sostituendo l'atomo di Ni con un metallo di transizione più grande (Pd), la molecola assume una geometria planare quadrata.
In precedenza, abbiamo appreso dell'importante ruolo che il ferrocene svolge nel campo della chimica organometallica. I ferroceni sostituiti, incluso il dppf, sono usati come ligandi chelanti per i metalli di transizione1a,2ae3a fila. I complessi risultanti sono utilizzati nella catalisi omogenea (cioè[1,1'-bis(difenilfosfino)ferrocene]palladio(II) dicloruro, Pd(dppf)Cl2, è un catalizzatore per le reazioni di formazione del legame C-C e C-eteroatomo).
Comprendere il legame nei complessi di metalli di transizione è importante per spiegare la loro struttura e reattività. Uno dei punti di forza della teoria MO è che fornisce un buon modello che può essere utilizzato per spiegare la reattività dei complessi di metalli di transizione. In molti casi, il centro metallico è la posizione di qualsiasi reattività esibita dalla molecola. Pertanto, è utile avere un'immagine della densità elettronica al centro del metallo, che è riassunta nel diagramma di scissione orbitale dderivato dalla teoria MO (Figura 3). Si noti che non solo gli MO nel diagramma di scissione orbitale dmostrano per lo più carattere orbitale d(gli orbitali σ* sono più vicini in energia agli orbitali atomici ddel metallo e quindi la maggior parte della densità elettronica in quegli MO è centrata sull'atomo di metallo), ma anche il diagramma di scissione contiene l'HOMO e il LUMO della molecola. Pertanto, qualsiasi chimica che si verifica influenzerà direttamente il diagramma di scissione orbitale ddella molecola.
Riferimenti
- Corain, B., Longato, B., Favero, G. Heteropolymetallic Complexes of 1,1’-Bis(diphenylphosphino)ferrocene (dppf). III*. Comparative Physicochemical Properties of (dppf)MCl2 (M = Co, Ni, Pd, Pt, Zn, Cd, Hg). Inorg Chim Acta. 157, 259-266 (1989).
- Cullen, W. R., Einstein, F. W. B., Jones, T., Kim, T.-J. Structures of three hydrogenation catalysts [(P-P)Rh(NBD)]ClO4 and some comparative rate studies where (P-P) = (η5-R1R2PC5H4)(η5-R3R4PC5H4)Fe (R1 = R2 = R3 = R4 = Ph, R1 = R2 = Ph, R3 = R4 = CMe3, R1 = R3 = Ph, R2 = R4 = CMe3). Organometallics. 4(2), 346-351 (1983).
- Colacot, T. J., C.-Olivares, R., H.-Ortega, S. Synthesis, X-ray, spectroscopic and a preliminary Suzuki coupling screening studies of a complete series of dppfMX2 (M = Pt, Pd, X = Cl, Br, I). J Organomet Chem. 637-639, 691-697 (2001).
- Rudie, A. W., Lichtenberg, D. W., Katcher, M. L., Davison, A. Comparative Study of 1,1’-bis(diphenylphosphino)cobaltocinium hexafluorophosphate and 1,1’-bis(dipenylphosphino)ferrocene as Bidentate Ligands. Inorg Chem. 17(10), 2859-2863, 1978.
Vai a...
Video da questa raccolta:

Now Playing
Teoria degli orbitali molecolari
Inorganic Chemistry
35.3K Visualizzazioni

Sintesi di un Ti(III) metallocene utilizzando la tecnica della linea Schlenk
Inorganic Chemistry
31.6K Visualizzazioni

Scatola a guanti (Glove Box) e sensori di impurezze
Inorganic Chemistry
18.6K Visualizzazioni

Purificazione del ferrocene per sublimazione
Inorganic Chemistry
54.5K Visualizzazioni

Il metodo di Evans
Inorganic Chemistry
68.4K Visualizzazioni

Diffrazione a raggi X su cristallo singolo e su polveri
Inorganic Chemistry
104.3K Visualizzazioni

Spettroscopia di risonanza paramagnetica elettronica (EPR)
Inorganic Chemistry
25.4K Visualizzazioni

Spettroscopia Mössbauer
Inorganic Chemistry
22.0K Visualizzazioni

Interazione acido-base di Lewis in Ph3P-BH3
Inorganic Chemistry
38.8K Visualizzazioni

Struttura del ferrocene
Inorganic Chemistry
79.4K Visualizzazioni

Applicazione della teoria dei gruppi nella spettroscopia infrarossa
Inorganic Chemistry
45.1K Visualizzazioni

Paddlewheel a quadruplo legame metallo-metallo
Inorganic Chemistry
15.3K Visualizzazioni

Celle di Grätzel (Dye-sensitized Solar Cells)
Inorganic Chemistry
15.8K Visualizzazioni

Sintesi di un complesso di cobalto (II) legato ad ossigeno
Inorganic Chemistry
51.6K Visualizzazioni

Inizio fotochimico di una reazione di polimerizzazione radicalica
Inorganic Chemistry
16.7K Visualizzazioni