Teoría del orbital molecular (MO)
Visión general
Fuente: Tamara M. Powers, Departamento de química, Texas A & M University
Este protocolo sirve como guía en la síntesis de dos complejos del metal con el ligando 1, 1'-bis (difenilfosfino) ferroceno (dppf): M (dppf) Cl2, donde M = Ni o Pd. Mientras que ambos de estos complejos de metales de transición son 4 coordenadas, exhiben distintas geometrías en el centro de metal. Con teoría orbital molecular de (MO) en conjunto con 1H NMR y el método de Evans, determinamos la geometría de estos dos compuestos.
Principios
Hay una gran variedad de modelos que los químicos usan para describir el enlace en las moléculas. Es importante recordar que los modelos son representaciones de sistemas y por lo tanto tienen ventajas pero también limitaciones importantes. Por ejemplo, estructuras de puntos de Lewis, el método más simple para describir cómo los átomos comparten electrones, no toman en cuenta la geometría de los átomos en la molécula. Teoría de repulsión de par de electrones de Shell de la Valencia (VSEPR) describir la geometría de los átomos, pero no proporciona una explicación para la observación de que especie de enlace con el mismo número de electrones de Valencia puede exhibir geometrías diferentes. Especialmente para los complejos de metales de transición, tanto de estos modelos se quedan cortas al describir la Unión de metales. Teoría del campo cristalino es un modelo de vinculación que es específico de complejos de metales de transición. Este modelo analiza los efectos de campo de eléctrico de un ligando a los orbitales atómicos d o f de un centro de metal. La interacción resulta en una rotura en la degeneración de los orbitales atómicos.
En este video, nos centraremos en la teoría de la MO, que es un modelo potente que puede utilizarse para describir la vinculación no sólo moléculas del grupo principal, pero también es conveniente para el modelado de la vinculación en complejos de metales de transición. Aquí, demostramos cómo generar un esquema de MO de metal-que contienen compuestos.
Teoría de la MO:
MO la teoría describe la vinculación química como la combinación lineal de orbitales atómicos (LCAO) de cada átomo en un compuesto dado. El MOs de LCAOs que describen la geometría y la energía de los electrones compartidos por un número de átomos en la molécula (es decir, la direccionalidad y la fuerza de los enlaces formados por átomos teniendo en cuenta).
Para revisar los fundamentos de la teoría de la MO, primero consideremos la molécula diatómica F2 (diagrama completo de MO en la figura 1). Un átomo de flúor tiene 4 orbitales atómicos de Valencia: 2s, 2px, 2pyyp2z. El orbital 2s es más bajo en energía que los orbitales atómicos 2p , que todos tienen la misma energía. Una combinación lineal de orbitales atómicos se produce entre orbitales atómicos de energía similar y de coincidencia de simetría. En este caso, el orbitals 2 en un átomo de F va a interactuar con las 2s orbital de otro átomo de F. La adición de estos dos orbitales da como resultado la formación de un σ vinculación MO (figura 1). La vinculación es una interacción estabilizante y, por lo tanto, la resultante σ MO es más baja en energía en relación con la energía de los orbitales atómicos des 2. Restar los 2 resultados de orbitarios des en una interacción de anti-bonding (desestabilizadoras), designado como σ *, que es más alta en energía en comparación con los 2 orbitales atómicoss (figura 1).

Figura 1. Diagrama de MO de F2.
Además, los 2 orbitales atómicosp combinará la vinculación y las interacciones de la vinculación. Como los 2 orbitales atómicoss , los 2 orbitales atómicosz p(que a lo largo de la bond F-F) forman interacciones σ y σ *. Si consideramos el 2px ypy orbitales atómicos, vemos que forman diferentes tipos de vinculación y anti-bonding interacciones, llamadas π y π *, respectivamente (figura 1). Es fácil distinguir entre σ y π bonos porque orbitarios de la vinculación del σ son cilíndrico simétricos respecto del eje internuclear, mientras que los orbitales π tienen un plano nodal a lo largo del eje internuclear. El solapamiento espacial de orbitales atómicos que se forman enlaces σ es mayor que el traslapo espacial entre orbitales atómicos que forman enlaces π. Por lo tanto, la resultante π y π * MOs son menos estabilizados y desestabilizadas, respectivamente, en comparación con el MOs σ y σ *, formado por los 2 orbitales atómicos dez p. Entonces podemos llenar el MOs con los electrones de Valencia para los dos átomos de F.
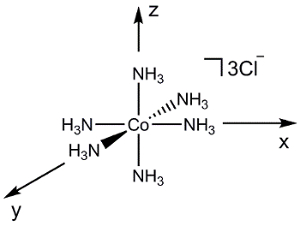
Ahora consideremos una molécula más compleja como [Co (NH3)6] Cl3 (figura 2). Si tuviéramos que utilizar el mismo proceso que anteriormente (teniendo en cuenta la superposición de orbital Atómica entre 2 átomos a la vez), generando un esquema de MO de esta molécula sería extremadamente difícil. En cambio, podemos utilizar teoría del grupo para primero generar una combinación lineal de simetría adaptada (SALC) de los ligandos. Entonces podemos usar la simetría para determinar las interacciones de vinculación/anti-bonding que se forman entre los orbitales atómicos en el metal y las resultantes SALCs.
| O h | E | 8C3 | 6C2 | 6C4 | 3C2' | me | 6S4 | 8S6 | 3σh | 3σd | ||
| A1 g | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | x2+ y2+ z2 | |
| Un2 g | 1 | 1 | -1 | -1 | 1 | 1 | -1 | 1 | 1 | -1 | ||
| Eg | 2 | -1 | 0 | 0 | 2 | 2 | 0 | -1 | 2 | 0 | (2z2- x2-y2, x2-y2) | |
| T1 g | 3 | 0 | -1 | 1 | -1 | 3 | 1 | 0 | -1 | -1 | (Rx, RyRz) | |
| T2 g | 3 | 0 | 1 | -1 | -1 | 3 | -1 | 0 | -1 | 1 | (xz, yz, xy) | |
| Un1u | 1 | 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | ||
| Un2u | 1 | 1 | -1 | -1 | 1 | -1 | 1 | -1 | -1 | 1 | ||
| Eu | 2 | -1 | 0 | 0 | 2 | -2 | 0 | 1 | -2 | 0 | ||
| T1u | 3 | 0 | -1 | 1 | -1 | -3 | -1 | 0 | 1 | 1 | (x, y, z) | |
| T2u | 3 | 0 | 1 | -1 | -1 | -3 | 1 | 0 | 1 | -1 | ||
| Γ rojo | 6 | 0 | 0 | 2 | 2 | 0 | 0 | 0 | 4 | 4 |
Γ rojo = A 1 g + E g + T 1U
Figura 2. Combinación lineal de orbitales atómicos ligando de Cl [Co (NH3)6]3.
Para generar el SALCs [Co (NH3)6]3 +, seguimos un procedimiento similar descrito en la "teoría del grupo" video de la serie de Química inorgánica :
1. determinar el grupo de punto de la molécula.
2. generar una representación reducible de los orbitarios atómicos de ligando.
3. reducir la representación reducible a las representaciones irreducibles.
[Co (NH3)6] 3 + es en el punto de grupo Oh. Puesto que sólo estamos preocupados por la vinculación en el centro de metal, podemos simplemente considerar los 2 orbitales atómicoss en cada ligando de NH3 . Si seguimos los pasos 1-3 para el N 2s, orbitales encontramos que la representación reducible es Γrojo = un1 g + Eg + T1u (figura 2). Mientras que el conjuntog 1 representa 1 SALC, la E,g y T1u conjuntos representan realmente SALCs 2 y 3, respectivamente, dando un total de 6 SALCs (el mismo número de ligandos en el catión [Co (NH3)6]3 +). El 2 SALCs en el set deg E tienen la misma simetría y se traducirá en MOs degenerados cuando interaccionan con los orbitales atómicos del Co (lo mismo puede decirse de las 3 SALCs en el set de1u de T). Utilizando la tabla de caracteres en la figura 2, podemos determinar cómo transforman los orbitarios atómicos de Co en el grupo de punto deh O. Por ejemplo, el dz2 y dx2– y2 orbitales forman un conjunto deg E. Ya que tenemos 2 SALCs ligando con simetría deg E, ésos SALCs forman interacciones de vinculación/anti-bonding y el dz2 dx2 –y2 orbitales atómicos de Co. Continuando de la misma manera para todos los orbitales atómicos de Valencia de Co, se genera un diagrama de MO para el metal de transición complejo, se muestra en la figura 3. Tenga en cuenta que el resto d-orbitarios (dxzyzde d y dxy) transformar como un conjunto (T2 g) pero no tienen una adecuada simetría emparejado SALC. Por lo tanto estos orbitales atómicos se convierten en "no vinculación" MOs. En otras palabras, no participan en la vinculación con los ligandos de este metal de transición complejo.
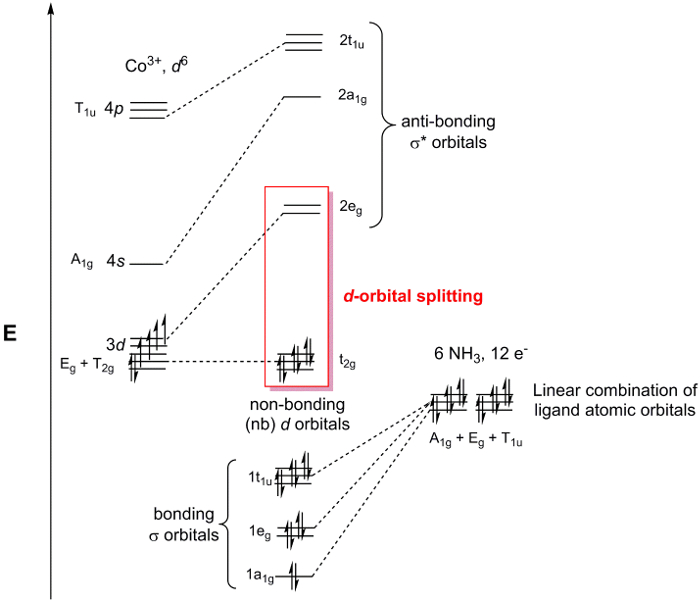
Figura 3. Diagrama de MO para Cl [Co (NH3)6]3.
En la figura 3 se destacan la no vinculación de d-orbitarios y los orbitales σ * d-carácter orbital. Cuando este grupo de MOs se considera por separado en el diagrama de MO todo se refiere a como la d-orbital partir diagrama de un metal de transición complejo. Desde el d-orbital partir diagrama contiene el HOMO y el LUMO, que suelen ser los orbitarios más importantes para entender la química y espectroscopia de complejos de coordinación, químicos a menudo se referirán a la d-orbital dividir el diagrama en lugar del todo diagrama de MO. Convenientemente, el d-orbital diagrama de separación puede ser llenado con el número de– en el centro de metal, ya que los electrones del ligand-basado siempre llenan el MOs σ basado en el diagrama de MO.
Teniendo en cuenta la d -diagramas de separación orbital para M() dppf) Cl2:
Considere un simple 4-coordenadas metal complejo MX4. MX4 puede existir en dos geometrías: tetraédrica o cuadrada plana. D-orbital partir esquemas para lo grupos Td (tetraédrica) y D4 h (cuadrado planar) se muestra en la figura 4. Mientras que los complejos metal general M (dppf) Cl2 no tienen 4 ligandos equivalentes y por lo tanto no están en el punto grupos Td o el D4 h, todavía podemos utilizar estos d-orbital partir diagramas como un modelo para describir el d -MOs orbitales para las dos geometrías posibles.
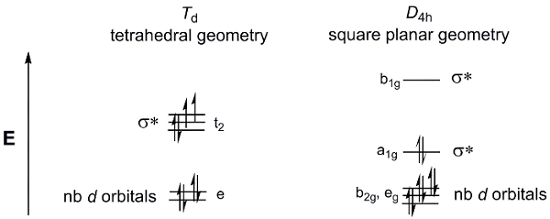
Figura 4. D-orbital diagramas para el punto de división grupos Td (tetraédrica) y D4 h (cuadrado planar).
Ahora, consideremos el d-cuenta electrónica para M (dppf) Cl2. Pd y Ni están en el grupo 10 de la tabla periódica. Por lo tanto, ambos tienen el mismo estado de oxidación (2 +) y d-conteo de electrones (d8). Si llenamos los dos d-diagramas de separación orbitales sobre con 8 electrones, vemos que la geometría cuadrado planar da en un complejo diamagnético, mientras que el diagrama de MO tetraédrico es consistente con una especie paramagnética. Hay varios factores que van a determinar que geometría es favorecida energéticamente. En la geometría cuadrado planar, hay pocos electrones en orbitarios anti-bonding, lo que indicaría que la geometría cuadrado planar es más electrónicamente favorecido. Sin embargo, también debemos considerar la energía requerida para los electrones del par. El electrón vinculación energía en las moléculas planares cuadrado es mayor que en moléculas tetraédricas, que tienen menos orbitarios completamente llenas. Por último, debemos tener en cuenta la cantidad σ * d-orbitarios se desestabilizaron. Átomos metálicos más grandes tienen una mayor superposición espacial con ligandos, lo que resulta en mayor energía σ * d-orbitarios.
Finalmente, también tenemos que considerar la contribución de la energía de repulsión estérica. Geometría tetraédrica es más sterically favorecidas (con ángulos de 109,5 °) en comparación con geometría cuadrado planar (90 °). Por lo tanto, hay varios factores opuestos que afectan que geometría es más favorecida, dada la identidad de M en M (dppf) Cl2.
Seremos capaces de distinguir entre estas dos geometrías mediante RMN. Si la molécula es planar cuadrado, observamos un diagnóstico 1H NMR de unespecies diamagnéticos. Si la molécula es tetraédrica, observamos señales paramagnéticas en el 1H NMR. Por último, utilizamos el método de Evans (ver el video de "Método de Evans" para más detalles) para determinar el momento magnético de solución de la especie paramagnética.
Procedimiento
Nota: Como medida de seguridad, la seguridad de la línea de Schlenk debe revisarse antes de realizar los experimentos. Vidrio debe ser inspeccionado para estrellas grietas antes de usar. Debe tenerse cuidado para asegurar que el O2 no se condensa en la trampa de la línea de Schlenk si utiliza líquido N2. Temperaturas líquido N2 , O2 se condensa y es explosivo en presencia de solventes orgánicos. Si se sospecha que ha sido condensado O2 o un líquido de color azul se observa en la trampa de frío, deje que la trampa fría bajo vacío dinámico. No retire el líquido N2 purgador o apagar la bomba de vacío. Con el tiempo se evaporará el líquido O2 a la bomba; sólo es seguro remover la trampa de2 N líquida una vez que se haya evaporado todo el O2 . Para obtener más información, ver el video de "Síntesis de una línea de Schlenk de uso de metaloceno Ti(III) técnica". 1
1. configuración de la línea de Schlenk para la síntesis de Ni (dppf) Cl2 y Pd (dppf) Cl2
Nota: Para un procedimiento más detallado, por favor revisar el video "Schlenk líneas transferencia de disolvente" de la serie de fundamentos de química orgánica ).
- Cierre la válvula de liberación de presión.
- Encienda el gas de N2 y la bomba de vacío.
- Como el Schlenk línea vacío alcanza su presión mínima, preparar la trampa de frío con hielo seco/acetona o líquido N2 .
- Montar la trampa de frío.
2. síntesis de Ni (dppf) Cl2 (figura 5) en condiciones anaerobias/inerte
Nota mientras que la síntesis de Ni (dppf) Cl2 puede llevarse a cabo en condiciones aeróbicas, mayores rendimientos se obtienen cuando se llevó a cabo en condiciones anaeróbicas.
- Añadir dppf 550 mg (1 mmol) y 40 mL de isopropanol a un matraz de cuello de tres.
Dppf nota puede adquirirse en Sigma Aldrich o sintetizados utilizando métodos encontrados en la literatura. 2 - Ajuste el cuello de centro del matraz de cuello de tres con un condensador y un adaptador de vacío. Montar los dos cuellos restantes con tapón de vidrio de 1 y 1 membrana de goma.
- Desgasificar la solución por los burbujeantes N2 gas a través del solvente para uso a 15 minutos del adaptador de vacío en la parte superior del condensador como el "vent".
- Conecte el adaptador de vacío en la parte superior del condensador de N2 usando la línea de Schlenk.
- Empezar a calentar el matraz de cuello de tres en un baño de agua a 90 ° C.
- En un solo cuello redondo matraz de fondo, añadir 237 mg NiCl2·6H2O(1 mmol) a 4 mL de una mezcla 2:1 de isopropanol (grado reactivo) y metanol (grado reactivo). Someter a ultrasonidos la mezcla resultante hasta que toda la sal de Ni se disuelva (aproximadamente 1 min).
Nota: Si no encuentra un sonicador, caliente suavemente la mezcla en un baño de agua. - Desgasificar la solución Ni por los burbujeantes N2 gas a través de la mezcla durante 5 minutos.
- Añadir la NiCl2·6H2O solución al matraz de fondo redondo cuello de tres vía transferencia de cánula.
- Permite la reacción a reflujo durante 2 h a 90 ° C.
- Permita que la reacción se enfríe en un baño de hielo. Aislar el precipitado verde resultante por filtración de vacío a través de un embudo de sinterizado.
- Lave el producto con 10 mL de isopropanol frío, seguido de 10 mL de hexanes.
- Seque el producto al aire, antes de preparar la muestra de NMR.
- Tome un 1H NMR del producto en cloroformo -d.
- Si el 1H NMR es indicativo de una especie paramagnética, preparar un NMR para el método de Evans, siguiendo las instrucciones en el paso 4.

Figura 5. Síntesis de Ni (dppf) Cl2.
3. síntesis de la EP (dppf) Cl2 (figura 6)1
Nota: Utilizar técnicas de línea de Schlenk estándar para la síntesis de la EP (dppf) Cl2 (ver el video de "Síntesis de una línea de Schlenk de uso de metaloceno Ti(III) técnica").
Nota mientras que la síntesis de la EP (dppf) Cl2 puede llevarse a cabo en condiciones aeróbicas, mayores rendimientos se obtienen cuando se llevó a cabo en condiciones anaeróbicas.
- Añadir dppf 550 mg (1 mmol) y 383 mg (1 mmol) de cloruro de bis(benzonitrile)palladium(II) a un matraz Schlenk y preparar el matraz Schlenk para la transferencia de la cánula de solvente.
- Añadir 20 mL de tolueno desgasificada al matraz Schlenk vía transferencia de la cánula.
- Permite la reacción a agitar durante al menos 12 h a temperatura ambiente.
- Aislar el precipitado resultante de la naranja por la filtración de vacío a través de un embudo de sinterizado.
- Lave el producto con tolueno (10 mL), seguido por hexanes (10 mL).
- Seque el producto al aire, antes de preparar la muestra de NMR.
- Tome un 1H NMR del producto en cloroformo -d.
- Si el 1H NMR es indicativo de una especie paramagnética, preparar un NMR para el método de Evans siguiendo las instrucciones descritas en el paso 4.

Figura 6. Síntesis de la EP (dppf) Cl2.
4. preparación de la muestra del método de Evans
Nota: Para un procedimiento más detallado, consulte el vídeo de "Método de Evans".
- En un vial de centelleo, preparar una solución de 50: 1 (volumen: el volumen) de cloroformo -d: trifluorotoluene. Pipeta 2 mL de disolventes deuterados y a esto agregar 40 μl de trifluorotoluene. Tapa el frasco.
Nota: En este ejemplo, utilizaremos 19F RMN para observar el cambio de la señal F en trifluorotoluene en presencia de la especie paramagnética. - Con esta solución, preparar el relleno capilar.
- Pesa 10-15 mg de la muestra paramagnética en un vial de centelleo nuevo y anote la masa.
- Pipeta de ~ 600 μl de la mezcla solvente preparada en el frasco que contiene la especie paramagnética. Tenga en cuenta la masa. Asegúrese de que el sólido disuelve totalmente.
- En un tubo estándar de NMR, caer cuidadosamente el inserto capilar en ángulo, para no romper.
- Pipetear la solución que contiene las especies paramagnéticas en el tubo NMR.
- Adquirir y guardar un estándar 19F NMR espectro.
- Tenga en cuenta la temperatura de la sonda.
- Tenga en cuenta la radiofrecuencia.
Resultados
Pd (dppf) Cl2:
1 H RMN (cloroformo -d, 400 MHz, δ, ppm): 4.22 (alfa-H), 4.42 (beta-H), 7.89, 7,44, 7,54 (aromático)3.
Ni (dppf) Cl2:
1 H RMN (cloroformo -d, 300 MHz, δ, ppm): 20.85 10.04, 4.23, 3.98, 1.52,-3.31,-7.10.
Método de Evans, mirando el cambio 19F de trifluorotoluene:
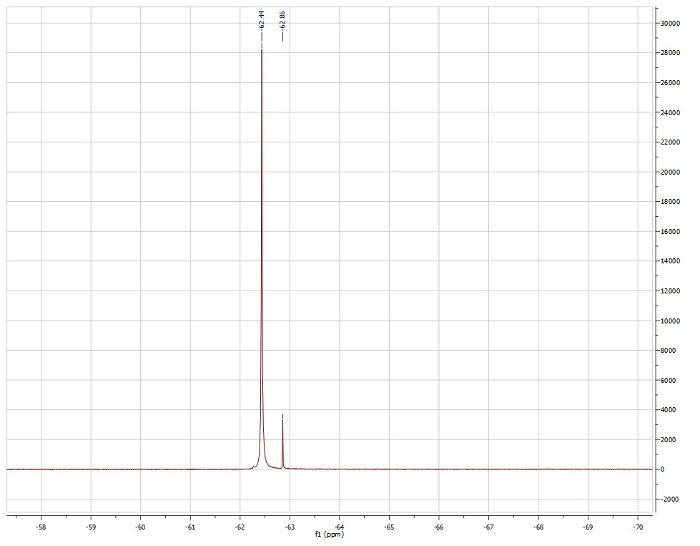
Observadoμeff = 3.15 μb
Masa de la muestra: 9,5 mg
Masa de solución (cloroformo -d + trifluorotoluene): 0,8365 g
Temperatura de la sonda: 296,3 K
Campo de RMN (MHz): 470.06
Informó μeff = 3.39 μb. 4
Para S = 1 (predicho basado en geometría tetraédrica, figura 4), teórica μeff = 2.83 μb.
Para S = 3/2, teórica μeff = 3.46 μb.
Basado en 1datos NMR de H, vemos que el Pd (dppf) Cl2 es diamagnético y por lo tanto exhibe una geometría cuadrado planar. 1H NMR de Ni (dppf) Cl2 es paramagnético y por lo tanto es tetraédrico en el centro de Ni. Método de Evan confirma que Ni (dppf) Cl2 es paramagnético, exhibiendo un momento magnético de solución de 3.15 μb, que está cerca de la literatura informó valor para este compuesto. Puesto que Ni es pequeña, el sterics compensa cualquier estabilización electrónica asociada con la geometría cuadrado planar, que Ni (dppf) Cl2 tetraédrico. Por otro lado, Pd es grande y, por lo tanto, tiene mayor energía σ * d-orbitarios. En este caso, la estabilización electrónica compensa grandemente la repulsión estérica, dando como resultado una geometría cuadrado planar en el Pd de la Pd (dppf) Cl2.
Aplicación y resumen
Este video demuestra cómo la teoría MO puede ser utilizado como un modelo de vinculación en los complejos de metales de transición. Sintetizan dos complejos con el fórmula general M (dppf) Cl2. Cuando M = Ni, las exposiciones complejas 4 coordenada una geometría tetraédrica. Reemplazar el átomo Ni con un metal de transición más grande (Pd), la molécula tiene geometría cuadrado planar.
Anteriormente, hemos aprendido sobre el importante papel que desempeña el ferroceno en el campo de la química organometálica. Ferrocenes substituidos, incluyendo dppf, se utiliza como quelante ligandos para 1st, 2ndy 3rd fila metales de transición. Los complejos resultantes se utilizan en la catálisis homogénea (es decir., [dicloruro 1,1'-bis(diphenylphosphino)ferrocene]palladium(II), Pd (dppf) Cl2, es un catalizador para reacciones de formación de enlace C-C y C-heteroatom).
Entender la vinculación en complejos de metales de transición es importante para explicar su estructura y reactividad. Uno de los puntos fuertes de la teoría MO es que proporciona un buen modelo que puede utilizarse para explicar la reactividad de complejos de metales de transición. En muchos casos, el centro de metal es la ubicación de cualquier reactividad de la molécula. Por lo tanto, es valioso tener una imagen de la densidad del electrón en el centro de metal, que se resume en el d -orbital división diagrama derivado de la teoría de MO (figura 3). Aviso que no solamente el MOs En el d-orbital diagrama que exhiben sobre todo d-carácter orbital (los orbitales σ * son los más cercanos en energía para el atómico d-orbitarios del metal y por lo tanto la mayor parte de la densidad del electrón en los MOs es centrado en el átomo del metal), pero también el diagrama que contiene el HOMO y el LUMO de la molécula. Por lo tanto, cualquier química que se produce afectará directamente el d-orbital dividir el diagrama de la molécula.
Referencias
- Corain, B., Longato, B., Favero, G. Heteropolymetallic Complexes of 1,1’-Bis(diphenylphosphino)ferrocene (dppf). III*. Comparative Physicochemical Properties of (dppf)MCl2 (M = Co, Ni, Pd, Pt, Zn, Cd, Hg). Inorg Chim Acta. 157, 259-266 (1989).
- Cullen, W. R., Einstein, F. W. B., Jones, T., Kim, T.-J. Structures of three hydrogenation catalysts [(P-P)Rh(NBD)]ClO4 and some comparative rate studies where (P-P) = (η5-R1R2PC5H4)(η5-R3R4PC5H4)Fe (R1 = R2 = R3 = R4 = Ph, R1 = R2 = Ph, R3 = R4 = CMe3, R1 = R3 = Ph, R2 = R4 = CMe3). Organometallics. 4(2), 346-351 (1983).
- Colacot, T. J., C.-Olivares, R., H.-Ortega, S. Synthesis, X-ray, spectroscopic and a preliminary Suzuki coupling screening studies of a complete series of dppfMX2 (M = Pt, Pd, X = Cl, Br, I). J Organomet Chem. 637-639, 691-697 (2001).
- Rudie, A. W., Lichtenberg, D. W., Katcher, M. L., Davison, A. Comparative Study of 1,1’-bis(diphenylphosphino)cobaltocinium hexafluorophosphate and 1,1’-bis(dipenylphosphino)ferrocene as Bidentate Ligands. Inorg Chem. 17(10), 2859-2863, 1978.
Tags
Saltar a...
Vídeos de esta colección:

Now Playing
Teoría del orbital molecular (MO)
Inorganic Chemistry
35.1K Vistas

Síntesis de un metaloceno Ti(III) utilizando la técnica de línea de Schlenk
Inorganic Chemistry
31.5K Vistas

Guantera y sensores de impureza
Inorganic Chemistry
18.6K Vistas

Purificación de ferroceno por sublimación
Inorganic Chemistry
54.3K Vistas

El método de Evans
Inorganic Chemistry
67.9K Vistas

Difracción de rayos X de monocristal y de polvos
Inorganic Chemistry
103.9K Vistas

Espectroscopía de resonancia paramagnética electrónica (EPR)
Inorganic Chemistry
25.3K Vistas

Espectroscopía de Mössbauer
Inorganic Chemistry
21.9K Vistas

Interacción ácido-base de Lewis en Ph3P-BH3
Inorganic Chemistry
38.7K Vistas

Estructura del ferroceno
Inorganic Chemistry
79.1K Vistas

Aplicación de la teoría de grupos a la espectroscopía infrarroja
Inorganic Chemistry
44.9K Vistas

Enlance cuadruple de metal a metal en complejos de tipo rueda de paletas
Inorganic Chemistry
15.3K Vistas

Celdas solares teñidas con colorante
Inorganic Chemistry
15.7K Vistas

Síntesis de un complejo de cobalto (II) que transporta oxígeno
Inorganic Chemistry
51.5K Vistas

Iniciación fotoquímica de reacciones de polimerización por radicales libres
Inorganic Chemistry
16.7K Vistas
ACERCA DE JoVE
Copyright © 2025 MyJoVE Corporation. Todos los derechos reservados