Molekülorbital (MO)-Theorie
Überblick
Quelle: Tamara M. Powers, Department of Chemistry der Texas A & M University
Dieses Protokoll dient als Leitfaden bei der Synthese von zwei Metallkomplexe mit dem Liganden 1, 1'-Bis (Diphenylphosphino) Ferrocen (Dppf): M (Dppf) Cl2, wo M = Ni oder Pd. Während beide dieser Übergang Metall komplexe 4-Koordinate sind, weisen sie unterschiedliche Geometrien an das Metallzentrum. Mit molekularen orbital (MO)-Theorie in Verbindung mit 1H NMR und Evans Methode, bestimmen wir die Geometrie dieser beiden Verbindungen.
Grundsätze
Es gibt eine Vielzahl von Modellen, die Chemiker verwenden, um die Bindung in Molekülen zu beschreiben. Es ist wichtig zu bedenken, dass Modelle Darstellungen von Systemen sind und stärken, aber auch wichtige Einschränkungen. Zum Beispiel Lewis Dot Strukturen, die einfachste Methode zur Beschreibung, wie die Atome Elektronen, teilen nicht die Geometrie der Atome im Molekül berücksichtigen. Valence Shell Electron Pair Repulsion (VSEPR) Theorie beschreibt die Geometrie der Atome, sondern es liefert keine Erklärung für die Beobachtung, dass isoelectronic Arten mit der gleichen Anzahl von Valenzelektronen unterschiedliche Geometrien aufweisen können. Vor allem für Übergang Metall komplexe fallen die beiden Modelle kurz beschreiben das Verkleben von Metallen. Kristall-Feldtheorie ist eine Verklebung Modell, das spezifisch für Übergang Metall komplexe. Dieses Modell sieht die Wirkungen des elektrischen Feldes eines Liganden auf d oder f atomaren orbitale von einem Metallzentrum. Die Interaktion führt zu einer Pause Entartung dieser atomaren orbitale.
In diesem Video konzentrieren wir uns auf MO-Theorie, die ein leistungsfähiges Modell, das kann zur Verklebung in nicht nur Hauptgruppe Moleküle zu beschreiben, sondern ist auch geeignet für die Verklebung in Übergang Metall komplexe Modellierung. Wir zeigen hier, wie eine MO-Diagramm des metallhaltigen generiert Verbindungen.
MO-Theorie:
MO-Theorie beschreibt chemische Bindung als Linearkombination der atomaren orbitale (LCAO) jedes Atom in einer gegebenen Verbindung. MOs, die aus LCAOs resultieren beschreiben die Geometrie und die Energie der Elektronen geteilt durch Anzahl der Atome im Molekül (d.h., Ausrichtung und Stärke der Anleihen von bestimmten Atomen gebildet).
Um die Grundlagen der MO-Theorie zu überprüfen, betrachten wir zuerst die zweiatomiges Molekül F2 (volle MO-Diagramm in Abbildung 1). Eine Fluor-Atom hat 4 Valenz atomaren orbitale: 2s, 2pXundp-2y2p-Z. Die 2s -Orbital ist weniger Energie als die 2p atomaren orbitale, die alle die gleiche Energie haben. Eine Linearkombination der atomaren orbitale treten zwischen atomaren orbitale ähnliche Energie und der passenden Symmetrie. In diesem Fall wird dem 2s -Orbital auf ein F-Atom mit dem 2s orbital auf die anderen F-Atom interagieren. Der Zusatz von diesen zwei orbitale führt zur Bildung einer σ Bindung MO (Abbildung 1). Kleben ist eine stabilisierende Wechselwirkung und die daraus resultierende σ MO deshalb niedriger Energie bezogen auf die Energie der 2s atomaren orbitale. Subtrahieren von 2s -orbitale Ergebnisse in einer Anti-Bonding-Interaktion (destabilisieren), bezeichnet als σ *, ist die höhere Energie im Vergleich zu den 2s atomaren orbitale (Abbildung 1).

Abbildung 1. MO-Diagramm von F2.
Ebenso werden die 2p atomaren orbitale Form kleben und Anti-Verklebung Interaktionen kombinieren. Die 2pz atomaren orbitale (die Lagen entlang der F-F-Bindung) bilden wie die 2s atomaren orbitale σ und σ * Interaktionen. Wenn wir die 2pX undp2y atomaren orbitale betrachten, sehen wir, dass sie verschiedene Arten von Bindung und Anti-Bindung bilden Interaktionen, π und π *, genannt (Abbildung 1). Es ist einfach zu σ π Bindungen unterscheiden weil σ-Bindung-orbitale zylindrisch über die internuklearen Achse symmetrisch sind, während π-orbitale ein Knotenpunkt Flugzeug entlang der internuklearen Achse haben. Die räumliche Überschneidungen zwischen atomaren orbitale, die σ-Bindungen bilden ist größer als die räumliche Überschneidungen zwischen atomaren orbitale, die π-Bindungen bilden. Daher sind die resultierende π und π * MOs weniger stabilisiert und destabilisiert, bzw., im Vergleich zu gebildet durch die 2pz atomaren orbitale σ und σ * MOs. Wir können dann die MOs mit der Valenzelektronen für die zwei F-Atome füllen.
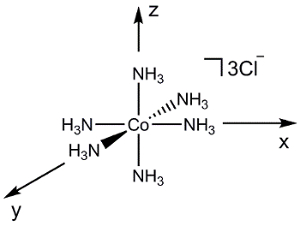
Betrachten wir nun eine komplexere Molekül wie [Co (NH3)6] Cl3 (Abbildung 2). Würden wir den gleichen Prozess wie oben (unter Berücksichtigung der atomaren orbitalen Überschneidungen zwischen 2 Atome zu einem Zeitpunkt) verwenden, wäre erzeugen eine MO-Diagramm dieses Moleküls extrem schwierig. Gruppentheorie können wir stattdessen zuerst eine Linearkombination der Symmetrie angepasst (SALC) der Liganden erzeugen. Symmetrie können wir dann um die Verklebung/anti-bonding Interaktionen zu bestimmen, die zwischen den atomaren orbitale auf dem Metall und der daraus resultierenden SALCs bilden.
| O h | E | 8C3 | 6C2 | 6C4 | 3C-2" | Ich | 6S4 | 8S6 | 3σh | 3σd | ||
| Ein1 g | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | x2+ y2+ Z2 | |
| Ein2 g | 1 | 1 | -1 | -1 | 1 | 1 | -1 | 1 | 1 | -1 | ||
| Eg | 2 | -1 | 0 | 0 | 2 | 2 | 0 | -1 | 2 | 0 | (2z2- X2-y2x2-y2) | |
| T1 g | 3 | 0 | -1 | 1 | -1 | 3 | 1 | 0 | -1 | -1 | (RX, R-y, R-Z) | |
| T2 g | 3 | 0 | 1 | -1 | -1 | 3 | -1 | 0 | -1 | 1 | (Xz, Yz, Xy) | |
| Ein1u | 1 | 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | ||
| Ein2u | 1 | 1 | -1 | -1 | 1 | -1 | 1 | -1 | -1 | 1 | ||
| Eu | 2 | -1 | 0 | 0 | 2 | -2 | 0 | 1 | -2 | 0 | ||
| T-1u | 3 | 0 | -1 | 1 | -1 | -3 | -1 | 0 | 1 | 1 | (X, y, Z) | |
| T-2u | 3 | 0 | 1 | -1 | -1 | -3 | 1 | 0 | 1 | -1 | ||
| Γ rot | 6 | 0 | 0 | 2 | 2 | 0 | 0 | 0 | 4 | 4 |
Γ rot = A 1 g + E g + T 1U
Abbildung 2. Lineare Kombination von Liganden atomaren orbitale [Co (NH3)6] Cl3.
Um die SALCs für [Co (NH3)6]3 +zu generieren, verfolgen wir eine ähnliche Vorgehensweise skizziert in der "Gruppentheorie" video in der Anorganischen Chemie -Serie:
1. bestimmen der Punktgruppe des Moleküls.
(2) erzeugen Sie eine reduzierbar Darstellung der Liganden atomaren orbitale.
3. reduzieren Sie die reduzierbar Vertretung bei irreduziblen Darstellungen.
[Co (NH3)6] 3 + ist in dem Punkt Gruppe Oh. Da wir nur über die Bindung an das Metallzentrum besorgt sind, können wir betrachten Sie einfach die 2s atomaren orbitale auf jedem NH3 Liganden. Wenn wir die Schritte 1-3 für die N 2sorbitale finden wir, dass die reduzierbar Darstellung Γrot = ein1 g + Eg + T1u (Abbildung 2). Während ein1 g Satz 1 SALC darstellt, repräsentieren die Eg und T-1u -Sets tatsächlich 2 und 3 SALCs, was eine Gesamtzahl von 6 SALCs (die gleiche Anzahl von Liganden in das kation [Co (NH3)6]3 +). 2 SALCs in der E-g -Gruppe haben die gleiche Symmetrie und werden in entarteten MOs führen, wenn sie mit der atomaren orbitale des Co interagieren (das gleiche kann über die 3 SALCs im T-1u -Satz gesagt). Mithilfe der Zeichentabelle in Abbildung 2, können wir feststellen, wie die atomaren orbitale Co in der O-h -Punktgruppe verwandeln. Zum Beispiel bilden die dZ2 und dX2, y2 orbitale Fahrgast-/Eg . Da wir 2 Liganden SALCs mit E-g -Symmetrie haben, werden diese SALCs Verklebung/anti-bonding Interaktionen mit der dZ2 und dX2,y2 Co atomaren orbitale bilden. Weiterbildung in der gleichen Weise für alle der Valenz atomaren orbitale Co, erzeugen wir eine MO-Diagramm für den Übergang Metall komplexe, in Abbildung 3dargestellt. Beachten Sie, dass die übrigen d-orbitale (dXz, dYzund dXy) verwandeln als Set (T2 g) aber haben keine angemessene Symmetrie SALC abgestimmt. Diese atomaren orbitale werden daher "Bonding" MOs. Das heißt, nehmen sie nicht in Verbindung mit den Liganden in diesem Übergang Metall komplexe.
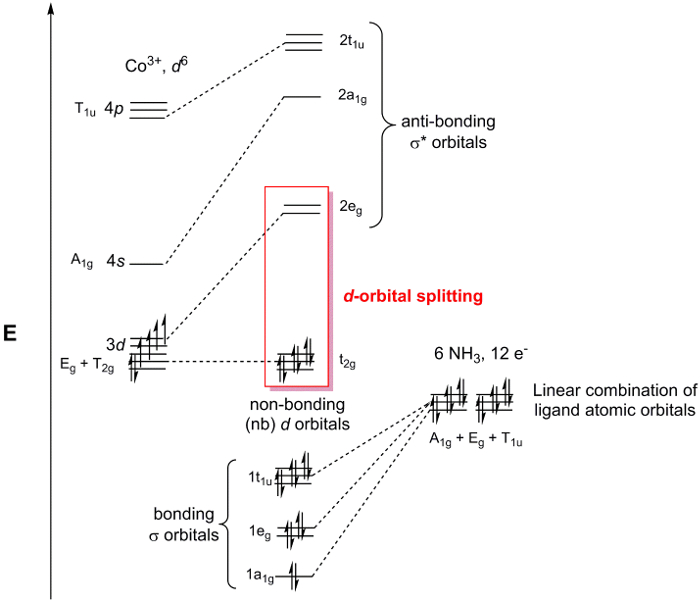
Abbildung 3. MO-Diagramm für [Co (NH3)6] Cl3.
In Abbildung 3 hervorgehoben sind die nicht-Bindung d-orbitale und σ * orbitale mit d-orbital Charakter. Wenn diese Gruppe von MOs separat aus dem gesamten MO-Diagramm gilt es nennt man das d-Orbital-Aufspaltung Diagramm von einem Übergang Metall komplexe. Seit der d-Orbital-Aufspaltung Diagramm enthält die HOMO und LUMO, die in der Regel die wichtigsten orbitale, die Chemie und Spektroskopie der Koordination komplexe zu verstehen sind, Chemiker werden beziehen sich oft auf die d-orbitale Aufteilung Diagramm anstatt das gesamte MO-Diagramm. Bequem, das d-Orbital-Aufspaltung Diagramm kann mit der Anzahl der de– auf dem Metallzentrum gefüllt werden, da die Liganden-basierte Elektronen immer die σ-basierte MOs in der MO-Diagramm füllen.
Unter Berücksichtigung der d -orbital-Aufspaltung Diagramme für M() Dppf) Cl2:
Betrachten Sie einen einfachen 4-Koordinate Metall komplexe MX4. MX-4 kann gibt es in zwei Geometrien: Tetraeder oder quadratisch planar. Die d-orbitale aufteilen Diagramme für der Punkt Td (Tetraeder Gruppen) und D4 h (quadratisch planar) ist in Abbildung 4dargestellt. Während die allgemeine Metallkomplexe M (Dppf) Cl2 keinen 4 gleichwertige Liganden und sind daher nicht in den Punkt Gruppen Td oder D4 h, wir können immer noch diese d-Orbital-Aufspaltung Diagramme als ein Modell zu beschreiben, die d -orbitale MOs für zwei möglichen Geometrien.
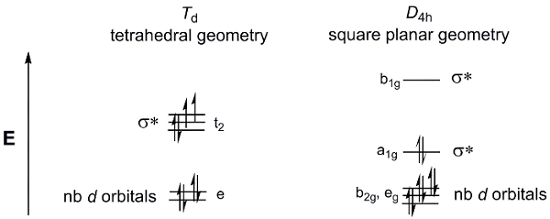
Abbildung 4. Das d-Orbital-Aufspaltung Diagramme für den Punkt Gruppen Td (Tetraeder) und D4 h (quadratisch planar).
Betrachten Sie nun die d-Elektronen Graf m (Dppf) Cl2. Ni und Pd sind in Gruppe 10 des Periodensystems. Daher, sie beide haben die gleiche Oxidationsstufe (2 +) und d-Elektron Graf (d-8). Wenn wir die beiden d füllen-orbitale aufteilen Diagramme oben mit 8 Elektronen, sehen wir, dass die quadratisch planare Geometrie in einem diamagnetischen Komplex führt, während das Tetraeder MO-Diagramm mit einer paramagnetischen Arten übereinstimmt. Es gibt mehrere Faktoren, die in der Bestimmung der Geometrie energetisch begünstigt wird. In quadratisch planare Geometrie gibt es weniger Elektronen in orbitalen Anti-Verklebung, die darauf hinweisen würden, dass die quadratisch planare Geometrie mehr elektronisch begünstigt ist. Wir müssen jedoch auch die notwendige Energie zum paar Elektronen zu betrachten. Das Elektron Energie in quadratisch planare Moleküle Paarung ist höher als die in tetraedrischen Moleküle, die weniger vollständig gefüllte orbitale haben. Schließlich müssen wir den Betrag prüfen, σ * d-orbitale sind destabilisiert. Größere Metallatome haben größere räumliche Überschneidungen mit Liganden, was zu höheren Energie σ * d-orbitale.
Schließlich müssen wir auch den Energiebeitrag von sterischen Abstoßungen zu betrachten. Tetraedrische Geometrie ist mehr sterisch begünstigt (mit Winkel von 109,5 °) im Vergleich zu quadratisch planare Geometrie (90°). Daher gibt es mehrere gegnerische Faktoren, die beeinflussen, welche Geometrie mehr begünstigt, ist die Identität von M in M (Dppf) Cl2gegeben.
Zwischen diesen beiden Geometrien mittels NMR unterscheiden können. Wenn das Molekül quadratisch planar ist, beobachten wir eine Diagnose 1H NMR von einerdiamagnetische Arten. Wenn das Molekül Tetraeder ist, beobachten wir paramagnetische Signale in 1H NMR. Schließlich verwenden wir die Evans-Methode (siehe "Evans Methode" Video für weitere Details) Lösung magnetisches Moment der paramagnetischen Arten zu bestimmen.
Verfahren
Hinweis: Für Sicherheitshinweise, sollte die Schlenk Linie Sicherheit überprüft werden vor der Durchführung der Experimente. Gläser sollten für Sterne Risse vor der Verwendung überprüft werden. Darauf sollte geachtet werden, um sicherzustellen, dass O2 ist nicht in der Schlenk Linie Falle kondensiert, wenn Flüssigkeit N2verwenden. Bei N2 Flüssigkeitstemperatur O2 kondensiert und explosiv in Anwesenheit von organischen Lösungsmitteln. Wenn der Verdacht besteht, dass O2 verdichtet worden oder eine blaue Flüssigkeit in die Kühlfalle eingehalten wird, lassen Sie die Falle unter dynamischen Vakuum kalt. NICHT entfernen Sie die Flüssigkeit N2 Falle oder deaktivieren Sie die Vakuumpumpe. Im Laufe der Zeit verdunstet die Flüssigkeit O2 in die Pumpe; Es ist nur sicher, die flüssige N2 Falle zu entfernen, sobald alle O2 verdampft. Weitere Informationen finden Sie im "Synthese einer Ti(III) Metallocen-Katalysatoren mit Schlenk Linie Technik"-Video. 1
1. Setup der Schlenk-Linie für die Synthese von Ni (Dppf) Cl2 und Pd (Dppf) Cl2
Hinweis: Für eine detailliertere Verfahren, lesen Sie bitte die "Schlenk Linien übertragen von Lösungsmittel" Video der Serie Essentials of Organic Chemistry ).
- Schließen Sie das Überdruckventil.
- Aktivieren Sie das N2 Gas und die Vakuumpumpe.
- Als die Schlenk Linie Vakuum erreicht seine Mindestdruck, bereiten die Kühlfalle mit Flüssigkeit N2 oder Trockeneis/Aceton.
- Montieren Sie die Kühlfalle.
2. Synthese von Ni (Dppf) Cl2 (Abbildung 5) anaerob/inerten Bedingungen
Hinweis während die Synthese von Ni (Dppf) Cl2 in aeroben Bedingungen durchgeführt werden kann, werden höhere Erträge erzielt, wenn unter anaeroben Bedingungen durchgeführt.
- Ein drei-Hals-Kolben Dppf 550 mg (1 Mmol) und 40 mL Isopropanol hinzufügen.
Hinweis: Dppf kann von Sigma-Aldrich erworben werden oder synthetisiert, mit Methoden, die in der Literatur gefunden. 2 - Passen Sie die Mitte Hals von der drei-Hals-Kolben mit einem Kondensator und einem Vakuum-Adapter. Passen Sie die zwei verbleibenden Hälse mit 1 Glasstopfen und 1 Gummiseptum.
- Entgasen der Lösung von sprudelnden N2 Gas durch das Lösungsmittel für 15 min. Einsatz der Vakuumadapter an der Spitze des Kondensators als "Vent".
- Verbinden Sie die Vakuumadapter an der Spitze des Kondensators mit N2 unter Verwendung der Schlenk-Linie.
- Beginn den drei-Hals-Kolben in einem Wasserbad, eingestellt auf 90 ° c erhitzen
- Fügen Sie in einer einzigen Hals Runde untere Kolben 237 mg NiCl2·6H2O(1 Mmol) bis 4 mL einer 2:1-Mischung von Isopropanol (Reagenz Klasse) und Methanol (Reagenz Klasse). Beschallen Sie die resultierende Mischung, bis alle Ni-Salz aufgelöst hat (ca. 1 min).
Hinweis: Wenn ein Sonikator nicht verfügbar ist, erhitzen Sie die Mischung in einem Wasserbad. - Entgasen Sie die Ni-Lösung von sprudelnden N2 Gas durch die Mischung für 5 min.
- Der drei-Hals Rundboden Kolben per Kanüle NiCl2·6H2O Lösung hinzufügen.
- Ermöglichen Sie die Reaktion zum Rückfluss für 2 h bei 90 ° C.
- Lassen Sie die Reaktion im Eisbad abkühlen. Isolieren Sie den daraus resultierende grüne Niederschlag durch Vakuumfiltration durch einen fritted Trichter.
- Waschen Sie das Produkt mit 10 mL kaltem Isopropanol, gefolgt von 10 mL Hexanes.
- Lassen Sie das Produkt an der Luft trocknen, bevor die Vorbereitung der NMR-Probe.
- Nehmen Sie eine 1H NMR des Produkts in Chloroform -d.
- Wenn die 1H NMR ist bezeichnend für eine paramagnetische Spezies ein NMR für die Evans-Methode, gemäß den Anweisungen in Schritt 4 vorbereiten.

Abbildung 5. Synthese von Ni (Dppf) Cl2.
3. Synthese von Pd (Dppf) Cl2 (Abbildung 6)1
Hinweis: Verwenden Sie standard Schlenk-Linie-Techniken für die Synthese von Pd (Dppf) Cl2 (siehe Video "Synthese einer Ti(III) Metallocen-Katalysatoren mit Schlenk Linie Technik").
Hinweis während die Synthese von Pd (Dppf) Cl2 in aeroben Bedingungen durchgeführt werden kann, werden höhere Erträge erzielt, wenn unter anaeroben Bedingungen durchgeführt.
- Schlenk-Kolben 550 mg (1 Mmol) Dppf und 383 mg (1 Mmol) bis(benzonitrile)palladium(II) Chlorid hinzu und die Kanüle Übertragung des Lösungsmittels bereiten Sie Schlenk-Kolben vor.
- Schlenk-Kolben per Kanüle 20 mL Toluol entgast hinzufügen.
- Lassen Sie die Reaktion für mindestens 12 h bei Raumtemperatur gerührt.
- Isolieren Sie den daraus resultierende orangenen Niederschlag durch Vakuumfiltration durch einen fritted Trichter.
- Waschen Sie das Produkt mit Toluol (10 mL), gefolgt von Hexanes (10 mL).
- Lassen Sie das Produkt an der Luft trocknen, bevor die Vorbereitung der NMR-Probe.
- Nehmen Sie eine 1H NMR des Produkts in Chloroform -d.
- Wenn 1H NMR bezeichnend für eine paramagnetische Spezies ist, bereiten Sie ein NMR für die Evans-Methode folgen Sie den Anweisungen in Schritt 4 beschrieben.

Abbildung 6. Synthese von Pd (Dppf) Cl2.
4. Vorbereitung der Evans Methode Probe
Hinweis: Für eine detailliertere Verfahren finden Sie "Evans-Methode"-Video.
- In einer Durchstechflasche funkeln bereiten die 50: 1 (Volumen: Volumen) Lösung von Chloroform -d: Trifluorotoluene. Pipette 2 mL deuterierte Lösungsmittel und dazu fügen 40 µL des Trifluorotoluene. Verschließen Sie das Fläschchen.
Hinweis: In diesem Beispiel 19F NMR verwenden wir werden um die Verschiebung des Signals F im Trifluorotoluene im Beisein der paramagnetischen Arten beobachten. - Bereiten Sie mit dieser Lösung die Kapillare einfügen.
- Wiegen Sie 10-15 mg der paramagnetischen Probe in ein neues Fläschchen funkeln und beachten Sie die Masse.
- Pipette ~ 600 µL bereit Lösungsmittelgemisches in das Fläschchen mit der paramagnetischen Arten. Beachten Sie die Masse. Stellen Sie sicher, dass die solide vollständig auflöst.
- Ein standard NMR-Röhrchen sorgfältig Rückgang der Kapillare einfügen in einem Winkel, um sicherzustellen, dass es nicht brechen.
- Die Lösung mit der paramagnetischen Spezies in der NMR-Röhrchen Pipette.
- Erwerben Sie und speichern Sie eine standard 19-F-NMR-Spektrum.
- Beachten Sie die Temperatur der Sonde.
- Beachten Sie die Radiofrequenz.
Ergebnisse
Pd (Dppf) Cl2:
1 H-NMR (Chloroform -d, 400 MHz, δ, ppm): 4.22 (Alpha-H), 4.42 (Beta-H), 7.89 7,44, 7.54 (aromatische)3.
NI (Dppf) Cl2:
1 H-NMR (Chloroform -d, 300 MHz, δ, ppm): 20,85, 10.04, 4.23, 3,98, 1,52,-3.31,-7.10.
Evans Methode, Blick auf die 19F-Verschiebung des Trifluorotoluene:
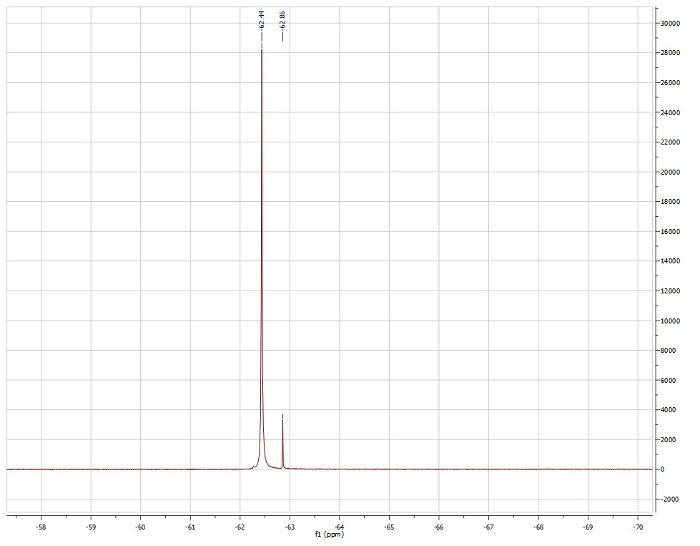
BeobachtetenµEff = 3,15 µb
Masse der Probe: 9,5 mg
Masse der Lösung (Chloroform -d + Trifluorotoluene): 0,8365 g
Temperatur der Sonde: 296,3 K
NMR-Feld (MHz): 470.06
Berichtet µEff = 3,39 µb. 4
Für S = 1 (vorhergesagten basierend auf tetraedrische Geometrie, Abbildung 4), theoretische µEff = 2,83 µb.
Für S = 3/2, theoretische µEff = 3,46 µb.
Basierend auf der 1H-NMR-Daten, sehen wir, dass Pd (Dppf) Cl2 diamagnetisch ist und daher quadratisch planare Geometrie weist. 1H NMR Ni (Dppf) Cl2 ist paramagnetisch und ist daher in der Ni-Mitte Tetraeder. Evans Methode bestätigt, dass Ni (Dppf) Cl2 ist paramagnetisch, präsentiert einen Lösung magnetisches Moment von 3,15 µb, das nah an die Literatur berichteten Wert für diese Verbindung. Da Ni gering ist, überwiegt der Sterics elektronische Stabilisierung quadratisch planare Geometrie machen Ni (Dppf) Cl2 tetraedrischen zugeordnet. Auf der anderen Seite die Pd ist groß und hat daher höhere Energie σ * d-orbitale. In diesem Fall überwiegt die elektronische Stabilisierung erheblich die sterischen Abstoßungen, wodurch eine quadratisch planare Geometrie bei Pd PD (Dppf) Cl2.
Anwendung und Zusammenfassung
Dieses Video demonstriert, wie MO-Theorie als ein Modell der Bindung in Übergang Metall komplexe genutzt werden kann. Wir synthetisiert zwei komplexe mit der allgemeinen Formel M (Dppf) Cl2. Wenn M = Ni, die 4-Koordinate komplexen Exponate eine tetraedrische Geometrie. Ersetzen die Ni-Atom mit einem größeren Übergangsmetall (Pd), nimmt das Molekül quadratisch planare Geometrie.
Zuvor lernten wir viel über die wichtige Rolle Ferrocen spielt auf dem Gebiet der metallorganischen Chemie. Substituierte Ferrocenes, einschließlich Dppf, dienen als chelatisierenden Liganden für 1St, 2Ndund 3rd Zeile Übergangsmetalle. Die daraus resultierende komplexe dienen in der homogenen Katalyse (i.e., [1,1'-bis(diphenylphosphino)ferrocene]palladium(II) Paraquatdichlorid, Pd (Dppf) Cl2, ist ein Katalysator für C-C- und C-Heteroatom-Bindung bilden Reaktionen).
Die Verklebung in Übergang Metall komplexe Verständnis ist wichtig für die Erklärung ihrer Struktur und Reaktivität. Eine der Stärken der MO-Theorie ist, dass sie ein gutes Modell, das verwendet werden kann enthält, zu erklären, die Reaktivität der Übergang Metall komplexe. In vielen Fällen befindet sich das Metallzentrum Reaktivität, ausgestellt durch das Molekül. Daher ist es wertvoll, um ein Bild von der Elektronendichte an das Metallzentrum, die im d -orbital splitting Diagramm abgeleitet von der MO-Theorie (Abbildung 3) zusammengefasst werden. Beachten Sie, die nicht nur, dass die MOs in der d-orbitale aufteilen Diagramm zeigen meist d-orbital Charakter (σ *-orbitale sind in Energie, die atomare dam nächsten-orbitalen des Metalls und somit ein Großteil der Elektronendichte in die MOs ist zentriert auf das Metallatom), aber auch das splitting Diagramm enthält die HOMO und LUMO des Moleküls. Daher keine Chemie, das auftritt, hat direkte Auswirkung auf das d-Orbital-Aufspaltung Diagramm des Moleküls.
Referenzen
- Corain, B., Longato, B., Favero, G. Heteropolymetallic Complexes of 1,1’-Bis(diphenylphosphino)ferrocene (dppf). III*. Comparative Physicochemical Properties of (dppf)MCl2 (M = Co, Ni, Pd, Pt, Zn, Cd, Hg). Inorg Chim Acta. 157, 259-266 (1989).
- Cullen, W. R., Einstein, F. W. B., Jones, T., Kim, T.-J. Structures of three hydrogenation catalysts [(P-P)Rh(NBD)]ClO4 and some comparative rate studies where (P-P) = (η5-R1R2PC5H4)(η5-R3R4PC5H4)Fe (R1 = R2 = R3 = R4 = Ph, R1 = R2 = Ph, R3 = R4 = CMe3, R1 = R3 = Ph, R2 = R4 = CMe3). Organometallics. 4(2), 346-351 (1983).
- Colacot, T. J., C.-Olivares, R., H.-Ortega, S. Synthesis, X-ray, spectroscopic and a preliminary Suzuki coupling screening studies of a complete series of dppfMX2 (M = Pt, Pd, X = Cl, Br, I). J Organomet Chem. 637-639, 691-697 (2001).
- Rudie, A. W., Lichtenberg, D. W., Katcher, M. L., Davison, A. Comparative Study of 1,1’-bis(diphenylphosphino)cobaltocinium hexafluorophosphate and 1,1’-bis(dipenylphosphino)ferrocene as Bidentate Ligands. Inorg Chem. 17(10), 2859-2863, 1978.
pringen zu...
Videos aus dieser Sammlung:

Now Playing
Molekülorbital (MO)-Theorie
Inorganic Chemistry
35.1K Ansichten

Synthese eines Ti(III)-Metallocen-Katalysators mittels Schlenk-Technik
Inorganic Chemistry
31.5K Ansichten

Handschuhbox und Verunreinigungssensoren
Inorganic Chemistry
18.6K Ansichten

Reinigung von Ferrocen durch Sublimation
Inorganic Chemistry
54.3K Ansichten

Die Evans-Methode
Inorganic Chemistry
67.9K Ansichten

Einkristall- und Pulverröntgendiffraktometrie
Inorganic Chemistry
103.9K Ansichten

Elektronenparamagnetische Rezonanzspektroskopie (EPR-Spektroskopie)
Inorganic Chemistry
25.3K Ansichten

Mößbauerspektroskopie
Inorganic Chemistry
21.9K Ansichten

Lewis-Säure-Base-Wechselwirkungen in Ph3P-BH3
Inorganic Chemistry
38.7K Ansichten

Struktur von Ferrocen
Inorganic Chemistry
79.1K Ansichten

Anwendung der Gruppentheorie auf die IR-Spektroskopie
Inorganic Chemistry
44.9K Ansichten

Vierfach-metallgeklebte Schaufelräder
Inorganic Chemistry
15.3K Ansichten

Farbstoffsensibilisierte Solarzellen
Inorganic Chemistry
15.7K Ansichten

Synthese eines Sauerstoff-transportierenden Cobalt(II) - Komplex
Inorganic Chemistry
51.5K Ansichten

Photochemische Initiierung von radikalischen Polymerisationsreaktionen
Inorganic Chemistry
16.7K Ansichten
Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten