경사 플레이트 대상 제트 충돌
Overview
출처: 리카르도 메지아 알바레즈와 후삼 히크마트 자바, 기계 공학과, 미시간 주립 대학, 이스트 랜싱, MI
이 실험의 목표는 유체 흐름이 동적 압력을 정적 압력으로 변환하여 구조에 힘을 미치는 방법을 보여주는 것입니다. 이를 위해, 우리는 평면 제트가 평평한 접시에 충돌하고 플레이트를 따라 결과 압력 분포를 측정합니다. 결과 력은 플레이트 표면을 따라 압력 분포와 적절하게 정의된 영역 차이 사이에 제품을 통합하여 추정됩니다. 이 실험은 제트의 방향과 두 개의 유량에 대하여 플레이트의 경사의 두 각도에 대해 반복됩니다. 각 구성은 플레이트를 따라 다른 압력 분포를 생성하며, 이는 플레이트 표면의 정적 압력으로 동적 압력을 변환하는 다양한 수준의 결과입니다.
이 실험을 위해 스캐닝 밸브에 연결된 다이어프램 압력 변환기로 압력을 측정합니다. 플레이트 자체는 호스를 통해 스캐닝 밸브에 연결하는 압력 탭이라는 작은 천포가 있습니다. 스캐닝 밸브는 이러한 탭에서 압력 변환기로 한 번에 하나씩 전송합니다. 압력은 압력 변환기가 전압으로 변환되는 다이어프램에 기계적 편향을 유도합니다. 이 전압은 다이어프램의 양면 사이의 압력 차이에 비례합니다.
Principles
중력 잠재력의 무시할 수 없는 변화와 함께 꾸준히 비압축성 흐름에서 베르누이의 방정식은 운동 에너지와 압력 잠재적 에너지라는 두 가지 형태의 에너지가 추가된 것으로 해석될 수 있습니다. 비효율적인 공정에서 이러한 형태의 에너지는 초기 총 에너지량을 일정하게 유지하면서 유선형을 따라 자유롭게 서로 변신할 수 있습니다. 이 에너지 합계는 베르누이의 상수라고 합니다. 편의를 위해 베르누이의 방정식은 치수 균질성의 원리를 사용하여 압력치로 표현될 수 있다[3]. 이러한 차원 변환에 따라 운동 에너지와 관련된 용어는 "동적 압력"이라고 불리며 압력 잠재적 에너지와 관련된 용어는 "정적 압력"이라고 하며 Bernoulli의 상수는 "침체 압력"이라고 명명됩니다. 후자는 모든 동적 압력을 정적 압력으로 변환하여 흐름이 중단될 경우 도달하는 최대 압력으로 해석될 수 있습니다. 이러한 원리들은 다음과 같은 형태의 베르누렐리 방정식에 의해 더 잘 설명할 수 있습니다.
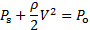 (1)
(1)
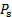 정적 압력은
정적 압력은  동적 압력이며 침체
동적 압력이며 침체  압력입니다. 도 1(A)은 현재 실험의 회로도를 나타낸다. 그림과 같이, 에어 제트는 폭 W의 슬릿을 통해 고압 plenum에서 출구와 수신기라는 낮은 압력에서 밀폐 된 공간으로 L을 스팬. 수신기는 실험의 테스트 섹션 역할을 하는 작은 방입니다. 데이터 수집 장비와 실험가가 있습니다. 몇 거리 동안 흐르면 제트는 제트 축으로 각도를 만드는 수신기 내부의 평평한 플레이트에 충돌합니다. 그림 1(A)의 제트기는 세 개의 유선형으로 설명되어 있습니다. 중간 유선형은 두 지역에서 제트기를 나눕니다. 분할 유선형이 편향되지 않기 때문에 침체 지점으로 알려진 벽에서 바로 멈춥니다. 이 시점에서 모든 동적 압력이 정적 압력으로 변환되고 압력이 최대 수준에
압력입니다. 도 1(A)은 현재 실험의 회로도를 나타낸다. 그림과 같이, 에어 제트는 폭 W의 슬릿을 통해 고압 plenum에서 출구와 수신기라는 낮은 압력에서 밀폐 된 공간으로 L을 스팬. 수신기는 실험의 테스트 섹션 역할을 하는 작은 방입니다. 데이터 수집 장비와 실험가가 있습니다. 몇 거리 동안 흐르면 제트는 제트 축으로 각도를 만드는 수신기 내부의 평평한 플레이트에 충돌합니다. 그림 1(A)의 제트기는 세 개의 유선형으로 설명되어 있습니다. 중간 유선형은 두 지역에서 제트기를 나눕니다. 분할 유선형이 편향되지 않기 때문에 침체 지점으로 알려진 벽에서 바로 멈춥니다. 이 시점에서 모든 동적 압력이 정적 압력으로 변환되고 압력이 최대 수준에  도달합니다. 점진적으로 덜 동적 압력이 정적 압력으로 변환되므로 압력 레벨이 침체 지점에서 멀리 감소합니다.
도달합니다. 점진적으로 덜 동적 압력이 정적 압력으로 변환되므로 압력 레벨이 침체 지점에서 멀리 감소합니다.
충돌 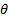 각도(그림 1)에 따라, 침체 유선형은 다른 경로를 따릅니다.
각도(그림 1)에 따라, 침체 유선형은 다른 경로를 따릅니다.  때, 제트기의 중심선도 침체가 유선형입니다. 감소함에 따라
때, 제트기의 중심선도 침체가 유선형입니다. 감소함에 따라 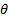 침체 유선형은 제트기의 중심선에서 제트기의 바깥쪽 가장자리에 더 가깝게 시작하는 궤도로 이동합니다. 90o는 최대 속도, ergo 최대 동적 압력의 궤적이기 때문에 그 결과 침체 점은 더 작은 값에서 다른 궤적에 비해 압력의 최대 값에
침체 유선형은 제트기의 중심선에서 제트기의 바깥쪽 가장자리에 더 가깝게 시작하는 궤도로 이동합니다. 90o는 최대 속도, ergo 최대 동적 압력의 궤적이기 때문에 그 결과 침체 점은 더 작은 값에서 다른 궤적에 비해 압력의 최대 값에 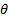 도달합니다. 요약하면, 압력 프로파일에 대한 충돌 각도의 효과는 최대 값을 줄이고 제트 출구에 가까운 플레이트 영역으로 피크를 대체하는 것입니다.
도달합니다. 요약하면, 압력 프로파일에 대한 충돌 각도의 효과는 최대 값을 줄이고 제트 출구에 가까운 플레이트 영역으로 피크를 대체하는 것입니다.
도 1(A)의 파선선은 제트에 노출된 플레이트의 표면을 따라 그물 압력 분포를 나타낸다. 도 1(B)에서 플레이트의 총 압력이 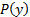 주변 압력, 플러스 충돌
주변 압력, 플러스 충돌 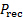 압력 또는 과압의 첨가,
압력 또는 과압의 첨가, 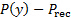 . 주변 압력이 균질적으로 분포되기 때문에 플레이트의 하중이 엄격히 과압의 결과입니다. 이 압력 분포는 실험적으로 결정되고 다음 일체형에 따라 플레이트의 순 부하를 추정하는 데 사용됩니다.
. 주변 압력이 균질적으로 분포되기 때문에 플레이트의 하중이 엄격히 과압의 결과입니다. 이 압력 분포는 실험적으로 결정되고 다음 일체형에 따라 플레이트의 순 부하를 추정하는 데 사용됩니다.
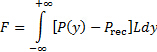 (2)
(2)
실험 데이터는 이산이므로 사다리꼴 규칙 또는 심슨 규칙 [4]을 사용하여 이 일체형을 추정할 수 있습니다.
또한, 유체가 고압 지역에서 오리피스 또는 슬릿을 통해 저압 영역으로 배출되는 경우, 발행 제트는 처음에는 베나 수축기(참조그림 1 참조)라고 불리는 지역으로 수렴한 다음 배출 포트에서 멀리 흐면서 갈라지는 경향이 있다. 베나 수축은 사실 제트기가 유선형이 평행해지는 방전 항구를 떠난 후 첫 번째 위치입니다. 따라서 이것은 정적 압력이 주변의 압력과 동일한 제트기를 따라 첫 번째 장소입니다 [5]. 본 실험에서, plenum은 고압 영역이고 수신기는 저압 영역이다. 또한, plenum 내부의 속도는 무시할 수 있으며 매우 양호한 근사치로 정체된 것으로 간주될 수 있습니다. 따라서, 방정식 (1)은 다음과 같이 베나 계약의속도를 결정하는 데 사용될 수있다 :
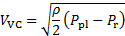 (3)
(3)
여기서,  플레넘과 수신기 사이의 압력 차이입니다. 일반적으로 슬릿 폭과 베나 수축 사이의 수축 비율은 매우 약 [5, 6, 7]입니다.
플레넘과 수신기 사이의 압력 차이입니다. 일반적으로 슬릿 폭과 베나 수축 사이의 수축 비율은 매우 약 [5, 6, 7]입니다.
 (4)
(4)
따라서 질량 유량은 다음과 같이 (3) 및 (4)에서 추정될 수 있습니다.
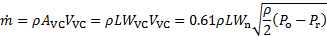 (5)
(5)
여기,  베나 수축의 영역입니다.
베나 수축의 영역입니다.

그림 1. 기본 구성의 회로도. 비행기 제트는 폭 W의 슬릿을 통해 수신기에 plenum을 종료합니다. 제트는 경사 판에 충돌하고 표면에 압력 부하를 가하는 동안 편향됩니다 (대시 라인). 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
Procedure
1. 시설 설정
- 시설에 흐름이 없는지 확인합니다.
- 도 2의 회로도에 따라 계측기를 설정합니다.
- 플레이트를 원하는 각도로
 조정합니다. 이 값을 표 1에 기록합니다.
조정합니다. 이 값을 표 1에 기록합니다. - 제트 노즐 너비 를 측정W. 표 1에서 이 값을 기록합니다.
- 표 1에서 이 값을 기록하는 플레이트 스팬 L. 레코드를 측정합니다.
- 압력 변환기0.
- 압력 변환기, m p(Pa/V)의 교정 상수를 기록합니다. 이 값을 표 1에 기록합니다.
- 변환기의 고압 포트(+로 표시됨)를 plenum의 압력 탭(로
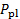 표시됨)에 연결합니다.
표시됨)에 연결합니다. - 모든 작업이 수신기 내부에서 이루어지기 때문에 트랜스듀서(-로 표시)의 저압 포트를 열어 수신기()의 압력을
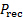 감지합니다.
감지합니다. - 플로우 시설(FLL)을 시작합니다.
- 디지털 멀티미터를 사용하여 압력
 변환기에서 감지된 플넘과 수신기 사이의 압력 차이와 관련된 전압(V)을 기록합니다. 이 값을 표 2에 기록합니다.
변환기에서 감지된 플넘과 수신기 사이의 압력 차이와 관련된 전압(V)을 기록합니다. 이 값을 표 2에 기록합니다. - 1.7에서 교정 상수 mp를 사용하여 plenum과 수신기 ()의 압력 차이를
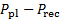 결정합니다. 표 2에 이 값을 기록합니다.
결정합니다. 표 2에 이 값을 기록합니다.

그림 2 . 데이터 수집 시스템의 세부 정보. 장비 연결에 대한 회로도. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
표 1 . 실험 연구를 위한 기본 매개 변수입니다.
| 매개 변수 | 값 |
| 제트 노즐 폭(Wn) | 41.3 mm |
| 플레이트 스팬(L) | 81.3 cm |
| 플레이트 높이(H) | 61cm |
| 트랜스듀서 교정 상수(m_p) | 137.6832 Pa/V |
2. 실험 실행
- 트랜스듀서의 고압 포트(+로 표시)를 스캐닝 밸브의 공통 포트에 연결합니다. 수신기()의 압력을 감지하기 위해 트랜스듀서(-로 표시)의 저압 포트를 열어
 둡니다.
둡니다. - 첫 번째 압력 탭 위치에서 측정을 시작하기 위해 스캐닝 밸브를 홈으로 홈으로 유지합니다.
- 트래버스 VI(LabView 가상 계측기)를 실행합니다.
- VI에서 교정 상수 mp를 입력합니다.
- 샘플링 속도를 100Hz로 설정하고 총 샘플(예: 5초 의 데이터)을 설정합니다.
 플레이트 압력 데이터를 획득하는 압력 탭의 VI 위치()를 입력합니다. 압력 탭이 25.4mm 간격을 두는 것을 고려하십시오. 따라서 위치는
플레이트 압력 데이터를 획득하는 압력 탭의 VI 위치()를 입력합니다. 압력 탭이 25.4mm 간격을 두는 것을 고려하십시오. 따라서 위치는  mm이 되며
mm이 되며 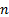 탭 의 인덱스는 0에서 시작합니다.
탭 의 인덱스는 0에서 시작합니다.- 데이터를 기록합니다. VI는 압력 탭과 수신기 사이의 압력 차이를 읽습니다
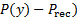 (.
(. - 스캔 밸브를 다음 탭 위치로 단계별로 단계별로 이동합니다.
- 모든 압력 탭이 통과될 때까지 2.6에서 2.8단계를 반복합니다.
- 끝에서 VI는 테이블과 탭 위치 대 압력의 플롯을 제공합니다.
- VI를 중지합니다.
- 흐름 제어 판의 위치를 변경하여 흐름 영역을 대략 절반으로 닫습니다(참조그림 3 참조). 이렇게 하면 유량이 수정됩니다. 방정식(5)을 사용하여 이 유량의 값을 결정합니다.
- 흐름 제어 플레이트의 새로운 위치에 대해 2.3 ~ 2.11 단계를 반복합니다.
- 충돌 플레이트의 각도를 수정하고 유동 제어 판을 초기 위치로 설정합니다.
- 반복 단계 2.3 받는 일 2.14 에 대 한 80o,70o,60o,50o,그리고 45o.

그림 3 . 실험 설정. 테스트 섹션입니다. 왼쪽: 슬릿 앞의 충돌 플레이트. 고압 공기는 이 슬릿을 통해 플넘에서 수신기로 배출됩니다. 중간: 충돌 판에 연결된 압력 탭은 한 번에 하나씩 샘플링하기 위해 스캐닝 밸브에 배분됩니다. 오른쪽: 수신기 방전 앞의 충돌 플레이트. 방전은 유량을 조절하기 위한 천대판이 있다. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
3. 분석
- 각 경사도 에 대해 두 유량에 대한 압력 데이터를 플롯합니다.
- 실험 데이터를 사용하여 방정식(2)을 기반으로 플레이트의 힘을 추정합니다.
- 방정식(3)을 사용하여 베나 수축기에서 제트 속도를 결정합니다.
- 방정식(5)을 사용하여 질량 유량을 추정합니다.
Results
도 4는 두 개의 서로 다른 각도와 두 개의 서로 다른 유량으로 플레이트에 충돌하는 비행기 제트에 대해 얻은 4세트의 결과를 보여줍니다. 실제로 트랜스듀서의 저압 면이 수신기에 열리기 때문에 그 판독값은 실제로 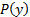 도 4에표시된 점인 과압에만 해당합니다.
도 4에표시된 점인 과압에만 해당합니다.
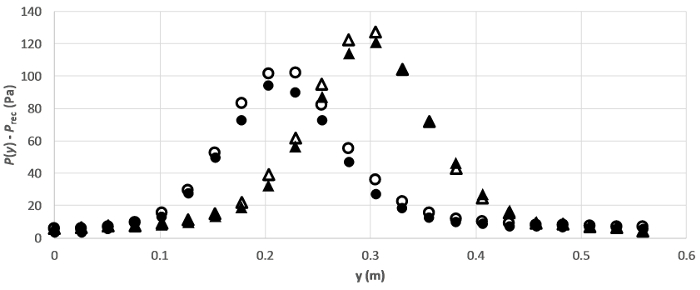
그림 4. 대표적인 결과. 플레이트를 따라 압력 분포를 두 각도와 두 개의 유량에 대 한. 기호는 : 
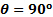 : , m /
: , m / 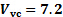 s;
s;  :
: 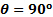 ,
,  m/s;
m/s;  :
:  ,
, 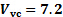 m/s;
m/s;  :
:  ,
,  m/s.
m/s.
그림 4에따르면, 90o 장애에 대한 프로파일은 70o 장애에 대한 프로파일보다 높습니다. 이 동작의 이유는 이전 케이스에 대한 침체 가 유선형이 흐름 중심선, 즉 피크 속도에 대한 간소화와 결과적으로 최대 동적 압력에 해당하기 때문입니다. 침체유선형은 피크 속도 선에서 멀어지고 충돌 각도가 감소함에 따라 원래 경로에서 구부러지며 구부러지게 됩니다. 이 효과는 도 1(A)에 스케치되며 압력 프로파일의 피크 압력이 플레이트의 중심에서 멀어지는 이유이기도 합니다.
예상대로, 최대 압력은 유량(그림 4의 폐쇄 심볼)으로 감소하므로 운동 에너지의 일반적인 감소가 있기 때문에 유량이 감소함에 따라 동적 압력이 감소합니다. 이 최대 압력은 사실 침체 압력의  척도이며, 이전에 설명했습니다. 90o에서플레이트를 충돌하는 제트기의 경우
척도이며, 이전에 설명했습니다. 90o에서플레이트를 충돌하는 제트기의 경우  압력 탭이 중심선과 일치하기 때문에 정확한 측정값이며, 침체가 유선형인 제트의 경계선과 일치하기 때문입니다. 그러나 그림 1a에서 제안 했듯이, 정체는 충돌 각도가 감소함에 따라 원래 경로에서 멀리 구부러지며. 이 새로운 조건하에서, 이 간소화가 충돌 위치에 있는 압력 탭과 정확하게 일치한다는 것을 보장하지 않습니다. 따라서90o와 다른 충돌 각도에서 관찰된 피크 압력은 근사치에
압력 탭이 중심선과 일치하기 때문에 정확한 측정값이며, 침체가 유선형인 제트의 경계선과 일치하기 때문입니다. 그러나 그림 1a에서 제안 했듯이, 정체는 충돌 각도가 감소함에 따라 원래 경로에서 멀리 구부러지며. 이 새로운 조건하에서, 이 간소화가 충돌 위치에 있는 압력 탭과 정확하게 일치한다는 것을 보장하지 않습니다. 따라서90o와 다른 충돌 각도에서 관찰된 피크 압력은 근사치에  불과합니다.
불과합니다.
표 2는 두 가지 다른 충돌 각도와 유량에 대한 실험 측정에서 얻은 결과를 보여줍니다.
표 2. 대표적인 결과.
| 매개 변수 | 실행 1 | 실행 2 | 실행 3 | 4실행 |
| 플레이트 각도(θ) | 90o | 90o | 70o | 70o |
| 디지털 멀티 미터 판독 (E) | 2.44 V | 2.33 V | 2.44 V | 2.28 V |
| 압력 차이(P_pl-P_rec) | 335.95 파 | 320.80 파 | 335.95 파 | 313.92 파 |
| 베나 계약에서 속도 (V_VC) | 10.14 m/s | 9.91 m/s | 10.14 m/s | 9.81 m/s |
| 질량 유량(m)을 | 0.254 kg/s | 0.249 kg/s | 0.254 kg/s | 0.246 kg/s |
| 침체 압력 (P_o) | 127.16 파 | 121.19 파 | 101.78 파 | 94.31 파 |
| 플레이트에 적재(F) | 16.84 N | 16.24 N | 14.11 N | 12.32 N |
Application and Summary
본 원에 등장하는 실험은 동적 압력을 정적 압력으로 변환하여 물체에 하중을 생성하는 압력과 속도의 상호 작용을 보여 주었다. 이러한 개념은 두 개의 서로 다른 각도와 두 개의 서로 다른 유량의 평면 플레이트에 충돌하는 비행기 제트로 입증되었습니다. 이 실험은 모든 동적 압력이 정적 압력으로 변환되는 침체 지점에서 하중이 가장 높으며, 역학에서 정적으로 변환하는 수준이 침체 지점에서 떨어진 위치에서 감소함에 따라 그 크기가 감소한다는 것을 명확하게 입증했습니다. 발생 각도는 중앙선(최대) 속도와 일치하는 압력에서 낮은 수준의 동적 압력을 운반하는 간소화된 압력으로 전환하기 때문에 총 부하를 줄이는 효과가 있습니다.
또한 이러한 실험은 압력 탭에서 얻은 데이터를 수치적으로 통합하여 흐름에 노출된 개체의 총 부하를 확인하는 방법을 입증하는 목적으로도 사용되었습니다. 또한, 정적 압력의 역변환을 동적 압력으로 전환하여 제트기의 속도 및 질량 유량을 추정하는 데도 사용되었습니다. 결과적으로 압력과 속도의 상호 작용은 유동 진단에 사용할 수 있습니다.
정적 프로브 - 현재 실험에서 탐구되지 않은 개념은 Pitot에 의해 속도입니다. 이들은 직접 침체와 정압 사이의 차이를 측정하는 프로브입니다, 이는 정확히 기식 (3)에 사용 된 것은 베나 수축기에서속도를 결정하기 위해. 적어도 90o 각도 플레이트에서 중앙 압력 탭이 침체 지점에 직접 노출되어 피토 프로브가 됩니다. 압력 트랜스듀서는 각 압력 탭의 압력을 수신기의 압력과 비교하기 때문에 그 결과는 직접  측정됩니다. 이 측정값을 방정식(3)에서 대체하면, 그 결과는 침체지점에 가깝지만 여전히 영향 반경을 벗어난 침체 유선형에 대한 점의 속도입니다. 이 측정은 침체 유선형에 해당 지점의 정확한 위치를 알 수 없기 때문에이 실험에서 제한된 사용입니다.
측정됩니다. 이 측정값을 방정식(3)에서 대체하면, 그 결과는 침체지점에 가깝지만 여전히 영향 반경을 벗어난 침체 유선형에 대한 점의 속도입니다. 이 측정은 침체 유선형에 해당 지점의 정확한 위치를 알 수 없기 때문에이 실험에서 제한된 사용입니다.
앞서 언급했듯이 압력 측정을 사용하여 유동 속도를 결정할 수 있습니다. 본 명세서에서 설명된 응용 프로그램에서, plenum과 수신기 사이의 압력의 변화는 베나 수축기에서평균 속도를 추정하기에 충분했다. 또한, 부수적으로, 압력 탭은 수식(3)에서 유동 속도를 결정하기 위해 정적 압력을 감지하는 프로브와 함께 사용될 수 있는 피토 튜브(3)(대체). 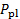


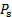 실제로 Pitot 프로브와 Prandtl 튜브로 알려진 정적 프로브를 결합한 단일 장치는 속도를 측정하기 위해 유체 엔지니어링에서 가장 확장된 진단 장치일 수 있습니다. 그림 5에 도시된 바와 같이, 이 프로브는 두 개의 동심관으로 구성됩니다. 내부 튜브는 침체 압력을 감지하는 흐름에 직면하고, 외부 튜브에는 정적 압력을 감지하는 측면 포트 세트가 있습니다. 압력 변환기 또는 액체 컬럼 기압과 같은 센서는 이 두 압력 간의 차이를 결정하기 위해 방정식(3)으로부터의 속도를 추정하는 데 사용됩니다(다시,
실제로 Pitot 프로브와 Prandtl 튜브로 알려진 정적 프로브를 결합한 단일 장치는 속도를 측정하기 위해 유체 엔지니어링에서 가장 확장된 진단 장치일 수 있습니다. 그림 5에 도시된 바와 같이, 이 프로브는 두 개의 동심관으로 구성됩니다. 내부 튜브는 침체 압력을 감지하는 흐름에 직면하고, 외부 튜브에는 정적 압력을 감지하는 측면 포트 세트가 있습니다. 압력 변환기 또는 액체 컬럼 기압과 같은 센서는 이 두 압력 간의 차이를 결정하기 위해 방정식(3)으로부터의 속도를 추정하는 데 사용됩니다(다시, 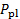
 대체및
대체및  와
와 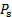 함께). 이와 같은 프로브, 또는 Pitot와 독립적 인 정적 프로브의 조합은 실제로 비행기에 비해 바람의 속도를 결정하기 위해 비행기에서 사용된다.
함께). 이와 같은 프로브, 또는 Pitot와 독립적 인 정적 프로브의 조합은 실제로 비행기에 비해 바람의 속도를 결정하기 위해 비행기에서 사용된다.
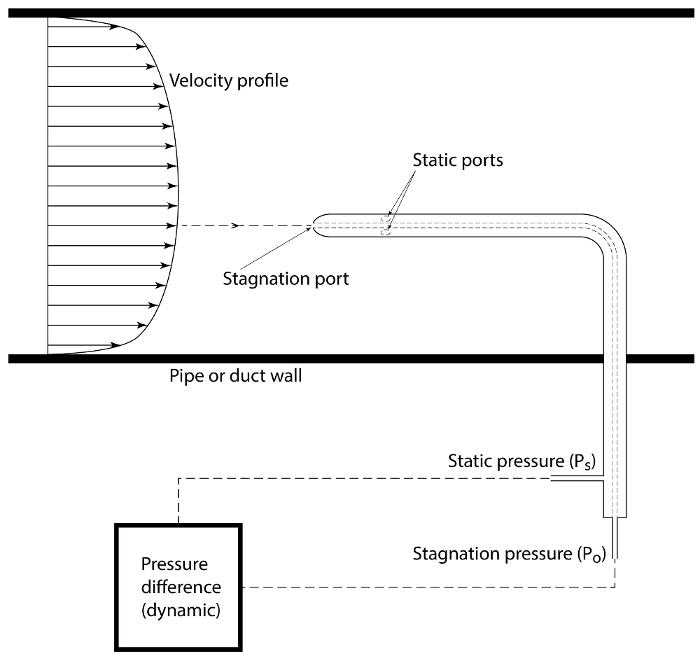
그림 5. 흐름 속도 측정. 피토 정적(또는 Prandtl) 프로브는 동적 압력에 따라 속도 분포를 결정합니다. 이 프로브는 유동 필드를 가로질러 서로 다른 위치에서 속도를 결정합니다. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
Tags
건너뛰기...
이 컬렉션의 비디오:

Now Playing
경사 플레이트 대상 제트 충돌
Mechanical Engineering
10.8K Views

침지된 물체의 부력과 항력
Mechanical Engineering
30.2K Views

플로팅 선박의 안정성
Mechanical Engineering
23.1K Views

추진력과 추력
Mechanical Engineering
22.1K Views

파이프 네트워크 및 압력 손실
Mechanical Engineering
58.7K Views

담금질 및 비등
Mechanical Engineering
8.2K Views

하이드롤릭 점프
Mechanical Engineering
41.3K Views

열교환기 분석
Mechanical Engineering
28.3K Views

냉장 소개
Mechanical Engineering
25.0K Views

열선 풍속 측정
Mechanical Engineering
15.8K Views

난류 측정
Mechanical Engineering
13.6K Views

블러프 바디를 지나는 흐름의 시각화
Mechanical Engineering
12.1K Views

시스템 분석에 대한 에너지 보존적 접근 방식
Mechanical Engineering
7.4K Views

질량 보존 및 유속 측정
Mechanical Engineering
22.9K Views

제어 볼륨 방법을 사용한 평판 충돌력 결정
Mechanical Engineering
26.0K Views
Copyright © 2025 MyJoVE Corporation. 판권 소유