Costanti dei materiali

Fonte: Roberto Leon, Dipartimento di Ingegneria Civile e Ambientale, Virginia Tech, Blacksburg, VA

A differenza della produzione di automobili o tostapane, dove vengono realizzate milioni di copie identiche e sono possibili test approfonditi sui prototipi, ogni struttura di ingegneria civile è unica e molto costosa da riprodurre (Fig.1). Pertanto, gli ingegneri civili devono fare ampio affidamento sulla modellazione analitica per progettare le loro strutture. Questi modelli sono astrazioni semplificate della realtà e vengono utilizzati per verificare che i criteri di prestazione, in particolare quelli relativi alla resistenza e alla rigidità, non vengano violati. Per svolgere questo compito, gli ingegneri richiedono due componenti: (a) un insieme di teorie che spiegano come le strutture rispondono ai carichi, cioè come le forze e le deformazioni sono correlate, e (b) una serie di costanti che differenziano all'interno di tali teorie come i materiali (ad esempio acciaio e calcestruzzo) differiscono nella loro risposta.

Figura 1: Hub di trasporto del World Trade Center (NYC).

La maggior parte dei progetti ingegneristici oggi utilizza principi elastici lineari per calcolare forze e deformazioni nelle strutture. Nella teoria dell'elasticità, sono necessarie diverse costanti materiali per descrivere la relazione tra stress e deformazione. La sollecitazione è definita come la forza per unità di area, mentre la deformazione è definita come la variazione di dimensione quando è sottoposta a una forza divisa per la grandezza originale di tale dimensione. Le due costanti più comuni di queste sono il modulo di elasticità (E), che mette in relazione la sollecitazione con la deformazione, e il rapporto di Poisson (ν), che è il rapporto tra deformazione laterale e longitudinale. Questo esperimento introdurrà le attrezzature tipiche utilizzate in un laboratorio di materiali da costruzione per misurare la forza (o lo stress) e la deformazione (o deformazione), e le utilizzerà per misurare E e ν di una tipica barra di alluminio.

Il modello più comune utilizzato per l'analisi è l'elasticità lineare (legge di Hooke), che postula che i cambiamenti di forza (F) sono direttamente proporzionali ai cambiamenti di dimensione (Δ). Nella sua forma più semplice nei casi di carico uniassiale, forza e deformazione sono correlate da una singola costante (E), o dal modulo di elasticità:

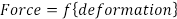(Eq. 1)

(Eq. 2)

(Eq. 3)

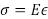(Eq. 4)

Come descritto nelle equazioni precedenti, lo stress e la deformazione sono quantità ingegneristiche, al contrario delle quantità vere. Le quantità vere richiedono di misurare i piccoli ma finiti cambiamenti nelle dimensioni locali che si verificano quando le forze aumentano. Sperimentalmente, questa impresa è molto difficile da realizzare, anche con i recenti progressi nelle tecnologie di misurazione senza contatto. Per questi calcoli, si può presumere che tali modifiche siano trascurabili e utilizzare l'area originale (A₀) e la lunghezza (L₀).

Per determinare il modulo di elasticità dalle equazioni di cui sopra, è necessario avere un modo per determinare i cambiamenti di forza e lunghezza quando viene caricato un campione. In un esperimento grezzo, si potrebbe usare una bilancia da bagno e un righello per svolgere questi compiti. In primo luogo, si potrebbe prendere un elastico spesso, misurarne le dimensioni e segnare due punti sulla banda separati da un pollice. Successivamente, si potrebbe posizionare un contenitore aperto su una bilancia e aggiungere acqua fino a quando la lettura è di dieci libbre. Si potrebbe quindi sospendere il contenitore con l'elastico e misurare quanto i due segni si sono separati. Questa misurazione ci fornirà tutti i dati necessari per calcolare E per la gomma poiché abbiamo tutti i valori necessari per risolvere E in Eqs. (da 2) a (4). Tuttavia, ci saranno incertezze ed errori molto grandi associati alla misurazione a causa del dispositivo di misurazione molto grezzo. Poiché l'entità della deformazione da misurare per i materiali da costruzione tipici è dell'ordine di 1x10^-6,sono necessari dispositivi di misurazione molto più accurati per determinare sperimentalmente le costanti del materiale. Per le applicazioni ingegneristiche più comuni, queste misurazioni si basano su estensimetri di resistenza elettrica. Poiché questi dispositivi verranno utilizzati nei video successivi, verrà fornita una descrizione dei loro principi di funzionamento.

Un estensime è un lungo filo ad anello incorporato su una matrice portante (Fig. 2). L'estensimetrico viene incollato al materiale da testare con una resina epossidica ad alta resistenza. Quando il materiale è deformato, i fili cambieranno di lunghezza e la loro resistenza cambierà leggermente di conseguenza. Quando il misuratore viene inserito come parte di un circuito a ponte di Wheatstone, questi cambiamenti possono essere rilevati come cambiamenti di tensione. L'avvento dei sistemi di misura digitali ha ridotto considerevolmente il rumore di fondo e altre fonti di errore all'interno del circuito, migliorando così la precisione con cui oggi è possibile misurare le variazioni di tensione. L'estensimetrio viene calibrato utilizzando una costante nota come fattore di misurazione, in modo che la sua uscita sia linearmente correlata alla deformazione per un determinato intervallo di deformazione sotto un dato ingresso di tensione.

Un estensimetri misura il ceppo in una sola direzione. Per ottenere lo stato completo di sollecitazione in un punto su una superficie, è necessario un estensimetri a rosetta, composto da tre estensimetri allineati a 45º l'uno all'altro (Fig. 3). Con queste misurazioni in tre direzioni diverse, l'intero stato di sollecitazione su una superficie può essere definito utilizzando principi come il cerchio di Mohr per calcolare le deformazioni e le sollecitazioni principali massime e minime.

Figura 2: Estensimetri.

Figura 3: Estensimetri a rosetta.

Le misurazioni della forza sono effettuate anche con estensimetri; tuttavia, queste misurazioni sono generalmente prese in una configurazione a ponte completo (cioè, le resistenze interne in un circuito a ponte di Wheatstone sono sostituite da misuratori attivi esterni) risultando in un dispositivo chiamato cella di carico. La cella di carico stessa è solitamente un cilindro in acciaio spesso e ad alta resistenza con due misuratori installati longitudinalmente e due installati trasversalmente per eliminare gli effetti del rapporto di Poisson. La calibrazione di una cella di carico richiede l'utilizzo di pesi morti in modo che l'uscita di tensione del circuito possa essere correlata a un determinato carico. Negli Stati Uniti, il National Institute of Science and Technology (NIST) calibra celle di carico fino a 5 milioni di kN utilizzando pesi morti e meccanismi a leva. Tutte le celle di carico utilizzate negli Stati Uniti devono essere riconducibili a questa fonte di calibrazione. In pratica, la tracciabilità significa che la cella di carico A viene calibrata dal NIST utilizzando pesi morti, portata in altri laboratori e installata in serie con la cella di carico B. Infine, la cella di carico B viene calibrata in base al confronto tra la sua uscita e l'uscita della cella di carico A. Tutte le celle di carico devono essere periodicamente calibrate per garantire che funzionino correttamente.

In genere, la cella di carico viene installata su una macchina di prova universale (UTM). Un UTM è costituito da un telaio autoreattante con due colonne a vite che vengono ruotate da un motore (Fig. 4). Bloccando un campione di prova nelle impugnature UTM e ruotando la colonna della vite in modo tale che la traversa si muova verso l'alto, le forze di trazione vengono introdotte nel campione. La forza applicata viene misurata dalla cella di carico, che viene installata in serie con il campione. D'altra parte, se le piastre sono installate al posto delle impugnature a trazione e le colonne delle viti vengono spostate verso il basso, le forze di compressione vengono introdotte nel campione di prova (cioè per testare i cilindri di cemento).

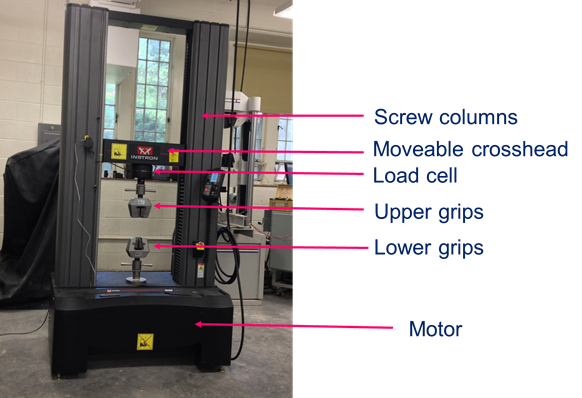
Figura 4: Macchina di prova universale.

Ora che è stato dimostrato come misurare la deformazione e la forza, verrà discusso un trattamento più generale della teoria dell'elasticità. Osservando un pezzo generico di una struttura sottoposta a carichi, si possono scrivere equazioni di equilibrio per forze e momenti lungo tutti gli assi.

Ciò si traduce in una serie di equazioni per ceppi normali (ε) e di taglio (γ) della forma:

(Eq. 5)

(Eq. 6)

Sei equazioni di questo tipo, tre per ceppi normali (ε_x, ε_y e ε_z) e tre per ceppi di taglio (γ_xy, γ_yz e γ_zx) sono necessarie per stabilire le deformazioni globali. Queste equazioni contengono tre costanti materiali: il modulo di elasticità (E), il rapporto di Poisson (ν) e il modulo di taglio (G). Come mostrato nell'equazione sopra, il modulo di taglio è il cambiamento della deformazione angolare data una sollecitazione di taglio o una trazione superficiale. Il rapporto di Poisson è definito come:

(Eq. 7)

Si può dimostrare che:

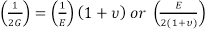= G (Eq. 8)

Pertanto, solo due delle tre costanti devono essere determinate per definire tutte e tre. Ci sono numerose altre costanti derivate che vengono utilizzate nella teoria dell'elasticità, che possono essere derivate da queste misurazioni. Ad esempio, il modulo di massa (B), o la variazione relativa del volume di un corpo prodotta da un'unità di compressione o tensione che agisce uniformemente sulla sua superficie, è:

Da Eqs. (5) e (6), si può determinare lo stato di sollecitazione e deformazione su una superficie se vengono effettuate almeno tre misurazioni indipendenti della deformazione. Se si utilizza un misuratore di deformazione a rosetta, che ha tre misuratori a 45° l'uno dall'altro (Fig. 3) al posto di un singolo misuratore longitudinale, allora si possono trovare i ceppi principali massimi e minimi (ε₁, ε₂) e l'angolo (Φ) tra i ceppi misurati e i ceppi principali del cerchio di Mohr.

Per un estensimetri a rosetta rettangolare, come quello mostrato in Fig. 3 in cui i misuratori sono a 45 gradi l'uno dall'altro:

(Eq. 9)

Φ =

L'intervallo di deformazioni su cui si mantengono le relazioni elastiche lineari è compreso tra zero e il limite proporzionale del materiale. In questo esperimento, che utilizzerà l'alluminio, la gamma di ceppi sarà mantenuta ben al di sotto di tale limite.

Useremo un semplice fascio a sbalzo strumentato con estensimetri per aiutare a illustrare i concetti di deformazione e sollecitazioni principali e il calcolo del modulo di Young (E) e del rapporto di Poisson (ν).  La trave a sbalzo verrà caricata in modo incrementale con una serie di pesi e le corrispondenti variazioni di deformazione registrate.  Le sollecitazioni corrispondenti possono essere calcolate dalla semplice equazione della sollecitazione di flessione:

(Eq. 11)

dove M è il momento (o forza moltiplicata per il suo braccio di leva), c è la distanza dal centroide alla fibra estrema nel raggio attraverso la sua profondità ( ), e I è il momento di inerzia, dato da dove b è la larghezza del fascio e t è il suo spessore.

Modulo di elasticità e rapporto di Poisson

Si presume che gli studenti siano stati addestrati all'uso e alle precauzioni di sicurezza necessarie per utilizzare una macchina di prova universale.

1. Ottenere una barra rettangolare in alluminio (12 pollici x 1 pollici x 1/4 pollici); si consiglia un alluminio 6061 T6xxx o più forte. Un foro deve essere praticato a circa 1 pollice da un'estremità del raggio per fungere da punto di carico.
2. Contrassegnare una posizione sulla trave a circa 8,0 pollici dal centro del foro sulla superficie superiore della trave. Disegnare segni di allineamento per gli estensimetri a rosetta e assicurarsi che gli assi della rosetta siano inclinati con un piccolo angolo (da circa 10° a 15°) rispetto all'asse longitudinale del fascio.
3. Contrassegnare una posizione simile sulla superficie inferiore del raggio. Qui verrà installato un singolo estensimetri e dovrebbe essere allineato con gli assi longitudinali della trave.
4. Misurare attentamente la larghezza (b) e lo spessore (t) della barra utilizzando le pinze. Eseguire tre repliche in tre posizioni diverse per ottenere una buona media delle dimensioni. Da queste misurazioni, calcolare il momento di inerzia (I) e la distanza dall'asse neutro alla fibra estrema della barra (c=t/2).
5. Ottenere un estensimetri a rosetta con una griglia di rilevamento di circa 1/4 di lunghezza per 1/8 mm di larghezza su ciascun misuratore e un estensimetrio singolo simile. Prendere nota dei fattori di calibrazione (o fattore di misurazione) per tutti i misuratori.
6. Per installare l'estensimetri a rosetta, prima sgrassare e pulire attentamente la superficie; levigare la superficie utilizzando carta vetrata progressivamente più fine fino ad ottenere una superficie molto liscia; pulire la superficie con un neutralizzatore; e incollare l'estensimetri secondo le specifiche del produttore. Lasciare che la colla si polimerizza correttamente prima di procedere.
7. Testare la resistenza dei misuratori (tipicamente 120 ohm) e la loro perdita di corrente alla barra (resistività, idealmente maggiore di 5 Mohm) prima di procedere.
8. Ripetere i passaggi da 1,5 a 1,7 per l'installazione del singolo misuratore sulla superficie inferiore.
9. Inserire il campione nell'apparecchio a sbalzo e fissare in modo appropriato.
10. Collegare gli estensimetri a un dispositivo di registrazione, ad esempio un indicatore di deformazione Vishay P3. Assicurarsi che il cablaggio sia corretto secondo le istruzioni dell'indicatore di deformazione e che si sappia quale canale corrisponde a ciascun estensime.
11. Immettere i fattori di misurazione appropriati per ciascun misuratore nell'indicatore.
12. Controllare la calibrazione del dispositivo inserendo una tensione nota che si tradurrà in una lettura di 5000με ad un fattore di misurazione di 2,00.
13. Registrare il carico iniziale e le tensioni.
14. Applicare lentamente 9 incrementi di 1,1 libbre (0,5 kg) o simili all'estremità del fascio. Metti in pausa ad ogni passo e consenti alle misurazioni di stabilizzarsi prima di registrare le letture.
15. Applicare lentamente 9 decrementi di 1,1 libbre (0,5 kg) o simili. Metti in pausa ad ogni passo e consenti alle misurazioni di stabilizzarsi prima di registrare le letture.
16. Scollegare l'estensimetri dall'indicatore di deformazione e spegnere l'indicatore.
17. Traccia la deformazione nel misuratore longitudinale rispetto alla deformazione nel misuratore trasversale. La pendenza di questa linea corrisponde al rapporto di Poisson, v.
18. Determinare la pendenza della linea di adattamento migliore dal grafico di sollecitazione rispetto alla deformazione longitudinale, che è uguale al modulo di Young, E.
19. Confronta i tuoi valori di E e v con valori precedentemente stabiliti o pubblicati (in generale, ci sarà un intervallo di valori dati piuttosto che un singolo valore discreto).

I dati devono essere importati o trascritti in un foglio di calcolo per una facile manipolazione e grafici. I dati raccolti sono riportati nella Tabella 1.

Poiché l'estensimetri a rosetta non è allineato con gli assi principali del fascio, i ceppi a rosetta devono essere inseriti nelle equazioni per ε_1,2 (Eq. 9) e ε (Eq. 10) di cui sopra per calcolare i ceppi principali, risultando nei dati mostrati nella Tabella 2. La tabella mostra che l'angolo tra la sollecitazione misurata e le sollecitazioni principali è di circa 0,239 radianti o 13,7°. Si noti che la deformazione principale massima è positiva, corrispondente a una grande tensione di trazione longitudinalmente; il ceppo principale minimo è negativo, corrispondente a un ceppo compressivo trasversale più piccolo. Il rapporto tra i ceppi principali minimi e massimi corrisponde al rapporto di Poisson, che è mostrato nell'ultima colonna e media circa 0,310.

	Carico	Gage 1	Gage 2	Gage 3	Gage 44
Passo	(Libbre.)	με	με	με	με
1	0.00	1	1	1	0
2	1.10	83	56	-21	-87
3	2.21	163	115	-41	-171
4	3.31	243	171	-62	-254
5	4.42	325	228	-83	-338
6	5.52	400	280	-104	-423
7	6.62	485	338	-122	-501
8	7.73	557	386	-143	-589
9	8.83	634	442	-163	-665
10	9.93	714	502	-184	-741
11	8.83	637	445	-162	-664
12	7.73	561	391	-142	-584
13	6.62	483	335	-123	-506
14	5.52	406	281	-102	-423
15	4.42	323	227	-83	-339
16	3.31	245	171	-62	-256
17	2.21	164	115	-41	-170
18	1.10	83	56	-21	-87
19	0.00	1	0	1	2

Tabella 1: Ceppi in barra di alluminio.

Fattore Gage	1	2	3	Sforzo principale massimo	Minimo. Ceppo principale	Angolo	Rapporto di Poisson
Fase di caricamento	με	με	με	(Eq. 9)	(Eq. 9)	(Eq. 10)	(Eq. 7)
1	1	1	1	1	1	0	0
2	83	56	-21	89	-26	-0.223	0.297
3	163	115	-41	176	-55	-0.243	0.311
4	243	171	-62	263	-82	-0.242	0.312
5	325	228	-83	351	-109	-0.240	0.311
6	400	280	-104	432	-136	-0.240	0.314
7	485	338	-122	523	-160	-0.237	0.307
8	557	386	-143	600	-186	-0.236	0.310
9	634	442	-163	684	-213	-0.238	0.312
10	714	502	-184	773	-242	-0.242	0.314
11	637	445	-162	688	-213	-0.239	0.309
12	561	391	-142	605	-186	-0.237	0.308
13	483	335	-123	520	-161	-0.236	0.309
14	406	281	-102	437	-133	-0.234	0.303
15	323	227	-83	349	-109	-0.241	0.313
16	245	171	-62	264	-81	-0.238	0.308
17	164	115	-41	177	-54	-0.239	0.302
18	83	56	-21	89	-26	-0.223	0.297
19	1	0	1	2	0	0.000	0.000
					Nella media	-0.239	0.310

Tabella 2: Principali deformazioni e angolo di inclinazione.

I ceppi principali massimi e minimi della Tabella 2 sono tracciati nella Fig. 5 che mostra tendenze molto lineari (R² = 0,999) per il rapporto di Poisson. Il valore ottenuto per il rapporto di Poisson (0,31), che corrisponde alla pendenza della linea, è molto vicino allo 0,30 indicato nella maggior parte dei riferimenti per l'alluminio e altri metalli.

Figura 5: Dati di deformazione principali che mostrano la pendenza della linea tra la deformazione principale massima e minima, che corrisponde al rapporto di Poisson.

Una buona interpretazione fisica dei dati dell'estensimetrio a rosetta può essere ottenuta tracciando i ceppi principali su un cerchio di Mohr (Fig. 6). Si noti che le tre misurazioni, mostrate qui per il caso del carico massimo di 7,4 libbre, corrispondono a tre punti del cerchio a 90º l'uno dall'altro, a partire da un angolo di circa 27,4º (o 2Φ) in senso antiorario dall'asse x.

Figura 6: Significato fisico delle letture delle rosette di ceppo mostrate sul cerchio di Mohr per ceppo.

La tabella 3 mostra i carichi, i risultati per la tensione di trazione principale dal singolo misuratore sul lato inferiore della trave (Gage 4, che è in compressione), il rapporto tra le sollecitazioni principali massime inferiori e superiori, la sollecitazione da Eq. (11) e il modulo di Young (E) come rapporto tra la sollecitazione da Eq. (11) divisa per la deformazione da Eq. (9). Nella Tabella 3, il modulo di Young è calcolato come 10147 ksi prendendo la media dei moduli calcolati per le 15 fasi intermedie di carico.

	Carico	Max. Preside. Sforzo	Stress principale massimo	Stress principale minimo	Sollecitazione di flessione	Modulo di Young
Fase di caricamento	Lbs.	με	Ksi	Ksi	Psi	Ksi
1	0.00	1	10	9	0	0
2	1.10	89	886	0	882	9945
3	2.21	176	1765	0	1763	9991
4	3.31	263	2630	0	2645	10058
5	4.42	351	3513	0	3526	10038
6	5.52	432	4324	0	4408	10195
7	6.62	523	5230	0	5290	10113
8	7.73	600	6001	0	6171	10283
9	8.83	684	6843	0	7053	10307
10	9.93	773	7726	0	7935	10269
11	8.83	688	6877	0	7053	10256
12	7.73	605	6051	0	6171	10198
13	6.62	520	5204	0	5290	10165
14	5.52	437	4368	0	4408	10091
15	4.42	349	3494	0	3526	10092
16	3.31	264	2644	0	2645	10004
17	2.21	177	1770	0	1763	9960
18	1.10	89	886	0	882	9945
19	0.00	2	19	0	0	0
					Nella media	10147

Tabella 3: Calcolo del modulo di elasticità (E).

I dati per E sono tracciati anche in Fig. 7, che indica un'eccellente relazione lineare (alto R²⁾tra stress e deformazione e una pendenza di circa 10.147 ksi. La differenza tra il modulo della Tabella 3 e quello della Fig. 6 sorge perché i calcoli per la pendenza in Fig. 6 richiedono che l'intercetta vada attraverso lo zero. Le magnitudini si confrontano molto favorevolmente (errore inferiore all'1,5%) con i valori pubblicati di E per l'alluminio 6061T6, che di solito è dato come 10.000 ksi.

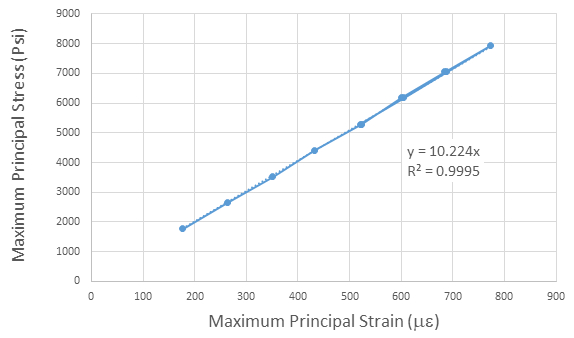
Figura 7: La pendenza della linea di massima sollecitazione rispetto alla massima deformazione è il modulo di Young.

Infine, riformulando Eqs. 5) e 6) in:

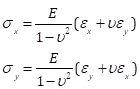(Eq. 12)

possiamo calcolare le sollecitazioni principali usando il cerchio di Mohr. Nel caso del passo corrispondente a 6,61 libbre di carico, le principali deformazioni di (634, -189) portano a sollecitazioni principali di (7,34, 0,00) ksi (Fig. 8). Sebbene i calcoli qui siano fatti usando le espressioni per la sollecitazione piana, i risultati indicano correttamente che lungo l'asse principale la sollecitazione nella direzione perpendicolare è zero (o molto vicina ad essa), corrispondente al caso del carico uniassiale. I valori di sollecitazione con un angolo di 2Φ = 0,40 radianti sono (6,50, 2,82) ksi.

Figura 8: Cerchio di Mohr per la sollecitazione piana per il caso di un carico di 7,34 libbre.

In questo esperimento sono state misurate due costanti materiali fondamentali: il modulo di elasticità (E) e il rapporto di Poisson (v). Questo esperimento dimostra come misurare queste costanti in un ambiente di laboratorio usando un estensimetri a rosetta. I valori ottenuti sperimentalmente corrispondono bene ai valori pubblicati di 10.000 ksi e 0,3, rispettivamente. Questi valori sono fondamentali nell'applicazione della teoria dell'elasticità per la progettazione ingegneristica, e questa tecnica sperimentale qui descritta è tipica di quelle utilizzate per ottenere costanti di materiali. Per ottenere questi valori, è necessario prestare molta attenzione sia nell'utilizzo di strumentazione ad alta risoluzione che in procedure di calibrazione tracciabili. In particolare, l'uso di dispositivi basati su estensimetri e sistemi di acquisizione dati digitali da 16 a 24 bit sono parte integrante del successo e della qualità di tali esperimenti.

Oggi, ci sono altri metodi per determinare il modulo di Young di un materiale, compresi i metodi di propagazione delle onde (metodo dell'eco-impulso ultrasonico) e la nanoindentazione. Uno dei vantaggi dell'utilizzo della propagazione delle onde è che è uno dei metodi non distruttivi per misurare il modulo di Young, mentre la nanoindentazione e l'uso di un estensimetrico a rosetta sono metodi più invasivi.

La progettazione di qualsiasi prodotto ingegneristico, da un tostapane a un grattacielo, richiede l'utilizzo di modelli analitici efficaci per migliorare e ottimizzare il design. La teoria dell'elasticità è alla base della maggior parte dei modelli utilizzati nella progettazione di ingegneria civile e si basa sulla creazione di diverse costanti.

I modelli analitici sono necessari quando verranno costruite solo una singola (o pochissime) repliche. Poiché il costo e le prestazioni della struttura dipendono dal risultato di tali analisi e tali analisi, a loro volta, dipendono dall'avere valori solidi per le proprietà del materiale, devono essere eseguiti test come quelli qui descritti per garantire il controllo di qualità e la garanzia della qualità nel processo di costruzione. Per esempio:

• Nella scelta di una facciata per un edificio, l'architetto deve fare attenzione a progettare un involucro impermeabile. La tenuta all'acqua di una facciata di un edificio in mattoni può dipendere dal mantenimento della malta tra i mattoni non rasata, tra gli altri fattori. Se la malta si incrina, l'acqua penetrerà e causerà problemi di corrosione e umidità che saranno molto costosi da risolvere. Per determinare quanta forza la malta può resistere prima che si rompa, abbiamo bisogno sia di una teoria che delle costanti associate. L'architetto e l'ingegnere strutturale devono lavorare insieme per determinare quali carichi vedrà la facciata (auto-peso, vento, pioggia battente, ecc.) e come ogni opzione di progettazione si comporterà in tali condizioni. Solo allora può essere scelta una malta con le caratteristiche appropriate.
• Nella costruzione di un edificio alto, come il Burj Dubai, la società di costruzioni deve prestare molta attenzione a mantenere i pavimenti a livello. Man mano che la costruzione procede, se le dimensioni delle colonne e delle pareti sono diverse, alcuni di questi elementi possono accorciarsi (sforzarsi) più di altri man mano che la costruzione progredisce e viene aggiunto più peso (stress). Per ottenere pavimenti piani alla fine della costruzione, la società di costruzioni dovrà apportare modifiche all'altezza delle colonne e delle pareti nei piani inferiori - i piani inferiori potrebbero non essere livellati durante le fasi iniziali della costruzione, ma dovrebbero essere piatti alla fine. Per calcolare come effettuare correttamente queste regolazioni, la società di costruzioni assumerà un ingegnere strutturale per fornire dati sulle altezze differenziali delle colonne e delle pareti. L'ingegnere dovrà utilizzare costanti di materiale per eseguire questi calcoli.
• Nella progettazione di una lattina di soda, un produttore deve ridurre al minimo lo spessore della parete di alluminio, poiché l'alluminio è un materiale molto costoso. Per ottimizzare la forma e le dimensioni delle lattine, il produttore deve determinare quali condizioni di carico sono importanti; le condizioni di trasporto e stoccaggio possono essere più impegnative di quelle che il consumatore beve da esso. Molte di queste condizioni saranno difficili e costose da replicare all'interno di un programma di test sperimentali; il produttore può scegliere di fare molte analisi per ottimizzare le dimensioni della lattina prima di passare alla fase di prototipo. Questa procedura è ciò che Boeing ha seguito nello sviluppo del Dreamliner (Boeing 787). Per fare questi studi, le proprietà del materiale devono essere conosciute e la teoria appropriata selezionata.