הדמיה של זרימה בעבר גוף בלוף

Overview

מקור: ריקרדו מג'יה-אלווארז, חוסאם היקמט ג'באר ומחמוד נ. עבדולטיף, המחלקה להנדסת מכונות, אוניברסיטת מישיגן סטייט, מזרח לנסינג, MI

בשל האופי הלא ליניארי של החוקים השולטים בו, תנועה זורמת תורמת לדפוסי זרימה מסובכים. הבנת טבעם של דפוסים אלה הייתה נושא לבחינה קפדנית במשך מאות שנים. למרות שמחשבים אישיים ומחשבי-על משמשים רבות להסיק דפוסי זרימת נוזלים, היכולות שלהם עדיין אינן מספיקות כדי לקבוע את התנהגות הזרימה המדויקת לגיאומטריות מורכבות או זרימות אינרציאליות מאוד (למשל כאשר המומנטום שולט על התנגדות צמיגה). לאור זאת, פותחו שפע של טכניקות ניסיוניות להגייה של דפוסי זרימה שיכולים להגיע למשטרי זרימה וגיאומטריות שאינם נגישים לכלים תיאורטיים וחישוביים.

הדגמה זו תחקור זרימת נוזלים סביב גוף בלוף. גוף בלוף הוא אובייקט שבשל צורתו גורם לזרימה מופרדת על פני רוב פני השטח שלו. זאת בניגוד לגוף יעיל, כמו חיל אוויר, אשר מיושר בנחל וגורם פחות הפרדת זרימה. מטרת המחקר היא להשתמש בבועות מימן כשיטה להדמיית דפוסי זרימה. בועות המימן מיוצרות באמצעות אלקטרוליזה באמצעות מקור כוח DC על ידי טביעת האלקטרודות שלה במים. בועות מימן נוצרות באלקטרודה השלילית, אשר צריך להיות חוט עדין מאוד כדי להבטיח כי הבועות להישאר קטן ולעקוב אחר תנועת נוזלים בצורה יעילה יותר. שיטה זו מתאימה לזרימות למינאר יציבות ולא יציבות, ומבוססת על קווי הזרימה הבסיסיים המתארים את אופי הזרימה סביב עצמים. [1-3]

מאמר זה מתמקד בתיאור יישום הטכניקה, לרבות פרטים על הציוד והתקנתו. לאחר מכן, הטכניקה משמשת כדי להדגים את השימוש בשני קווי זרימה בסיסיים כדי לאפיין את הזרימה סביב גליל עגול. קווי זרימה אלה משמשים להערכת כמה פרמטרי זרימה חשובים כמו מהירות זרימה ומספר ריינולדס, ולקבוע דפוסי זרימה.

Principles

בתצורה זו, נשקול זרימה אחידה ויציבה של מים במהירות (המכונה מהירות זרם חופשי) המתקרבת לצילינדר מעגלי (איור 1). בהתאם לתנאי הזרימה כפי שהם מאופיינים במספר ריינולדס, זרימה זו עלולה להפוך לבלתי יציבה ולהוליד שפיכת מערבולת. שפיכת מערבולת אופיינית בזרימה מעבר לגופי בלוף, אשר בניגוד לגופים יעילים, מפגינים הפרדת שכבות גבול על חלק ניכר מפני השטח שלהם. הפרדת שכבת גבול זו מובילה להיווצרות מערבולות מאחורי הגוף שעלולות בסופו של דבר להתנתק מעת לעת לתוך האשכבה. כאשר מתרחשת ניתוק תקופתי, מערבולות ליצור אזורים לסירוגין של לחץ נמוך מאחורי הגוף שיכול להפוך עומסים מהדהדים אם תדירות שפיכה עולה בקנה אחד עם התדירות הטבעית של הגוף. תהליך שפיכת המערבולת נקרא "רחוב מערבולת פון קרמן" (איור 2). דפוס חוזר זה של מערבולות מסתחררות נגרמת על ידי הפרדת זרימה לא יציבה סביב גוף הבלוף ומתרחשת בטווחים מסוימים של מספר ריינולדס. הימנעות מתרחיש זה היא בעלת חשיבות משמעותית בתכנון מבנים הנדסיים כגון ערימות עשן ועמודי גשר מכיוון שהוא עלול לגרום לכשל קטסטרופלי.

איור 1. תעברו על פני גליל עגול. סכמטי של תצורה בסיסית. זרם הומוגני עם מהירות מתקרב לצילינדר ישר בקוטר שציר הסימטריה שלו מאונך למהירות המתקרבת.

מספר ריינולדס הוא פרמטר חסר ממד המוגדר כיחס בין כוחות אינרציאליים לכוחות צמיגים:

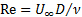(1)

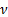איפה הצמיגות הקינמטית של הנוזל, מהירות אופיינית (במקרה הנוכחי) 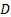וקוטר הגליל. מספר ריינולדס הוא ללא ספק הפרמטר החשוב ביותר באפיון זרימת הנוזלים וישמש לאורך הניסוי הנוכחי כמדד להופעת רחוב מערבולת פון קרם. בפרט, כאשר מספר ריינולדס הוא סביב 5, הזרימה מציגה שני מערבולות סיבוב נגד יציב מאחורי הגליל. ככל שמספר ריינולדס גדל, שני מערבולות אלה להאריך את כיוון הזרימה. כאשר מספר ריינולדס מגיע לערך של כ -37, האשכבה הופכת לבלתי יציבה ומתחילה להתנדנד בסינוסואידית כתוצאה מחוסר איזון בין לחץ למומנטום. עלייה נוספת במספר ריינולדס עד 47 גורמת לשתי מערבולות מסתובבות להתנתק מהגליל ברצף לסירוגין העוקב אחר תנודות ההתעוררות הסינוסואידליות [4,5,6].

התדירות שבה מערבולות נ לשפך את הגליל אינו קבוע; זה משתנה עם הערך של מספר ריינולדס. תדירות שפיכת מאופיין על ידי מספר Strouhal, המהווה את הפרמטר האחר ללא ממד של רלוונטיות בתצורת זרימת נוזל מסוים זו:

(2)

כאן, הוא תדר שפיכת המערבולת ואת סולמות האורך והמהירות זהים למספר ריינולדס. לאחר מכן ניתן לאפיין את תדר שפיכת המערבולת במספר סטרוהאל כפונקציה ליניארית של השורש הריבועי ההופכי של מספר ריינולדס [7]:

(3)

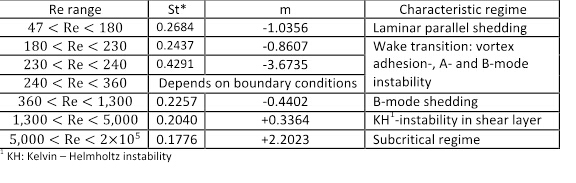
פונקציה זו אינה תמיד מונוטונית, היא מציגה מעברים נוספים כתוצאה מאי-יציבות משנית המגיעה לאי-ליניאריות של זרימת הנוזלים. כתוצאה מכך, מקדמים 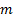ישתנו בהתאם לטווח המספרים של ריינולדס. טבלה 1 מציגה את הערכים של מקדמים אלה למשטרי הזרימה שאופיינו היטב בספרות [7].

במהלך הניסויים הנוכחיים, נשתמש בקווי זרימה כדי לחקור זרימה חיצונית סביב גליל עגול. קווי זרימה אלה מוגדרים באופן הבא:

• Pathline: נתיב כי חלקיק נוזל עוקב כפי שהוא נע עם הזרימה.

• סטרקלין: לוקוס רציף של כל חלקיקי הנוזלים שתנועתם מקורה באותו מיקום מרחבי.

• ציר זמן: קבוצה של חלקיקי נוזלים שתויגו באותו רגע של זמן תוך יצירת לוקוס רציף.

• ייעול: קו רציף שנמצא בכל מקום משיק לשדה המהירות ברגע בזמן.

שלושת הקווים הראשונים קלים יחסית ליצירה ניסיונית, בעוד שייעולים הם רק מושג מתמטי שבאופן כללי צריך להיות מיוצר על ידי לאחר עיבוד לכידה מיידית של שדה המהירות. למרות שזה תמיד נכון, הניתוח מפשט באופן משמעותי בזרימות קבועות מכיוון שקווי נתיב, פסים וייעול חופפים זה לזה. לעומת זאת, קווים אלה בדרך כלל אינם חופפים זה לזה בזרימות לא יציבות. יישום טכניקה זו הוא בדרך כלל פשוט ודורש ציוד בעלות נמוכה בלבד, בניגוד לטכניקות מתוחכמות ויקרות יותר כגון ולוצימיטריה של תמונת חלקיקים [1], ולוצימיטריה למעקב אחר חלקיקים [8,9] ו-Velocimetry תיוג מולקולרי [10].

איור 2. תוצאות מייצגות. (A) גיליון רציף של בועות מימן המציג פסים כתוצאה מהפרעות במעלה הזרם. הצל שמטיל המוט משמש לקביעת ההמרה ממכונה ליחידות אמיתיות. מחזור שפיכת מערבולת מאויר גם כדי לעזור לקבוע את תדירות שפיכת כראוי. (B) צירי זמן שנוצרו עם בועות מימן. מכיוון שתדר ציר הזמן מוגדר היטב, ניתן להשתמש בהם כדי למדוד את מהירות הזרימה במדויק; ספירת צירי הזמן המוקפים בקווים האדומים תשמש להערכה זו. אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.

טבלה 1. ערכים של מקדמים עבור מרווחי זמן שונים של ריינולדס (מתוך [8]).

Procedure

1. כדי לייצר גיליון רציף של בועות:

הגדר את הציוד בהתאם לדיאגרמה החשמלית המוצגת באיור 3.
תקן את האלקטרודה החיובית במים בקצה הזרם של מקטע הבדיקה (ראו איור 4 לעיון).
תקן את האלקטרודה השלילית במעלה הזרם ובסמוך לנקודת העניין כדי לשחרר את הבועות לזרם לפני שהזרימה מגיעה למושא המחקר (ראו איור 4 לעיון). המים משלימים את המעגל בין שתי האלקטרודות.
הפעלת מתקן הזרימה
הגדר את לוח המחוגות של בקר התדר למיקום 2. זה יקבע קצב זרימה של כ 9x10^-4 מ^'3/s.
הפעל את ספק הכוח DC ולהגדיל את המתח עד כ 25 V, הזרם יהיה להגדיר את עצמו סביב 190 mA.
הגדר את צורת הגל במחולל האותות לגל מרובע (סימן: 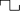). זה יוצר אות ריבועי V - 5 V שמפעיל את ממסר מצב מוצק (סגירת המעגל) במקומו הגבוה ופותח אותו במצב נמוך
במקרה הספציפי הזה, תדירות הגל המרובע אינה חשובה. זה פשוט צריך להיות לא אפס.
מקסם את היסט DC (+5 V) במחולל האותות. עם הגדרה זו, המעגל תמיד סגור והמערכת מייצרת בועות ברציפות.

איור 3. דיאגרמת חיבורים.

איור 4. מחלקת בדיקה. הזרימה עוברת משמאל לימין. האלקטרודה השלילית יוצרת שכבה של בועות מימן שנסחפות עם הזרימה. האלקטרודה החיובית מוגדרת בקצה במורד הזרם של קטע הבדיקה כדי למנוע את ההפרעות שלה. אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.

2. כדי לייצר צירי זמן:

הפעלת מתקן הזרימה
הגדר את לוח המחוגות של בקר התדר למיקום 2. זה יקבע קצב זרימה של כ 9x10^-4 מ^'3/s.
הפעל את ספק הכוח DC ולהגדיל את המתח עד כ 25 V, הזרם יהיה להגדיר את עצמו סביב 190 mA.
הגדר את צורת הגל במחולל האותות לגל מרובע (סימן: ). פעולה זו יוצרת אות ריבועי V - 5 V 0 המפעיל את ממסר מצב מוצק (סגירת המעגל) במקומו הגבוה ומנטרל אותו (פתיחת המעגל) במצב נמוך
הגדר את היסט DC במחולל האותות ב+ 1 V.
הגדר את התדר של הגל המרובע במחולל האותות ב-10 הרץ.
הגדר את הסימטריה של הגל המרובע שלילי מעט (-2) כדי להגדיל את הרווח בין צירי זמן תוך שמירה על התדר הנכון.

3. להשתמש בקווי זרימה כדי ללמוד את רחובות מערבולת פון קרמן:

למדוד את הקוטר של המוט, 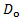באמצעות caliper. השתמש ביחידות S.I. למדידה זו (מ').
תקן מוט גלילי במורד הזרם של האלקטרודה השלילית.
השליכו את האור של מנורת הפריקה בעוצמה גבוהה על שכבת בועות המימן. ודא שהאור אינו נמצא ישירות מאחורי קו הראייה כדי למנוע רוויית יתר של מערכת ההדמיה
ישר את מערכת ההדמיה עם המוט; באופן שרק הקצה המעגלי נראה מול המצלמה.
הוסף סימן בחלון הפריט החזותי ובמורד הזרם של המוט כדי להשתמש בו כהפניה לספירת מחזורי סככה מערבולת לכל זמן יחידה.

4. ניתוח נתונים עבור זרימה מעבר לצילינדר מעגלי:

קביעת גורם ההמרה מיחידות מכונה ליחידות חלל אמיתיות:
1. מדוד את רוחב הצל שהטיל המוט בגליון הבועות (ראה איור 2(A) לעיון). קח מדידה זו ממש על המוט כדי למנוע עיוות עם מרחק. זהו הקוטר של המוט ביחידות מכונה, 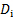(נקודות או פיקסלים, בהתאם לתבנית)
2. השתמש במשוואה הבאה כדי לקבוע את מקדם ההמרה מיחידות מחשב ליחידות בעולם האמיתי:
קביעת מהירות הזרימה:
1. בחר קבוצה של צירי זמן לא ממושמעים במעלה הזרם של גוף הבלוף.
2. מדוד את המרחק בין ציר הזמן הראשון והאחרון ביחידות מחשב (נקודות או פיקסלים).
3. ספר את מספר צירי הזמן בקבוצה , .
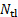4. שים לב לתדירות של אות הגל המרובע כפי המיוצר על ידי מחולל האות, .
5. קבעו את מהירות הזרימה המתקרבת מהמשוואה הבאה:
קביעת מספר ריינולדס:
1. מצא את הצמיגות הקינטמטית של נוזל העבודה (למשל מים m²/s).
2. חשב את מספר ריינולדס באמצעות משוואה (1). בשביל זה, בהתחשב בקוטר המוט ( 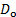) הנמדד בשלב 3.1, המהירות המתקרבת ( ) נקבעת עם משוואה (5), ואת הצמיגות הקינטמטית שנקבעה בשלב 4.3.1
קביעת מספר סטרוחאל: מערבולות בעקבות המוט נעות במהירות שונה כמו צירי הזמן בזרם החופשי. לפיכך, יש להעריך את תדירות שפיכת המערבולת באופן עצמאי.
1. הגדר הפניה קבועה במורד הזרם של המוט. הפניה זו יכולה להיות מחרוזת עדינה המחוברת לחלק החיצוני של המנהרה או קו דיגיטלי שנוסף לסרטון וידאו של תהליך הזרימה.
2. ספר את מספר מחזורי שפיכת 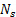המערבולת, חוצה את ההפניה במהלך פרק זמן מוגדר . מחזור שפיכת מערבולות מאויר באיור 2(א').
3. חשב את תדירות ההשלכה מהמשוואה הבאה:
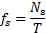
4. השתמש בתוצאות משוואות (5) ו- (6) במשוואה (2) כדי לחשב את מספר סטרוהול.

Results

איור 2 מציג שתי תוצאות מייצגות של הדמיית בועת מימן של רחוב מערבולת פון קרמן. איור 2(A) מציג דוגמה לשדה של פסים כפי שמעידות הפרעות בגליון בועת המימן. תמונה זו משמשת לחילוץ קוטר המוט ביחידות מכונה. איור 2(B) מציג דוגמה לשדה של צירי זמן. תמונה זו משמשת להערכת מהירות הנוזל המתקרבת. הפרמטרים שחולצו מניסוי מסוים זה מסוכמים בטבלה 2.

טבלה 2. תוצאות מייצגות לזרימה מעבר לצילינדר מעגלי.

פרמטר	ערך
D_o	0.003 מטר
D_i	14.528 נק'
f_s	2.169 הרץ
f_tl	10 הרץ
L	130.167 "pts"
M	4842.67 "pts" ∕"m"
N_s	60
N_tl	7
T	27.66 s
U_∞	0.0384 מטר/ש
ν	1.004×[10]^(-6) מ'²/s
מחדש	115
סנט	0.169

מכיוון שמספר ריינולדס הוא 115 עבור הדוגמה הנוכחית, ניתן לבדוק את תוקפה של תוצאה זו באמצעות משוואה (3) עבור

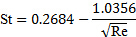(7)

שממנו אנו מקבלים:

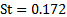(8)

לאחר השוואת הערכה זו לתוצאה הניסיונית שלנו (ראה טבלה 2 לעיון), אנו יכולים להסיק כי הניסוי שלנו הציע תוצאה משביעת רצון. איור 5 מציג קבוצה של תוצאות ניסוי בהשוואה לתחזיות המשוואה (7).

איור 5. תוצאות ניסוי. השוואה בין תוצאות הניסוי הנוכחיות לעומת תחזיות של הקשר בין מספר ריינולדס למספר סטרוהאל לזרימה מעבר לצילינדר מעגלי.

Application and Summary

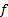במחקר זה, השימוש בבועות מימן הוכח כדי לחלץ מידע איכותי וכמותי מתמונות של זרימה סביב גליל עגול. המידע הכמותי שחולץ מניסויים אלה כלל את מהירות הזרם החופשי ( ), תדר שפיכת מערבולות ( ), מספר ריינולדס (Re) ומספר סטרוהאל (St). בפרט, התוצאות עבור St vs Re הציגו הסכמה טובה מאוד עם מחקרים קודמים [3].

בשל המהירות האיטית המשמשת בניסויים הנוכחיים, ההסתבפויות בגיליון הבועה מייצרות שכבת בועה מפוספסת. פסים אלה הם בעצם פסים. כאשר יריעת בועת המימן נעה במורד הזרם, פסים אלה מתעבים והופכים לא סדירים יותר. זוהי תוצאה של עוצמת מערבולת בזרם החופשי. ההשפעה מופחתת ככל שהמהירות של המנהרה גדלה מכיוון שהבועות עוזבות את קטע הבדיקה לפני שהן מציגות פיזור משמעותי. סטריקלינים יכולים גם להיות מיוצרים במקומות שנבחרו מראש על ידי ציפוי החוט תוך השארת חלקים קטנים ממנו חשופים למים.

התנהגות הזרימה הנוכחית חלה ישירות על זרימה של מבנים הנדסיים בעבר כגון עמודי גשרים ואסדות נפט מהחוף, מגדלי טורבינות רוח או עמודי חשמל אם להזכיר כמה. ולמעשה, התנהגות זו מוצגת על ידי גופים בלוף עם גיאומטריות אחרות מאשר גלילי כגון מגרדי שמיים. בהתחשב בכך מערבולות ליצור אינטראקציות מבנה נוזלים שהופכים מבנים תנודה, לדעת את תדרי שפיכת המערבולת שבה מבנה נתון ייחשף הוא קריטי לעיצוב שלה. בהקשר זה, המהנדס צריך לוודא כי התדירות הטבעית של המבנה אינה כזו שהיא מהדהדה בתדר שפיכת המערבולת, מכיוון שאפקט זה יוביל בהכרח לכישלון קטסטרופלי של המבנה. באמצעות חוקי קנה מידה מתאימים [10] ובועות מימן במנהרת מים, מהנדס יכול לדמות את האינטראקציה של זרימה עם מבנה לפני בנייתו כדי לוודא שעיצובו בטוח או כדי לברר אם הוא זקוק לשינויים כלשהם.

מלבד גופי בלוף, הדמיה של בועת מימן היא כלי רב עוצמה לחקר זרימה סביב גופים יעילים כגון חילות אוויר או גוף הספינה. על ידי שימוש בקווי זרימה שנוצרו בטכניקה זו, ניתן לקבוע פרמטרים כגון זווית ההתקפה שבה מתרחש דוכן, או אפילו להעריך מאפייני הרמה בהתבסס על מהירות הזרימה. חשוב מכך, דפוס העיוות של קווי נוזלים יעזור למהנדס לייעל את העיצוב שלו.

הדמיה עם בועות מימן אינה מוגבלת לזרימות חיצוניות כמו שהוזכר לעיל. שיטה זו יכולה לשמש גם כדי לבחון את הזרימה דרך ערוצים פתוחים או מערכות זרימה מוגבלות לחלוטין. במקרה האחרון, הקירות יצטרכו להיות שקופים כדי להבטיח גישה אופטית. לדוגמה, אם אחד מעוניין לעצב מפזר זרימה עבור זרימה תת קולית, בועות מימן יכול לשמש כדי לקבוע תנאי גיאומטריה וזרימה שעבורם מפזר יציג הפרדת זרימה וחוסר יציבות. בהתבסס על תצפיות אלה, העיצוב יכול להיות ממוטב באופן ניסיוני כדי להבטיח את הפונקציונליות הנכונה שלה.

References

Zöllner, F. Leonardo da Vinci 1452-1519: sketches and drawings, Taschen, 2004.
White, F. M. Fluid Mechanics, 7^th ed., McGraw-Hill, 2009.
Adrian, Ronald J., and Jerry Westerweel. Particle Image Velocimetry. Cambridge University Press, 2011.
Gerrard, J. H., The wakes of cylindrical bluff bodies at low Reynolds number, Phil. Trans. Roy. Soc. (London) Ser. A, Vol. 288, No. 1354, pp. 351-382 (1978)
Coutanceau, M. and Bouard, R., Experimental determination of the viscous flow in the wake of a circular cylinder in uniform translation. Part 1. Steady flow, J. Fluid Mech., Vol. 79, Part 2, pp. 231-256 (1977)
Kovásznay, L. S. G., Hot-wire investigation of the wake behind cylinders at low Reynolds numbers, Proc. Roy. Soc. (London) Ser. A, Vol. 198, pp. 174-190 (1949)
Fey, U., M. König, and H. Eckelmann. A new Strouhal-Reynolds-number relationship for the circular cylinder in the range . Physics of Fluids, 10(7):1547, 1998.
Maas, H.-G., A. Grün, and D. Papantoniou. Particle Tracking in three dimensional turbulent flows - Part I: Photogrammetric determination of particle coordinates. Experiments in Fluids Vol. 15, pp. 133-146, 1993.
Malik, N., T. Dracos, and D. Papantoniou Particle Tracking in three dimensional turbulent flows - Part II: Particle tracking. Experiments in Fluids Vol. 15, pp. 279-294, 1993.
Tropea, C., A.L. Yarin, and J.F. Foss. Springer Handbook of Experimental Fluid Mechanics. Vol. 1. Springer Science & Business Media, 2007.
Monaghan, J. J., and J. B. Kajtar. Leonardo da Vinci's turbulent tank in two dimensions. European Journal of Mechanics-B/Fluids. 44:1-9, 2014.
Becker, H.A. Dimensionless parameters: theory and methodology. Wiley, 1976.

Tags

Flow Visualization Bluff Body Flow Patterns Vortex Shedding Separation Circular Cylinder Boundary Layer Wake Vortices Low Pressure Von Karman Vortex Street Reynolds Number

1. כדי לייצר גיליון רציף של בועות:

הגדר את הציוד בהתאם לדיאגרמה החשמלית המוצגת באיור 3.
תקן את האלקטרודה החיובית במים בקצה הזרם של מקטע הבדיקה (ראו איור 4 לעיון).
תקן את האלקטרודה השלילית במעלה הזרם ובסמוך לנקודת העניין כדי לשחרר את הבועות לזרם לפני שהזרימה מגיעה למושא המחקר (ראו איור 4 לעיון). המים משלימים את המעגל בין שתי האלקטרודות.
הפעלת מתקן הזרימה
הגדר את לוח המחוגות של בקר התדר למיקום 2. זה יקבע קצב זרימה של כ 9x10^-4 מ^'3/s.
הפעל את ספק הכוח DC ולהגדיל את המתח עד כ 25 V, הזרם יהיה להגדיר את עצמו סביב 190 mA.
הגדר את צורת הגל במחולל האותות לגל מרובע (סימן: ). זה יוצר אות ריבועי V - 5 V שמפעיל את ממסר מצב מוצק (סגירת המעגל) במקומו הגבוה ופותח אותו במצב נמוך
במקרה הספציפי הזה, תדירות הגל המרובע אינה חשובה. זה פשוט צריך להיות לא אפס.
מקסם את היסט DC (+5 V) במחולל האותות. עם הגדרה זו, המעגל תמיד סגור והמערכת מייצרת בועות ברציפות.

איור 3. דיאגרמת חיבורים.

איור 4. מחלקת בדיקה. הזרימה עוברת משמאל לימין. האלקטרודה השלילית יוצרת שכבה של בועות מימן שנסחפות עם הזרימה. האלקטרודה החיובית מוגדרת בקצה במורד הזרם של קטע הבדיקה כדי למנוע את ההפרעות שלה. אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.

2. כדי לייצר צירי זמן:

הפעלת מתקן הזרימה
הגדר את לוח המחוגות של בקר התדר למיקום 2. זה יקבע קצב זרימה של כ 9x10^-4 מ^'3/s.
הפעל את ספק הכוח DC ולהגדיל את המתח עד כ 25 V, הזרם יהיה להגדיר את עצמו סביב 190 mA.
הגדר את צורת הגל במחולל האותות לגל מרובע (סימן: ). פעולה זו יוצרת אות ריבועי V - 5 V 0 המפעיל את ממסר מצב מוצק (סגירת המעגל) במקומו הגבוה ומנטרל אותו (פתיחת המעגל) במצב נמוך
הגדר את היסט DC במחולל האותות ב+ 1 V.
הגדר את התדר של הגל המרובע במחולל האותות ב-10 הרץ.
הגדר את הסימטריה של הגל המרובע שלילי מעט (-2) כדי להגדיל את הרווח בין צירי זמן תוך שמירה על התדר הנכון.

3. להשתמש בקווי זרימה כדי ללמוד את רחובות מערבולת פון קרמן:

למדוד את הקוטר של המוט, באמצעות caliper. השתמש ביחידות S.I. למדידה זו (מ').
תקן מוט גלילי במורד הזרם של האלקטרודה השלילית.
השליכו את האור של מנורת הפריקה בעוצמה גבוהה על שכבת בועות המימן. ודא שהאור אינו נמצא ישירות מאחורי קו הראייה כדי למנוע רוויית יתר של מערכת ההדמיה
ישר את מערכת ההדמיה עם המוט; באופן שרק הקצה המעגלי נראה מול המצלמה.
הוסף סימן בחלון הפריט החזותי ובמורד הזרם של המוט כדי להשתמש בו כהפניה לספירת מחזורי סככה מערבולת לכל זמן יחידה.

4. ניתוח נתונים עבור זרימה מעבר לצילינדר מעגלי:

קביעת גורם ההמרה מיחידות מכונה ליחידות חלל אמיתיות:
1. מדוד את רוחב הצל שהטיל המוט בגליון הבועות (ראה איור 2(A) לעיון). קח מדידה זו ממש על המוט כדי למנוע עיוות עם מרחק. זהו הקוטר של המוט ביחידות מכונה, (נקודות או פיקסלים, בהתאם לתבנית)
2. השתמש במשוואה הבאה כדי לקבוע את מקדם ההמרה מיחידות מחשב ליחידות בעולם האמיתי:
קביעת מהירות הזרימה:
1. בחר קבוצה של צירי זמן לא ממושמעים במעלה הזרם של גוף הבלוף.
2. מדוד את המרחק בין ציר הזמן הראשון והאחרון ביחידות מחשב (נקודות או פיקסלים).
3. ספר את מספר צירי הזמן בקבוצה , .
4. שים לב לתדירות של אות הגל המרובע כפי המיוצר על ידי מחולל האות, .
5. קבעו את מהירות הזרימה המתקרבת מהמשוואה הבאה:
קביעת מספר ריינולדס:
1. מצא את הצמיגות הקינטמטית של נוזל העבודה (למשל מים m²/s).
2. חשב את מספר ריינולדס באמצעות משוואה (1). בשביל זה, בהתחשב בקוטר המוט ( ) הנמדד בשלב 3.1, המהירות המתקרבת ( ) נקבעת עם משוואה (5), ואת הצמיגות הקינטמטית שנקבעה בשלב 4.3.1
קביעת מספר סטרוחאל: מערבולות בעקבות המוט נעות במהירות שונה כמו צירי הזמן בזרם החופשי. לפיכך, יש להעריך את תדירות שפיכת המערבולת באופן עצמאי.
1. הגדר הפניה קבועה במורד הזרם של המוט. הפניה זו יכולה להיות מחרוזת עדינה המחוברת לחלק החיצוני של המנהרה או קו דיגיטלי שנוסף לסרטון וידאו של תהליך הזרימה.
2. ספר את מספר מחזורי שפיכת המערבולת, חוצה את ההפניה במהלך פרק זמן מוגדר . מחזור שפיכת מערבולות מאויר באיור 2(א').
3. חשב את תדירות ההשלכה מהמשוואה הבאה:
4. השתמש בתוצאות משוואות (5) ו- (6) במשוואה (2) כדי לחשב את מספר סטרוהול.

Skip to...

0:07

Overview

0:55

Principles of Flow Separation

4:21

Producing Bubbles and Timelines in the Flow Facility

5:57

Setting up the Bluff Body

6:41

Studying and Analyzing the Von Karman Vortex Street

8:02

Representative Results

9:07

Applications

10:07

Summary

Videos from this collection:

article

Now Playing

הדמיה של זרימה בעבר גוף בלוף

Mechanical Engineering

11.9K Views

article

ציפה וגרירה על גופים שקועים

Mechanical Engineering

30.0K Views

article

יציבות של כלי שיט צפים

Mechanical Engineering

22.6K Views

article

הנעה ודחף

Mechanical Engineering

21.7K Views

article

רשתות צנרת והפסדי לחץ

Mechanical Engineering

58.1K Views

article

מרווה ומרתיח

Mechanical Engineering

7.7K Views

article

קפיצות הידראוליות

Mechanical Engineering

41.0K Views

article

ניתוח מחליף חום

Mechanical Engineering

28.0K Views

article

מבוא לקירור

Mechanical Engineering

24.7K Views

article

שושנת ים של חוט חם

Mechanical Engineering

15.6K Views

article

מדידת זרמים סוערים

Mechanical Engineering

13.5K Views

article

ג'ט פוגע בלוח נוטה

Mechanical Engineering

10.7K Views

article

שימור הגישה האנרגטית לניתוח מערכות

Mechanical Engineering

7.4K Views

article

מדידות של שימור המוני וקצב זרימה

Mechanical Engineering

22.6K Views

article

קביעת כוחות מניעה על לוח שטוח בשיטת אמצעי האחסון של הפקד

Mechanical Engineering

26.0K Views

Copyright © 2025 MyJoVE Corporation. All rights reserved