וקטורים בכיוונים מרובים
Overview
מקור: ניקולס טימונס, אסנטה קוריי, PhD, המחלקה לפיזיקה ואסטרונומיה, בית הספר למדעי הפיזיקה, אוניברסיטת קליפורניה, אירווין, קליפורניה
ניסוי זה מדגים כיצד וקטורים מוסיפים ומפחיתים בכיוונים מרובים. המטרה תהיה לחשב באופן אנליטי את התוספת או החיסור של וקטורים מרובים ולאחר מכן לאשר באופן ניסיוני את החישובים.
וקטור הוא עצם בעוצמה ובכיוון. הגודל של וקטור מסומן פשוט כאורך, בעוד הכיוון מוגדר בדרך כלל על ידי הזווית שהוא עושה עם ציר x. מכיוון שכוחות הם וקטורים, הם יכולים לשמש כייצוג פיזי של וקטורים. על ידי הקמת מערכת כוחות ומציאת הכוח הנוסף ייצור שיווי משקל בין הכוחות, ניתן לאמת מערכת וקטורים באופן ניסיוני.
Principles
באיור 1 מוצג הווקטור  , כמו גם את צירי x ו- yואת הזווית θ
, כמו גם את צירי x ו- yואת הזווית θ  שעושה עם ציר x.
שעושה עם ציר x.

איור 1.
כדי להוסיף או להחסיר שני וקטורים, כדאי לתאר את הווקטור במונחים של רכיבי x ו- yשלו. רכיב x הוא כמות הווקטור שמצביעה בכיוון x,המיוצג מתמטית כ:
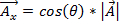 . (משוואה 1)
. (משוואה 1)
רכיב ה- yמיוצג כ:
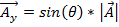 . (משוואה 2)
. (משוואה 2)
הגודל של  מוגדר להיות:
מוגדר להיות:
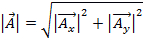 . (משוואה 3)
. (משוואה 3)
כדי להוסיף או להחסיר שני וקטורים, פשוט שברו את הווקטורים לרכיבי x ו- yשלהם ולאחר מכן הוסיפו או חיסרו, בהתאמה, את הרכיבים המתאימים.
לדוגמה, אם 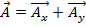 וקטור וקטור
וקטור וקטור 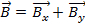 , אז התוספת של שני הווקטורים
, אז התוספת של שני הווקטורים  .
.
כדי לקבוע את הזווית ש-θ וקטור יוצר ביחס לציר x,השתמש במשוואה הבאה:
 . (משוואה 4)
. (משוואה 4)
מכיוון שלווקטורים יש גם גודל וגם כיוון, הכפלת שני וקטורים אינה פשוטה כמו הכפלת שני מספרים. ישנן שתי דרכים להכפיל וקטורים: מכפלת הנקודות והמכפלה הצולבת. ניתן לכתוב את מוצר הנקודה 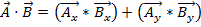 כ- או
כ- או 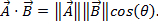 כאן, הזווית בין שני הווקטורים. לתוצאה יש רק סדר גודל, ולא כיוון. יישום של מכפלת הנקודות בפיזיקה הוא עבודה (W), שבה העבודה מוגדרת ככוח כפול מרחק
כאן, הזווית בין שני הווקטורים. לתוצאה יש רק סדר גודל, ולא כיוון. יישום של מכפלת הנקודות בפיזיקה הוא עבודה (W), שבה העבודה מוגדרת ככוח כפול מרחק 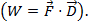 ניתן לכתוב את המכפלה הצולבת של שני וקטורים כמו
ניתן לכתוב את המכפלה הצולבת של שני וקטורים כמו 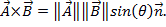 אמנם דומה למכפלת הנקודה, והמכפלה הצולבת מכילה את המונח
אמנם דומה למכפלת הנקודה, והמכפלה הצולבת מכילה את המונח  , המוגדר כווקטור עם גודל 1 המאונך לשני הווקטורים
, המוגדר כווקטור עם גודל 1 המאונך לשני הווקטורים  ו
ו  . התוצאה של המכפלה הצולבת היא וקטור. דוגמה אחת של המכפלה הצולבת בפיזיקה היא מומנט
. התוצאה של המכפלה הצולבת היא וקטור. דוגמה אחת של המכפלה הצולבת בפיזיקה היא מומנט  , שהוא תוצאה של כוח כפול רדיוס
, שהוא תוצאה של כוח כפול רדיוס 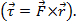
וקטורים שימושיים בפיזיקה מכיוון שכוחות כמו כוח המשיכה או החיכוך יכולים להיות מיוצגים כווקטורים. במעבדה זו, כוח הכבידה משמש להדגמת האופי הווקטורי של הכוחות וכיצד כוחות אלה מוסיפים בכיוונים מרובים. כוח הכבידה על פני כדור הארץ כתוב כ:
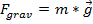 ,(משוואה 5)
,(משוואה 5)
 היכן מסת העצם, בעוד
היכן מסת העצם, בעוד  האצת הכבידה ליד פני כדור הארץ (9.8 מ'/ש'2).
האצת הכבידה ליד פני כדור הארץ (9.8 מ'/ש'2).
Procedure
1. כוחות איזון.
- על שולחן הכוח, הגדר שתי גלגלות עם אותה מסה הפונה לכיוונים מנוגדים (הבדל של 180° בזווית).
- הכוח של כל אחד מהם יהיה שווה
 ל. בדוק אם שני הכוחות שווים ומנוגדים על ידי בחינת הטבעת במרכז שולחן הכוח, אשר לא צריך לזוז.
ל. בדוק אם שני הכוחות שווים ומנוגדים על ידי בחינת הטבעת במרכז שולחן הכוח, אשר לא צריך לזוז. - שים לב שאם מרכיבי הווקטורים המשויכים לכוחות אלה מתווספים, לווקטור התוצאה יהיה אפס סדר גודל. כך ניתן לקבוע שכל הכוחות נמצאים בשיווי משקל.
2. חישובים אנליטיים.
- מעבדה זו תורכב משלושה כוחות בשיווי משקל. שני כוחות יהיו ידועים, בעוד השלישי יימצא אנליטי ראשון, באמצעות התיאוריה של וקטורים, ולאחר מכן באופן ניסיוני. עבור מעבדה זו, לשמור
 על 0° למשך הזמן.
על 0° למשך הזמן. - שים לב שאם

 ידועים
ידועים  ו, כאשר נוסף למערכת, גורם שני הכוחות להיות בשיווי משקל, אז
ו, כאשר נוסף למערכת, גורם שני הכוחות להיות בשיווי משקל, אז  הוא בסדר גודל שווה אבל בכיוון ההפוך לסכום ( +
הוא בסדר גודל שווה אבל בכיוון ההפוך לסכום ( + 
 ).
). - חישוב הגודל של

 ו. השתמש בעובדה
ו. השתמש בעובדה  ש- 1 ניוטון (N) היא יחידת כוח השווה ל
ש- 1 ניוטון (N) היא יחידת כוח השווה ל  - .
- . - באמצעות התיאוריה של וקטורים, לחשב מה סדר הגודל
 יהיה אם זה היה הסכום ( +
יהיה אם זה היה הסכום ( + 
 ).
). - באמצעות התיאוריה של וקטורים, לחשב איזו זווית
 תהיה אם זה היה הסכום ( +
תהיה אם זה היה הסכום ( + 
 ).
).
3. ניסוי.
- לאחר הערכים בשורה הראשונה של טבלה 1 עבור

 ו, הגדר את שני הכוחות בטבלת הכוח. זכור לשמור
ו, הגדר את שני הכוחות בטבלת הכוח. זכור לשמור  על 0°.
על 0°. - הגדר את הכוח השלישי,
 , על ידי הוספת משקולות ושינוי הזווית עד שיווי המשקל הוא הגיע. רשום ערכים אלה בטבלה 2.
, על ידי הוספת משקולות ושינוי הזווית עד שיווי המשקל הוא הגיע. רשום ערכים אלה בטבלה 2. - חזור על שלב 3.2 עבור כל אחד מארבעת המקרים.
- קבע את ההבדל באחוזים מהתוצאה האנליטית על-ידי חישוב
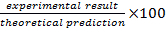 . השלם טבלה 2 עם ערכים מחושבים אלה.
. השלם טבלה 2 עם ערכים מחושבים אלה.
Results
תוצאות המעבדה מוצגות בטבלה 1 ובטבלה 2.
טבלה 1. ההתקנה.
| ההתקנה # | A | B | ||
| מסה | פינה | מסה | פינה | |
| 1 | 100 | 0 | 100 | 20 |
| 2 | 100 | 0 | 150 | 40 |
| 3 | 200 | 0 | 150 | 60 |
| 4 | 200 | 0 | 250 | 80 |
טבלה 2. תוצאות אנליטיות.
| ההתקנה # | גודל  (נ) |
גודל  (נ) |
פינה  (°) |
גודל  (נ) |
פינה  (°) |
| 1 | 0.98 | 0.98 | 20 | 1.93 | 10 |
| 2 | 0.98 | 1.47 | 40 | 2.31 | 24 |
| 3 | 1.96 | 1.47 | 60 | 2.98 | 25 |
| 4 | 1.96 | 2.45 | 80 | 3.39 | 45 |
טבלה 3. תוצאות ניסוי.
| ההתקנה # | סדר גודל ניסיוני  (נ) |
סדר גודל אנליטי  (נ) |
הבדל (%) |
זווית ניסיונית  (°) |
זווית אנליטית (°) |
הבדל (%) |
| 1 | 2.1 | 1.93 | 9 | 11 | 10 | 10 |
| 2 | 2.2 | 2.31 | 5 | 26 | 24 | 8 |
| 3 | 2.8 | 2.98 | 6 | 28 | 25 | 12 |
| 4 | 3.5 | 3.39 | 3 | 43 | 45 | 5 |
תוצאות הניסוי עולות בהסכמה עם החישובים האנליטיים. ניתן לחשב את הסכום של שני וקטורים ואת הזווית ביניהם באמצעות משוואות 1-5. המשוואות תקפות לביצוע חישובים של וקטורים פיזיים, כגון כוח.
Application and Summary
שחקן חוץ בבייסבול צריך להבין וקטורים כדי לתפוס כדור בתנועה. אם שחקן החוץ רק ידע את מהירות הכדור, הוא היה רץ למגרש השמאלי במקום ימינה ומפספס את הכדור. אם הוא רק היה יודע את כיוון הפגיעה, הוא היה יכול להסתער פנימה, רק כדי לראות את הכדור מפליג מעל ראשו. אם הוא מבין וקטורים, אז ברגע שהכדור נפגע, הוא יכול לשקול גם את הגודל וגם את הכיוון כדי להעריך איפה הכדור הולך להיות כשהוא תופס.
כאשר מטוס נמצא בשמיים, המהירות והכיוון שלו יכולים להיכתב כווקטור. כאשר יש רוח כבדה, וקטור הרוח מוסיף לווקטור של המישור כדי לתת את וקטור המערכת המתקבל. לדוגמה, אם מטוס טס לתוך הרוח, הגודל של הווקטור המתקבל יהיה קטן מהגודל ההתחלתי. זה מתאים למטוס נע לאט יותר כאשר הוא פונה אל הרוח, וזה הגיוני אינטואיטיבית.
כאשר שני עצמים מתנגשים ונדבקים זה בזה, ניתן להעריך את התנע הסופי שלהם (וקטור) כסכום של שני וקטורי התנע ההתחלתיים. זהו פישוט, כמו בעולם האמיתי, לשני עצמים מתנגשים יש גורמים נוספים לשקול, כמו חום או עיוות מההתנגשות. מומנטום הוא רק המסה של עצם כפול המהירות שלו. אם שני מחליקים על קרח נעים בכיוונים שונים ובמהירויות שונות מתנגשים ונאחזים זה בזה, ניתן להעריך את הכיוון והמהירות הסופיים שלהם בהתבסס על הרכיבים הווקטוריים הראשוניים שלהם.
בניסוי זה, האופי הווקטורי של הכוחות נבדק ונמדד. וקטורים נוספו יחד, והגודל והכיוון הנובעים מכך נקבעו הן מבחינה אנליטית והן מבחינה ניסיונית.
Tags
Skip to...
Videos from this collection:

Now Playing
וקטורים בכיוונים מרובים
Physics I
182.3K Views

חוקי התנועה של ניוטון
Physics I
75.7K Views

כוח ותאוצה
Physics I
79.1K Views

קינמטיקה ותנועת קליעים
Physics I
72.6K Views

חוק הכבידה האוניברסלית של ניוטון
Physics I
190.8K Views

שימור המומנטום
Physics I
43.3K Views

חיכוך
Physics I
52.9K Views

חוק הוק ותנועה הרמונית פשוטה
Physics I
61.3K Views

שיווי משקל ודיאגרמות גוף חופשי
Physics I
37.3K Views

מומנט
Physics I
24.3K Views

אינרציה סיבובית
Physics I
43.5K Views

מומנטום זוויתי
Physics I
36.2K Views

אנרגיה ועבודה
Physics I
49.7K Views

אנטלפיה
Physics I
60.4K Views

אנטרופיה
Physics I
17.6K Views
Copyright © 2025 MyJoVE Corporation. All rights reserved