Moment angulaire
Vue d'ensemble
Source : Nicholas Timmons, Antonella Cooray, Ph.d., département de physique & astronomie, école de Sciences physique, University of California, Irvine, CA
Angular momentum est défini comme le produit de l’inertie et la vitesse angulaire de l’objet. Comme son analogue linéaire, angulaire est conservé, ce qui signifie que le moment angulaire total d’un système ne changera pas s’il n’y a aucun couples externes sur le système. Un couple est l’équivalent de rotation d’une force. Parce que c’est un conservée, moment angulaire est une quantité importante en physique.
L’objectif de cette étude est de mesurer le moment angulaire d’une tige rotative et à la conservation du moment cinétique permet d’expliquer deux démonstrations de rotationnels.
Principles
Moment angulaire peut être écrite comme :
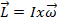 , (Équation 1)
, (Équation 1)
où 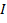 est le moment d’inertie et
est le moment d’inertie et  est la vitesse angulaire. Le moment d’inertie est l’analogue de rotation de la masse pour mouvement linéaire. Elle est liée à la distribution massive d’un objet en rotation et l’axe de rotation. Plus le moment d’inertie, le couple est nécessaire pour provoquer une accélération angulaire sur un objet. La règle de droite peut être utilisée pour déterminer la direction du moment cinétique. Lorsque les doigts de la main droite enroulent dans le sens de rotation, les points de pouce étendu dans la direction du moment cinétique.
est la vitesse angulaire. Le moment d’inertie est l’analogue de rotation de la masse pour mouvement linéaire. Elle est liée à la distribution massive d’un objet en rotation et l’axe de rotation. Plus le moment d’inertie, le couple est nécessaire pour provoquer une accélération angulaire sur un objet. La règle de droite peut être utilisée pour déterminer la direction du moment cinétique. Lorsque les doigts de la main droite enroulent dans le sens de rotation, les points de pouce étendu dans la direction du moment cinétique.
Un couple est défini comme le produit d’une force appliquée à une certaine distance de l’axe de rotation :
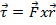 , (Équation 2)
, (Équation 2)
où 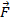 est la force exercée et
est la force exercée et 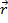 est la distance à l’axe de rotation. Si un couple agit sur un objet, la vitesse angulaire de cet objet change, ainsi que son moment angulaire. Si la somme des couples de serrage sur un objet est égale à zéro, alors le moment angulaire total seront conservé et auront la même valeur finale comme c’était le cas initialement.
est la distance à l’axe de rotation. Si un couple agit sur un objet, la vitesse angulaire de cet objet change, ainsi que son moment angulaire. Si la somme des couples de serrage sur un objet est égale à zéro, alors le moment angulaire total seront conservé et auront la même valeur finale comme c’était le cas initialement.
Un amusant exemple de la conservation du moment angulaire peut être démontré avec une roue de vélo et une présidence tournante. La roue et la personne à la présidence constituent un système avec un moment angulaire. Si une personne demande un couple pour faire tourner la roue, avec l’axe pointant verticalement, le système sera ont gagné angulaire. Si la personne renverse alors le rouet, elle commencera à tourner sur sa chaise dans le sens inverse de la roue qui tourne. Ici, le système avait angulaire, avec son orientation déterminée par la règle de droite. Lorsque la roue a été renversée, le moment cinétique du système changea de direction. En raison de la conservation, la présidence a commencé à tourner dans le sens inverse pour que le moment cinétique total du système est égal à celle du système avant que la roue a été renversée.
Une autre démonstration de la conservation du moment angulaire peut être faite avec une chaise de filature et de deux graisses. Si les poids sont tendit à bout de bras, tandis que le Président est en rotation et sont ensuite présentées près de la poitrine, il y aura une augmentation de la vitesse angulaire. Cela arrive parce que ce qui porte les poids plus près de l’axe de rotation diminue le moment d’inertie du système. S’il n’y a pas plus de force agissant pour faire tourner le fauteuil, puis le couple exercé sur le système est nulle. Le moment angulaire doit rester constant, car il n’y a aucun couple, et le seul moyen pour cela est de la vitesse angulaire d’augmenter.
Dans cette expérience, une tige rotative est reliée à une masse tombante. La masse tombante fournira un couple sur la tige, et le moment angulaire sera mesuré à deux points : premièrement quand le poids est tombé à mi-chemin et là encore une fois le poids atteint la fin de la chaîne. Voir la Figure 1 pour une image de l’installation expérimentale.
Le moment d’inertie d’une canne est 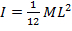 , où
, où 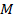 est la masse de la tige et
est la masse de la tige et 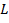 est la longueur. Ces quantités peuvent être mesurées avant que l’expérience ait lieu. Pour trouver la vitesse angulaire
est la longueur. Ces quantités peuvent être mesurées avant que l’expérience ait lieu. Pour trouver la vitesse angulaire  , les équations cinématiques rotationnels seront utilisées :
, les équations cinématiques rotationnels seront utilisées :
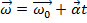 . (Équation 3)
. (Équation 3)
Équation 3 indique que la vitesse angulaire finale  est égale à la vitesse angulaire initiale
est égale à la vitesse angulaire initiale  plus l’accélération angulaire
plus l’accélération angulaire 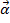 , multiplié par le temps. Parce que la tige va commencer au repos,
, multiplié par le temps. Parce que la tige va commencer au repos,  sera égale à zéro. L’accélération angulaire
sera égale à zéro. L’accélération angulaire 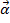 est définie par
est définie par 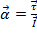 , où
, où 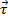 est le couple et
est le couple et 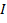 est le moment d’inertie. Le couple est la force du poids provoquant une tension dans la chaîne, ce qui provoque la tige faire pivoter, multiplié par la distance entre la force et l’axe de rotation :
est le moment d’inertie. Le couple est la force du poids provoquant une tension dans la chaîne, ce qui provoque la tige faire pivoter, multiplié par la distance entre la force et l’axe de rotation : 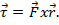 que la force agissant sur la poulie est égale à la force du poids :
que la force agissant sur la poulie est égale à la force du poids : 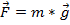 , où
, où 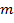 est la masse et
est la masse et 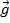 est l’accélération due à la pesanteur. Le rayon
est l’accélération due à la pesanteur. Le rayon 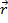 du couple sera la distance entre la chaîne de la plaie et l’axe de rotation.
du couple sera la distance entre la chaîne de la plaie et l’axe de rotation.

Figure 1. Montage expérimental. Médaillon : stand 1) grand anneau, extendeur 2), Assemblée 3) rotative, 4) poids et couple 5) bar.
Procédure
1. vérifier la théorie de la conservation du moment angulaire avec la roue de vélo.
- Alors qu’il est assis sur une chaise qui peut tourner librement, commencer à tourner la roue de vélo et puis maintenez-le par les poignées ainsi que sa direction du moment cinétique est verticale.
- Tout en tenant le volant par les deux poignées, retournez la roue pour que son moment CINETIQUE pointe dans la direction opposée. Remarquez comment la présidence commencera à tourner.
2. vérifier la théorie de la conservation du moment angulaire avec deux poids.
- Assis dans un fauteuil qui peut tourner librement, tends deux poids de dépendance.
- Avoir un partenaire obtenir la filature de la chaise et ensuite rapprocher les poids la poitrine. Remarquez l’augmentation de la vitesse de rotation de la présidence.
3. mesurer la variation du moment angulaire dans la canne.
- Mesurer la longueur de la tige et de sa masse. À l’aide d’un bâton de compteur, mesurer le point à mi-chemin de la masse tombante et marquer le faisceau vertical avec du ruban adhésif afin d’avoir une référence. Calculer le moment d’inertie de la tige.
- Ajouter 200 g à la fin de la chaîne et l’enrouler jusqu’au sommet. Prenez note d’où se trouve le point à mi-chemin de la chaîne.
- Le poids de sortie et de mesurer la quantité de temps qu’il faut se pour rendre à mi-chemin, puis à nouveau vers le bas. Faire cela trois fois et prendre les valeurs moyennes. Calculer le moment angulaire aux deux points.
- Augmenter le poids à la fin de la chaîne à 500 g et répétez l’étape 3.3.
- Augmenter le poids à 1 000 g et répétez l’étape 3.3.
Résultats
| Messe (g) |
Angular momentum à mi-chemin (kg m2) /s |
Moment cinétique en bas (kg m2) /s |
Différence (kg m2) /s |
| 200 | 0,41 | 0,58 | 0,17 |
| 500 | 0,66 | 0,91 | 0.25 |
| 1 000 | 0,93 | 1.32 | 0,39 |
Dans la première étape, la théorie de la conservation du moment angulaire a été confirmée, que le Président a commencé à tourner quand la roue a été basculée. À l’étape deux, la théorie de la conservation du moment angulaire a été confirmée à nouveau, que le Président a commencé à tourner plus vite quand les poids ont été amenés pour le moment d’inertie du système est réduite. Dans la troisième étape du laboratoire, l’augmentation du couple sur la canne a augmenté le moment angulaire. Avec toutes les autres quantités étant constant, le moment angulaire augmente linéairement avec le temps.
Applications et Résumé
Tout comme dans la partie de chaise de filature du laboratoire, changer le moment d’inertie d’un objet peut augmenter ou diminuer la vitesse angulaire de cet objet. Les patineurs artistiques profiter de cette commençant parfois à pédaler avec les bras tendus et puis rapprochent leurs armes leur corps, qui vont les faire tourner beaucoup plus rapidement.
Pourquoi est-il plus facile d’équilibre sur un vélo lorsque celui-ci est en mouvement ? La réponse est angulaire. Quand les roues ne tournent pas, il est facile pour le vélo à tomber. Une fois que les roues sont en mouvement, ils auront certains montant du moment angulaire. Plus le moment angulaire, le couple est nécessaire pour le changer, il est donc difficile de basculer la moto.
Si un quart-arrière du football à lève sans mettre aucun spin sur la balle, son vol sera bancal et pourrait manquer sa cible. Pour éviter cela, quarts utilisent leurs doigts pour obtenir le football tournante quand ils le jeter. Lorsque la balle tourne comme il vole dans les airs, il a le moment cinétique, qui exige le couple de changer l’orientation du moment angulaire. La balle ne sera pas vaciller ou de retourner dans l’air.
Dans cette expérience, le concept de la conservation du moment a été testé dans deux manifestations. Dans l’une, la direction du moment cinétique a été conservée, et dans l’autre, la magnitude a été conservée. Dans la dernière partie de l’expérience, l’effet d’un couple sur moment cinétique a été mesurée.
Passer à...
Vidéos de cette collection:

Now Playing
Moment angulaire
Physics I
36.2K Vues

Les lois du mouvement de Newton
Physics I
75.7K Vues

Force et accélération
Physics I
79.1K Vues

Vecteurs dans de multiples Directions
Physics I
182.3K Vues

Cinématique et mouvement du projectile
Physics I
72.6K Vues

La loi de l'attraction universelle de Newton
Physics I
190.8K Vues

Conservation du mouvement
Physics I
43.3K Vues

Frottement
Physics I
52.9K Vues

Loi de Hooke et mouvement harmonique simple
Physics I
61.3K Vues

Équilibre et diagrammes de corps libre
Physics I
37.3K Vues

Moment d'une force
Physics I
24.3K Vues

Inertie de rotation
Physics I
43.5K Vues

Énergie et travail d'une force
Physics I
49.7K Vues

Enthalpie
Physics I
60.4K Vues

Entropie
Physics I
17.6K Vues