Enfoque de conservación de la energía para el análisis de sistemas
Visión general
Fuente: Ricardo Mejía-Alvarez y Hussam Hikmat Jabbar, Departamento de ingeniería mecánica, Universidad Estatal de Michigan, East Lansing, MI
El propósito de este experimento es demostrar la aplicación de la ecuación de conservación de energía para determinar el rendimiento de un sistema de flujo. Para ello, se aplica la ecuación de energía para flujo incompresible, estable a un tubo corto con una válvula de compuerta. Poco a poco entonces se cierra la válvula de puerta y su influencia en las condiciones de flujo se caracteriza. Además, se estudia la interacción entre este sistema de flujo y el ventilador que impulsa el flujo mediante la comparación de la curva del sistema con la curva característica del ventilador.
Este experimento ayuda a entender como disipación de la energía utiliza válvulas para restringir el flujo. También, bajo el mismo principio, este experimento ofrece un método simple para medir el caudal con el cambio de presión a través de una entrada fuerte.
Principios
Análisis de flujo de fluidos con frecuencia realiza en base a qué energía se transforma como el líquido fluye a través de un sistema. La energía total por un flujo incluye energía cinética, potencial y termodinámica. Estas formas de energía pueden transformar en uno a libremente, y la energía contenida en el flujo en una determinada posición en un sistema de flujo es el equilibrio entre la energía entrante total, la energía adicional y la resta energía. Este balance de energía puede ser expresada en forma de ecuación como sigue [1, 2]:
 (1)
(1)
Aquí, los subíndices 1 y 5 refieren a las condiciones de entrada y salida del sistema de flujo respectivamente. La figura 2 muestra un esquema del sistema de flujo: el aire entra a través de un flujo de sistema, o contracción, llamado pleno de acondicionamiento (su descarga se muestra en la figura 3. Luego, pasa a un tubo corto con una válvula en su extremo (ver figura 2 (b) para obtener detalles sobre el sistema de la válvula de la pipa y figuras 2 (a) y (B) para los cuadros). El aire se descarga de la válvula en un espacio cerrado, aislado del exterior llamado "receptor" (ver figura 3 para referencia). Como se muestra en la figura 3, el receptor es lo suficientemente grande como para albergar el sistema de adquisición de datos y los experimentalistas. Finalmente, el flujo sale del receptor a través de una placa perforada que sirve como un amortiguador para regulación de flujo (ver figura 3 para referencia). El aire es capturado por un ventilador centrífugo que descarga a la atmósfera. Los términos entre paréntesis representan el contenido en energía específico en cada puerto, que es la suma de energía potencial gravitatoria  , energía cinética
, energía cinética 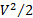 y termodinámica (o potencial de presión) energía
y termodinámica (o potencial de presión) energía  . El coeficiente de
. El coeficiente de  se utiliza para tomar en cuenta la forma del perfil de velocidad. Para el presente experimento
se utiliza para tomar en cuenta la forma del perfil de velocidad. Para el presente experimento 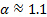 porque el flujo es turbulento [1, 2]. Como tal, el lado izquierdo de la ecuación (1) representa el cambio en el contenido de energía entre los puertos de entrada y salida. En la ausencia de efectos disipativos o trabajo externo, esta diferencia es cero. Sin embargo, la mayoría aplicaciones de ingeniería que implican flujos reales incluyen adición o substracción de energía por medio de máquinas de flujo,
porque el flujo es turbulento [1, 2]. Como tal, el lado izquierdo de la ecuación (1) representa el cambio en el contenido de energía entre los puertos de entrada y salida. En la ausencia de efectos disipativos o trabajo externo, esta diferencia es cero. Sin embargo, la mayoría aplicaciones de ingeniería que implican flujos reales incluyen adición o substracción de energía por medio de máquinas de flujo, y los efectos disipativos,
y los efectos disipativos, . Estos dos efectos se incluyen en la parte derecha de la ecuación (1).
. Estos dos efectos se incluyen en la parte derecha de la ecuación (1).
En este experimento, se utilizará un ventilador centrífugo para inducir el flujo, es decir, al agregar energía al líquido. Para este tipo de máquina, el término  es una función de la velocidad de flujo
es una función de la velocidad de flujo  llamada curva característica y se determina experimentalmente:
llamada curva característica y se determina experimentalmente:
 (2)
(2)
Aquí, 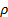 y
y  son la densidad y la viscosidad cinemática del aire en las condiciones locales, y
son la densidad y la viscosidad cinemática del aire en las condiciones locales, y 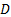 es el diámetro del sistema de flujo (
es el diámetro del sistema de flujo ( m m en el presente experimento). Ecuación (2) está en una forma que asegura que las constantes en el primer y segundo término son sin dimensiones, mientras que la constante en el tercer término es en unidades de presión (Pa) para asegurar la homogeneidad dimensional. Ecuación (2) es la "curva de rendimiento de ventilador" se muestra en la figura 1.
m m en el presente experimento). Ecuación (2) está en una forma que asegura que las constantes en el primer y segundo término son sin dimensiones, mientras que la constante en el tercer término es en unidades de presión (Pa) para asegurar la homogeneidad dimensional. Ecuación (2) es la "curva de rendimiento de ventilador" se muestra en la figura 1.
Por último, la disipación de la energía es proporcional a la energía cinética del flujo:
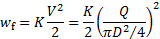 (3)
(3)
Tenga en cuenta que, utilizando la ecuación de continuidad ( , donde
, donde 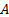 es el área transversal [1, 2]), la disipación de la energía también se puede escribir en términos de la tasa de flujo,
es el área transversal [1, 2]), la disipación de la energía también se puede escribir en términos de la tasa de flujo, . Figura 1 se presenta esta última forma de la ecuación (3) como la "curva de sistema de flujo". En la ecuación (3), el coeficiente de proporcionalidad
. Figura 1 se presenta esta última forma de la ecuación (3) como la "curva de sistema de flujo". En la ecuación (3), el coeficiente de proporcionalidad  , se llama el coeficiente de pérdida y es la adición de efectos disipativos inducida por los elementos del sistema como resultado de las interacciones viscosos flujo. Mientras que las contribuciones de tuberías y conductos dependen de la rugosidad, longitud y número de Reynolds, la contribución de instalaciones de tuberías, entradas y descargas, expansiones, contracciones, curvas y válvulas depende de sus geometrías particulares. Para el presente experimento, el coeficiente global de pérdidas es la combinación de una entrada, una válvula y una descarga:
, se llama el coeficiente de pérdida y es la adición de efectos disipativos inducida por los elementos del sistema como resultado de las interacciones viscosos flujo. Mientras que las contribuciones de tuberías y conductos dependen de la rugosidad, longitud y número de Reynolds, la contribución de instalaciones de tuberías, entradas y descargas, expansiones, contracciones, curvas y válvulas depende de sus geometrías particulares. Para el presente experimento, el coeficiente global de pérdidas es la combinación de una entrada, una válvula y una descarga:
 (4)
(4)
Donde los valores de los coeficientes de pérdida para la entrada y la descarga son 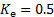 y
y  respectivamente (ver [1, 2] para referencia). El coeficiente de pérdida de la válvula,
respectivamente (ver [1, 2] para referencia). El coeficiente de pérdida de la válvula,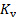 , se discutirá en la siguiente sección.
, se discutirá en la siguiente sección.
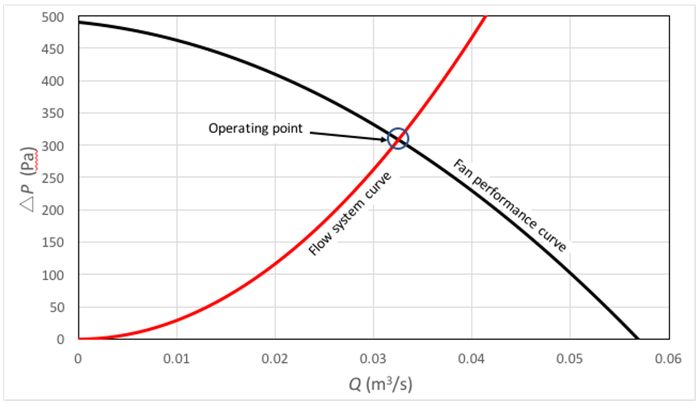
Figura 1. Ejemplo de curva del sistema y la curva de rendimiento ventilador.  : curva de sistema;
: curva de sistema;  : curva de rendimiento del ventilador. El círculo azul destaca la intersección entre ambas curvas, que es el punto operativo.
: curva de rendimiento del ventilador. El círculo azul destaca la intersección entre ambas curvas, que es el punto operativo.

Figura 2. Ajuste experimental. (A): centro del flujo. El flujo se mueve del de izquierda a derecha, entra el pleno a través de un flujo acondicionamiento sección, luego fluye a través de la tubería y la válvula, vertidos dentro del receptor y finalmente salga el sistema a través del ventilador. (B): detalles de los equipos de adquisición de datos y sistema de flujo. Por favor haga clic aquí para ver una versión más grande de esta figura.

Figura 3. Sistema de adquisición de datos. (A) las conexiones de estos dispositivos de adquisición de datos siguen el diagrama en la figura 2 (b). (B) virtual interfaz para adquisición de datos (escrito en LabView). Haga clic aquí para ver una versión más grande de esta figura.
Características de la disipación de una válvula de
Puesto que las válvulas son esencialmente dispositivos de geometría variable, su coeficiente de pérdida específica es una función del ángulo de rotación de su eje ( ). Con esto en mente,
). Con esto en mente,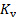 varía a medida que la válvula se abre o cierra según la siguiente relación:
varía a medida que la válvula se abre o cierra según la siguiente relación:
 (5)
(5)
Aquí, utilizamos la ecuación de continuidad una vez más para expresar el coeficiente de pérdida en términos de la tasa de flujo. Además, la ecuación (5) sugiere que podemos determinar el coeficiente de pérdida de la válvula por conocer el valor de la tasa de flujo y la caída de presión a través de la válvula en función de la abertura del ángulo y caudal: . Esta es también la diferencia de presión entre los puntos 3 y 4 en la figura 2 (b) (
. Esta es también la diferencia de presión entre los puntos 3 y 4 en la figura 2 (b) ( ).
).
Punto de funcionamiento
Como se muestra en la figura 1, el punto de funcionamiento de un sistema de flujo impulsado por una máquina de flujo, como la que aparece en este experimento, está dada por el punto de intersección de la curva característica del ventilador y la curva de flujo-sistema. Este punto puede ser caracterizado mediante la ecuación de energía como sigue: como puede verse en la figura 2, el aire entra en el sistema de flujo de una gran sala en condiciones atmosféricas y las salidas a la misma habitación sin cambios significativos en la altura. En consecuencia, la presión, velocidad y altura condiciones en entrada y salida del sistema (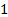 y
y  subíndices en la ecuación (1) respectivamente) son idénticos y cancelar entre sí. En consecuencia, la energía Añadida por el ventilador es balanceada por la energía disipada por el sistema de flujo. En otras palabras, las ecuaciones (2) y (3) formar una igualdad que se traduce en la relación siguiente después de simplificación:
subíndices en la ecuación (1) respectivamente) son idénticos y cancelar entre sí. En consecuencia, la energía Añadida por el ventilador es balanceada por la energía disipada por el sistema de flujo. En otras palabras, las ecuaciones (2) y (3) formar una igualdad que se traduce en la relación siguiente después de simplificación:
 (6)
(6)
La raíz positiva de esta ecuación expresa el punto de funcionamiento:
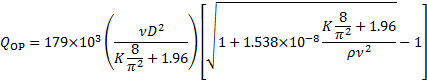 (7)
(7)
Aquí, el subíndice "OP" significa "Punto de funcionamiento". El coeficiente de pérdida en la ecuación (7) es la suma de los coeficientes de pérdida de la entrada, la válvula y la descarga. De las ecuaciones (4) y (5):
 (8)
(8)
Medición de caudal
Análogo a todos los análisis anteriores, la ecuación (1) se aplica entre el pleno y un punto aguas abajo de la entrada fuerte (puntos 2 y 3 en la figura 2(B)) para recuperar la siguiente ecuación:
 (9)
(9)
Aquí, utilizamos el hecho de que no hay ningún cambio en altura entre los puntos 2 y 3, y la velocidad dentro de la cámara es insignificante. Introduciendo la ecuación de continuidad (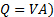 y la ecuación (3), llegamos a la siguiente relación para la velocidad de flujo en términos de la diferencia de presión entre la cámara (punto 2 en la figura 2(B)) y la presión estática corriente arriba de la válvula (punto 3 en la figura 2 (B)):
y la ecuación (3), llegamos a la siguiente relación para la velocidad de flujo en términos de la diferencia de presión entre la cámara (punto 2 en la figura 2(B)) y la presión estática corriente arriba de la válvula (punto 3 en la figura 2 (B)):
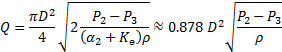 (10)
(10)
La constante 0.878 se obtiene tras sustituir los valores de la corrección de la velocidad y coeficiente de pérdida (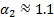 y
y 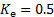 , ver [1, 2] para la referencia) y agrupar todas las constantes en una sola.
, ver [1, 2] para la referencia) y agrupar todas las constantes en una sola.
Procedimiento
1. configuración de la instalación
- Asegúrese de que el ventilador no está funcionando, por lo que no hay flujo en la instalación.
- Verificar que el sistema de adquisición de datos (figura 4(A)) sigue el esquema en la figura 2B.
- Conecte el positivo del transductor de presión #1 (ver figura 2B para la referencia) para la toma de presión aguas arriba de la válvula (
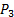 ).
). - Salir del puerto negativo del transductor de presión #1 abierto a las condiciones de habitación (receptor:
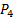 ). Por lo tanto, la lectura de este transductor será directamente
). Por lo tanto, la lectura de este transductor será directamente  .
. - Conecte el puerto positivo del transductor de presión #2 (ver figura 2B para la referencia) al grifo de presión plenum (
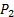 ).
). - Conecte el puerto negativo del transductor de presión #2 (ver figura 2B para referencia) a la toma de presión aguas arriba de la válvula (
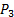 ). Por lo tanto, la lectura de este transductor será directamente
). Por lo tanto, la lectura de este transductor será directamente , como es requerido por la ecuación (10).
, como es requerido por la ecuación (10).
- Conecte el positivo del transductor de presión #1 (ver figura 2B para la referencia) para la toma de presión aguas arriba de la válvula (
- Asegúrese de que el canal virtual 0 en el sistema de adquisición de datos (figura 4B) corresponde a transductor de presión #1 (
 ) y el canal virtual 1 corresponde al transductor de presión #2 (
) y el canal virtual 1 corresponde al transductor de presión #2 ( ).
). - Establecer el sistema de adquisición de datos a la muestra a una frecuencia de 100 Hz para un total de 500 muestras (es decir, 5s de datos).
Tabla 1. Parámetros básicos para el estudio experimental.
|
Parámetro |
Valor |
| Diámetro de la tubería (D) | 50.8 mm (2 pulgadas) |
| Constante de calibración del transductor #1 (m_p1) |
|
| Constante de calibración del transductor #2 (m_p2) |
|
| Presión atmosférica local | 100,474.15 Pa |
| Temperatura local | 297.15 K |
| Densidad del aire local | 1,186 kg/m3 |

Figura 4 . Facilidad de flujo. (A): vista del plenum de descarga en la sección del receptor antes de instalar el conjunto de válvulas que se estudiará. (B): tres tipos de válvulas dentro del receptor. De izquierda a derecha: puerta, válvula de globo, válvula de mariposa. (C): salida de los puertos del receptor. Las válvulas de descargan del flujo dentro del receptor, y el ventilador succiona el flujo que sale del receptor a través de la placa perforada en la imagen. Haga clic aquí para ver una versión más grande de esta figura.
2. las medidas
- El diámetro de la tubería conectada a la válvula y calcular su área transversal.
- Determinar el número máximo de vueltas completas de la palanca necesaria para mover la válvula desde la posición totalmente cerrada a la posición completamente abierta. Si este número no es entero, excluir la última rotación fraccional para simplificar este análisis. Para el experimento actual, el número máximo de vueltas completas es 12.
- Cerrar la válvula completamente.
- Gire la manija de la válvula hasta que esté completamente abierta mientras que el número de vueltas completas. Para simplificar, utilice sólo un número entero de vueltas para el experimento. Por ejemplo, tarda aproximadamente 12 vueltas y 1/3 de giro para abrir completamente la válvula que se usa en este experimento. Por lo tanto, vamos a girar el mango de esta válvula sólo 12 vueltas completas desde su posición totalmente cerrada y que definen como la posición inicial (
 ).
). - Encienda la facilidad de flujo.
- Utilizar el sistema de adquisición de datos para registrar las lecturas de
 y
y  .
. - Entrar en la tabla 2 los valores medios de
 y
y  obtenido con el sistema de adquisición de datos.
obtenido con el sistema de adquisición de datos. - Cierre la válvula de 1,5 vueltas.
- Repita los pasos del 2.6 a 2.8 hasta tabla 2 está totalmente poblada.
- Apague la facilidad de flujo.
3. Análisis de los datos
- Determinar el coeficiente de pérdida de la válvula para cada posición angular utilizando la ecuación (5). Introduzca estos valores en la tabla 2.
- Determinar el caudal para cada posición angular de la válvula usando la ecuación (10). Introduzca estos valores en la tabla 2.
- Determinar el punto de funcionamiento usando la ecuación (7). Introduzca estos valores en la tabla 2.
- Calcular la diferencia relativa entre el caudal medido y el punto de operación
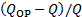
- Utilizar la ecuación (3) para producir un diagrama de las curvas del sistema para todos los valores de
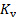 . Considerar el coeficiente de pérdida total como
. Considerar el coeficiente de pérdida total como  .
. - Añadir la curva característica del ventilador a este mismo terreno usando la ecuación (2).
Tabla 2. Resultados representativos. Mediciones de diferencias de presión y estimación de coeficientes de velocidad y pérdida de flujo.
| [P_pl-P_a] (Pa) | [P_a-P_r] (Pa) | Q (m3/s) | K | Q_OP (m3/s) | Ε (%) |
| 246.75 | 54.00 | 0.0327 | 0.450 | 0.0316 | -3.16 |
| 208.62 | 114.22 | 0.0301 | 0.976 | 0.0293 | -2.51 |
| 156.19 | 204.80 | 0.0260 | 2.198 | 0.0254 | -2.30 |
| 109.30 | 281.69 | 0.0218 | 4.224 | 0.0214 | -1.53 |
| 71.82 | 348.38 | 0.0176 | 7.863 | 0.0174 | -1.26 |
| 38.72 | 408.60 | 0.0129 | 16.989 | 0.0128 | -0,90 |
| 15.00 | 452.39 | 0.0081 | 48.359 | 0.0080 | -0,32 |
| 2.51 | 482.50 | 0.0033 | 307.799 | 0.0033 | -0,18 |
Resultados
La figura 5 muestra los resultados de las mediciones actuales. Aquí, la línea sólida negra se generó con la ecuación (2) y cada línea roja con la ecuación (3) para diferentes valores del coeficiente de pérdida de la válvula. De la figura, es evidente que la curva del sistema aumenta su pendiente como se cierra la válvula. En otras palabras, este experimento demuestra que el principio detrás de la operación de una válvula aumentar la disipación de la energía para limitar el flujo. Por otra parte, de la ecuación (5), se podría inferir que el valor de 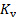 se convierte en infinito cuando la válvula está completamente cerrada. Conceptualmente, esta condición significa que la energía se disipa, por lo tanto totalmente impidiendo el flujo a través de la válvula.
se convierte en infinito cuando la válvula está completamente cerrada. Conceptualmente, esta condición significa que la energía se disipa, por lo tanto totalmente impidiendo el flujo a través de la válvula.
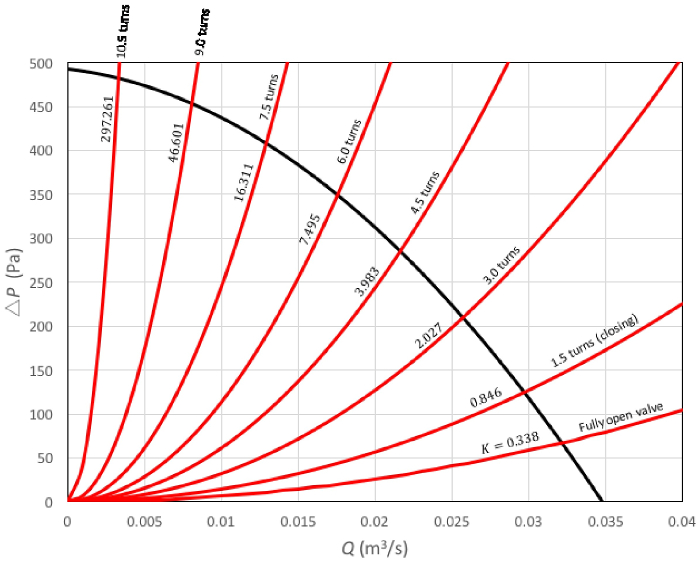
Figura 5 . Resultados representativos.  : curvas del sistema. Cada curva de esta familia es el resultado de diferentes grados de apertura de la válvula. La pendiente de las curvas aumenta a medida que la válvula está cerrada. Cada curva tiene su coeficiente de pérdida correspondiente para referencia;
: curvas del sistema. Cada curva de esta familia es el resultado de diferentes grados de apertura de la válvula. La pendiente de las curvas aumenta a medida que la válvula está cerrada. Cada curva tiene su coeficiente de pérdida correspondiente para referencia;  : curva de rendimiento del ventilador. Haga clic aquí para ver una versión más grande de esta figura.
: curva de rendimiento del ventilador. Haga clic aquí para ver una versión más grande de esta figura.
Como se muestra en la tabla 2, el error entre el caudal estimado en el punto de trabajo (ecuación (7)) y el caudal medido (ecuación (10)) se mantiene por debajo de 3.2% para el rango estudiado de caudales. Aunque esto es un resultado satisfactorio, dado el pequeño porcentaje de error, el caudal estimado en el punto de funcionamiento siempre se subestima y sigue una tendencia decreciente como poco a poco se cierra la válvula. Esta tendencia ofrece cierta penetración en el comportamiento del sistema de flujo, sobre todo porque el valor de la corrección del factor de velocidad falta de uniformidad aumenta ligeramente con el número de Reynolds. Por lo tanto no es sorprendente que el error aumenta con la velocidad de flujo.
aumenta ligeramente con el número de Reynolds. Por lo tanto no es sorprendente que el error aumenta con la velocidad de flujo.
Aplicación y resumen
Este experimento explora la aplicación de la ecuación de energía para caracterizar la acción de una válvula de flujo de la tubería. Se observó que la válvula induce la resistencia al flujo al aumentar la disipación de la energía. Considerando que la caída de presión en el sistema de flujo es directamente proporcional al cuadrado de la velocidad de flujo, el efecto de la disipación de la energía es capturado por la magnitud del coeficiente de proporcionalidad. Este coeficiente es la suma de los coeficientes de pérdida de todos los elementos en el sistema de flujo, incluyendo la válvula. El coeficiente de pérdida de la válvula aumenta monótonamente a medida que gradualmente se cierra la válvula. Y este efecto aumenta la pendiente de la curva del sistema, llegando a un valor de infinito cuando la válvula está completamente cerrada.
El comportamiento descrito anteriormente se contrasta con la curva de rendimiento del ventilador centrífugo que impulsa el flujo. Comparando el flujo medido directamente con la tasa de flujo calculó por la intersección de la curva del sistema y la curva de desempeño del ventilador, se demostró que este punto de intersección define las condiciones de la demanda de tasa y presión de flujo.
Este experimento sirvió el propósito de demostrar los principios de conservación de energía para caracterizar unas diferentes aplicaciones de ingeniería: válvula de operación, medición del caudal y condiciones de un sistema de flujo de trabajo. Conservación de la energía puede ser utilizada básicamente para caracterizar cualquier sistema de flujo, estos son dos ejemplos más de las aplicaciones de la ecuación de energía:
La energía cinética por el viento pueden ser cosechada por las turbinas de viento para producir energía eléctrica. Comparando aguas arriba con condiciones de flujo aguas abajo, la ecuación de energía puede utilizarse para determinar cuánta energía se ha eliminado del viento. La magnitud de la energía recuperada se dará por el trabajo de eje, , en la ecuación (1).
, en la ecuación (1).
El cambio en energía potencial gravitatoria puede utilizarse para evaluar la tasa de flujo de agua sobre un vertedero. Esto se hace en combinación con la ecuación conservación de masa midiendo las profundidades aguas arriba y aguas abajo del aliviadero. Para flujo turbulento, la ecuación sería una buena aproximación de la tasa de flujo sobre el vertedero:
 (11)
(11)
Aquí,  es el ancho del canal y
es el ancho del canal y  y
y  son las profundidades aguas arriba y aguas abajo respectivamente.
son las profundidades aguas arriba y aguas abajo respectivamente.
Referencias
- White, F. M. Fluid Mechanics, 7th ed., McGraw-Hill, 2009.
- Munson, B.R., D.F. Young, T.H. Okiishi. Fundamentals of Fluid Mechanics. 5th ed., Wiley, 2006.
Tags
Saltar a...
Vídeos de esta colección:

Now Playing
Enfoque de conservación de la energía para el análisis de sistemas
Mechanical Engineering
7.4K Vistas

Flotabilidad y arrastre en cuerpos sumergidos
Mechanical Engineering
29.9K Vistas

Estabilidad de los buques flotantes
Mechanical Engineering
22.4K Vistas

Propulsión y empuje
Mechanical Engineering
21.6K Vistas

Redes de tuberías y pérdidas de presión
Mechanical Engineering
58.0K Vistas

Enfriamiento y ebullición
Mechanical Engineering
7.7K Vistas

Saltos hidráulicos
Mechanical Engineering
40.9K Vistas

Análisis del intercambiador de calor
Mechanical Engineering
28.0K Vistas

Introducción a la refrigeración
Mechanical Engineering
24.6K Vistas

Anemometría de hilo caliente
Mechanical Engineering
15.5K Vistas

Medición de flujos turbulentos
Mechanical Engineering
13.5K Vistas

Visualización de flujo más allá de un cuerpo no fuselado
Mechanical Engineering
11.8K Vistas

Jet que inciden sobre una placa inclinada
Mechanical Engineering
10.7K Vistas

Conservación de masa y mediciones de tasa de flujo
Mechanical Engineering
22.6K Vistas

Determinación de las fuerzas de impacto en una placa plana con el método del control del volumen
Mechanical Engineering
26.0K Vistas
ACERCA DE JoVE
Copyright © 2025 MyJoVE Corporation. Todos los derechos reservados