Pandeo de columnas de acero

Fuente: Roberto León, Departamento de Ingeniería Civil y ambiental, Virginia Tech, Blacksburg, VA

En el diseño de obras civiles, es importante proporcionar estructuras que no son sólo seguros bajo cargas inesperadas, pero también proporcionan funcionamiento excelente bajo cargas todos los días a un costo económico razonable. El último está a menudo vinculado con mínimo uso de materiales, facilidad de fabricación y la rápida construcción en el campo. Las estructuras hechas de acero de los miembros pueden ser muy económicos debido a la gran resistencia del material y la prefabricación amplia de sus miembros y las conexiones, que ayuda a maximizar la velocidad de construcción en sitio. Generalmente, el esqueleto de una estructura de acero serán muy delgado en comparación con un hormigón armado uno. Mientras que su comportamiento en tensión se rige principalmente por la resistencia del material, el acero en compresión se rige por otro modo de falla común a todos los materiales-pandeo. Este comportamiento se demuestra fácilmente presionando hacia abajo en una regla de madera delgada, que bajo una carga de compresión repentinamente se moverá hacia un lado y perder capacidad de carga. Este fenómeno ocurrirá en cualquier miembro esbelto de una estructura. En este laboratorio, medimos la capacidad de pandeo de una serie de columnas de aluminio delgado para ilustrar este modo de falla, que con el tiempo ha dado lugar a muchos fracasos catastróficos entre ellas la del puente del río de Quebec, que se erigió en 1918.

Puesto que el fenómeno de pandeo es fácilmente observable, era bien conocido desde la antigüedad, pero analíticos penetraciones en el problema de pandeo no ganó atención hasta los años 1700 cuando los fundamentos matemáticos de la física se convirtió en un popular tema de estudio. Leonhard Euler, famoso matemático suizo, fue el primero en dar la solución a la carga de pandeo de una columna simplemente apoyada en 1742. Euler formuló su solución por el razonamiento que una columna recta perfectamente podría estar en equilibrio en dos configuraciones: una exhumó y una deformada (ligeramente flexionadas posición).

De la columna deformada, Euler postuló que el equilibrio en una configuración ligeramente doblado en el que se equilibran los momentos externos, dados la carga P actuando en una excentricidad y, por los momentos internos (M):

(EC. 1)

La cantidad y es el desplazamiento lateral a lo largo de la longitud z. El primer derivado de y es la pendiente, y la segunda derivada de y es la curvatura del miembro. La resistencia interna es proporcional a la curvatura, o hasta el momento interno dividido por la rigidez de la flexión (EI), por lo que:

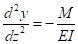(EC. 2)

En esta ecuación E es el módulo de elasticidad y es el momento de inercia, una propiedad geométrica de la sección. Ajuste y sustitución (EQ. 2) a (ecuación 1) igual a cero da la tradicional ecuación diferencial de pandeo, donde y es la deformación horizontal y k es una variable de sustitución utilizada para simplificar las ecuaciones.

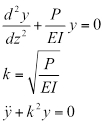(EC. 3)

Si suponemos que la deformación de la columna a lo largo de su longitud z está dada por:

(EC. 4)

y que ha fijado la columna termina, y que estos fines no desplazar lateralmente con respecto a uno otro, entonces la condición de límite en z = 0 y L, el desplazamiento lateral, es cero. Por lo tanto,

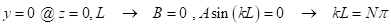(EC. 5)

donde N = 1,2,... El menor valor de N es 1, que es la carga de pandeo elástico ( _crítica P o P _cr). Para una columna con extremos fijados, (es decir, con los extremos libres girar, pero no se traducen como las condiciones de límite dadas arriba) P_cr es dada por el Euler carga de pandeo:

(EC. 6)

Es importante tener en cuenta que esta ecuación no contiene ningún término relacionado con la resistencia del material, sólo que su módulo de elasticidad (E), dimensiones y duración. El momento de inercia (I) de una sección compuesta de piezas rectangulares se da por la suma sobre el centroide de la sección de dos componentes: el momento de inercia de cada rectángulo (bd³12) más su área (A) veces su distancia desde el centroide de toda la sección (d):

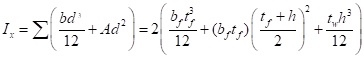(EQ. 7)

EQ 7 destaca que el valor de I puede incrementarse significativamente poniendo la mayor parte del material lo más lejos del centroide como sea posible (es decir, mediante la optimización de d). Por ejemplo, para un área total fija de 13 pulgadas², uno podría optar por dos distribuciones: un único rectángulo de 13 pulg x 1 pulg., resultando en un total de 183 pulg⁴o (b) una sección en forma de W con dos bridas de 6,5 pulg. x 0,45 pulg conectado con una red de 0,35 pulg. x 19,1 pulgadas, resultando en un total de 761 pulg⁴. Claramente la forma de W será un uso más eficiente del material con respecto a la compresión, proporcionará más de 4 veces mayor capacidad pandeo. La actual forma AISC W estándar con un área de 13 pulgadas², un W21x44 (profundidad nominal de 21 pulg.) y un peso de 44 libras por pie proporciona un I de 843 pulg⁴ o 4,5 veces la de la sección rectangular.

La relación entre el momento de inercia () y área (A) se define por el radio de giro (r):

(EC. 8)

La capacidad de pandeo se expresa a veces como un esfuerzo crítico (F_cr) dividiendo la carga crítica por el área:

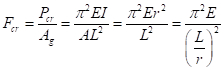(EC. 9)

Hay que tener en cuenta que existen algunas limitaciones inherentes en la derivación de la ecuación (6) y la ecuación (9) que asumen:

1. Comportamiento puramente elástico y así son válidas sólo hasta el límite proporcional del material.
2. La carga es aplicada en el centroide de la columna, que es difícil de lograr en la práctica. Por lo tanto, excentricidades iniciales accidental desempeñará un papel en el diseño.
3. La columna es inicialmente perfectamente recta. Desde formas de acero son producidos por un proceso de laminación, tienen una comba y barrido (es decir, va ser ligeramente curvadas a lo largo de ambos ejes principales). Estas imperfecciones iniciales son pequeñas, del orden de L/1000, pero hará que el comportamiento real de la columna se desvían de la de una columna idealizada.
4. Una forma desviada, que en nuestro caso tomó la forma de una función trigonométrica (es decir, una combinación de funciones seno y coseno). Para este caso, realmente utilizamos la correcta solución analítica, pero que no siempre es posible. En general, cualquier función de aproximar la solución correcta le dará un satisfactorio aproximada, pero no es una solución exacta.
5. Condiciones de extremo idealizado. Para resolver la carga de pandeo, deben establecerse las condiciones de contorno del problema matemático, y asumimos que la columna había cubrió a extremos. Además, se suponía que los extremos de la columna no se tradujo lateralmente con respecto a uno con el otro (es decir, este es el caso prevenido de balanceo, que se produce en cuadros apoyados, en comparación con el caso permitido de sacudimiento, que ocurre en marcos sin soporte). En la vida real, se pueden aproximar solamente estas condiciones idealizadas.
6. La ausencia de cualquier tensiones residuales, que surgen de la refrigeración y de las formas de acero del balanceo durante la producción. Estos resultados de tensiones en rendimiento antes de lo esperado y la pérdida de momento de inercia, como las secciones que tienen un módulo de elasticidad de cero. A medida que disminuye la rigidez de la columna, la capacidad de la columna debe disminuir, ya que la ecuación 1 tiene la IE en el numerador.

El segundo, tercero y último limitaciones generalmente se tratan juntos como imperfecciones iniciales y sus magnitudes son codificados establecido tolerancia de fabricación y construcción. Columna curvas han sido de desarrollo que aborden estas cuestiones satisfactoriamente.

Un sistema estructural/mecánico se dice que es sensible si la capacidad de carga del sistema imperfecto es sustancialmente menor que la del sistema perfecto de imperfección. Por el contrario, un sistema se dice que es imperfección insensible si no existe pérdida de la capacidad de prensores debido a las imperfecciones. Una columna se dice que es una columna perfecta si es recta y la carga es concéntrica. Mientras que esto es imposible en la práctica, somos afortunados porque columnas son insensibles de imperfección y así no tendrá ninguna pérdida súbita de capacidad de carga bajo cargas normales. Por otro lado, esferas y cilindros son sensibles de imperfección, y como resultado, mucho debe tener cuidado durante la construcción de cáscaras (cúpulas, torres de enfriamiento y tanques de almacenamiento) y otras tales estructuras para obtener la geometría correcta. El efecto de las imperfecciones es acelerar la tasa de desviación lateral, ya que tienden a aumentar los momentos de flexión en la columna.

Las limitaciones relacionadas con la quinta hipótesis, que de las condiciones de límite, pueden ser tratados simplemente por el uso del concepto de una longitud efectiva (kL). El factor de longitud efectiva k da la proporción de la longitud entre puntos de inflexión (es decir, los puntos de momento cero o cero curvatura a lo largo de la columna). Por lo tanto, la ecuación (9) puede ser reescrita como:

(EC. 10)

El denominador (kL/r) se conoce como la esbeltez de la columna. Un valor bajo (por ejemplo, kL/r < 20) es sinónimo de una columna robusta, que no es muy susceptible al pandeo, mientras que un valor grande (por ejemplo, kl/r > 100) es sinónimo de una esbelta columna, que es muy susceptible al pandeo.

Cabe señalar que el esfuerzo crítico (σ_cr) para el diseño de es Nevada por la fuerza de la producción del material (σ_y). Esta restricción significa que cualquiera dado fuerza de acero, digamos σ_y = F_y = 50 ksi _, habrá una esbeltez abajo que abrochar no ocurrirá. Si igualamos σ_cr = 50 ksi en la ecuación (10), la esbeltez límite es kl/r < 75.6.

Otra ADVERTENCIA importante es que la formulación anterior indica que de pandeo se produce repentinamente como la carga axial alcanza su valor crítico (P_cr). Matemáticamente, este hecho indica que el pandeo es un problema de bifurcación. Debido a las imperfecciones iniciales, excentricidades accidentales y tensiones residuales entre otros factores, habrá una transición entre la tensión de pandeo elástico y carga de la calabaza. El resultado de las imperfecciones iniciales es que en la vida real habrá una transición suave entre la curva de pandeo elástico y los Estados límite de rendimiento.

En este punto, es importante tener en cuenta que la inestabilidad o el fenómeno de pandeo bajo discusión es sólo uno de los muchos que pueden ocurrir. Las inestabilidades se producen tanto a nivel local y global. Inestabilidad de nivel mundial es cuando todos los elementos (un elemento se define como cualquier sección rectangular que hace de una forma) se acercan durante el pandeo. Pandeo local se produce cuando sólo uno de los elementos. Ejemplos de pandeo global son:

• Flexural de pandeo, que es el caso que se discute arriba.
• Torsional de pandeo, en que la sección gira sobre su centro longitudinal. Las secciones que tienen pequeña rigidez torsional (J) son propensas a este tipo de falla.
• Pandeo torsional lateral o torsional flexural, que es una combinación de los dos primeros tipos de pandeo global y es el modo predominante de la inestabilidad para vigas.
• Esfuerzo cortante pandeo, en el cual el pandeo ocurre en las redes finas de vigas profundas debido a la formación de un campo de tensión en la dirección diagonal.

Las secciones también pueden hebilla localmente. Esto es análogo a cada sección de la columna pandeo individualmente como un plato. Pandeo local se rige por la relación ancho a espesor (b/t) o la relación de esbeltez de la sección y relación de aspecto de la placa (b /, donde es la longitud ). La esbeltez depende de si ambos bordes de la placa están conectadas a otra sección (caso de refuerzo), o si está conectado sólo un borde (caso unstiffened). La capacidad de pandeo de una placa de ancho b y espesor t, análoga a la ecuación (10) para una columna, está dada por:

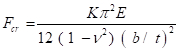(EC. 11)

El coeficiente de pandeo K refleja las condiciones de contorno y la relación de aspecto (longitud-anchura) de la placa. Valores de K están ampliamente disponibles en manuales de diseño estructural.

1. Obtener varios largos trozos de 1 pulgada por barra de aluminio de ¼ pulgadas (6061 o similar) y corte a longitud de 72, 60, 48, 36, 24, 12 y 8 pulgadas, respectivamente. Ronda ambos extremos de las barras a una circunferencia de 1/8 pulg.
2. Medir las dimensiones de la barra (longitud, anchura y grueso) a la más cercana en 0,02.
3. Máquina de dos bloque pequeño de acero (2 pulg x 2 pulg x 2 pulg.) para tener una penetración circular pulg. ½ muy suave a lo largo de uno de sus lados para servir como el soporte de extremo de la columna. Proporcionar un inserto en el lado opuesto, para que el bloque puede ser fijado a la máquina de prueba.
4. Inserte los bloques y una probeta en la máquina de prueba. Asegúrese de alinear a la muestra tan cuidadosamente como sea posible para eliminar excentricidades.
5. Prendió la máquina de prueba de control de desviación y que lentamente se aplica una deformación de 0,2 pulgadas y record carga y la deformación axial del programa. El límite puede variar con la longitud, pero la prueba debe suspenderse cuando la carga se ha estabilizado o ha llegado a no más de una reducción de la carga del 20% de la capacidad máxima.
6. La carga máxima alcanzada y rellene la tabla de resultados.
7. Repita los pasos 1.4 por 1.6 para todas las columnas.

Representar los resultados de la tabla como pandeo tensiones vs esbeltez (kL/r), junto con la curva dada por la ecuación 9. Comparar sus resultados con los valores predichos. Los resultados experimentales muestra dos regiones distintas. Cuando las columnas son relativamente largas, la carga crítica viene dada por multiplicar la EC. 9 por la zona de la columna. Como las columnas comienzan a conseguir más cortos, la carga crítica comienza a acercarse a la resistencia del material. En este punto el comportamiento cambia de uno puramente elástico a una parcial inelástica que se acerca asintóticamente a la carga de la calabaza de la columna. Cuando una columna hebillas elástico, la deformación puede convertirse en cada grande de pronto y provocar fallas en el miembro abrochado o en los adyacentes que sobrecargarse como el miembro abrochado arroja sus cargas. Así, en el diseño es importante evitar fallos de pandeo elástico en miembros estructurales primarios.

Este experimento demostró la validez de la aproximación de Euler para calcular cargas para columnas simples de pandeo local. Aunque el problema se vuelve mucho más complicado si las condiciones de contorno no son bien conocidas, los miembros no prismáticos, o si el material no exhibe una curva bi-linear de la tensión, la solución del problema sigue el mismo proceso general. En muchos casos prácticos, no será posible resolver las ecuaciones diferenciales resultantes exactamente, pero son muchas las técnicas numéricas que pueden ser aplicadas para aproximar la solución a esos problemas. Se reconoce la importancia de pandeo en el aforismo de la industria de la construcción que sostiene que el éxito del diseño de estructuras de acero se basa en una comprensión buena de pandeo cuestiones, mientras que el éxito del diseño de estructuras de hormigón armado se basa en buena detalle.

Economía en el diseño requiere que se minimice el volumen de material. Este detalle es particularmente cierto para la construcción de metal y estructuras de puente, donde los costos de materiales son una parte importante de los costes estructurales. En general, minimizar el costo se reduce a conseguir la menor L /r. A L fijo, esto significa obtener el más grande posible r (o más grande que para un dado), líder en el uso generalizado de los miembros en forma de W. Para un fijo r, esto significa disminución de L, que consiste en el uso de miembros de arriostramiento. Para una forma de W, allí será tanto un I_x y_yy correspondiente (kL/r)_x y (kL/r)_y; para el diseño óptimo, ambos de estos valores deben estar cerca unas de otras, que a menudo se obtiene al proporcionar más refuerzo en la dirección y. Otra manera de prevenir el pandeo es agregar refuerzos, que reducen las longitudes de pandeo de placas; ejemplos de estos incluyen refuerzos en vigas de placa puente y labios de rigidez en los miembros estructurales de forma fría.