Instabilità delle colonne d'acciaio

Fonte: Roberto Leon, Dipartimento di Ingegneria Civile e Ambientale, Virginia Tech, Blacksburg, VA

Nella progettazione di opere civili, è importante fornire strutture che non solo siano sicure sotto carichi imprevisti, ma forniscano anche prestazioni eccellenti sotto carichi quotidiani a un costo economico ragionevole. Quest'ultimo è spesso legato all'uso minimo di materiali, alla facilità di fabbricazione e alla rapida costruzione sul campo. Le strutture realizzate con membri in acciaio possono essere molto economiche a causa della grande resistenza del materiale e dell'ampia prefabbricazione dei loro membri e connessioni, che aiutano a massimizzare la velocità di costruzione in loco. Generalmente, lo scheletro di una struttura in acciaio sarà molto snello rispetto a uno in cemento armato. Mentre il suo comportamento in tensione è governato principalmente dalla resistenza del materiale, l'acciaio in compressione è governato da un'altra modalità di guasto comune a tutti i materiali: la deformazione. Questo comportamento è facilmente dimostrabile premendo verso il basso su un righello di legno sottile, che sotto un carico di compressione si sposterà improvvisamente lateralmente e perderà capacità di carico. Questo fenomeno si verificherà in qualsiasi membro snello di una struttura. In questo laboratorio, misureremo la capacità di instabilità di una serie di esili colonne in alluminio per illustrare questa modalità di guasto, che nel tempo ha portato a molti guasti catastrofici tra cui quello del Quebec River Bridge, che è stato eretto nel 1918.

Poiché il fenomeno della deformazione è facilmente osservabile, era ben noto fin dall'antichità, ma le intuizioni analitiche sul problema della deformazione non hanno attirato l'attenzione fino al 1700, quando le basi matematiche della fisica sono diventate un popolare argomento di studio. Leonhard Euler, un famoso matematico svizzero, fu il primo a fornire la soluzione al carico di instabilità di una colonna semplicemente sostenuta nel 1742. Eulero formulò la sua soluzione ragionando che una colonna perfettamente diritta poteva essere in equilibrio in due configurazioni: una non deformata e una deformata (posizione leggermente piegata).

Per la colonna deformata, Eulero postulò che l'equilibrio in una configurazione leggermente piegata in cui i momenti esterni, dati dal carico P che agisce ad un'eccentricità y, sono bilanciati dai momenti interni (M):

(Eq. 1)

La quantità y è lo spostamento laterale lungo la lunghezza z. La derivata prima di y è la pendenza e la derivata seconda di y è la curvatura del membro. La resistenza interna è proporzionale alla curvatura, ovvero al momento interno diviso per la rigidità di flessione (EI), in modo che:

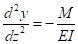(Eq. 2)

In questa equazione E è il modulo di elasticità e I è il momento di inerzia, una proprietà geometrica della sezione. Sostituendo (Eq. 2) in (Eq. 1) e impostandolo uguale a zero si ottiene l'equazione differenziale tradizionale di instabilità, dove y è la deformazione orizzontale, e k è una variabile di sostituzione usata per semplificare le equazioni.

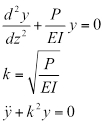(Eq. 3)

Se assumiamo che la deformazione della colonna lungo la sua lunghezza z sia data da:

(Eq. 4)

e che la colonna ha estremità bloccate e che queste estremità non si spostano lateralmente l'una rispetto all'altra, quindi la condizione al contorno a z = 0 e L, lo spostamento laterale, è zero. Così

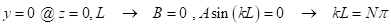(Eq. 5)

dove N= 1,2, .... Il valore più basso per N è 1, che è il carico di deformazione elastico (P _critico o P _cr). Per una colonna con estremità bloccate, (cioè con estremità libere di ruotare, ma non di traslarsi come le condizioni al contorno sopra indicate) P_cr è dato dal carico di deformazione di Eulero:

(Eq. 6)

È importante notare che questa equazione non contiene termini relativi alla resistenza del materiale, ma solo al suo modulo di elasticità (E), dimensioni e lunghezza. Il momento di inerzia (I) di una sezione costituita da parti rettangolari è dato dalla sommatoria intorno al centroide della sezione di due componenti: il momento di inerzia del singolo rettangolo (bd³/12) più la sua area (A) volte la sua distanza dal centroide dell'intera sezione (d):

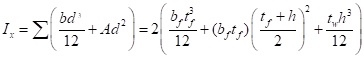(Eq. 7)

Eq. 7 evidenzia che il valore di I può essere aumentato in modo significativo mettendo la maggior parte del materiale il più lontano possibile dal centroide (cioè massimizzando d). Ad esempio, per un'area totale fissa di 13 in.², si potrebbe optare per due distribuzioni: (a) un singolo rettangolo di 13 in. x 1 in., risultante in un totale I di 183 in.⁴, o (b) una sezione a forma di W con due flange di 6,5 in. x 0,45 in. collegato con un nastro di 0,35 in. x 19,1 in., risultando in un totale I di 761 in.⁴. Chiaramente la forma a W sarà un uso molto più efficiente del materiale rispetto alla compressione, in quanto fornirà una capacità di deformazione oltre 4 volte maggiore. L'attuale forma a W AISC standard con un'area di 13 in.², un W21x44 (profondità nominale di 21 pollici e un peso di 44 libbre per piede) fornisce un I di 843 in.⁴ o oltre 4,5 volte quello della sezione rettangolare.

La relazione tra il momento di inerzia (I) e l'area (A) è definita dal raggio di rotazione (r):

(Eq. 8)

La capacità di instabilità è talvolta espressa come sollecitazione critica (F_cr)dividendo il carico critico per l'area:

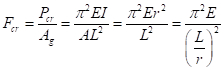(Eq. 9)

Bisogna tenere presente che ci sono alcune limitazioni inerenti alla derivazione di Eq. (6) e Eq. (9) in quanto assumono:

1. Comportamento puramente elastico, e quindi sono validi solo fino al limite proporzionale del materiale.
2. Il carico viene applicato al centroide della colonna, che è difficile da ottenere nella pratica. Pertanto, le eccentricità iniziali accidentali avranno un ruolo nel design.
3. La colonna è inizialmente perfettamente dritta. Poiché le forme di acciaio sono prodotte da un processo di laminazione, avranno una campanatura e una spazzata (cioè, saranno leggermente curve lungo entrambi gli assi principali). Queste imperfezioni iniziali sono piccole, dell'ordine di L/1000, ma faranno deviare il comportamento reale della colonna da quello di una colonna idealizzata.
4. Una forma deviata, che nel nostro caso ha assunto la forma di una funzione trigonometrica (cioè una combinazione di funzioni seno e coseno). Per questo caso, abbiamo effettivamente utilizzato la soluzione analitica corretta, ma ciò non è sempre possibile. In generale, qualsiasi funzione che si avvicini alla soluzione corretta darà una soluzione approssimativa soddisfacente, ma non esatta.
5. Condizioni finali idealizzate. Per risolvere il carico di instabilità, è necessario stabilire le condizioni al contorno del problema matematico e abbiamo ipotizzato che la colonna avesse estremità bloccate. Inoltre, si presumeva che le estremità della colonna non si traducessero lateralmente l'una rispetto all'altra (cioè, questo è il caso impedito dall'oscillazione, che si verifica nei fotogrammi rinforzati, al contrario del caso consentito dall'oscillazione, che si verifica nei fotogrammi non bracci). Nella vita reale, queste condizioni idealizzate possono essere solo approssimate.
6. L'assenza di tensioni residue, che derivano dal raffreddamento e dalla laminazione delle forme dell'acciaio durante la produzione. Queste sollecitazioni provocano una resa prima del previsto e la perdita di momento di inerzia, poiché le sezioni che cedono hanno un modulo di elasticità pari a zero. Man mano che la rigidità della colonna diminuisce, la capacità della colonna deve diminuire, poiché Eq. 1 ha EI nel numeratore.

La seconda, la terza e l'ultima limitazione sono generalmente trattate insieme come imperfezioni iniziali e le loro grandezze sono fondamentali per stabilire la tolleranza di costruzione e fabbricazione. Sono state sviluppate curve di progettazione delle colonne che affrontano questi problemi in modo soddisfacente.

Un sistema strutturale/meccanico è detto sensibile all'imperfezione se la capacità di carico del sistema imperfetto è sostanzialmente inferiore a quella del sistema perfetto. Al contrario, un sistema è detto insensibile all'imperfezione se non vi è alcuna perdita di capacità di carico a causa delle imperfezioni. Si dice che una colonna è una colonna perfetta se è diritta e il carico è concentrico. Mentre questo è impossibile nella pratica, siamo fortunati perché le colonne sono insensibili all'imperfezione e quindi non avranno alcuna improvvisa perdita di capacità di carico sotto carichi normali. D'altra parte, sfere e cilindri sono sensibili all'imperfezione e, di conseguenza, è necessario prestare molta attenzione durante la costruzione di gusci (cupole, torri di raffreddamento e serbatoi di stoccaggio) e altre strutture simili per ottenere la geometria corretta. L'effetto delle imperfezioni è quello di accelerare la velocità di deflessione laterale, poiché tendono ad aumentare i momenti di flessione nella colonna.

Le limitazioni relative alla quinta ipotesi, quella delle condizioni al contorno, possono essere trattate semplicemente con l'uso del concetto di lunghezza effettiva (kL). Il fattore di lunghezza effettivo k fornisce la proporzione della lunghezza tra i punti di inflessione (cioè punti di momento zero o curvatura zero lungo la colonna). Pertanto, Eq. (9) può essere riscritto come:

(Eq. 10)

Il denominatore (kL/r) è noto come snellezza della colonna. Un valore basso (ad esempio, kL/r < 20) è sinonimo di una colonna tozza, che non è molto suscettibile alla deformazione, mentre un grande valore (ad esempio, kl/r > 100) è sinonimo di una colonna snella, che è molto suscettibile alla deformazione.

Va notato che la sollecitazione critica (σ_cr) per la progettazione è limitata dal limite di snervamento del materiale (σ_y). Questo vincolo significa che per ogni data resistenza dell'acciaio, diciamo σ_y = F_y = 50 ksi _, ci sarà una snellezza al di sotto della quale non si verificherà la deformazione. Se equipariamo σ_cr = 50 ksi in Eq. (10), il limite di snellezza è kl/r < 75,6.

Un altro avvertimento importante è che la formulazione di cui sopra indica che la deformazione si verificherà improvvisamente quando il carico assiale raggiunge il suo valore critico (P_cr). Matematicamente, questo fatto indica che la deformazione è un problema di biforcazione. A causa di imperfezioni iniziali, eccentricità accidentali e tensioni residue tra gli altri fattori, ci sarà una transizione tra lo stress di deformazione elastica e il carico di schiacciamento. Il risultato di queste imperfezioni iniziali è che nella vita reale ci sarà una transizione graduale tra la curva di deformazione elastica e gli stati limite di rendimento.

A questo punto, è importante notare che il fenomeno dell'instabilità o della deformazione in discussione è solo uno dei tanti che possono verificarsi. Le instabilità si verificano sia a livello locale che globale. L'instabilità a livello globale si presenta quando tutti gli elementi (un elemento è definito come qualsiasi sezione rettangolare che costituisce una forma) si muovono insieme durante la deformazione. La deformazione locale si verifica quando solo uno degli elementi si muove. Esempi di instabilità globale sono:

• Instabilità flessionale, che è il caso discusso sopra.
• Instabilità torsionale, in cui la sezione ruota intorno al suo centroide longitudinale. Le sezioni che hanno una piccola rigidità torsionale (J) sono soggette a questo tipo di guasto.
• Flessione-torsionale o laterale-torsionale, che è una combinazione dei primi due tipi di deformazione globale ed è la modalità di instabilità predominante per le travi.
• Deformazione a taglio, in cui la deformazione si verifica nelle sottili reti di travi profonde a causa della formazione di un campo di tensione nella direzione diagonale.

Le sezioni possono anche allacciarsi localmente. Questo è analogo a ciascuna sezione della colonna che si piega individualmente come una piastra. La deformazione locale è regolata dal rapporto larghezza-spessore (b/t) o dal rapporto di snellezza della sezione e dal rapporto di aspetto della piastra (b/a, dove a è la lunghezza). La snellezza dipende dal fatto che entrambi i bordi della piastra siano collegati a un'altra sezione (custodia irrigidita) o che sia collegato un solo bordo (caso non offeso). La capacità di deformazione di una lastra di larghezza b e spessore t,analoga a Eq. (10) per una colonna, è data da:

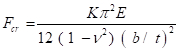(Eq. 11)

Il coefficiente di deformazione K riflette le condizioni al contorno e le proporzioni (lunghezza-larghezza) della piastra. I valori di K sono ampiamente disponibili nei manuali di progettazione strutturale.

1. Ottenere diversi pezzi lunghi di una barra di alluminio da 1 pollici per 1/4 di in . (6061 o simile) e tagliarli a lunghezze di 72, 60, 48, 36, 24, 12 e 8 pollici, rispettivamente. Arrotondare entrambe le estremità delle barre fino a una circonferenza di 1/8 di in.
2. Misurare le dimensioni della barra (lunghezza, larghezza e spessore) con l'stanza più vicina di 0,02 pollici.
3. Lavorare due piccoli blocchi di acciaio (2 pollici x 2 pollici x 2 pollici) per avere una penetrazione circolare molto liscia di 1/2 pollici lungo uno dei suoi lati per fungere da supporto per l'estremità della colonna. Fornire un inserto sul lato opposto, in modo che il blocco possa essere fissato alla macchina di prova.
4. Inserire i blocchi e un campione di prova nella macchina di prova. Assicurarsi di allineare il campione il più attentamente possibile per eliminare le eccentricità.
5. Impostare la macchina di prova sul controllo della deflessione e programmarla per applicare lentamente una deformazione fino a 0,2 pollici e registrare il carico e la deformazione assiale. Il limite può essere variato con la lunghezza, ma la prova deve essere interrotta quando il carico si è stabilizzato o quando ha raggiunto una riduzione del carico non superiore al 20% rispetto alla capacità massima.
6. Registrare il carico massimo raggiunto e compilare la tabella dei risultati.
7. Ripetere i passaggi da 1.4 a 1.6 per tutte le colonne.

Traccia i risultati della tabella come sollecitazioni di deformazione rispetto alla snellezza (kL / r), insieme alla curva data da Eq. 9. Confronta i risultati con i valori previsti. I risultati sperimentali mostrano due regioni distinte. Quando le colonne sono relativamente lunghe, il carico critico è dato moltiplicando Eq. 9 per l'area della colonna. Quando le colonne iniziano ad accorciarsi, il carico critico inizia ad avvicinarsi alla forza del materiale. A questo punto il comportamento si sposta da uno puramente elastico ad uno parzialmente anelastico che si avvicina asintoticamente al carico di squash della colonna. Quando una colonna si piega elasticamente, la deformazione può diventare improvvisamente grande e innescare guasti sia nell'elemento piegato che in quelli adiacenti che si sovraccaricano man mano che l'elemento allacciato perde i suoi carichi. Pertanto, nella progettazione è importante prevenire i cedimenti di deformazione elastica negli elementi strutturali primari.

Questo esperimento ha dimostrato la validità dell'approccio di Eulero per il calcolo dei carichi di instabilità locali per colonne semplici. Sebbene il problema diventi molto più complicato se le condizioni al contorno non sono ben note, il membro non è prismatico, o se il materiale non presenta una curva tra sollecitazione e deformazione bi-lineare, la soluzione del problema segue lo stesso processo generale. In molti casi pratici, non sarà possibile risolvere esattamente le equazioni differenziali risultanti, ma ci sono molte tecniche numeriche che possono essere applicate per approssimare la soluzione a quei problemi. L'importanza della deformazione è riconosciuta nell'aforisma del settore delle costruzioni che sostiene che la progettazione di successo di strutture in acciaio si basa su una buona comprensione dei problemi di instabilità, mentre la progettazione di successo di strutture in cemento armato si basa su buoni dettagli.

L'economia nella progettazione richiede che il volume del materiale sia ridotto al minimo. Questo dettaglio è particolarmente vero per le costruzioni metalliche e le strutture a ponte, dove i costi dei materiali sono una parte significativa del costo strutturale totale. In generale, ridurre al minimo i costi si riduce a ottenere il più basso L /r. Per una L fissa, questo significa ottenere la più grande r possibile (o la più grande I per un dato A), portando all'uso diffuso di membri a forma di W. Per un rfisso , questo significa diminuire L, che comporta l'uso di membri di rinforzo. Per una forma a W, ci saranno sia un I_x che I_y, e corrispondenti (kL / r)_x e (kL / r)_y; per una progettazione ottimale, entrambi questi valori dovrebbero essere vicini l'uno all'altro, che spesso si ottiene fornendo più rinforzo nella direzione y. Un altro modo per prevenire la deformazione è aggiungere irrigidimenti, che riducono le lunghezze di deformazione nelle piastre; esempi di questi includono irrigidimenti nelle travi delle piastre del ponte e labbra di irrigidimento negli elementi strutturali a forma fredda.