Knicken von Stahlstützen

Quelle: Roberto Leon, Department of Civil and Environmental Engineering, Virginia Tech, Blacksburg, VA

In der Ausführung von Bauarbeiten ist es wichtig, Strukturen, die sind nicht nur sicher bei unerwarteten Belastungen, sondern auch hervorragende Leistung unter alltäglichen Belastungen zu einem vernünftigen wirtschaftlichen Preis zu liefern. Letzteres ist oft auf minimaler Einsatz von Materialien, einfache Fertigung und schnelle Konstruktion im Bereich gebunden. Strukturen aus Stahl gefertigt, die Mitglieder sehr sparsam wegen die große Stärke des Materials und der umfangreichen Vorfertigung ihrer Mitglieder und Verbindungen, die dazu beitragen werden können, die Geschwindigkeit des Aufbaus vor Ort zu maximieren. Im Allgemeinen wird das Skelett einer Stahlstruktur sehr schlank im Vergleich zu einer Stahlbeton eine sein. Während seines Verhaltens in Spannung vor allem durch die Stärke des Materials geregelt ist, unterliegt ein weiteres Ausfallmodus üblich, alle Materialien-Knick Stahl in der Kompression. Dieses Verhalten wird einfach durch Drücken auf eine schlanke Holzlineal veranschaulicht, die unter einer Druckbelastung plötzlich seitwärts bewegen und Tragfähigkeit zu verlieren. Dieses Phänomen tritt in einer schlanken Member einer Struktur. In dieser Übungseinheit messen wir die Knick Kapazität einer Reihe von schlanken Aluminium-Säulen zu diesem Ausfallmodus zu illustrieren, die im Laufe der Zeit zu viele katastrophale Ausfälle, einschließlich derjenigen der Quebec River Bridge, im Jahre 1918 errichtete geführt hat.

Da das Phänomen der Knickung leicht beobachtbar ist, hat es war seit der Antike bekannt, aber analytische Einblicke in das Problem der Knickung nicht Aufmerksamkeit bis 1700 als die mathematischen Grundlagen der Physik ein populäres Thema der Studie wurde. Leonhard Euler, einem berühmten Schweizer Mathematiker, war der erste, der die Lösung für die Knicklast einer einfach unterstützten Spalte 1742 liefern. Euler formuliert seine Lösung durch eine Begründung, die eine schnurgeraden Spalte im Gleichgewicht in zwei Konfigurationen werden könnte: eine unverformten und einem deformierten (leicht gebeugten Position).

Für die deformierte Spalte Euler postuliert, dass das Gleichgewicht in einer leicht angewinkelten Konfiguration, in denen die externe Momente, gegeben durch die Last P Schauspiel an einer Exzentrizität y, durch die interne Momente (M ausgewogen sind):

(GL. 1)

Die Menge y ist die seitliche Verschiebung entlang der Länge Z. Die erste Ableitung von y ist die Steigung, und die zweite Ableitung von y ist die Krümmung des Mitglieds. Der Innenwiderstand ist proportional der Krümmung oder dem internen Moment dividiert durch die Biegesteifigkeit (EI), so dass:

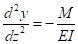(GL. 2)

In dieser Gleichung ist E der Elastizitätsmodul und ich ist das Trägheitsmoment, eine geometrische Eigenschaft des Abschnitts. Substitution (GL. 2) in (GL. 1) und Einstellung es gleich NULL gibt die traditionelle Differentialgleichung der Knickung, wo y ist die horizontale Verformung, und k ist eine Substitution-Variable verwendet, um die Gleichungen zu vereinfachen.

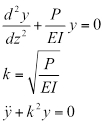(GL. 3)

Wenn wir davon ausgehen, dass die Spalte Verformung entlang seiner Länge Z von gegeben ist:

(GL. 4)

und endet, dass die Spalte fixiert hat und diese enden nicht seitlich in Bezug auf einander, dann die Randbedingung zu verdrängen Z = 0 und L, die seitliche Verschiebung ist gleich NULL. So,

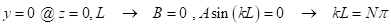(GL. 5)

wo N = 1,2,... Der niedrigste Wert für N ist 1, die die elastischen Knicklast (P _kritische oder P _Cr) ist. Für eine Spalte mit fixierten enden (d. h. mit Enden frei drehen, aber nicht zu übersetzen, als die oben angegebenen Randbedingungen) P_Cr ist gegeben durch die Euler Knicken Last:

(GL. 6)

Es ist wichtig zu beachten, dass diese Gleichung keine Begriffe im Zusammenhang mit der Festigkeit des Materials, nur für seine e-Modul von Elastizität (E), Dimensionen und Länge enthält. Das Trägheitsmoment (I) eines Abschnitts besteht aus rechteckigen Teilen ergibt sich aus der Summierung über dem Schwerpunkt des Abschnitts aus zwei Komponenten: Das Trägheitsmoment des einzelnen Rechtecks (bd³12) plus die Fläche (A) Mal seine Entfernung von der Schwerpunkt des gesamten Abschnitts (d):

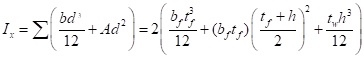(GL. 7)

EQ. 7 hebt hervor, dass der Wert von I deutlich erhöht werden kann, indem man ein Großteil des Materials möglichst weit entfernt von dem Schwerpunkt wie möglich (d. h. durch die Maximierung d). Beispielsweise für eine feste Fläche von 13 Zoll², man konnte entscheiden Sie sich für zwei Verteilungen: (a) eine einzelne Rechteck von 13 Zoll x 1 Zoll, was ich von 183 Zoll⁴oder (b) eine W-förmige Abschnitt mit zwei Flanschen von 6,5 Zoll x 0,45 Zoll mit einem Netz von verbunden insgesamt 0,35 Zoll x 19,1 Zoll, wodurch insgesamt ich 761 Zoll⁴. Deutlich werden die W-Form eine viel effizientere Nutzung des Materials in Bezug auf die Kompression, da es über 4-mal größere Knick Kapazität bereitstellen wird. Der tatsächliche standard AISC W-Form mit einer Fläche von 13 Zoll², ein W21x44 (geringe Tiefe von 21 Zoll) und einem Gewicht von 44 lbs pro Fuß bietet ein I 843 Zoll⁴ oder 4,5-Mal, von rechteckigem Querschnitt.

Die Beziehung zwischen dem Trägheitsmoment (ich) und Fläche (A) wird durch den Radius der Drehung (R) definiert:

(GL. 8)

Der Knick Kapazität wird manchmal als eine kritische Belastung (F_Cr) ausgedrückt, durch Division der kritischen Belastung durch die Gegend:

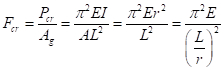(GL. 9)

Man muss daran denken, dass es einige Einschränkungen innewohnt, die Ableitung von GL. (6) und GL. (9 gibt), dass sie davon ausgehen:

1. Rein elastische Verhalten, und damit sie gelten nur bis zur proportionalen Begrenzung des Materials.
2. Die Last ist auf den Schwerpunkt der Spalte, die schwer zu erreichen in der Praxis angewendet. So werden zufällige erste Exzentrizitäten im Design eine Rolle spielen.
3. Die Spalte ist zunächst vollkommen gerade. Weil die Stahlprofile durch ein Walzverfahren hergestellt werden, haben sie eine Wölbung und Sweep (d. h. sie werden leicht gebogen werden entlang der beiden Hauptachsen). Diese anfängliche Mängel sind klein, in der Größenordnung von L/1000, aber reale Spalte Verhalten abweichen von derjenigen einer idealisierten Spalte bilden.
4. Ein abgefälschter Form, die in unserem Fall die Form einer trigonometrische Funktion (d. h. eine Kombination von Sinus und Kosinus Funktionen) annahm. In diesem Fall wir tatsächlich die richtige analytische Lösung verwendet, aber das ist nicht immer möglich. Im Allgemeinen wird jede Funktion die richtige Lösung Annäherung eine zufrieden stellende geben ungefähre, aber keine exakte Lösung.
5. Idealisierte Endbedingungen. Um für die Knicklast zu lösen, müssen die Randbedingungen für das mathematische Problem geschaffen werden, und wir davon ausgegangen, dass die Spalte enden fixiert hatte. Darüber hinaus wurde davon ausgegangen, dass die Enden der Spalte nicht seitlich zueinander übersetzen (d.h., dies gilt Sway verhindert, die in Versteifter Rahmen, im Gegensatz zu der Herrschaft erlaubt Fall Auftritt bei Unverspannte Frames). Im wirklichen Leben können diese idealisierten Bedingungen nur angenähert werden.
6. Das Fehlen jeder Eigenspannungen, die aus der Kühlung und Rollen der Stahlprofile während der Produktion entstehen. Diese betont Ergebnisse in ertragreiche früher als erwartet und der Verlust des Trägheitsmoments, wie in den Abschnitten nachgeben haben einen Elastizitätsmodul von NULL. Wenn die Spalte Steifigkeit abnimmt, hat eine Kapazität von der Spalte zu verringern, da GL. 1 EI im Zähler hat.

Die zweite, dritte und letzte Einschränkungen sind in der Regel als anfängliche Mängel zusammen behandelt, und ihre Größen eingegeben werden, um bewährte Konstruktion und Fertigung Toleranz. Säulen-Konstruktion, die Kurven wurden entwickelt diese Adresse diese Fragen zufriedenstellend.

Ein Struktur-/mechanische System soll Unvollkommenheit empfindlich wenn die Tragfähigkeit des unvollkommenen Systems wesentlich geringer als das perfekte System ist. Im Gegensatz dazu soll ein System sein Unvollkommenheit unempfindlich ist kein Kapazitätsverlust Loadcarrying wegen der Mängel. Eine Spalte soll eine perfekte Spalte sein, wenn es gerade, und die Last konzentrisch ist. Während dies in der Praxis unmöglich ist, sind wir glücklich, weil Spalten Unvollkommenheit unempfindlich sind, und somit keinen plötzlichen Verlust der Tragfähigkeit unter normaler Belastung. Auf der anderen Seite, Kugeln und Zylinder sind sensible Unvollkommenheit, und infolgedessen viel Sorgfalt angegeben werden während der Bauphase von Muscheln (Kuppeln, Kühltürme, und Lagertanks) und andere solche Strukturen, die richtige Geometrie zu erhalten. Die Unvollkommenheiten bewirkt, die Rate der seitlichen Auslenkung zu beschleunigen, da sie dazu neigen, die Biegemomente in der Spalte zu erhöhen.

Die Beschränkungen in Bezug auf die fünfte Annahme, die der Randbedingungen, einfach durch die Verwendung des Begriffs der eine Nutzlänge (kL) behandelt werden können. Die Nutzlänge Faktor k gibt den Anteil der Länge zwischen Beugungspunkte (d. h. Punkte NULL Moment oder Null Krümmung entlang der Spalte). GL. (9) kann daher als umgeschrieben werden:

(GL. 10)

Der Nenner (kL/R) ist bekannt als die Schlankheit der Spalte. Ein niedriger Wert (z. B. kL/R < 20) ist Synonym für eine stämmige Spalte, die nicht sehr anfällig für Knicken, ist zwar ein hohen Wert (z. B. kl/R > 100) Synonym für eine schlanke Säule, die sehr für Knicken anfällig.

Es sei darauf hingewiesen, dass der kritischen Spannung (σ_Cr) für Design durch die Streckgrenze des Materials (σ_y) begrenzt ist. Diese Einschränkung bedeutet, dass für jeden Stahl Stärke, sagen σ_y = F_y = 50 Ksi _, werden unten eine Schlankheit welche Knicken wird nicht auftreten. Wenn wir σ_{Cr gleichsetzen} = 50 Ksi in GL. (10), ist die Grenze Schlankheit kl/R < 75,6.

Eine weitere wichtige Einschränkung ist, dass die oben genannten Formulierung zeigt, dass Knicken plötzlich auftreten wird, da die axiale Belastung ihren kritischen Wert (P_Cr) erreicht. Mathematisch, zeigt diese Tatsache, dass Beulen eine Bifurkation Problem. Wegen der anfänglichen Mängel, versehentliche Exzentrizitäten und Eigenspannungen unter anderem ein Übergang zwischen den elastischen Knickung Stress und laden Sie die Squash. Diese anfängliche Mängel führt dazu, dass im wirklichen Leben ein reibungslosen Übergang zwischen der elastischen Knick-Kurve und die Ausbeute Grenzzuständen werden wird.

An dieser Stelle ist es wichtig zu beachten, dass die Instabilität oder Knick Phänomen in der Diskussion ist nur einer von vielen, die auftreten können. Instabilitäten auftreten, sowohl auf lokaler und globaler Ebene. Globaler Ebene Instabilität ist, wenn alle Elemente (ein Element ist definiert als jede rechteckigem Querschnitt, aus denen sich eine Form) während der Knickung zusammenrücken. Lokalen Knicken tritt auf, wenn nur eines der Elemente bewegt. Beispiele für globales ausknicken sind:

• Biege-und Beulen, die der Fall oben besprochen ist.
• Torsionssteifigkeit Knicken, in dem Abschnitt über seine Längsachse Schwerpunkt dreht. Abschnitte, die kleine Torsionssteifigkeit (J) sind anfällig für diese Art von Fehler.
• Biege-Torsions oder Lateral torsional Knicken, das ist eine Kombination der ersten beiden Arten von globales ausknicken und ist der vorherrschende Instabilität-Modus für Balken.
• Scher Knicken, in dem Auftritt der Knick in die dünnen Stege des tiefen Träger aufgrund der Bildung von einem Spannungsfeld in diagonaler Richtung.

Abschnitte können auch lokal Schnalle. Dies ist analog zu jedem Abschnitt der Knickung einzeln als Platte Spalte. Lokales Beulen unterliegt das Verhältnis Breite zu Dicke (b/t) oder Schlankheit Verhältnis des Abschnitts und die Platte Seitenverhältnis (b / a, wo einem die Länge). Die Schlankheit hängt davon ab, ob beide Kanten der Platte in einen anderen Abschnitt (versteifte Gehäuse) verbunden sind, oder ob nur eine Kante verbunden ist (unversteifte Fall). Der Knick Kapazität für eine Platte von Breite b und Dicke t, analog zu GL. (10) für eine Spalte ist gegeben durch:

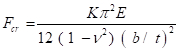(GL. 11)

Der Knick-Koeffizient K spiegelt die Randbedingungen und das Seitenverhältnis (Länge zu Breite) der Platte. Werte von K sind weit verbreitet in Tragwerksplanung Handbücher.

1. Erhalten Sie mehrere lange Stücke von einem 1 Zoll von ¼ Zoll Aluminium Bar (6061 o.ä.), und schneiden sie auf Längen von 72, 60, 48, 36, 24, 12 und 8 Zoll, beziehungsweise. Runde beide Enden der Balken, um einen Umfang von 1/8 Zoll.
2. Messen Sie die Dimensionen des Balkens (Länge, Breite und Dicke) 0,02 in am nächsten.
3. Maschine von zwei kleinen Block aus Stahl (2 Zoll x 2 Zoll x 2 Zoll), haben eine sehr glatte ½ Zoll runden Penetration entlang einer Seite als die Spalte Ende Unterstützung dienen. Geben Sie ein Insert auf der gegenüberliegenden Seite, so dass der Block an der Prüfmaschine befestigt werden kann.
4. Die Blöcke und Prüfkörper in die Prüfmaschine einfügen. Achten Sie darauf, um die Probe so schonend wie möglich zu beseitigen Exzentrizitäten auszurichten.
5. Die Prüfmaschine für Durchbiegung Steuerelement festgelegt und programmieren, langsam eine Verformung des Rekord-Last und bis zu 0,2 Zoll und axiale Verformung anzuwenden. Die Grenze mit der Länge variiert werden kann, aber der Test sollte gestoppt werden, wenn die Last stabilisiert hat oder wenn es nicht mehr als insgesamt 20 % Last aus der maximalen Kapazität erreicht hat.
6. Die maximale Belastung erreicht und füllen in der Ergebnistabelle.
7. Wiederholen Sie die Schritte 1,4 bis 1,6 für alle Spalten.

Zeichnen Sie die Ergebnisse aus der Tabelle als Knick betont vs. Schlankheit (kL/R), zusammen mit der Kurve von GL. 9 gegeben. Vergleichen Sie Ihre Ergebnisse mit den prognostizierten Werten. Die experimentellen Ergebnisse zeigt zwei verschiedene Regionen. Wenn die Spalten relativ lang sind, erhält die kritische Belastung durch Multiplikation GL. 9 durch den Bereich der Spalte. Wenn die Spalten beginnen, kürzer werden, beginnt die kritische Last nähern sich die Stärke des Materials. An dieser Stelle verschiebt sich das Verhalten von einer rein elastischen zu einer teilweisen unelastisch, die asymptotisch nähert sich die Squash-Last der Spalte. Verformung kann werden, wenn eine Spalte elastisch Schnallen, jede große plötzlich und Ausfälle in den geknickten oder im angrenzenden, die überlastet werden, da die geknickte Mitglied seine Lasten wirft auslösen. Also, im Design ist es wichtig, elastische Knick Ausfälle im primären Tragwerke zu vermeiden.

Dieses Experiment demonstriert die Gültigkeit der Euler-Ansatz für die Berechnung der lokalen Knicken Lasten für einfache Spalten. Obwohl das Problem weitaus komplizierter wird, wenn entweder die Randbedingungen nicht bekannt sind, das Mitglied ist nicht prismatische, oder wenn das Material keine Bi-linearer Spannungs-Dehnungs-Kurve aufweisen, die Lösung des Problems folgt den gleichen allgemeinen Prozess. In vielen praktischen Fällen es wird nicht möglich sein, genau die resultierende Differentialgleichungen zu lösen, aber es gibt viele numerische Methoden, die angewendet werden können, um die Lösung zu diesen Problemen anzugleichen. Knicken ist in der Bau-Industrie-Aphorismus erkannt, wie wichtig, die besagt, dass die erfolgreiche Gestaltung von Stahlkonstruktionen, auf ein gutes Verständnis ausgesagt wird der Knickung Fragen, während erfolgreiche Gestaltung von Stahlbetonkonstruktionen ist auf gute Detaillierung.

Wirtschaft im Design erfordert, dass das Volumen des Materials minimiert werden. Dieses Detail ist insbesondere für Gebäude aus Metall und Brückenkonstruktionen, wo sind die Materialkosten ein erheblicher Teil der strukturellen Gesamtkosten. Minimierung der Kosten in der Regel läuft darauf hinaus, immer die niedrigsten L /R. Für eine feste L bedeutet die größte mögliche R zu erhalten (oder größte ich für einen gegebenen A), was zu den weit verbreiteten Einsatz von W-förmige Mitglieder. Für eine feste Rbedeutet dies sinkende L, die den Gebrauch der Verstrebungen Mitglieder mit sich bringt. Bei einer W-Form, werden beide I_X und ich_y, und entsprechende (kL/R)_X und (kL/R)_y; für die optimale Auslegung sollten beide Werte nahe beieinander, die oft gewonnen wird, durch die Bereitstellung von mehr Verstrebungen in y-Richtung. Ein weiterer Weg, um Knicken ist das Hinzufügen Versteifungen, die Knicklängen in Platten zu reduzieren; Beispiele hierfür sind Versteifungen in Platte Brückenträger und Versteifung Lippen in Kälte-Form Tragwerke.