Colapso de Colunas de Aço

Fonte: Roberto Leon, Departamento de Engenharia Civil e Ambiental, Virginia Tech, Blacksburg, VA

No projeto de obras civis, é importante entregar estruturas que não só sejam seguras sob cargas inesperadas, mas também proporcionem um excelente desempenho sob cargas diárias a um custo econômico razoável. Este último é frequentemente vinculado ao uso mínimo de materiais, facilidade de fabricação e construção rápida no campo. Estruturas feitas de membros de aço podem ser muito econômicas devido à grande força do material e à extensa pré-fabricação de seus membros e conexões, que ajudam a maximizar a velocidade de construção no local. Geralmente, o esqueleto de uma estrutura de aço será muito fino em comparação com um concreto armado. Embora seu comportamento na tensão seja regido principalmente pela força do material, o aço na compressão é regido por outro modo de falha comum a todos os materiais- fivela. Este comportamento é facilmente demonstrado pressionando para baixo em uma régua de madeira esbelta, que sob uma carga compressiva de repente se moverá de lado e perderá a capacidade de carga. Este fenômeno ocorrerá em qualquer membro esguio de uma estrutura. Neste laboratório, vamos medir a capacidade de entortar de uma série de colunas de alumínio esbelto para ilustrar este modo de falha, que ao longo do tempo levou a muitas falhas catastróficas, incluindo a da Ponte do Rio Quebec, que foi erguida em 1918.

Uma vez que o fenômeno da fivela é facilmente observável, era bem conhecido desde a antiguidade, mas insights analíticos sobre o problema da fivela não ganharam atenção até 1700, quando os fundamentos matemáticos da física se tornaram um assunto popular de estudo. Leonhard Euler, um famoso matemático suíço, foi o primeiro a fornecer a solução para a carga de fivela de uma coluna simplesmente apoiada em 1742. Euler formulou sua solução argumentando que uma coluna perfeitamente reta poderia estar em equilíbrio em duas configurações: uma não deformada e uma deformada (posição ligeiramente dobrada).

Para a coluna deformada, Euler postulou que o equilíbrio em uma configuração ligeiramente dobrada em que os momentos externos, dado pela carga P agindo em uma excentricidade y, são equilibrados pelos momentos internos (M):

(Eq. 1)

A quantidade y é o deslocamento lateral ao longo do comprimento z. A primeira derivada de y é a inclinação, e a segunda derivada de y é a curvatura do membro. A resistência interna é proporcional à curvatura, ou ao momento interno dividido pela rigidez de dobra (IE), de modo que:

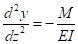(Eq. 2)

Nesta equação E está o módulo de elasticidade e eu sou o momento da inércia, uma propriedade geométrica da seção. Substituir (Eq. 2) em (Eq. 1) e defini-lo igual a zero dá a equação diferencial tradicional de fivela, onde y é a deformação horizontal, e k é uma variável de substituição usada para simplificar as equações.

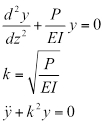(Eq. 3)

Se assumirmos que a deformação da coluna ao longo de seu comprimento z é dada por:

(Eq. 4)

e que a coluna tem extremidades fixadas, e que essas extremidades não se deslocam lateralmente em relação umas às outras, então a condição de limite em z = 0 e L, o deslocamento lateral, é zero. Assim

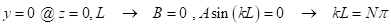(Eq. 5)

onde N= 1,2, .... O menor valor para N é 1, que é a carga de fivela elástica (P _crítico ou P _cr). Para uma coluna com extremidades fixas, (ou seja, com extremidades livres para rodar, mas não traduzidas como as condições de limite acima) P_cr é dado pela carga de fivela euler:

(Eq. 6)

É importante notar que esta equação não contém termos relacionados à força do material, apenas ao seu módulo de elasticidade (E), dimensões e comprimento. O momento da inércia (I) de uma seção composta por partes retangulares é dado pela somatória sobre o centroide da seção de dois componentes: o momento da inércia do retângulo individual (bd³/12) mais sua área (A) vezes sua distância do centroide de toda a seção (d):

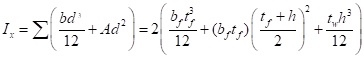(Eq. 7)

Eq. 7 destaca que o valor de I pode ser aumentado significativamente colocando a maior parte do material o mais longe possível do centroide (ou seja, maximizando d). Por exemplo, para uma área total fixa de 13 polegadas.², pode-se optar por duas distribuições: (a) um único retângulo de 13 in. x 1 in., resultando em um total I de 183 in.⁴, ou (b) uma seção em forma de W com duas flanges de 6,5 in. x 0,45 in. conectado com uma teia de 0,35 em x 19,1 em. resultando em um total de I de 761 em⁴. Claramente a forma W será um uso muito mais eficiente do material no que diz respeito à compressão, pois fornecerá mais de 4 vezes mais capacidade de fivela. A forma padrão AISC W real com uma área de 13 em^2,um W21x44 (profundidade nominal de 21 polegadas e um peso de 44 lbs. por pé) fornece um I de 843 em⁴ ou mais de 4,5 vezes o da seção retangular.

A relação entre o momento da inércia(I) e a área (A)é definida pelo raio de giro(r):

(Eq. 8)

A capacidade de fivela às vezes é expressa como um estresse crítico (F_cr) dividindo a carga crítica pela área:

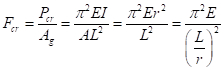(Eq. 9)

É preciso ter em mente que existem algumas limitações inerentes à derivação de Eq. (6) e Eq. (9) na qual eles assumem:

1. Comportamento puramente elástico e, portanto, são válidos apenas até o limite proporcional do material.
2. A carga é aplicada no centroid da coluna, o que é difícil de conseguir na prática. Assim, excentricidades iniciais acidentais desempenharão um papel no design.
3. A coluna é inicialmente perfeitamente reta. Uma vez que as formas de aço são produzidas por um processo de rolagem, eles terão um camber e varredura (ou seja, eles serão ligeiramente curvados ao longo de ambos os eixos principais). Essas imperfeições iniciais são pequenas, na ordem de L/1000, mas farão com que o comportamento real da coluna se desvie da de uma coluna idealizada.
4. Uma forma desviada, que no nosso caso tomou a forma de uma função trigonométrica (ou seja, uma combinação de funções seno e cossina). Para este caso, usamos a solução analítica correta, mas isso nem sempre é possível. Em geral, qualquer função que se aproxime da solução correta dará uma aproximação satisfatória, mas não uma solução exata.
5. Condições de fim idealizadas. A fim de resolver para a carga de fivela, as condições de limite para o problema matemático tem que ser estabelecida, e nós assumimos que a coluna tinha extremidades fixadas. Além disso, presumiu-se que as extremidades da coluna não se traduziam lateralmente em relação umas às outras (ou seja, este é o caso impedido de oscilação, que ocorre em quadros cintados, ao contrário do caso de oscilação permitido, que ocorre em quadros nãocidos). Na vida real, essas condições idealizadas só podem ser aproximadas.
6. A ausência de quaisquer tensões residuais, que decorrem do resfriamento e rolamento das formas de aço durante a produção. Estes estresses resultam em rendimento mais cedo do que o esperado e a perda de momento de inércia, já que as seções que rendem têm um módulo de elasticidade de zero. À medida que a rigidez da coluna diminui, a capacidade da coluna tem que diminuir, já que o Eq. 1 tem IE no numerador.

As segundas, terceiras e últimas limitações são geralmente tratadas como imperfeições iniciais, e suas magnitudes são fundamentadas para a tolerância estabelecida à construção e à fabricação. Foram desenvolvidas curvas de design de colunas que abordam essas questões de forma satisfatória.

Diz-se que um sistema estrutural/mecânico é sensível à imperfeição se a capacidade de carga do sistema imperfeito for substancialmente menor do que a do sistema perfeito. Por outro lado, diz-se que um sistema é imperfeito insensível se não houver perda da capacidade de carga por causa das imperfeições. Diz-se que uma coluna é uma coluna perfeita se for reta, e a carga é concêntrica. Embora isso seja impossível na prática, somos afortunados porque as colunas são insensíveis de imperfeição e, portanto, não terão perda súbita da capacidade de carga sob cargas normais. Por outro lado, esferas e cilindros são sensíveis à imperfeição e, como resultado, muito cuidado deve ser dado durante a construção de conchas (cúpulas, torres de resfriamento e tanques de armazenamento) e outras estruturas para obter a geometria correta. O efeito das imperfeições é acelerar a taxa de deflexão lateral, pois tendem a aumentar os momentos de dobra na coluna.

As limitações relacionadas à quinta suposição, a das condições de limite, podem ser tratadas simplesmente pelo uso do conceito de comprimento efetivo(kL). O fator de comprimento efetivo k dá a proporção do comprimento entre os pontos de inflexão (ou seja, pontos de curvatura zero ou zero ao longo da coluna). Portanto, Eq. (9) pode ser reescrito como:

(Eq. 10)

O denominador (kL/r) é conhecido como a esbelta da coluna. Um valor baixo (por exemplo, kL/r < 20) é sinônimo de uma coluna estonteante, que não é muito suscetível a fivelas, enquanto um grande valor (por exemplo, kl/r > 100) é sinônimo de uma coluna esbelta, que é muito suscetível a fivelas.

Deve-se notar que o estresse crítico (σ_cr) para o design é limitado pela força de rendimento do material (σ_y). Esta restrição significa que para qualquer força de aço, digamos σ_y = F_y = 50 ksi _, haverá uma esbelta abaixo da qual a fivela não ocorrerá. Se equipararmos σ_cr = 50 ksi em Eq. (10), o limite é kl/r < 75,6.

Outra ressalva importante é que a formulação acima indica que a fivela ocorrerá de repente à medida que a carga axial atinge seu valor crítico (P_cr). Matematicamente, este fato indica que a fivela é um problema de bifurcação. Devido às imperfeições iniciais, excentricidades acidentais e estresses residuais, entre outros fatores, haverá uma transição entre o estresse elástico e a carga de abóbora. O resultado dessas imperfeições iniciais é que na vida real haverá uma transição suave entre a curva de fivela elástica e os estados de limite de rendimento.

Neste ponto, é importante notar que a instabilidade ou o fenômeno em discussão é apenas um dos muitos que podem ocorrer. As instabilidades ocorrem tanto no nível local quanto global. Instabilidade de nível global é quando todos os elementos (um elemento é definido como qualquer seção retangular que compõe uma forma) se movem juntos durante a fivela. A dobra local ocorre quando apenas um dos elementos se move. Exemplos de fivela global são:

• A fivela flexural, que é o caso discutido acima.
• Dobra torcional, na qual a seção gira sobre seu centroide longitudinal. Seções que têm pequena rigidez torcional (J) são propensas a este tipo de falha.
• A dobra flexural-torcional ou torcional lateral, que é uma combinação dos dois primeiros tipos de fivela global e é o modo de instabilidade predominante para vigas.
• A fivela de tesoura, na qual o entortamento ocorre nas finas teias de vigas profundas devido à formação de um campo de tensão na direção diagonal.

As seções também podem ceder localmente. Isso é análogo a cada seção da coluna dobrando individualmente como uma placa. A fivela local é regida pela razão largura-espessura (b/t) ou razão de esbelta da seção e pela razão de aspecto da placa(b/a, onde a é o comprimento). A esbelta depende se ambas as bordas da placa estão conectadas a outra seção (estojo endurecido) ou se apenas uma borda está conectada (caso nãotiffened). A capacidade de fivela para uma placa de largura b e espessura t,análoga a Eq. (10) para uma coluna, é dada por:

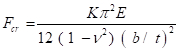(Eq. 11)

O coeficiente de fivela K reflete as condições de limite e a proporção (comprimento-a-largura) da placa. Os valores de K estão amplamente disponíveis em manuais de design estrutural.

1. Obtenha várias peças longas de uma barra de alumínio de 1/4 por 1/4 (6061 ou similar), e corte-as em comprimentos de 72, 60, 48, 36, 24, 12 e 8 in., respectivamente. Rode as duas extremidades das barras para uma circunferência de 1/8 dentro.
2. Meça as dimensões da barra (comprimento, largura e espessura) até os 0,02 in mais próximos.
3. Máquina dois pequenos blocos de aço (2 in. x 2 in. x 2 in.) para ter uma penetração circular muito suave ao longo de um de seus lados para servir como suporte final da coluna. Forneça uma inserção no lado oposto, para que o bloco possa ser fixado na máquina de teste.
4. Insira os blocos e uma amostra de teste na máquina de teste. Certifique-se de alinhar o espécime com o máximo de cuidado possível para eliminar excentricidades.
5. Coloque a máquina de teste no controle de deflexão e programe-a lentamente para aplicar uma deformação de até 0,2 in. e registrar carga e deformação axial. O limite pode ser variado com o comprimento, mas o teste deve ser interrompido quando a carga tiver estabilizado ou quando atingir não mais do que uma redução de carga de 20% da capacidade máxima.
6. Registo a carga máxima atingida e preencha a tabela de resultados.
7. Repita as etapas 1.4 a 1.6 para todas as colunas.

Plote os resultados da tabela como estressamento vs. slenderness (kL/r), juntamente com a curva dada por Eq. 9. Compare seus resultados com os valores previstos. Os resultados experimentais mostram duas regiões distintas. Quando as colunas são relativamente longas, a carga crítica é dada multiplicando Eq. 9 pela área da coluna. À medida que as colunas começam a ficar mais curtas, a carga crítica começa a se aproximar da força do material. Neste ponto, o comportamento muda de um puramente elástico para um inelástico parcial que se aproxima assintóticamente da carga de abóbora da coluna. Quando uma coluna se dobra elástica, a deformação pode se tornar tão grande de repente e desencadear falhas no membro dobrado ou em adjacentes que ficam sobrecarregados à medida que o membro dobrado derrama suas cargas. Assim, no projeto é importante evitar falhas elásticas de fivelas em membros estruturais primários.

Este experimento demonstrou a validade da abordagem Euler para calcular cargas locais de fivelas para colunas simples. Embora o problema se torne muito mais complicado se as condições de limite não forem bem conhecidas, o membro não é prismático, ou se o material não apresenta uma curva de tensão bi-linear, a solução do problema segue o mesmo processo geral. Em muitos casos práticos, não será possível resolver exatamente as equações diferenciais resultantes, mas existem muitas técnicas numéricas que podem ser aplicadas para aproximar a solução desses problemas. A importância do entortar é reconhecida no aforismo da indústria da construção que sustenta que o projeto bem sucedido das estruturas metálicas se baseia em uma boa compreensão das questões de fivela, enquanto o projeto bem sucedido de estruturas de concreto armado baseia-se em um bom detalhamento.

A economia em design exige que o volume do material seja minimizado. Este detalhe é particularmente verdadeiro para a construção de metais e estruturas de pontes, onde os custos dos materiais são uma parte significativa do custo estrutural total. Em geral, a minimização do custo se resume a obter o menor L/r. Para um L fixo, isso significa obter o maior r (ou maior I possível para um dado A), levando ao uso generalizado de membros em forma de W. Para um rfixo, isso significa diminuir L, o que implica o uso de membros bracing. Para uma forma de W, haverá um I_x e I_y, e correspondente (kL/r)_x e (kL/r)_y; para um design ideal, ambos os valores devem estar próximos um do outro, o que muitas vezes é obtido proporcionando mais bracing na direção y. Outra forma de evitar a fivela é adicionar endurecedores, que reduzem os comprimentos de fivela nas placas; exemplos destes incluem endurecedores em vigas de placas de ponte e lábios endurecidos em membros estruturais de forma fria.