Flambage des colonnes d'acier

Source : Roberto Leon, département de génie Civil et environnemental, Virginia Tech, Blacksburg, VA

Dans la conception des travaux de génie civil, il est important de fournir des structures qui ne sont pas seulement sans danger sous des charges inattendues, mais aussi fournissent une performance excellente sous des charges de tous les jours à un coût économique raisonnable. Ce dernier est souvent lié à l’utilisation minimale de matériaux, de la facilité de fabrication et construction rapide dans le domaine. Structures en acier membres peuvent être très économiques à cause de la grande force de la matière et la préfabrication approfondie de leurs membres et les connexions, qui aident à maximiser la vitesse de construction sur le site. Généralement, le squelette d’une structure en acier sera très mince par rapport à un béton armé un. Alors que son comportement en traction est régie principalement par la résistance du matériau, acier en compression est régi par un autre mode de défaillance commun à tous les matériaux-flambage. Ce comportement est facilement démontré en appuyant sur une règle en bois mince, qui, en vertu d’une force de compression, va soudainement se déplacer latéralement et perdent la capacité de charge. Ce phénomène se produit dans n’importe quel membre élancé d’une structure. Dans cet atelier, nous allons mesurer la capacité de flambage d’une série de colonnes élancées en aluminium pour illustrer ce mode de rupture, qui, au fil du temps, a conduit à nombreuses défaillances catastrophiques, dont celui du pont de la rivière au Québec, qui a été érigé en 1918.

Puisque le phénomène de flambement est facilement observable, il était bien connu depuis l’antiquité, mais un aperçu analytique le problème de flambement n’a pas gagné attention jusqu’aux années 1700, lorsque les fondements mathématiques de la physique est devenus des sujets d’étude. Leonhard Euler, un célèbre mathématicien suisse, fut le premier à vous offrir la solution à la charge de flambage d’une colonne avec appui simple en 1742. Euler a formulé sa solution par un raisonnement qu’une colonne parfaitement droite pourrait être en équilibre dans deux configurations : un peu déformé et une déformée (légèrement fléchis position).

Pour la colonne déformée, Euler postule que l’équilibre dans une configuration légèrement pliée dans lequel les moments extérieurs, compte tenus de la charge P art dramatique à une excentricité y, sont équilibrés par les moments internes (M) :

(EQ. 1)

quantité y est le déplacement latéral le long de la longueur z. La première dérivée de y est la pente, et la dérivée seconde de y est la courbure du membre. La résistance interne est proportionnelle à la courbure ou à l’instant interne divisé par la rigidité en flexion (AE), afin que :

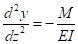(EQ. 2)

Dans cette équation E est le module d’élasticité et I est le moment d’inertie, une propriété géométrique de la section. Son remplacement (EQ. 2) (EQ. 1) et réglage il égal à zéro donne l’équation différentielle traditionnelle de flambage, où y est la déformation horizontale, et k est une variable de substitution utilisée pour simplifier les équations.

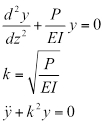(EQ. 3)

Si nous supposons que la déformation de la colonne le long de sa longueur z est donnée par :

(Équation 4)

et que la colonne ait épinglé se termine, et que ces fins ne pas déplacent latéralement par rapport à un autre, puis la condition aux limites à z = 0 et L, le déplacement latéral, est égale à zéro. Par conséquent,

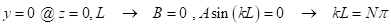(EQ. 5)

où N = 1,2,... La plus petite valeur de N est 1, ce qui correspond à la charge de flambage élastique (P _critique ou P _cr). Pour une colonne avec des extrémités épinglées, (c'est-à-dire avec les extrémités libres de tourner, mais ne traduit pas tant que les conditions limites indiquées ci-dessus) P_cr est donnée par Euler charge de flambage :

(Équation 6)

Il est important de noter que cette équation ne contient-elle pas n’importe quel termes liés à la résistance du matériau, qu’à son module d’élasticité (E), les dimensions et longueur. Le moment d’inertie (I) d’une section composée de pièces rectangulaires est donnée par la somme sur le centre de gravité de la section de deux composantes : le moment d’inertie de chaque rectangle (bd³12) plu sa surface (A) fois son distance entre le centre de gravité de la section entière (d) :

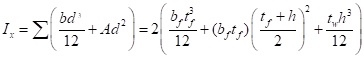(Équation 7)

EQ. 7 met en évidence que la valeur d’I peut être augmentée sensiblement en mettant la plupart des matériaux aussi loin depuis le centre de gravité que possible (c'est-à-dire en maximisant d). Par exemple, pour une superficie totale fixe de 13 po², on pourrait opter pour deux distributions : un seul rectangle de 13 po x 1 po, ce qui donne un total I de 183 po⁴, ou (b) une section en forme de W, avec deux brides de 6,5 x 0,45 po connecté avec une toile de 0,35 po x 19,1 po, soit un total de 761 po⁴. Clairement la forme en W sera une utilisation beaucoup plus efficace de la matière en ce qui concerne la compression, car il fournira plus de 4 fois plus grande capacité flambage. L’AISC W-forme standard d’une superficie de 13 po², un W21x44 (profondeur nominale de 21 po) et un poids de 44 lb par pied fournit un I 843 po⁴ ou 4,5 fois celui de la section rectangulaire.

La relation entre le moment d’inertie (I) et la zone (A) est définie par le rayon de giration (r) :

(EQ. 8)

La capacité de flambage est parfois exprimée comme une contrainte critique (F_cr) en divisant la charge critique de la région :

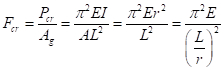(EQ. 9)

Il faut garder à l’esprit qu’il existe certaines limitations inhérentes à la dérivation de l’équation (6) et l’équation (9) en ce qu’ils supposent :

1. Comportement purement élastique et donc ils ne sont valides qu’à concurrence de la limite proportionnelle du matériau.
2. La charge est appliquée au centre de gravité de la colonne, ce qui est difficile à réaliser dans la pratique. Ainsi, des excentricités initiales accidentelles jouera un rôle dans la conception.
3. La colonne est initialement parfaitement rectiligne. Étant donné que les formes en acier sont produits par un processus de laminage, ils auront une cambrure et un coupe-bise (c.-à-d., ils vont être légèrement courbés sur les deux axes principaux). Ces imperfections initiales sont de petite taille, l’ordre de L/1000, mais feront comportement véritable colonne s’écarter de celle d’une colonne idéalisée.
4. Une forme déviée, qui, dans notre cas, a pris la forme d’une fonction trigonométrique (c'est-à-dire, une combinaison de fonctions sinus et cosinus). Dans ce cas, nous avons utilisé effectivement la bonne solution analytique, mais ce n’est pas toujours possible. En général, toute fonction d’approximation de la solution correcte donnera un niveau satisfaisant approximative, mais pas une solution exacte.
5. Conditions de fin idéalisée. Afin de résoudre pour la charge de flambage, les conditions aux limites du problème mathématique ont été établis, et nous avons supposé que la colonne avait épinglé des extrémités. En outre, on a supposé que les extrémités de la colonne ne s’est pas traduit de latéralement par rapport à un autre (par exemple, c’est le cas de sway-empêché, qui se produit dans des cadres contreventés par opposition à l’affaire sway-autorisé, qui se produit dans des cadres contreventés). Dans la vraie vie, ces conditions idéalisées peuvent seulement être approximées.
6. L’absence de toute contraintes résiduelles, qui résultent du refroidissement et des formes en acier de roulement pendant la production. Ces résultats de stress en céder plus tôt que prévu et la perte de moment d’inertie, comme les sections donnant ont un degré d’élasticité de zéro. Diminution de la rigidité de la colonne, la capacité de la colonne est à la baisse, puisque l’équation 1 a EI dans le numérateur.

La seconde, troisième et dernière limites sont généralement traités ensemble comme imperfections initiales et leurs amplitudes correspondent à la tolérance établie, construction et fabrication. Conception de colonne courbes ont été conçues pour atténuer ces problèmes de manière satisfaisante.

Un système structurel et mécanique est censé être sensible si la capacité de charge du système imparfait est sensiblement inférieure à celle du système parfait imperfection. À l’inverse, un système est dit imperfection insensible s’il n’y a aucune perte de capacité portante en raison des imperfections. Une colonne est censée être une colonne parfaite si elle est droite, et la charge est concentrique. Tout cela est impossible dans la pratique, nous sommes chanceux parce que les colonnes sont imperfection insensible et n’aura donc pas une soudaine perte de capacité de charge sous des charges normales. En revanche, sphères et cylindres sont imperfection sensible, et en conséquence, beaucoup de soin il faut pendant la construction des réservoirs (dômes, tours de refroidissement et des réservoirs de stockage) et d’autres structures pour obtenir la géométrie appropriée. L’effet des imperfections est d’accélérer le rythme de la flexion latérale, car ils ont tendance à augmenter les moments de flexion de la colonne.

Les limitations liées à la cinquième hypothèse, que des conditions aux limites, peut être traitée simplement par l’utilisation de la notion d’une longueur effective (kL). La longueur effective facteur k donne la proportion de la longueur entre les points d’inflexion (c.-à-d., les points de zéro moment ou zéro courbure le long de la colonne). Donc, EQ (9) peut être réécrite sous la forme :

(Équation 10)

Le dénominateur (kL/r) est connu comme la finesse de la colonne. Une valeur faible (par exemple, kL/r < 20) est synonyme d’une colonne trapue, ce qui n’est pas très sensible au flambement, alors qu’une valeur élevée (par exemple, kl/r > 100) est synonyme d’une colonne élancée, qui est très sensible au flambage.

Il est à noter que la contrainte critique (σ_cr) pour la conception est coiffée par la limite d’élasticité du matériau (σ_y). Cette contrainte signifie que pour tout donné force d’acier, dire σ_y = F_y = 50 ksi _, il y aura un élancement ci-dessous quel flambage ne se produira pas. Si nous assimilons σ_cr = 50 ksi dans l’équation (10), l’élancement de limite est kl/r < 75,6.

Un autre inconvénient important est que la formulation ci-dessus indique que flambage se produit soudainement que la charge axiale atteint sa valeur critique (P_cr). Mathématiquement, cela indique que le flambage est un problème de bifurcation. En raison des imperfections initiales, excentricités accidentelles et des contraintes résiduelles entre autres facteurs, il y aura une transition entre l’élastique contrainte de flambage et charge de la courge. Le résultat de ces imperfections initiales, c’est que dans la vraie vie, il y aura une transition en douceur entre la courbe de flambement élastique et les États limites de rendement.

À ce stade, il est important de noter que l’instabilité ou le phénomène de flambage en discussion est un des nombreux qui peuvent se produire. Instabilités surviennent au niveau local et mondial. Instabilité de niveau mondiale est lorsque tous les éléments (un élément est défini comme n’importe quelle section rectangulaire qui composent une forme) se déplacent ensemble pendant le flambage. Flambage local se produit lorsqu’un seul des éléments se déplace. Exemples de flambement global sont :

• En flexion flambage, qui est le cas discuté ci-dessus.
• Torsion de flambage, en qui la section sinue sur son centre de gravité longitudinal. Sections qui ont petite rigidité torsionnelle (J) sont sujettes à ce type de défaillance.
• Flexion-torsion ou latéraux-torsion flambage, qui est une combinaison des deux premiers types de flambement global et est le mode prédominant de l’instabilité des poutres.
• Cisaillement de flambage, dans lequel le flambage se produit dans les toiles fines de poutres profondes due à la formation d’un champ de tension dans le sens de la diagonale.

Sections peuvent boucler aussi localement. Ceci est analogue à chaque section de la colonne flambage individuellement comme une assiette. Flambage local est régi par le rapport largeur-épaisseur (b/t) ou l’élancement de la section et les proportions de la plaque (b / a, où a est la longueur). L’élancement dépend de savoir si les deux bords de la plaque sont connectés à une autre section (affaire raidi), ou si seul un côté est connecté (raidisseur cas). La capacité de flambage pour une assiette de largeur b et épaisseur t, analogue à l’équation (10) pour une colonne, est donnée par :

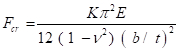(EQ. 11)

Le coefficient de flambement K reflète les conditions aux limites et les proportions (longueur-largeur) de la plaque. Les valeurs de K sont largement disponibles dans les manuels de conception structurale.

1. Pour obtenir plusieurs longs morceaux de 1po. une barre d’aluminium de ¼ po (6061 ou similaire) et coupez-les en longueurs de 72, 60, 48, 36, 24, 12 et 8 po., respectivement. Tour les deux se termine des bars pour une circonférence de 1/8 po.
2. Mesurer les dimensions de la barre (longueur, largeur et épaisseur) à la plus proche à 0,02.
3. Deux petit bloc d’acier de la machine (2 po x 2 po x 2 po) d’avoir un taux de pénétration très lisse ½ po circulaire le long d’un de ses côtés pour servir à l’appui de fin de colonne. Fournir un encart sur le côté opposé, afin que le bloc peut être fixé sur la machine d’essai.
4. Insérer les blocs et une éprouvette dans la machine d’essai. Veillez à aligner le spécimen aussi soigneusement que possible afin d’éliminer les excentricités.
5. Définir la machine d’essai contrôle de déviation et la programmer à appliquer lentement une déformation maximale de 0,2 po et charge record et une déformation axiale. La limite peut être modifiée à la longueur, mais le test ne doit être arrêté lorsque la charge s’est stabilisée ou lorsqu’il a atteint pas plus qu’une réduction de 20 % de la charge de la capacité maximale.
6. Enregistrement de la charge maximale atteint et remplir le tableau de résultats.
7. Répétez les étapes 1,4 à 1,6 pour toutes les colonnes.

Tracer les résultats de la table comme le flambage souligne vs élancement (kL/r), ainsi que la courbe donnée par l’équation 9. Comparer vos résultats avec les valeurs prédites. Les résultats expérimentaux montrent deux régions distinctes. Lorsque les colonnes sont relativement longs, la charge critique est donnée en multipliant l’équation 9 de la zone de la colonne. Comme les colonnes commencent à se raccourcir, la charge critique commence à approcher la résistance du matériau. À ce stade, le comportement passe d’un purement élastique pour un d’inélastique partiel qui s’approche asymptotiquement la charge de courge de la colonne. Lorsqu’une colonne boucles élastiquement, déformation peut devenir chaque grand soudainement et déclencher des échecs soit dans le membre bouclée adjacents qui deviennent surchargés comme le membre bouclée jette ses charges. Ainsi, dans la conception, il est important de prévenir les défaillances flambement élastiques dans les éléments de structure primaires.

Cette expérience a démontré la validité de la démarche d’Euler pour le calcul des locale de flambage des charges pour les colonnes simples. Bien que le problème devient beaucoup plus compliqué si ou l’autre des conditions aux limites ne sont pas bien connues, le membre n’est pas prismatique, ou si le matériel ne présente pas une courbe contrainte-déformation bi-linéaire, la solution du problème suit le même processus général. Dans de nombreux cas pratiques, il ne sera pas possible de résoudre les équations différentielles qui en résulte exactement, mais il existe de nombreuses techniques numériques qui peuvent être appliquées pour se rapprocher de la solution à ces problèmes. L’importance de flambage est reconnue dans l’aphorisme de l’industrie de construction qui maintient que le design réussi des structures en acier repose sur une bonne compréhension de flambage questions, tandis que la conception de structures en béton armé repose sur la bonne exposant en détail.

L’économie de conception exige que le volume des documents être minimisé. Ce détail est particulièrement vrai pour la construction en métal et de structures de pont, où les coûts de matériaux sont une partie importante des coûts structurels. En général, réduire au minimum les coûts se résume à obtenir le plus bas L /r. Pour un L fixe, cela signifie obtenir le plus grand possible r (ou plus grand j’ai pour un A donné), d'où l’utilisation généralisée des membres en forme de W. Pour un fixe r, cela signifie diminuer L, ce qui implique l’utilisation de membrures de contreventement. Pour une forme en W, il y aura un I_x et j’ai_yet correspondants (kL/r)_x et_yde (kL/r) ; pour une conception optimale, ces deux valeurs doivent être proche de l’autre, qui sont souvent obtenus en fournissant des renforts plus dans la direction y. Une autre façon de prévenir le flambage est d’ajouter des raidisseurs, qui réduisent les longueurs de flambement en plaques ; Ces exemples de raidisseurs en pont poutres et les lèvres de raidissement en froid-forme de charpente.