Esfuerzo torsional
Visión general
Fuente: Nicolás Timmons, Asantha Cooray, PhD, Departamento de física & Astronomía, Facultad de ciencias física, Universidad de California, Irvine, CA
El objetivo de este experimento es conocer los componentes del esfuerzo de torsión y equilibrar múltiples pares en un sistema para alcanzar el equilibrio. Igual que cómo una fuerza provoca aceleración linear, esfuerzo de torsión es una fuerza que provoca una aceleración rotacional. Se define como el producto de una fuerza y la distancia de la fuerza del eje de rotación. Si la suma de los pares en un sistema es igual a cero, el sistema no tendrá ninguna aceleración angular.
Principios
Esfuerzo de torsión se define como el producto de una fuerza aplicada a cierta distancia del eje de rotación:
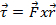 , (Ecuación 1)
, (Ecuación 1)
donde 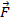 es la fuerza aplicada y
es la fuerza aplicada y 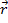 es la distancia al eje de rotación. Esfuerzo de torsión tiene unidades de fuerza multiplicado por distancia y por lo tanto se mide en Newton metros. Porque el par es un vector, tiene magnitud y dirección. La dirección del esfuerzo de torsión es perpendicular al plano de los componentes de fuerza y distancia. La dirección puede ser determinada usando la mano derecha. Extender el dedo de puntero en la dirección del primer componente. Extender el dedo medio en la dirección del segundo componente. Una vez hecho esto, la dirección del pulgar extendido es la dirección del esfuerzo de torsión. Un ejemplo es una llave de apretar un perno. Una fuerza es aplicada en el extremo de la llave, cierta distancia desde el perno, que proporciona un par motor para girar el tornillo en su lugar. Más largo es la distancia
es la distancia al eje de rotación. Esfuerzo de torsión tiene unidades de fuerza multiplicado por distancia y por lo tanto se mide en Newton metros. Porque el par es un vector, tiene magnitud y dirección. La dirección del esfuerzo de torsión es perpendicular al plano de los componentes de fuerza y distancia. La dirección puede ser determinada usando la mano derecha. Extender el dedo de puntero en la dirección del primer componente. Extender el dedo medio en la dirección del segundo componente. Una vez hecho esto, la dirección del pulgar extendido es la dirección del esfuerzo de torsión. Un ejemplo es una llave de apretar un perno. Una fuerza es aplicada en el extremo de la llave, cierta distancia desde el perno, que proporciona un par motor para girar el tornillo en su lugar. Más largo es la distancia 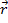 , cuanto mayor sea el esfuerzo de torsión, como puede verse en la ecuación 1. Puede reducir significativamente la fuerza necesaria para girar un objeto simplemente aumentando la longitud de la fuerza al eje de rotación.
, cuanto mayor sea el esfuerzo de torsión, como puede verse en la ecuación 1. Puede reducir significativamente la fuerza necesaria para girar un objeto simplemente aumentando la longitud de la fuerza al eje de rotación.
Un esfuerzo de torsión en un sistema causará una aceleración angular en ese sistema:
 . (Ecuación 2)
. (Ecuación 2)
Aquí,  es la aceleración angular y
es la aceleración angular y  es el momento de inercia de ese sistema. Este es el equivalente rotacional de la segunda ley de Newton,
es el momento de inercia de ese sistema. Este es el equivalente rotacional de la segunda ley de Newton, 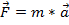 , con masa substituido con el momento de inercia y aceleración sustituida con la aceleración angular.
, con masa substituido con el momento de inercia y aceleración sustituida con la aceleración angular.
Este experimento incluye un palo de metro que es capaz de girar libremente alrededor de su eje, como se muestra en la figura 1.

Figura 1: Montaje Experimental.
Pesos se unen a diferentes distancias del eje de rotación, que hará un esfuerzo de torsión en el sistema. Si los esfuerzos de torsión en ambos lados se equilibran, el palillo del metro no debe girar del resto. Para examinar el par de un peso o una combinación de pesos, una escala de fuerza puede conectarse al otro lado. La fuerza que lee la escala multiplicada por la distancia de la escala del eje de rotación será igual al par de los pesos.
Procedimiento
1. usando dos pesos para equilibrar el rayo.
- Comience conectando un peso de 200 g para el primer gancho a la derecha. A continuación, conecte un peso de 200 g para el primer agujero a la izquierda. Si se libera del resto, la viga no debe girar.
- Retire el peso de 200 g del lado izquierdo. Determinar utilizando la ecuación 1 donde un peso de 100 g tendría que colocarse para equilibrar el par de la derecha. Coloque el peso y confirman la predicción.
2. con tres pesas para equilibrar el rayo.
- Conectar un peso de 100 g para el primer gancho a la derecha. Coloque un peso de 100 g en el tercer gancho a la derecha.
- Determinar dónde colocar un peso de 200 g en el lado izquierdo para equilibrar los pares de apriete.
- Determinar dónde colocar un peso de 100 g en el lado izquierdo para equilibrar los pares de apriete.
3. utilizar múltiples pesos para equilibrar el rayo.
- Conectar un peso de 200 g en el cuarto gancho en el lado derecho.
- Utilizando cualquier combinación de encontrar pesos de 100 g y 200 g tres maneras en que puede equilibrarse el par de la derecha a la izquierda.
- Con el peso de 200 g todavía conectado al cuarto gancho en el lado derecho, conectarse a una escala de fuerza el primer gancho a la izquierda y tire hasta que quede en equilibrio. Asegúrese de mantener la escala de la fuerza perpendicular a la viga. Registro de la fuerza. Hacer esto para cada gancho en el lado izquierdo y anote los valores.
- Con el peso de 200 g todavía conectado al gancho de cuarto a la derecha, utilice un transportador para girar el haz de 30°. Coloque la escala de la fuerza en el tercer gancho a la izquierda y el registro de la fuerza. Repita para 60°.
Resultados
Paso 1.2: Conecte un peso de 100 g en el segundo agujero a la izquierda.
Paso 2.2: Conecte el peso de 200 g en el segundo agujero a la izquierda.
Paso 2.3: Conecte el peso de 100 g en el cuarto agujero a la izquierda.
Paso 3.2: Existen seis maneras diferentes:
1) 200 g - 4 orificios deth
2) agujero de 3rd 200 g - 1st agujero, 200 g-
3) agujero de 3rd 100 g - 2nd agujero, 200 g-
4) 100 g - 1st agujero, agujero de 3rd 200 g - 2nd agujero, 100 g-
5) 200 g - 2nd el agujero, 100 g - 4 orificios deth
6) orificio 3rd 100 g - 1st agujero, 100 g - 100 g - 4 orificios deth
Tabla 1. Resultados para pasos 3.3 y 3.4.
| Anzuelo # | Fuerza
(N) |
Fuerza a 30°
(N) |
De la fuerza en 60°
(N) |
| 1 | 8 | - | - |
| 2 | 4 | - | - |
| 3 | 2.7 | 2.3 | 1.3 |
| 4 | 2 | - | - |
Estos resultados confirman las predicciones de la ecuación 1. Cada peso conectada a la viga proporciona un esfuerzo de torsión en el sistema. Mientras pesos por un lado provocan una torsión en una dirección, pesos en el otro lado causan una torsión en la dirección opuesta. Según la ecuación 2, cuando la suma de los esfuerzos de torsión en la viga es igual a cero, la viga no girará cuando suelte el resto. En cada parte del experimento, cuando la viga está en equilibrio, los esfuerzos de torsión deben agregar hasta cero.
Aplicación y resumen
Como se mencionó anteriormente, una sencilla aplicación de torsión está utilizando una llave para apretar un tornillo. La cosa importante a recordar es que par tiene dos componentes. Si es difícil apretar un tornillo con la llave en la mano, un trabajador tiene dos opciones. Puede aplicar más fuerza o simplemente obtener una llave más larga. Generalmente, esta última es la opción más fácil.
Cuando un coche comercial cita algún valor de esfuerzo de torsión, es una buena idea prestar atención. Como puede verse por la ecuación  , esfuerzo de torsión es lo que hace que las ruedas de un coche acelerar. La más par motor, aceleración más.
, esfuerzo de torsión es lo que hace que las ruedas de un coche acelerar. La más par motor, aceleración más.
Un subibaja en el parque infantil es una aplicación perfecta del esfuerzo de torsión. El haz gira alrededor del fulcro y el esfuerzo de torsión es proporcionado por las personas sentadas en cada extremo. Si una persona tiene más masa, entonces el esfuerzo de torsión de ese lado será mayor y la persona al otro lado se levantarán para arriba. Para conseguir esa persona hacia abajo, la persona en el suelo proporciona un par empujando hacia arriba con las piernas para contrarrestar la fuerza de su, peso y a su vez se levantó.
En este experimento, examinaron los dos componentes principales del esfuerzo de torsión. Esfuerzo de torsión es el producto de una fuerza y la distancia entre la fuerza y un eje de rotación. Mediante la colocación de diversos pesos en diferentes posiciones en un haz giratorio, se crearon diferentes cantidades de esfuerzo de torsión. El peso más pesado correspondió a una fuerza más grande y por lo tanto un mayor par. Colocando pesos más lejos del eje de rotación crea un mayor brazo de palanca, que se tradujo en un mayor par que si el mismo peso se había colocado más cercano al eje de rotación. Cuando el torque total sobre la viga es igual a cero, el sistema estaba en equilibrio.
Tags
Saltar a...
Vídeos de esta colección:

Now Playing
Esfuerzo torsional
Physics I
26.2K Vistas

Las leyes del movimiento de Newton
Physics I
76.9K Vistas

Fuerza y aceleración
Physics I
79.6K Vistas

Vectores en múltiples direcciones
Physics I
182.7K Vistas

Cinemática y movimiento de proyectiles
Physics I
73.1K Vistas

Ley de la gravitación Universal de Newton
Physics I
192.7K Vistas

Conservación del momento
Physics I
43.6K Vistas

Fricción
Physics I
53.1K Vistas

Ley de Hooke y el movimiento armónico simple
Physics I
61.6K Vistas

Diagramas de equilibrio y de cuerpo libre
Physics I
37.6K Vistas

Inercia rotacional
Physics I
43.8K Vistas

Momento angular
Physics I
36.6K Vistas

Energía y trabajo
Physics I
50.4K Vistas

Entalpía
Physics I
60.6K Vistas

Entropía
Physics I
17.8K Vistas
ACERCA DE JoVE
Copyright © 2025 MyJoVE Corporation. Todos los derechos reservados