熵

熵是"国家财产"，即只取决于系统的当前状态的数量。状态属性的数量不依赖的系统到达其当前状态的路径。因此，最有用的方式来量化国有财产是衡量其更改。

在熵S变化定义为:

Δ = Q / T，（方程 1）

在哪里 Q提供给系统的热量和T是系统的温度。在热力学中，热，工作，像被定义为能量转移。热是能量从一个物体转移到另一个由于温度的差异。考虑洗澡的冰和水在 0 ° c。如果你提供的热量，以冰水浴，一些冰就会融化，和可用的水分子状态数目将增加量大，被添加到系统的散热量成正比。熵然后将增加比例这一数额。由牛顿首先介绍了在不同温度下的两个对象之间的关系。

牛顿冷却定律的一些物体的温度变化率是正比于其自身温度和其周围环境的温度之间的区别。在温度T放置在一个封闭的系统，在温度T_f，这种变化温度作为时间的函数对象t是由微分方程描述的:

dT/dt =-k (T-T_f )， （公式 2）

在哪里 k是一个常数，取决于对象和其周围环境的特点。方程 1等效地写成:

-k dt = dT / (T-T_f )。（方程 3）

结合双方给出:

-k t = 日志 (T-T_f ) + 登录 C.（方程 4）

将幂指函数应用到这两个方程的两边，然后重新排列给:

T-T_f = C e^-kt 。（方程 5）

如果所讨论的对象是在初始温度T_我当时t = 0:

T_我-T_f = C.（方程 6）

因此，温度作为时间的函数是:

期望值 = T_f + (T_我-T_f ) e^-kt 。（方程 7）

因此，当一个热的物体放在一个凉爽的封闭系统，它的温度将降低以指数的速度。在这个封闭的系统，从热的物体Q热将增加的凉爽的环境温度，从而增加可用的国家的数目。因此，变化熵，ΔS，是积极和非零。

680 毫升的水代表结果如表 1所示。使用表中的数据点和求解方程 7发现冷却常数k 。后 35 分钟， T(35) = 50.6。初始温度是 100 ° C 和数据收集，停止在 28.5 ° c。使用这些变量给出了下面的公式来获得克:

50.6 = 28.5 + (100-28.5) e^{-k 35}。（方程 8）

解决因k值k = 0.034。此冷却常数的曲线显示为灰色虚线在图 1中，和从实验数据点。方程 6的函数形式非常紧密匹配的实验结果。

当水冷却时，熵减小，从可用的水分子减少状态数量。在房间里空气的熵增加，因为水的烧杯将热量传递到它; 周围的空气分子水的总熵 + 空气系统的增加。现在热空气分子可以占领的国家的数目是远远高于之前热水被引入到房间里。

在微分形式，可以使用大众，比热c，之间的关系计算热 dQ添加或删除从水和温度变化:

dQ = mc dT， (方程 9)

其中c是已知 4.18 J/(gK) 为水。水的熵的变化然后是:

ΔS_水=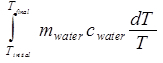

= m_水 c_水ln (_最后T/T_初始)。（方程 10）

使用转换到开尔文作为 K = ° C + 273.15 中的水的熵变计算为:

ΔS_水= 680 g * 4.18 J /(g K) * ln [(28.5 + 273.15)/（100 + 273.15）]

=-604 J/K。

周围的空气温度是恒定在 20.4 ° C，因此这是一个等温过程。空气的熵变化然后是:

ΔS_空气= ，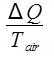

其中Q是由水，给出了方程 9所放出的热量。空气的熵的变化然后计算如下:

ΔS_空气=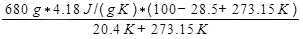

= 3337 J/K。

水 + 空气的熵的总变化系统，ΔS_tot，是水和空气的熵的个人变化的总和:

ΔS_tot = δ_水+ δ_空气 (方程 11)

=-604 J/k + 3337 JK

= 2733 J/K。

表 1。温度记录试验过程中。

时间 (min s)	水的温度 （° C）
0 0	99.6
1 10	97.1
1 50	94.2
2 30	91.8
3 22	89
4 05	87.2
5 08	82.7
6 05	82.4
8 25	78
9 15	76.5
10 15	74.6
11 38	72.7
12 58	70.7
13 58	69.2
15 15	67.7
16 55	65.8
18 38	64
20 25	62.3
24 02	58.8
25 45	57.3
34 45	50.6
40 50	47.4
44 30	45.9
49 59	43.6
53 42	42.4
60 01	40.2
64 20	39.5
76 37	37
103 50	32.1
116 41	30.3
122 46	29.6
134 11	28.5

图 1.温度与时间的阴谋。蓝色的点表示的实验数据，和虚线表示基于牛顿冷却定律的理论数据。

一副耳机保持在一个袋子里总是倾向于成为纠结在一起，这是由携带袋左右，引起的熵增加。它是必要做他们工作向联合国结耳机和降低的熵 （这可以被认为是一个"可逆过程"）。物理定律所允许的最高效率热机循环是卡诺循环。第二定律并不是所有的热量提供给热引擎可以用于做的工作。卡诺效率上的热，可以用分数设置的极限值。周期由两个等温过程，其次是两个绝热过程组成。冰箱，这是本质上只是一种热泵，也是一个经典的例子，第二定律。冰箱热从一个位置移动在较低温度 （"源"） 到另一个位置使用机械工作的较高温度 （"散热器"）。根据第二定律，热不能自发地从流向冷的位置一热;因此，工作 （能量） 是必需的制冷。

牛顿冷却定律证明了烧杯装满了水在 100 ° C，降温至室温，导致水-空气系统的熵增加。通过测量水的温度作为时间的函数在 135 分钟内，就能确认冷却水是指数形式。水样的冷却常数被发现通过求解冷却方程使用收集到的数据。