Cross Cylindrical Flow: Measuring Pressure Distribution and Estimating Drag Coefficients

The non-dimensional pressure coefficient, C_p, for an arbitrary position in ideal potential flow theory at any angular position, θ, on the surface of a circular cylinder is given by the following the equation:

The pressure coefficient C_p is defined as:

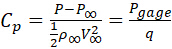
where P is the absolute pressure, P_∞ is the undisturbed free-stream pressure, P_gage = P − P_∞ is the gage pressure, and  is the dynamic pressure, which is based on the free-stream density, ρ_∞, and airspeed, V_∞.

The flow pattern predicted by ideal potential flow theory is shown in Figure 1. The flow is symmetrical, and therefore there is zero net drag force. This is called D'Alembert's Paradox [1].

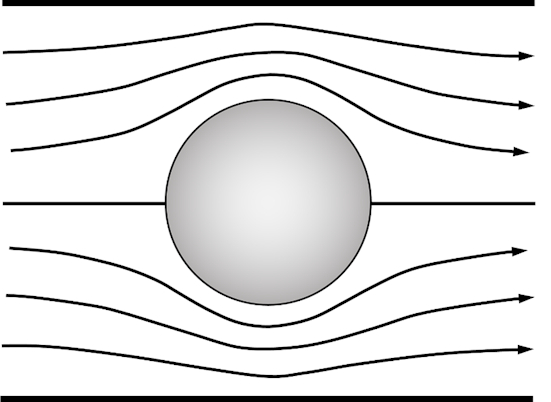
Figure 1. Flow pattern of an ideal cross-cylindrical flow in a wind tunnel.

However, a net zero drag force is not expected under real flow conditions. The drag force of a cylinder, F_D, per unit length of the cylinder due to pressure differences is given by:

The integration is taken along the perimeter of the cylinder.

In this experiment, gage pressure measurements are collected from 24 pressure ports along the cylinder. Then, the above equation can be numerically evaluated using the measured gage pressure as follows:

where P_gagei is the gage pressure at the location of θ_i, θ_i is the angular position, r is the radius of the cylinder, and 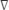θ is the angular distance between adjacent ports, which is 15°. The gage pressure is determined using a manometer panel with 24 independent columns, the gage pressure is determined using the following equation:

where Δh is the height difference of the manometer in reference to the free-stream pressure, ρ_L is the density of the liquid in the manometer, and g is the acceleration due to gravity. Once the drag force is obtained, the non-dimensional drag coefficient C_D can be determined through:

where d = 2r is the diameter of the cylinder.

Remembering D'Alembert's Paradox, the drag force is due to the neglected effects of viscosity. First, a boundary layer develops along the cylinder as a result of viscous forces. These viscous forces cause skin-friction drag. Second, the cylinder is a bluff (non-streamlined) object. This creates flow separation and a low-pressure wake behind it and causes a larger drag force due to the pressure differential. Figure 2 displays several typical flow patterns that are observed experimentally. Real flow patterns rely on the Reynolds number, Re, which is defined as:

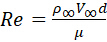
where the parameter μ is the dynamic viscosity of the fluid.

Figure 2. Various types of flow patterns over a cylinder.

Experimental results for the clean and disturbed cylinder are shown in Tables 1 and 2, respectively. The data can be plotted in a graph of the pressure coefficient, C_p, versus angular position, θ, for ideal and real flow as shown in Figure 6.

Pressure port #	Position angle q (°)	Pgage from manometer readings (in. water)	Calculated pressure coefficient Cp
0	0	1.7	1.00
1	15	1.4	0.83
2	30	0.0	0.01
3	45	-1.7	-0.98
4	60	-2.7	-1.57
5	75	-3.7	-2.15
6	90	-3.3	-1.92
7	105	-3.0	-1.74
8	120	-3.2	-1.86
9	135	-3.2	-1.86
10	150	-3.3	-1.92
11	165	-3.5	-2.03
12	180	-3.4	-1.97

Table 1. Experimental results for the clean cylinder. Due to symmetry, only data for ports number 0-12 are shown.

Pressure port #	Position angle q (°)	Pgage from manometer readings (in. water)	Calculated pressure coefficient Cp
0	0	1.8	1.05
1	15	1.6	0.93
2	30	0.6	0.35
3	45	-1.3	-0.73
4	60	-2.9	-1.69
5	75	-4.0	-2.31
6	90	-4.0	-2.33
7	105	-1.7	-0.99
8	120	-1.5	-0.89
9	135	-1.4	-0.84
10	150	-1.4	-0.84
11	165	-1.5	-0.87
12	180	-1.4	-0.84

Table 2. Experimental results for the disturbed cylinder. Due to symmetry, only data for ports number 0-12 are shown.

Figure 6. Pressure coefficient distribution, C_p, vs angular position, θ, between ideal and real flow.

At the stagnation point, θ = 0°, C_p reaches its maximum value of C_p = 1. For θ < 60°, the pressure coefficient distribution is similar for all three curves. This is where the laminar boundary layer flow is attached to the surface of cylinder. For θ > 60°, the two experimental flow patterns deviate from the ideal flow; they form a low-pressure region in the back of the cylinder, which is filled with turbulent vortices and eddies. This is the called the wake region. It is the pressure difference between the front and the back of the cylinder that causes the large drag that is observed in cross cylindrical flow.

Despite the similarity in flow patterns between the clean cylinder and disturbed cylinder, there are also differences. The disturbed flow tends to wrap around the cylinder more prior to flow separation, and it also has a higher back pressure. This causes less drag, which is verified by the drag calculations. This occurs because the laminar flow in the front of the cylinder has a tendency to flow straight and it is difficult for the flow to wrap around the cylinder. For the disturbed cylinder, the flow immediately transitions into turbulent flow and thus can wrap around the cylinder more than the clean cylinder.

Flow Configurations	Drag coefficient, CD
1. Clean cylinder	1.68
2. Disturbed cylinder	0.78

Table 4. Drag coefficient, C_D (Reynolds number Re = 1.78 x 10⁵).

The drag coefficient C_D for clean cylinder at 60-mph airspeed or Re = 178,000 has been evaluated experimentally and is approximately 1.5 [2], which is close to the value of 1.68 that was obtained in this experiment for a clean cylinder.

From previous experimental results [2], the drag coefficient C_D drops at Re = 3 x 10⁵. This is because the transition from laminar flow to turbulent flow occurs naturally even with a smooth cylinder. In the experiment, the turbulent flow transition is observed by simply taping a 1-mm diameter string to the surface of the cylinder. Thus, a lower drag coefficient C_D of only 0.78 is obtained for the disturbed cylinder.

Cross cylindrical flow has been investigated theoretically and experimentally since the 18th century. Finding the discrepancies between the two allows us to expand our understanding of fluid dynamics and explore new methodologies. Boundary layer flow theory was developed by Prandtl [3] in early 20th century, and it is a good example of the extension of inviscid flow to viscid flow theory in solving D’Alembert’s Paradox.

In this experiment, the cross cylindrical flow was investigated in a wind tunnel and the 24 ports of pressure measurement were made to find the pressure distribution along the surface of the cylinder. The drag coefficient was calculated and it agrees well with other sources. The manipulation of the flow to trigger turbulent boundary flow at relative low Reynolds number was also demonstrated.