Quenching and Boiling
Overview
Source: Alexander S Rattner, Sanjay Adhikari, and Mahdi Nabil; Department of Mechanical and Nuclear Engineering, The Pennsylvania State University, University Park, PA
Controlled heating followed by rapid cooling is an important element of many materials processing applications. This heat-treating procedure can increase material hardness, which is important for cutting tools or surfaces in high wear environments. The rapid cooling stage is called quenching, and is often performed by immersing materials in a fluid bath (often water or oil). Quenching heat transfer can occur due to forced convection - when the action of rapidly moving material through coolant drives the heat transfer process, and due to free convection - when the reduced density of hot fluid near the material surface causes buoyancy-driven circulation and heat transfer. At high material temperatures, the coolant can boil, leading to increased heat transfer effectiveness. However, when extremely hot materials are quenched, they can be blanketed in relatively low thermal conductivity coolant vapor, leading to poor heat transfer.
In this experiment, quenching heat transfer will be measured for a heated copper cylinder, which is representative of small heat-treated parts. The transient sample temperature profile will be measured during quenching and compared with theoretical results for free convection heat transfer. Boiling phenomena will also be investigated qualitatively.
Principles
The process of quenching heat transfer is fundamentally transient. In general, the temperature distribution can vary in space and time inside a cooled material sample. However, if internal conduction thermal resistance is small compared with external thermal resistance from the sample surface to the surrounding fluid (convection), the sample can be assumed to have nearly uniform temperature at any instant, simplifying analysis. This condition can be expressed in terms of the Biot number (Bi), which compares internal conduction resistance to external convection resistance. Generally, when Bi < 0.1, internal heat transfer resistance can be assumed negligible compared to external heat transfer resistance.
 (1)
(1)
Here, h is the external convection coefficient, ks is the thermal conductivity of the sample, and Lc is a characteristic length scale of the sample. h can be predicted using heat transfer models and curve fits published in the literature for different conditions and fluids. In this experiment, h will be measured and compared with results predicted with published models (see Representative Results section).
For the copper cylinder considered here (k = 390 W m-1 K-1, diameter D = 9.53 mm, length L = 24 mm), the characteristic length scale is D/2 = 4.8 mm. Assuming a maximum convection coefficient of h = 5000 W m-2 K-1, the peak Biot number would be 0.06. As this number is small (< 0.1), it is reasonable to assume that internal conduction resistances are negligible, and the sample has uniform temperature. At higher Bi values, a more complicated analysis is needed that accounts for temperature variation in the material.
Assuming a uniform-temperature sample, the heat transfer rate can be modeled by balancing internal energy loss from the sample with the convective heat removal rate from Newton's law of cooling. This approach is called a lumped capacitance analysis.
 (2)
(2)
Here, m is the sample mass (15 g), c is the specific heat of the sample material (385 J kg-1 K-1 for copper), Ts is the sample temperature, As is the sample surface area (8.6 × 10-4 m2), and  is the surrounding fluid temperature.
is the surrounding fluid temperature.
To predict the cooling rate (dTs/dt) during quenching, the convection coefficient (h) must also be predicted. If the sample is below the fluid boiling temperature and held stationary in a pool of coolant, then heat is primarily removed by free convection. In this mode, circulation and cooling is produced by the buoyancy-driven rising of heated fluid near the sample. Greater sample-to-fluid temperature differences result in increased circulation rates.
If the sample temperature is above the boiling point, vapor can be generated at the surface, resulting in significantly higher cooling rates. During boiling, vapor bubbles form and grow from small imperfections (nucleation sites) on the hot surface. At higher surface temperatures, more nucleation sites become active, resulting in greater convection coefficients and higher heat transfer rates. However, at very high temperatures, the relatively low conductivity vapor cannot be removed fast enough. This results in the boiling crisis, in which the surface cooling is limited due to vapor insulation, reducing the heat transfer rate.
Procedure
NOTE: This experiment uses flame heating. Ensure that a fire extinguisher is on hand and that no flammable materials are near the experiment. Follow all standard precautions for fire safety.
1. Fabrication of sample for quenching (see photograph, Fig. 1)
- Cut a small length (~24 mm) of 9.53 mm diameter copper rod. Drill two small holes (1.6 mm diameter) about halfway into the rod near the two ends. These holes will be the thermocouple wells. As the holes and thermocouples are relatively small, we can assume they have minimal effect on the overall heat transfer behaviour.
- Use high temperature epoxy (e.g., JB Kwik) to affix high temperature thermocouple probes into the two holes. Ensure that the thermocouple probe tips are pressed into the center of the copper sample as the epoxy sets.
- Set up a water container as a quenching bath. Insert a third reference thermocouple into the bath near where the sample will be quenched.
- Connect the three thermocouples to a data acquisition system. Set up a program (in LabVIEW for example) to log transient temperature measurements to a spreadsheet.

Figure 1: a. Photograph of instrumented copper sample in cooling water bath. b. Heating copper sample.
2. Performing experiment
- Position a Bunsen burner or chafing fuel canister next to the quenching bath. Light the flame.
- From a safe holding distance, gradually warm the sample over the flame (to ~50°C recommended for the first experiment). The sample can be held by the thermocouple leads (Fig. 1b).
- Start logging the thermocouple data to file, and immerse the sample in the quench bath. Hold the sample steady so that forced convection heat transfer is minimal. Stop recording temperature data once the sample approaches within a few degrees of the bath temperature.
- Repeat this procedure for progressively higher initial sample temperatures (up to ~300°C). For cases above 100°C, observe the boiling behavior after quenching the sample.
3. Data Analysis
- For the logged temperature measurements, record the average sample temperature at each time as the arithmetic mean of the two embedded thermocouple readings.
- Calculate the sample cooling rate at each logged time j as
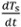 = (Ts,j+1-Ts,j)/(tj+1-tj) (values will be negative). Here, tj is the time of each logged reading. It may be helpful to smooth these cooling rate curves by performing a running average with a sample window of 2-3 readings.
= (Ts,j+1-Ts,j)/(tj+1-tj) (values will be negative). Here, tj is the time of each logged reading. It may be helpful to smooth these cooling rate curves by performing a running average with a sample window of 2-3 readings. - Calculate the experimental heat transfer coefficients h with Eqn. 2 using the cooling rate from Step 3.2, and measured bath (T∞) and sample temperatures (Ts). How do these heat transfer coefficients compare with predicted values (Eqn. 4, see Results)?
- For a case with initial temperature below 100°C, use the initial experimental temperature measurement and numerically integrate Eqn. 2 to predict the cooling over time. Use Eqn. 4 to predict the convection coefficient at each time. Compare this curve to measured values. For numerical time step size Δt (e.g., 0.1 s), the temperature can be integrated as:
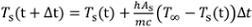 (3)
(3)
Results
Photographs of boiling at different initial sample temperatures (Ts,0) are presented in Fig. 2. At Ts,0 = 150°C vapor bubbles form and stay attached to the sample. At Ts,0 = 175°C bubbles detach and float into the water. At 200°C, more bubbles are generated, and further increases are observed at higher temperatures. Boiling crisis type events (e.g., whole sample being surrounded by persistent vapor) are not observed due to the low bulk fluid temperature (~22°C).
When the sample temperature is below the boiling temperature of the coolant (100°C), single-phase free convection models can be applied to predict the convection coefficient. The free convection heat transfer rate depends on the fluid Prandtl number (Pr), which is the ratio of viscosity to thermal diffusivity (Pr = 6.6 for water at room temperature) and the Rayleigh number (Ra), which is a measure of natural convection transport:
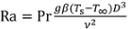 (4)
(4)
Here, g is the gravitational acceleration (9.81 m s-2), β is the thermal expansion coefficient of the fluid (relative change in density with temperature, 2.28 × 10-4 K-1 for water), and ν is the fluid kinematic viscosity (9.57 × 10-7 m2 s-1 for water). As an example, for the 9.5 mm diameter sample at Ts = 75°C in water at T∞ = 22°C, the Rayleigh number is Ra = 7.44 × 105.
For a horizontal cylinder in single-phase free convection heat transfer, a widely used convection formula (based on curve fits to empirical data) is presented in Equation 4.
 (5)
(5)
Here, k is the fluid thermal conductivity (0.60 W m-1 K-1 for water). The formula gives the Nusselt number (Nu), the dimensionless convection heat transfer coefficient. It can be converted to the dimensional heat transfer coefficient (h in units W m-2 K-1) by multiplying by k/D. For the example case with Ra = 7.44 × 105, this model predicts Nu = 16.4 and h = 1040 W m-2 K-1.
In Fig. 3, measured instantaneous convection coefficients are compared with theoretical free convection values from Equation 4. Qualitatively close agreement is observed at lower surface temperatures (Ts-T∞ < 80 K). At higher sample temperatures, boiling occurs and measured heat transfer coefficient values significantly exceed the single-phase free convection predictions. The convection coefficient increases sharply with sample temperature at boiling conditions. This increase is due to the greater number of active nucleation sites at higher surface temperatures.
In Fig. 4, measured and predicted sample cooling curves are presented for a case with initial temperature 42.5°C. Initially, the experimental temperature curve decays quicker. This may be due to forced convection effects from inserting the sample into the bath. Over time, slight oscillations in the measured curve are observed, possibly due to motion of the person holding the sample. Later, the experimental and predicted temperature curves match well.

Figure 2: Photographs of boiling phenomena on quenched sample at increased initial temperature (T0)
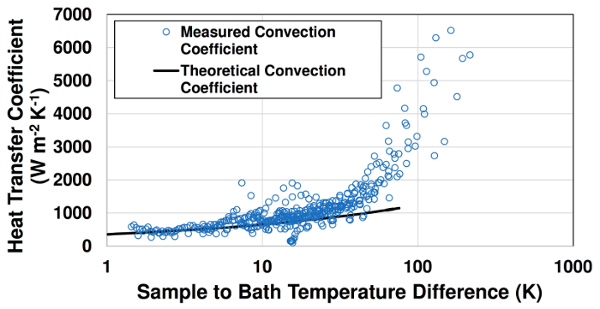
Figure 3: Comparison of measured free convection and boiling convection coefficients with theoretical free convection values
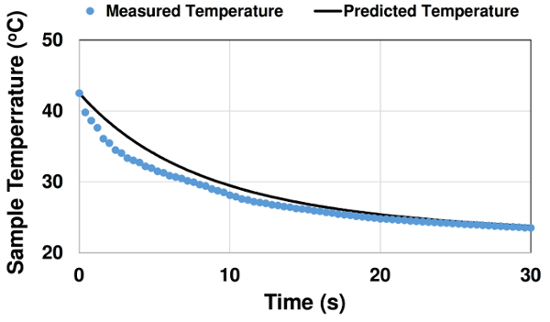
Figure 4: Comparison of measured and predicted cooling curve for case with initial temperature T0 = 42.5°C
Application and Summary
This experiment demonstrated the process of transient heat transfer during quenching. The temperature of a material sample was tracked as it was rapidly cooled in a water bath. The convection coefficients and temperature profiles over time were compared with theoretical values for free convection cooling. Boiling phenomena were also discussed and observed for high initial sample temperatures. Information from such experiments and demonstrated modeling approaches can be applied to understand and design heat transfer processes for manufacturing and material heat treating.
Rapid quenching cooling is often employed in heat-treating tools. Certain steel alloys can be annealed (heated and gradually cooled) to reduce hardness for machining and working. They can then be heated and rapidly cooled to achieve high hardness for cutting other materials (e.g., files, saw blades) or in high wear applications (e.g., hammer heads, punches). Additional heat treating operations can improve toughness to prevent brittle failure.
More generally, fast transient heating and cooling is found in many applications. For example, computer processors heat up rapidly when running computationally intensive programs. This temperature rise often triggers increased fan speeds and rapid cooling. When power plants are brought online, steam generator tubes experience rapid heating. In both cases, prediction and characterization of heating and cooling rates are important to prevent materials from failing due to overheating and fatigue. Transient heat transfer analyses, as demonstrated in this investigation, are critical for engineering such technologies.
Skip to...
Videos from this collection:

Now Playing
Quenching and Boiling
Mechanical Engineering
7.7K Views

Buoyancy and Drag on Immersed Bodies
Mechanical Engineering
29.9K Views

Stability of Floating Vessels
Mechanical Engineering
22.4K Views

Propulsion and Thrust
Mechanical Engineering
21.6K Views

Piping Networks and Pressure Losses
Mechanical Engineering
58.1K Views

Hydraulic Jumps
Mechanical Engineering
40.9K Views

Heat Exchanger Analysis
Mechanical Engineering
28.0K Views

Introduction to Refrigeration
Mechanical Engineering
24.7K Views

Hot Wire Anemometry
Mechanical Engineering
15.5K Views

Measuring Turbulent Flows
Mechanical Engineering
13.5K Views

Visualization of Flow Past a Bluff Body
Mechanical Engineering
11.8K Views

Jet Impinging on an Inclined Plate
Mechanical Engineering
10.7K Views

Conservation of Energy Approach to System Analysis
Mechanical Engineering
7.4K Views

Mass Conservation and Flow Rate Measurements
Mechanical Engineering
22.6K Views

Determination of Impingement Forces on a Flat Plate with the Control Volume Method
Mechanical Engineering
26.0K Views
Copyright © 2025 MyJoVE Corporation. All rights reserved