Force and Acceleration
Source: Nicholas Timmons, Asantha Cooray, PhD, Department of Physics & Astronomy, School of Physical Sciences, University of California, Irvine, CA
The goal of this experiment is to understand the components of force and their relation to motion through the use of Newton's second law by measuring the acceleration of a glider being acted upon by a force.
Nearly every aspect of motion in everyday life can be described using Isaac Newton's three laws of motion. They describe how objects in motion will tend to stay in motion (the first law), objects will accelerate when acted upon by a net force (the second law), and every force exerted by an object will have an equal and opposite force exerted back onto that object (the third law). Almost all of high school and undergraduate mechanics is based on these simple concepts.
One of the most famous equations in all of physics is Newton's second law:
 . (Equation 1)
. (Equation 1)
It simply states that the force on an object is equal to the mass of the object times its acceleration.
In the experiment to follow, a glider will be connected to a falling weight by a pulley. Because friction caused by the glider sliding along a track would result in an extra force that is difficult to measure, the glider will be on an air track to reduce friction. The air track creates a cushion of air between the glider and track, reducing any friction to approximately zero. The force of the weight will accelerate the glider according to Equation 1.
The force on the weight will be due to gravity and the tension in the string connecting the falling weight to the glider. The tension will oppose the direction of the falling weight and will have the opposite sign as the force of gravity in the equation. Thus, Equation 1 becomes 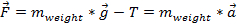 , where T is the tension and
, where T is the tension and  is the acceleration due to gravity (~9.8 m/s2). While the acceleration due to gravity will remain the same, the force can be increased by adding mass.
is the acceleration due to gravity (~9.8 m/s2). While the acceleration due to gravity will remain the same, the force can be increased by adding mass.
As the weight falls, it creates tension in the string connecting the weight to the glider. The pulley changes the direction of the tension force from vertical to horizontal. With nothing else connected, the tension in the string is equal to the force of the falling weight, which applies the same magnitude of force to the glider. Therefore, the force on the glider will be equal to the tension force T;  Because the weight and the glider are connected, their acceleration will be the same for both objects. To calculate the acceleration on the glider due to the pull of the weight, the forces are equated.
Because the weight and the glider are connected, their acceleration will be the same for both objects. To calculate the acceleration on the glider due to the pull of the weight, the forces are equated.
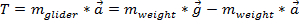 , which can be solved for :
, which can be solved for : 
 . (Equation 2)
. (Equation 2)
To measure the acceleration, a photogate timer is placed 20 cm from the initial position of the glider. The acceleration can be calculated from the measured final velocity and distance traveled using the following equation:
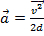 , (Equation 3)
, (Equation 3)
where 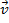 is the final velocity and
is the final velocity and  is the distance traveled. The flag at the top of the glider will pass through the photogate, which will record the amount of time the glider takes to pass through the gate. The flag is 10 cm long, so the velocity of the glider is equal to the length of the flag divided by the time.
is the distance traveled. The flag at the top of the glider will pass through the photogate, which will record the amount of time the glider takes to pass through the gate. The flag is 10 cm long, so the velocity of the glider is equal to the length of the flag divided by the time.
1. Initial setup.
- The air track will have a pulley connected to one end. Tie the string to one end of the glider and run it through the pulley, where it will be connected to the hanging weight.
- Place the glider at the 190-cm mark on the air track. Place the photogate timer at the 100-cm mark. The glider itself has a mass of 200 g. Hold onto the glider so that it does not move and add weights to the hanging end so that the total mass of the weight is equal to 10 g.
- Once the weights are in place, release the glider from rest and record the velocity of the glider. Perform 5 runs and take the average value.
- Calculate the theoretical value for acceleration using Equation 2 and the experimental value from Equation 3. For example, if the glider has mass of 200 g and the hanging weights have a mass 10 g, then the theoretical acceleration, from Equation 2, is
 If the measured velocity is 0.95 m/s, then, using Equation 3, the experimental value for acceleration is
If the measured velocity is 0.95 m/s, then, using Equation 3, the experimental value for acceleration is 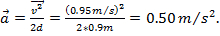
2. Increasing the mass of the glider.
- Add four of the weights to the glider, which will double its mass.
- Release the system from rest and record the velocity of the glider. Perform 5 runs and take the average value. Calculate the theoretical value for acceleration, from Equation 2, and the experimental value, from Equation 3.
3. Increasing the force on the glider.
- Add more mass to the hanging weight so that it has a total mass of 20 g.
- Release the system from rest and record the velocity of the glider. Perform 5 runs and take the average value.
- Calculate the theoretical value for acceleration, from Equation 2, and the experimental value, from Equation 3.
- Add more mass to the hanging weight so that it has a total mass of 50 g.
- Release the system from rest and record the velocity of the glider. Perform 5 runs and take the average value.
- Calculate the theoretical value for acceleration, from Equation 2, and the experimental value, from Equation 3.
  |
  |
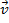 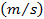 |
 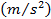 |
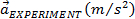 |
% Difference |
| 200 | 10 | 0.93 | 0.47 | 0.43 | 9 |
| 400 | 10 | 0.66 | 0.24 | 0.22 | 9 |
| 200 | 20 | 1.28 | 0.89 | 0.82 | 9 |
| 200 | 50 | 1.96 | 1.69 | 1.92 | 145 |
The results of this experiment confirm the predictions made by Equations 2 and 3. With the increased mass of the glider in step 2, the acceleration was smaller because a larger force would be needed to accelerate the glider to the same velocity as in step 1. In step 3, the increased mass of the hanging weight did indeed increase the force on the glider and thus the acceleration. The acceleration increased with the increased mass, as predicted.
Friction was nearly zero thanks to the air cushion between the glider and the track. The pocket of air is not perfect, however, and the air from the track might push the glider in a specific direction. This can be tested by allowing the glider to sit on the air track, with no force applied to it. If the glider moves in either direction, there might be some force on the glider from the track.
Newton's second law is fundamentally linked to the motion people experience every day. Without any force, an object will not accelerate and will remain at rest or will continue to move at a constant rate. Therefore, if someone wants to move something, such as when hitting a baseball a certain distance, sufficient force must be applied. The force can be calculated with an equation as simple as 
Just as it takes a certain force to accelerate an object, it takes the same amount of force to bring the velocity of an object down to zero. By looking at  , it is clear that an abject with a lot of mass is much harder to stop than an object with a smaller mass. It is easier to stop a bike than a train! The faster something is going, the more acceleration is required to bring it to a stop, so it takes much more force to stop a bullet than a basketball.
, it is clear that an abject with a lot of mass is much harder to stop than an object with a smaller mass. It is easier to stop a bike than a train! The faster something is going, the more acceleration is required to bring it to a stop, so it takes much more force to stop a bullet than a basketball.
Newton's second law becomes a bit more complicated when the components of force change with time. For an object that is experiencing some kind of drag force, such as air resistance, its acceleration can change with time. A rocket is an example of an object that has a mass that changes with time. As the rocket burns fuel, its mass gets smaller, and it actually requires less force to accelerate as time passes.
In this experiment, the components of force were examined. Newton's second law states that force is equal to the mass of an object multiplied by the acceleration. By adjusting the mass of the glider, the acceleration of the glider was reduced. With increased force on the glider, the acceleration was increased, confirming Newton's second law. The results of this experiment should be accurate, as long as there are no other forces acting on the glider. This is why friction was reduced in this experiment using an air track.
Skip to...
Videos from this collection:

Now Playing
Force and Acceleration
Physics I
79.1K Views

Newton's Laws of Motion
Physics I
75.7K Views

Vectors in Multiple Directions
Physics I
182.3K Views

Kinematics and Projectile Motion
Physics I
72.6K Views

Newton's Law of Universal Gravitation
Physics I
190.8K Views

Conservation of Momentum
Physics I
43.3K Views

Friction
Physics I
52.9K Views

Hooke's Law and Simple Harmonic Motion
Physics I
61.3K Views

Equilibrium and Free-body Diagrams
Physics I
37.3K Views

Torque
Physics I
24.3K Views

Rotational Inertia
Physics I
43.5K Views

Angular Momentum
Physics I
36.2K Views

Energy and Work
Physics I
49.7K Views

Enthalpy
Physics I
60.4K Views

Entropy
Physics I
17.6K Views
Copyright © 2025 MyJoVE Corporation. All rights reserved