Angular Momentum
Overview
Source: Nicholas Timmons, Asantha Cooray, PhD, Department of Physics & Astronomy, School of Physical Sciences, University of California, Irvine, CA
Angular momentum is defined as the product of the moment of inertia and the angular velocity of the object. Like its linear analog, angular momentum is conserved, meaning that the total angular momentum of a system will not change if there are no external torques on the system. A torque is the rotational equivalent of a force. Because it is a conserved, angular momentum is an important quantity in physics.
The goal of this experiment is to measure the angular momentum of a rotating rod and to use the conservation of angular momentum to explain two rotational demonstrations.
Principles
Angular momentum can be written as:
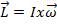 , (Equation 1)
, (Equation 1)
where 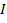 is the moment of inertia and
is the moment of inertia and  is the angular velocity. The moment of inertia is the rotational analog of mass for linear motion. It is related to the mass distribution of a rotating object and the axis of rotation. The larger the moment of inertia, the more torque is needed to cause an angular acceleration on an object. The right-hand rule can be used to determine the direction of angular momentum. When the fingers of the right hand curl in the direction of rotation, the extended thumb points in the direction of angular momentum.
is the angular velocity. The moment of inertia is the rotational analog of mass for linear motion. It is related to the mass distribution of a rotating object and the axis of rotation. The larger the moment of inertia, the more torque is needed to cause an angular acceleration on an object. The right-hand rule can be used to determine the direction of angular momentum. When the fingers of the right hand curl in the direction of rotation, the extended thumb points in the direction of angular momentum.
A torque is defined as the product of a force applied at some distance from an axis of rotation:
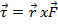 , (Equation 2)
, (Equation 2)
where 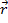 is the distance to the axis of rotation and
is the distance to the axis of rotation and 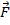 is the force applied. If a torque acts on an object, the angular velocity of that object will change, along with its angular momentum. If the sum of the torques on an object is equal to zero, then the total angular momentum will be conserved and will have the same final value as it did initially.
is the force applied. If a torque acts on an object, the angular velocity of that object will change, along with its angular momentum. If the sum of the torques on an object is equal to zero, then the total angular momentum will be conserved and will have the same final value as it did initially.
A fun example of the conservation of angular momentum can be demonstrated with a bike wheel and a rotating chair. The wheel and the person in the chair constitute a system with some angular momentum. If the person applies a torque to spin the wheel, with the axis pointing vertically, the system will have gained angular momentum. If the person then flips the spinning wheel over, she will begin to spin in her chair in the opposite direction of the spinning wheel. Here, the system had angular momentum, with its direction determined by the right-hand rule. When the wheel was flipped, the angular momentum of the system changed direction. Because of conservation, the chair began to rotate in the opposite direction so that the total angular momentum of the system was equal to that of the system before the wheel was flipped.
Another demonstration of the conservation of angular momentum can be done with a spinning chair and two weights. If the weights are held out at arm's length while the chair is spinning and then are brought in close to the chest, there will be an increase in angular velocity. This happens because bringing the weights nearer to the axis of rotation decreases the moment of inertia of the system. If there is no more force acting to spin the chair, then the torque on the system is zero. The angular momentum must remain constant, as there are no torques, and the only way for that to happen is for the angular speed to increase.
In this experiment, a rotating rod is connected to a falling weight. The falling weight will provide a torque on the rod, and the angular momentum will be measured at two points: first when the weight has fallen halfway and then again once the weight reaches the end of the string. See Figure 1 for an image of the experimental setup.
The moment of inertia of a spinning rod is 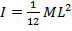 , where
, where 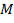 is the mass of the rod and
is the mass of the rod and 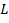 is the length. These quantities can be measured before the experiment takes place. To find the angular velocity
is the length. These quantities can be measured before the experiment takes place. To find the angular velocity  , the rotational kinematic equations will be used:
, the rotational kinematic equations will be used:
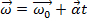 . (Equation 3)
. (Equation 3)
Equation 3 states that the final angular velocity  is equal to the initial angular velocity
is equal to the initial angular velocity  plus the angular acceleration
plus the angular acceleration 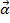 , multiplied by time. Because the rod will begin at rest,
, multiplied by time. Because the rod will begin at rest,  will be equal to zero. The angular acceleration
will be equal to zero. The angular acceleration 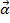 is defined by
is defined by 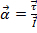 , where
, where 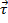 is the torque and
is the torque and 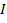 is the moment of inertia. The torque is the cross product of the distance from the axis of rotation to the force, and the force of the weight causing a tension in the string, which causes the rod to rotate:
is the moment of inertia. The torque is the cross product of the distance from the axis of rotation to the force, and the force of the weight causing a tension in the string, which causes the rod to rotate: 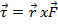 . That force acting on the pulley is equal to the force on the weight:
. That force acting on the pulley is equal to the force on the weight: 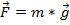 , where
, where 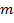 is the mass and
is the mass and 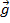 is the acceleration due to gravity. The radius
is the acceleration due to gravity. The radius 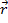 of the torque will be the distance from the wound string to the axis of rotation.
of the torque will be the distance from the wound string to the axis of rotation.

Figure 1. Experimental setup. Inset: 1) large ring stand, 2) extender, 3) rotating assembly, 4) weight, and 5) torque bar.
Procedure
1. Test the theory of the conservation of angular momentum with the bike wheel.
- While sitting in a chair that can freely rotate, start spinning the bike wheel and then hold it by the handles so that its direction of angular momentum is vertical.
- While holding the wheel by the two handles, flip the wheel over so that its angular momentum points in the opposite direction. Notice how the chair will begin to rotate.
2. Test the theory of the conservation of angular momentum with two weights.
- While sitting in a chair that can freely rotate, hold two weights out at arm's length.
- Have a partner get the chair spinning and then bring the weights in close to the chest. Notice the increased speed of rotation of the chair.
3. Measure the change of angular momentum in the spinning rod.
- Measure the length of the rod and its mass. Using a meter stick, measure the halfway point of the falling weight and mark the vertical beam with tape in order to have a reference. Calculate the moment of inertia of the rod.
- Add 200 g to the end of the string and wind it up to the top. Take notice of where the halfway point of the string is located.
- Release the weight and measure the amount of time it takes to get to the halfway mark and then again to the bottom. Do this three times and take the average values. Calculate the angular momentum at both points.
- Increase the weight at the end of the string to 500 g and repeat step 3.3.
- Increase the weight to 1,000 g and repeat step 3.3.
Results
| Mass (g) |
Angular momentum at halfway (kg m2)/s |
Angular momentum at bottom (kg m2)/s |
Difference (kg m2)/s |
| 200 | 0.41 | 0.58 | 0.17 |
| 500 | 0.66 | 0.91 | 0.25 |
| 1,000 | 0.93 | 1.32 | 0.39 |
In step one, the theory of conservation of angular momentum was confirmed, as the chair began to rotate when the wheel was flipped over. In step two, the theory of conservation of angular momentum was again confirmed, as the chair began to spin faster when the weights were brought in and the moment of inertia of the system was reduced. In step three of the lab, the increased torque on the spinning rod increased the angular momentum. With all the other quantities being constant, the angular momentum increased linearly with time.
Application and Summary
Just like in the spinning chair portion of the lab, changing the moment of inertia of an object can increase or decrease the angular velocity of that object. Figure skaters take advantage of this and will sometimes begin spinning with their arms outstretched and then bring their arms in close to their bodies, which will make them spin much faster.
Why is it easier to balance on a bike when it is in motion? The answer is angular momentum. When the wheels are not spinning, it is easy for the bike to fall over. Once the wheels are in motion, they will have some amount of angular momentum. The larger the angular momentum, the more torque is required to change it, so it is harder to tip the bike over.
If a quarterback playing football throws without putting any spin on the ball, its flight will be wobbly and might miss its target. To prevent this, quarterbacks use their fingers to get the football spinning when they throw it. When the ball rotates as it flies through the air, it has angular momentum, which requires torque to change the direction of the angular momentum. The ball will not wobble or turn over in the air.
In this experiment, the concept of conservation of momentum was tested in two demonstrations. In one, the direction of angular momentum was conserved, and in the other, the magnitude was conserved. In the last part of the experiment, the effect of a torque on angular momentum was measured.
Skip to...
Videos from this collection:

Now Playing
Angular Momentum
Physics I
36.2K Views

Newton's Laws of Motion
Physics I
75.7K Views

Force and Acceleration
Physics I
79.1K Views

Vectors in Multiple Directions
Physics I
182.3K Views

Kinematics and Projectile Motion
Physics I
72.6K Views

Newton's Law of Universal Gravitation
Physics I
190.8K Views

Conservation of Momentum
Physics I
43.3K Views

Friction
Physics I
52.9K Views

Hooke's Law and Simple Harmonic Motion
Physics I
61.3K Views

Equilibrium and Free-body Diagrams
Physics I
37.3K Views

Torque
Physics I
24.3K Views

Rotational Inertia
Physics I
43.5K Views

Energy and Work
Physics I
49.7K Views

Enthalpy
Physics I
60.4K Views

Entropy
Physics I
17.6K Views
Copyright © 2025 MyJoVE Corporation. All rights reserved