Entropy is a "state property," which is a quantity that depends only upon the current state of the system. Quantities that are state properties do not depend on the path by which the system arrived at its present state. Therefore, the most useful way to quantify a state property is to measure its change.

The change in entropy S is defined as:

ΔS = Q / T, (Equation 1)

where Q is the heat supplied to the system and T is the temperature of the system. In the context of thermodynamics, heat, like work, is defined as a transfer of energy. Heat is energy transferred from one object to another because of a difference in temperature. Consider a bath of ice and water at 0 °C. If one supplies heat to the ice/water bath, some of the ice will melt, and the number of states available to the water molecules will increase by a large amount, proportional to the amount of heat that was added to the system. The entropy will then increase proportionally to this amount. The relationship between two objects at different temperatures was first described by Newton.

Newton's law of cooling states that the rate of change of the temperature of some object is proportional to the difference between its own temperature and the temperature of its surroundings. For an object at temperature T placed in a closed system at temperature T_f, this change in temperature as a function of time t is described by the differential equation:

dT/dt = -k(T - T_f ), (Equation 2)

where k is a constant that depends upon the characteristics of the object and its surroundings. Equation 1 is equivalently written as:

-k dt = dT / (T - T_f ). (Equation 3)

Integrating both sides gives:

-k t = log(T - T_f ) + log C. (Equation 4)

Applying the exponential function to both sides of the equation and then rearranging gives:

T - T_f = C e^-kt . (Equation 5)

If the object in question is at an initial temperature T_i at time t = 0:

T_i- T_f = C. (Equation 6)

It follows that the temperature as a function of time is:

T(t) =T_f + (T_i- T_f ) e^-kt .(Equation 7)

Therefore, when a hot object is placed in a cooler closed system, its temperature will decrease at an exponential rate. In this closed system, the heat from the hot object Q will increase the temperature of the cooler surroundings and thus increase the number of available states. Thus, the change in entropy, ΔS, is positive and nonzero.

Representative results for 680 mL of water are shown in Table 1. The cooling constant k was found using the data points in the table and solving Equation 7. After 35 min, T(35) = 50.6. The initial temperature was 100 °C, and data collection ceased at 28.5 °C. Using these variables gives the following equation to obtain k:

50.6 = 28.5 + (100 - 28.5) e^{-k 35}. (Equation 8)

Solving for k gives a value k = 0.034. The curve with this cooling constant is shown as a dashed gray line in Figure 1, along with the data points from the experiment. The functional form of Equation 6 matches the experimental results very closely.

As the water cools, the entropy decreases, since the number of states available to the water molecules decreases. The entropy of the ambient air in the room increases because the water beaker transfers heat to the air molecules surrounding it; the overall entropy of the water + air system increases. The number of states that the now-hotter air molecules can occupy is much higher than before the hot water was introduced to the room.

In differential form, the heat dQ added to or removed from the water can be calculated using the relationship between mass, specific heat c, and temperature change:

dQ = mc dT, (Equation 9)

where c is known to be 4.18 J/(gK) for water. The change in entropy of the water is then:

ΔS_water =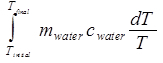

= m_water c_water ln(T_final / T_initial). (Equation 10)

Using the conversion to Kelvin as K = °C + 273.15, the change in the entropy of the water is calculated as:

ΔS_water = 680 g * 4.18 J/(g K) * ln[(28.5 + 273.15)/(100 + 273.15)]

= -604 J/K.

The ambient air temperature is constant at 20.4 °C, so this is an isothermal process. The entropy change of the air is then:

ΔS_air = ,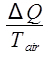

where Q is the heat released by the water, which is given by Equation 9. The change in entropy of the air is then calculated as:

ΔS_air =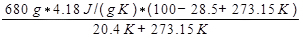

= 3337 J/K.

The total change in the entropy of the water + air system, ΔS_tot, is the sum of the individual changes in entropy of the water and ambient air:

ΔS_tot = ΔS_water +ΔS_air (Equation 11)

= -604 J/k + 3337 J/K

= 2733 J/K.

Table 1. Temperatures recorded during the experiment.

Time (min s)	Water Temperature (°C)
0 0	99.6
1 10	97.1
1 50	94.2
2 30	91.8
3 22	89
4 05	87.2
5 08	82.7
6 05	82.4
8 25	78
9 15	76.5
10 15	74.6
11 38	72.7
12 58	70.7
13 58	69.2
15 15	67.7
16 55	65.8
18 38	64
20 25	62.3
24 02	58.8
25 45	57.3
34 45	50.6
40 50	47.4
44 30	45.9
49 59	43.6
53 42	42.4
60 01	40.2
64 20	39.5
76 37	37
103 50	32.1
116 41	30.3
122 46	29.6
134 11	28.5

Figure 1. Plot of temperature versus time. The blue dots indicate the experimental data, and the dashed line represents theoretical data based on Newton's law of cooling.

A pair of headphones kept in a bag always tends to become knotted-this is an increase in entropy caused by carrying the bag around. It is necessary to do work on the headphones to un-knot them and decrease the entropy (this can be thought of as a "reversible process"). The most efficient heat engine cycle allowed by physical laws is the Carnot cycle. The second law states that not all heat supplied to a heat engine can be used to do work. The Carnot efficiency sets the limiting value on the fraction of heat that can be used. The cycle consists of two isothermal processes followed by two adiabatic processes. A refrigerator, which is essentially just a heat pump, is also a classic example of the second law. Refrigerators move heat from one location at a lower temperature (the "source") to another location at a higher temperature (the "heat sink") using mechanical work. According to the second law, heat cannot spontaneously flow from a colder location to a hotter one; thus, work (energy) is required for refrigeration.

Newton's law of cooling was demonstrated by a beaker full of water at 100 °C cooling down to room temperature, which led to an increase in the entropy of the water-air system. By measuring the temperature of the water as a function of time over a period of 135 min, it was possible to confirm that the cooling of the water was exponential in form. The cooling constant of the water sample was found by solving the cooling equation using collected data.