Force et accélération

Source : Nicholas Timmons, Antonella Cooray, Ph.d., département de physique & astronomie, école de Sciences physique, University of California, Irvine, CA

L’objectif de cette étude est de comprendre les composantes de la force et de leur relation avec le mouvement grâce à l’utilisation de la seconde loi de Newton en mesurant l’accélération d’un planeur étant suivie par une force.

Presque tous les aspects du mouvement dans la vie quotidienne peuvent être décrits en utilisant les trois lois de Isaac Newton du mouvement. Ils décrivent comment les objets en mouvement aura tendance à rester en mouvement (la première loi), objets vont accélérer lorsque suivies par une force nette (la deuxième loi) et toutes les forces exercées par un objet auront un égal et opposé force arrière exercée sur cet objet (la troisième loi). La quasi-totalité des études secondaires et premier cycle mécanique repose sur ces concepts simples.

L’un des plus célèbres équations dans l’ensemble de la physique est la seconde loi de Newton :

. (Équation 1)

Il indique simplement que la force sur un objet est égale à la masse de l’objet fois son accélération.

Dans l’expérience à suivre, un planeur sera relié à une masse tombante par une poulie. Parce que la friction causée par le planeur en faisant glisser le long d’une piste se traduirait par une force supplémentaire qui est difficile à mesurer, le planeur sera mis sur une voie d’air pour réduire la friction. La voie d’air crée un coussin d’air entre le planeur et le rail, réduisant toute friction à environ zéro. La force du poids va accélérer le planeur selon l’équation 1.

La force du poids sera due à la gravité et la tension de la chaîne reliant la masse tombante à la voile. La tension s’opposera à la direction de la masse tombante et aura le signe opposé comme la force de gravité dans l’équation. Ainsi, l’équation 1 devient 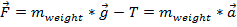, où T est la tension et est l’accélération due à la pesanteur (~9.8 m/s²). Alors que l’accélération due à la pesanteur restera la même, la force peut être augmentée en ajoutant la masse.

Le poids est tombée, elle crée des tensions dans la chaîne reliant le poids de l’aile. La poulie change la direction de la force de tension de la verticale à l’horizontale. Avec rien d’autre connecté, la tension de la chaîne est égale à la force de la masse tombante, qui s’applique de la même intensité de force à l’aile. Par conséquent, la force sur le planeur sera égale à la force de tension T ;  Parce que le poids et le parapente sont connectés, leur accélération seront les mêmes pour les deux objets. Pour calculer l’accélération sur le planeur dû à la traction du poids, les forces sont égalisées.

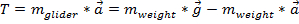, qui peut être résolu pour :

. (Équation 2)

Pour mesurer l’accélération, une minuterie de photogate se trouve à 20 cm de la position initiale du planeur. L’accélération peut être calculée à partir la vitesse finale mesurée et la distance parcourue à l’aide de l’équation suivante :

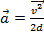, (Équation 3)

où 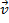est la vitesse finale et est la distance parcourue. Le drapeau en haut de l’aile passera par la photogate, qui va enregistrer la quantité de temps que le planeur faut passer par la porte. Le drapeau est de 10 cm de long, donc la vitesse du planeur est égale à la longueur du drapeau divisé par le temps.

1. première installation.

1. La voie d’air aura une poulie reliée à une extrémité. Attacher la chaîne à une extrémité de l’aile et l’exécuter dans la poulie, où elle sera connectée à la masse suspendue.
2. Placer l’aile à la marque de 190 cm sur la voie de l’air. Placer le minuteur de photogate à la marque de 100 cm. Le planeur lui-même a une masse de 200 g. agripper le planeur afin qu’il ne pas se déplacer et ajouter des poids à la fin de la suspension, afin que le poids de la masse total est égal à 10 g.
3. Une fois que les poids sont en place, libérer la voile reste et d’enregistrer la vitesse du planeur. Effectuer 5 séries et prendre la valeur moyenne.
4. Calculer la valeur théorique d’accélération à l’aide de l’équation 2 et la valeur expérimentale de l’équation 3. Par exemple, si le planeur a masse de 200 g et les poids suspendus ont une masse 10 g, puis l’accélération théorique, de l’équation 2, est si la vitesse mesurée est de 0,95 m/s, puis, à l’aide de l’équation 3, la valeur expérimentale pour l’accélération est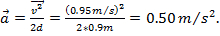

2. augmentation de la masse du chariot.

1. Ajouter quatre des poids de l’aile, ce qui va doubler sa masse.
2. Libérer le système reste et d’enregistrer la vitesse du planeur. Effectuer 5 séries et prendre la valeur moyenne. Calculer la valeur théorique pour l’accélération, de l’équation 2et la valeur expérimentale, de l’équation 3.

3. augmenter la force sur l’aile.

1. Ajouter plus de masse à la masse suspendue afin qu’il ait une masse totale de 20 g.
2. Libérer le système reste et d’enregistrer la vitesse du planeur. Effectuer 5 séries et prendre la valeur moyenne.
3. Calculer la valeur théorique pour l’accélération, de l’équation 2et la valeur expérimentale, de l’équation 3.
4. Ajouter plus de masse à la masse suspendue afin qu’il ait une masse totale de 50 g.
5. Libérer le système reste et d’enregistrer la vitesse du planeur. Effectuer 5 séries et prendre la valeur moyenne.
6. Calculer la valeur théorique pour l’accélération, de l’équation 2et la valeur expérimentale, de l’équation 3.

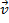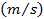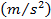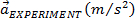					Pourcentage de différence
200	10	0,93	0,47	0,43	9
400	10	0,66	0,24	0,22	9
200	20	1.28	0,89	0,82	9
200	50	1,96	1.69	1,92	145

Les résultats de cette étude confirment les prédictions faites par les équations 2 et 3. Avec l’augmentation de la masse de l’aile à l’étape 2, l’accélération était plus petite, car il faudrait une force plus importante pour accélérer le planeur à la même vitesse qu’à l’étape 1. À l’étape 3, l’augmentation de la masse du poids suspendu a fait en effet augmenter la force sur l’aile et donc l’accélération. L’accélération augmente avec l’augmentation de la masse, comme l’avait prédit.

Friction a été presque nul grâce au coussin d’air entre l’aile et la piste. La poche d’air n’est pas parfaite, cependant, et l’air de la piste pourrait pousser le planeur dans une direction précise. Cela peut être testé en permettant au planeur s’asseoir sur la voie aérienne, avec aucune force exercée sur. Si la voile se déplace dans les deux sens, il pourrait y avoir une certaine force sur l’aile de la piste.

Deuxième loi de Newton est fondamentalement liée à l’expérience de personnes du mouvement tous les jours. Sans aucune force, un objet n’accélérera pas et restera au repos ou continue à se déplacer à une vitesse constante. Par conséquent, si quelqu'un veut passer quelque chose, comme en frappant une balle de baseball une certaine distance, une force suffisante doit être appliquée. La force peut être calculée avec une équation simple comme

Juste comme il faut une certaine force pour accélérer un objet, il faut la même quantité de force pour ramener la vitesse d’un objet à zéro. En regardant , il est clair qu’une abjecte avec beaucoup de masse est beaucoup plus difficile d’arrêter qu’un objet ayant une masse plus petite. Il est plus facile d’arrêter un vélo qu’un train ! Plus vite quelque chose se passe, l’accélération plus est nécessaire pour amener à un arrêt, il prend beaucoup plus de force pour arrêter une balle qu’un ballon de basket.

Deuxième loi de Newton devient un peu plus compliquée lorsque les composantes de force évoluent avec le temps. Pour un objet qui connaît certains type de glisser force, comme la résistance de l’air, son accélération peut changer avec le temps. Une fusée est un exemple d’un objet qui a une masse qui change avec le temps. Comme la fusée brûle le carburant, sa masse devient plus petite, et il faut effectivement moins de force pour accélérer au fil des ans.

Dans cette expérience, les composantes de force ont été examinés. Deuxième loi de Newton stipule que la force est égale à la masse d’un objet multipliée par l’accélération. En ajustant la masse du chariot, l’accélération du planeur a été réduite. Avec une force accrue sur le planeur, l’accélération a été augmentée, confirmant la seconde loi de Newton. Les résultats de cette expérience doivent être précis, tant qu’il n’y a pas d’autres forces agissant sur le planeur. C’est pourquoi le frottement a été réduite dans cette expérience en utilisant une voie d’air.